ELEMENTARY STATISTICS Section 3 3 Addition Rule MARIO




















- Slides: 22

ELEMENTARY STATISTICS Section 3 -3 Addition Rule MARIO F. TRIOLA EIGHTH Chapter 3. Section 3 -3. Triola, Elementary Statistics, Eighth Edition. Copyright 2001. Addison Wesley Longman EDITION 1

Definition v Compound Event Any event combining 2 or more simple events v Notation P(A or B) = P (event A occurs or event B occurs or they both occur) Chapter 3. Section 3 -3. Triola, Elementary Statistics, Eighth Edition. Copyright 2001. Addison Wesley Longman 2

Compound Event General Rule When finding the probability that event A occurs or event B occurs, find the total number of ways A can occur and the number of ways B can occur, but find the total in such a way that no outcome is counted more than once. Chapter 3. Section 3 -3. Triola, Elementary Statistics, Eighth Edition. Copyright 2001. Addison Wesley Longman 3

Compound Event Formal Addition Rule P(A or B) = P(A) + P(B) - P(A and B) where P(A and B) denotes the probability that A and B both occur at the same time. Chapter 3. Section 3 -3. Triola, Elementary Statistics, Eighth Edition. Copyright 2001. Addison Wesley Longman 4

Compound Event Formal Addition Rule P(A or B) = P(A) + P(B) - P(A and B) where P(A and B) denotes the probability that A and B both occur at the same time. Intuitive Addition Rule To find P(A or B), find the sum of the number of ways event A can occur and the number of ways event B can occur, adding in such a way that every outcome is counted only once. P(A or B) is equal to that sum, divided by the total number of outcomes. Chapter 3. Section 3 -3. Triola, Elementary Statistics, Eighth Edition. Copyright 2001. Addison Wesley Longman 5

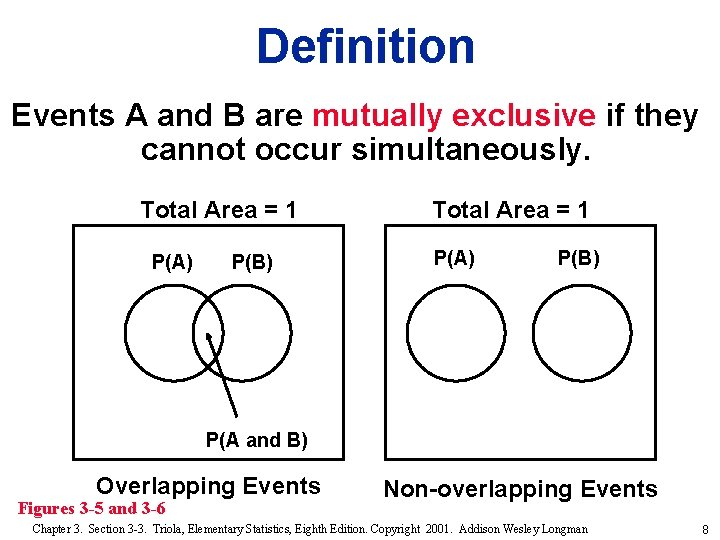
Definition Events A and B are mutually exclusive if they cannot occur simultaneously. Chapter 3. Section 3 -3. Triola, Elementary Statistics, Eighth Edition. Copyright 2001. Addison Wesley Longman 6

Definition Events A and B are mutually exclusive if they cannot occur simultaneously. Total Area = 1 P(A) P(B) P(A and B) Overlapping Events Figures 3 -5 Chapter 3. Section 3 -3. Triola, Elementary Statistics, Eighth Edition. Copyright 2001. Addison Wesley Longman 7

Definition Events A and B are mutually exclusive if they cannot occur simultaneously. Total Area = 1 P(A) P(B) P(A and B) Overlapping Events Figures 3 -5 and 3 -6 Non-overlapping Events Chapter 3. Section 3 -3. Triola, Elementary Statistics, Eighth Edition. Copyright 2001. Addison Wesley Longman 8

Figure 3 -7 Applying the Addition Rule P(A or B) Addition Rule Are A and B mutually exclusive ? Yes P(A or B) = P(A) + P(B) No P(A or B) = P(A)+ P(B) - P(A and B) Chapter 3. Section 3 -3. Triola, Elementary Statistics, Eighth Edition. Copyright 2001. Addison Wesley Longman 9

Contingency Table Survived Died Total Men 332 1360 1692 Women 318 104 422 Boys 29 35 64 Girls 27 18 45 Totals 706 1517 2223 Find the probability of randomly selecting a man or a boy. Chapter 3. Section 3 -3. Triola, Elementary Statistics, Eighth Edition. Copyright 2001. Addison Wesley Longman 10

Contingency Table Survived Died Total Men 332 1360 1692 Women 318 104 422 Boys 29 35 64 Girls 27 18 45 Totals 706 1517 2223 Find the probability of randomly selecting a man or a boy. Chapter 3. Section 3 -3. Triola, Elementary Statistics, Eighth Edition. Copyright 2001. Addison Wesley Longman 11

Contingency Table Survived Died Total Men 332 1360 1692 Women 318 104 422 Boys 29 35 64 Girls 27 18 45 Totals 706 1517 2223 Find the probability of randomly selecting a man or a boy. P(man or boy) = 1692 + 64 = 1756 = 0. 790 2223 Chapter 3. Section 3 -3. Triola, Elementary Statistics, Eighth Edition. Copyright 2001. Addison Wesley Longman 12

Contingency Table Survived Died Total Men 332 1360 1692 Women Boys Girls Totals 318 29 27 706 104 35 18 1517 422 64 45 2223 Find the probability of randomly selecting a man or a boy. P(man or boy) = 1692 + 64 = 1756 = 0. 790 2223 * Mutually Exclusive * Chapter 3. Section 3 -3. Triola, Elementary Statistics, Eighth Edition. Copyright 2001. Addison Wesley Longman 13

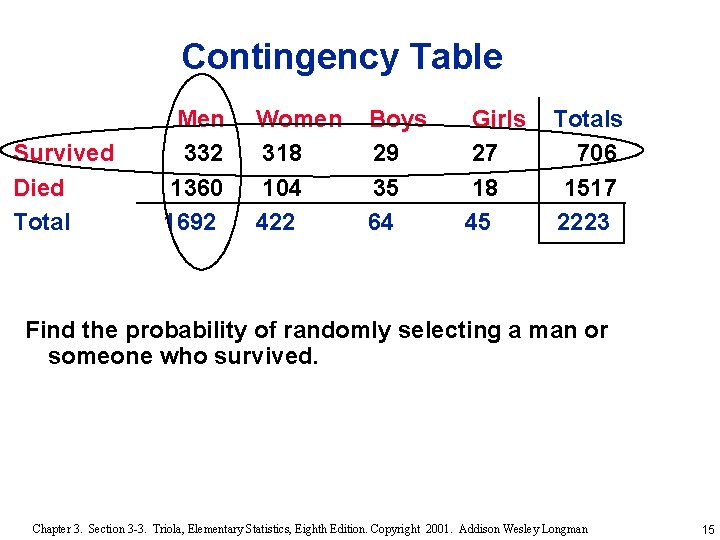
Contingency Table Survived Died Total Men 332 1360 1692 Women 318 104 422 Boys 29 35 64 Girls 27 18 45 Totals 706 1517 2223 Find the probability of randomly selecting a man or someone who survived. Chapter 3. Section 3 -3. Triola, Elementary Statistics, Eighth Edition. Copyright 2001. Addison Wesley Longman 14

Contingency Table Survived Died Total Men 332 1360 1692 Women 318 104 422 Boys 29 35 64 Girls 27 18 45 Totals 706 1517 2223 Find the probability of randomly selecting a man or someone who survived. Chapter 3. Section 3 -3. Triola, Elementary Statistics, Eighth Edition. Copyright 2001. Addison Wesley Longman 15

Contingency Table Survived Died Total Men 332 1360 1692 Women 318 104 422 Boys 29 35 64 Girls 27 18 45 Totals 706 1517 2223 Find the probability of randomly selecting a man or someone who survived. P(man or survivor) = 1692 + 706 - 332 = 2066 2223 = 0. 929 Chapter 3. Section 3 -3. Triola, Elementary Statistics, Eighth Edition. Copyright 2001. Addison Wesley Longman 16

Contingency Table Survived Died Total Men 332 1360 1692 Women 318 104 422 Boys 29 35 64 Girls 27 18 45 Totals 706 1517 2223 Find the probability of randomly selecting a man or someone who survived. P(man or survivor) = 1692 + 706 - 332 = 2066 2223 = 0. 929 * NOT Mutually Exclusive * Chapter 3. Section 3 -3. Triola, Elementary Statistics, Eighth Edition. Copyright 2001. Addison Wesley Longman 17

Complementary Events P(A) and P(A) are mutually exclusive All simple events are either in A or A. P(A) + P(A) = 1 Chapter 3. Section 3 -3. Triola, Elementary Statistics, Eighth Edition. Copyright 2001. Addison Wesley Longman 18

Rules of Complementary Events P(A) + P(A) = 1 - P(A) Chapter 3. Section 3 -3. Triola, Elementary Statistics, Eighth Edition. Copyright 2001. Addison Wesley Longman 19

Figure 3 -8 Venn Diagram for the Complement of Event A Total Area = 1 P (A) = 1 - P (A) Chapter 3. Section 3 -3. Triola, Elementary Statistics, Eighth Edition. Copyright 2001. Addison Wesley Longman 20

Examples 1) A restaurant has 3 pieces of apple pie, 5 pieces of cherry and 4 pieces of pumpkin pie in its dessert case. If a customer selects a piece of pie what is the probability that it is cherry or pumpkin? Events are mutually exclusive P(Cherry or Pumpkin) = P(Cherry) + P(Pumpkin) = 5/12 + 4/12 = 9/12 = 3/4. Chapter 3. Section 3 -3. Triola, Elementary Statistics, Eighth Edition. Copyright 2001. Addison Wesley Longman 21

Examples 1) A single card is selected from a standard deck of cards. What is the probability that it is a king or club? Events are not mutually exclusive P(King or Club) = P(King) + P(Club) – P(King and Club) = 4/52 + 13/52 - 1/52 = 16/52 = 4/13. Chapter 3. Section 3 -3. Triola, Elementary Statistics, Eighth Edition. Copyright 2001. Addison Wesley Longman 22