ELEMENTARY STATISTICS Chapter 7 Normal Distributions Finding Probabilities

ELEMENTARY STATISTICS Chapter 7 Normal Distributions: Finding Probabilities C. M. Pascual 1

Properties of the Normal Distribution 1. The normal distribution curve is bell-shaped; 2. The mean, median, and mode are equal and located at the center of the distribution; 3. The normal distribution curve is unimodal; 4. The curve is symmetrical about the mean; 5. The curve is continuous; 6. The curve never touches the x-axis; 7. The total area under the normal distribution curve is equal to 1 or 100%. C. M. Pascual 2

Other Normal Distributions If 0 or 1 (or both), we will convert values to standard scores using Formula 5 -2, then procedures for working with all normal distributions are the same as those for the standard normal distribution. C. M. Pascual 3

Other Normal Distributions If 0 or 1 (or both), we will convert values to standard scores using Formula 5 -2, then procedures for working with all normal distributions are the same as those for the standard normal distribution. Formula 7 -2 C. M. Pascual z= x-µ 4
Converting to Standard Normal Distribution P (a) x Figure 7 -13 C. M. Pascual 5
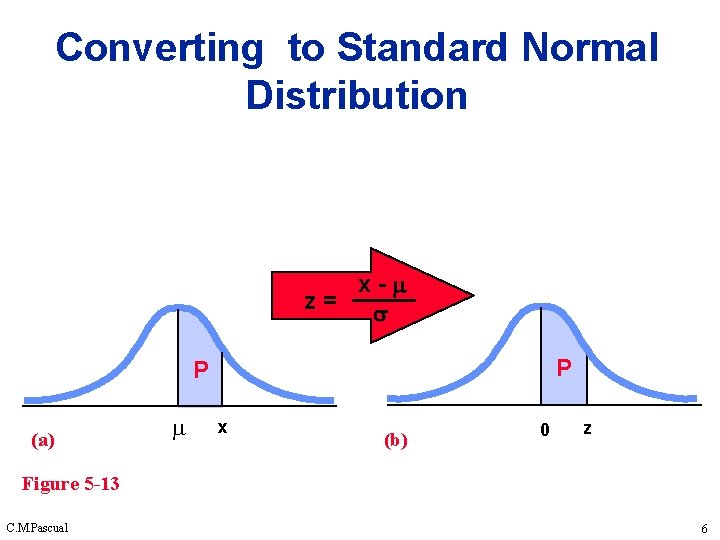
Converting to Standard Normal Distribution x- z= P P (a) x (b) 0 z Figure 5 -13 C. M. Pascual 6
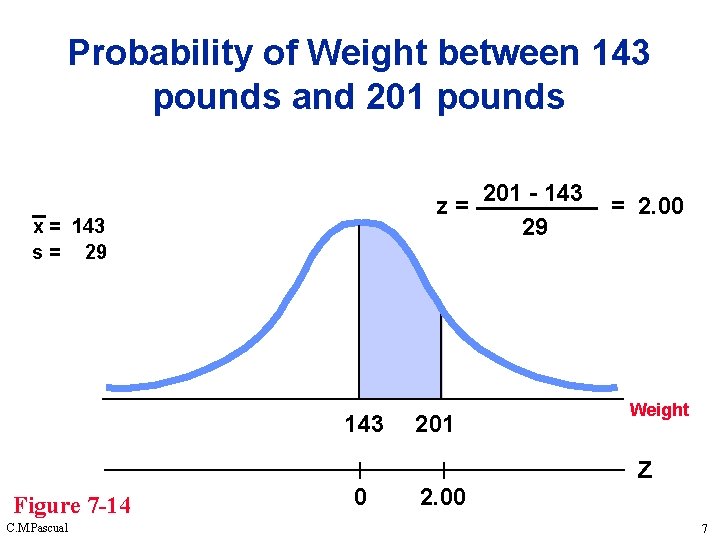
Probability of Weight between 143 pounds and 201 pounds z= x = 143 s = 29 143 Figure 7 -14 C. M. Pascual 0 201 2. 00 201 - 143 29 = 2. 00 Weight z 7
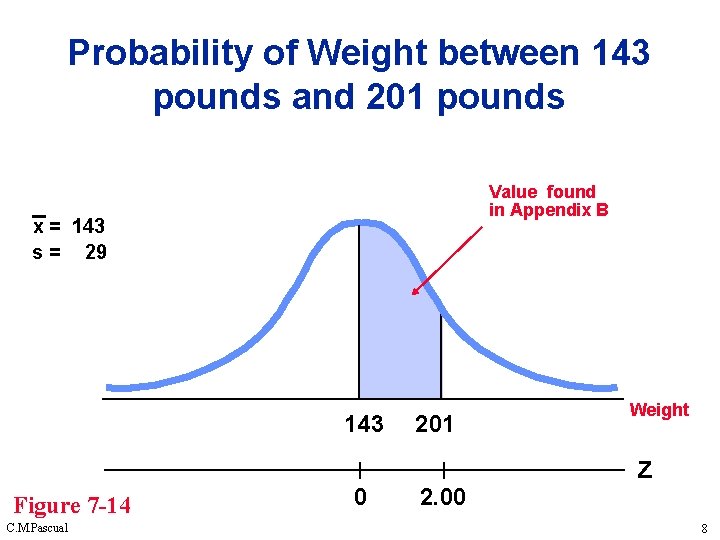
Probability of Weight between 143 pounds and 201 pounds Value found in Appendix B x = 143 s = 29 143 Figure 7 -14 C. M. Pascual 0 201 2. 00 Weight z 8
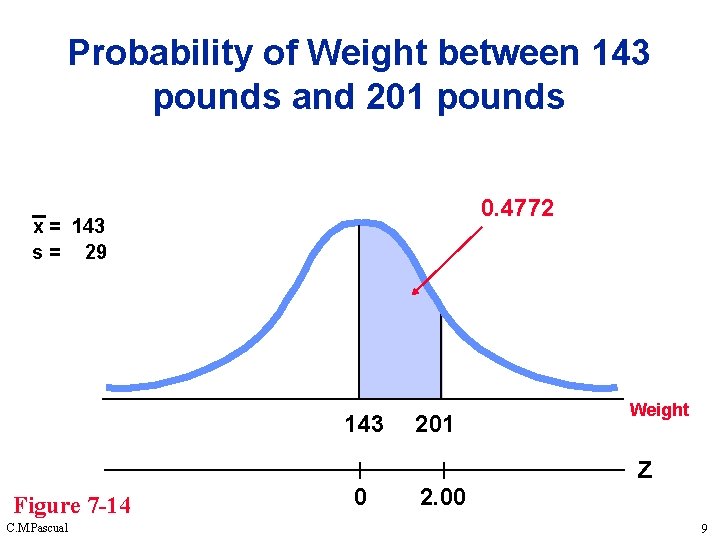
Probability of Weight between 143 pounds and 201 pounds 0. 4772 x = 143 s = 29 143 Figure 7 -14 C. M. Pascual 0 201 2. 00 Weight z 9
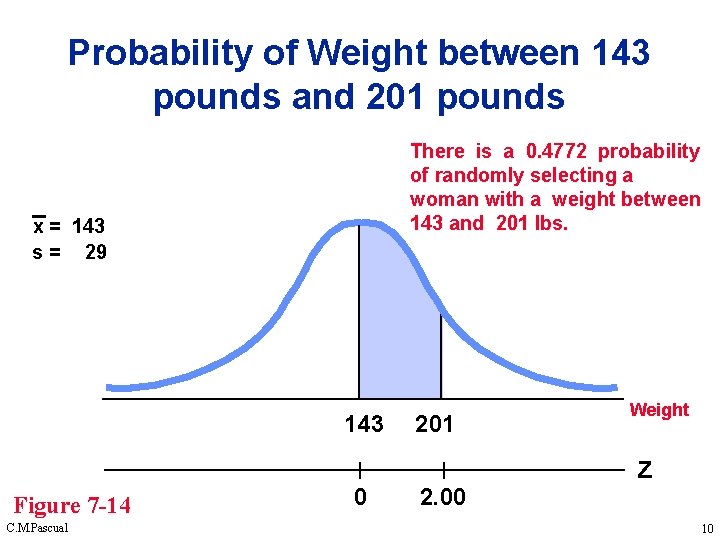
Probability of Weight between 143 pounds and 201 pounds There is a 0. 4772 probability of randomly selecting a woman with a weight between 143 and 201 lbs. x = 143 s = 29 143 Figure 7 -14 C. M. Pascual 0 201 2. 00 Weight z 10
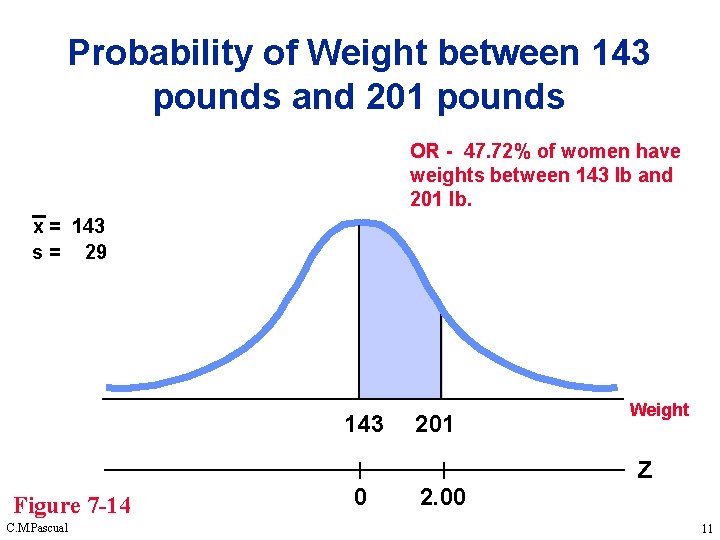
Probability of Weight between 143 pounds and 201 pounds OR - 47. 72% of women have weights between 143 lb and 201 lb. x = 143 s = 29 143 Figure 7 -14 C. M. Pascual 0 201 2. 00 Weight z 11
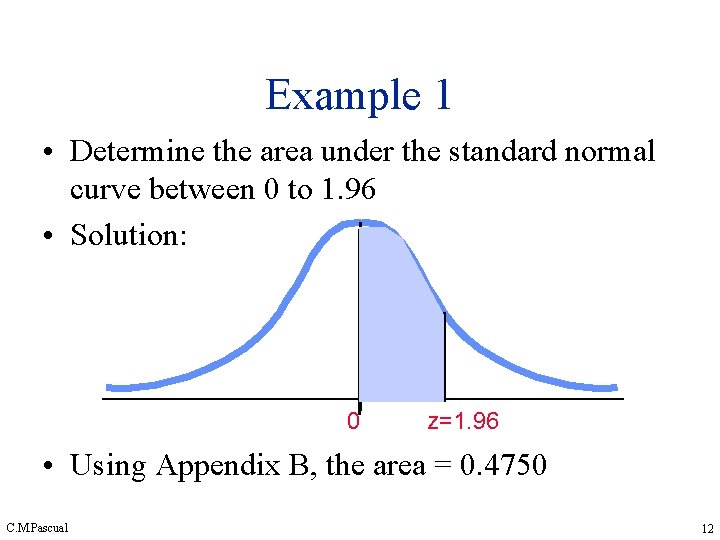
Example 1 • Determine the area under the standard normal curve between 0 to 1. 96 • Solution: 0 z=1. 96 • Using Appendix B, the area = 0. 4750 C. M. Pascual 12
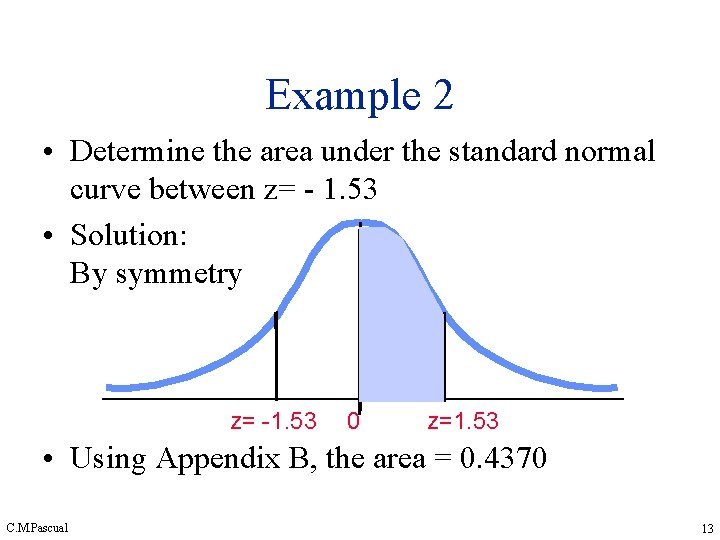
Example 2 • Determine the area under the standard normal curve between z= - 1. 53 • Solution: By symmetry z= -1. 53 0 z=1. 53 • Using Appendix B, the area = 0. 4370 C. M. Pascual 13
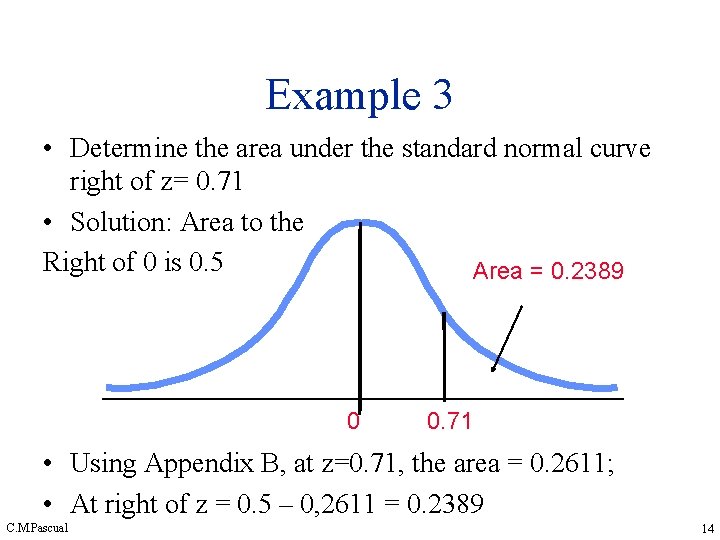
Example 3 • Determine the area under the standard normal curve right of z= 0. 71 • Solution: Area to the Right of 0 is 0. 5 Area = 0. 2389 0 0. 71 • Using Appendix B, at z=0. 71, the area = 0. 2611; • At right of z = 0. 5 – 0, 2611 = 0. 2389 C. M. Pascual 14

Example 4 • Find the area under the standard normal curve left of z= -2. 12 • Solution: By symmetry Area to the left of 0 is 0. 5 Area = 0. 4830 Area = 0. 2389 z = - 2. 12 0 • Using Appendix B, at z=0. 71, the area = 0. 4830; • At right of z = 0. 5 – 0. 4830 = 0. 0170 C. M. Pascual 15
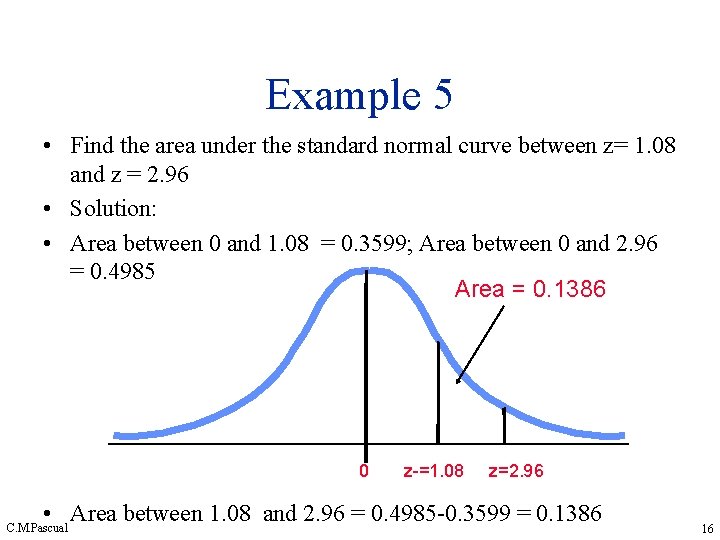
Example 5 • Find the area under the standard normal curve between z= 1. 08 and z = 2. 96 • Solution: • Area between 0 and 1. 08 = 0. 3599; Area between 0 and 2. 96 = 0. 4985 Area = 0. 1386 0 z-=1. 08 z=2. 96 • Area between 1. 08 and 2. 96 = 0. 4985 -0. 3599 = 0. 1386 C. M. Pascual 16
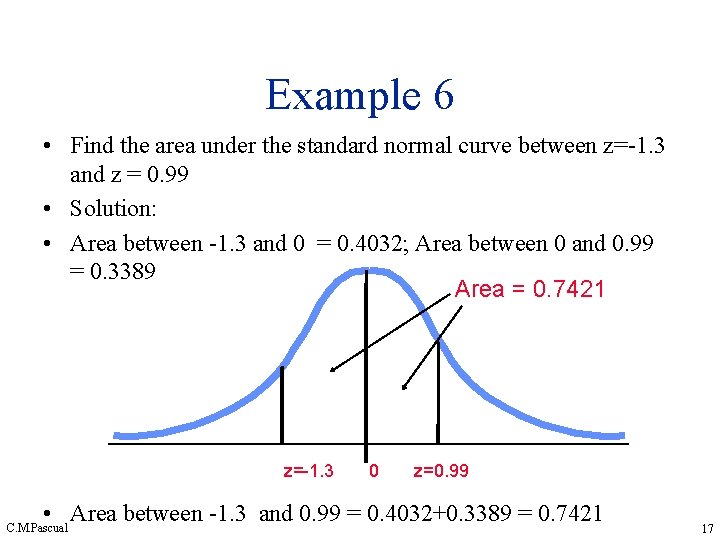
Example 6 • Find the area under the standard normal curve between z=-1. 3 and z = 0. 99 • Solution: • Area between -1. 3 and 0 = 0. 4032; Area between 0 and 0. 99 = 0. 3389 Area = 0. 7421 z=-1. 3 0 z=0. 99 • Area between -1. 3 and 0. 99 = 0. 4032+0. 3389 = 0. 7421 C. M. Pascual 17
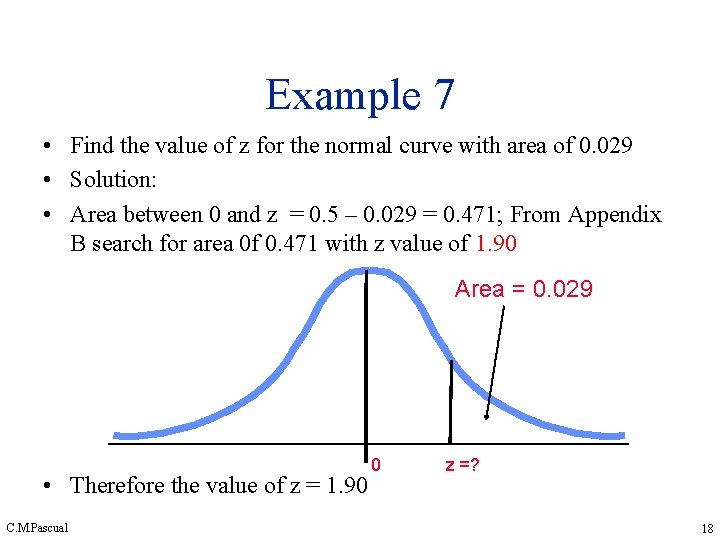
Example 7 • Find the value of z for the normal curve with area of 0. 029 • Solution: • Area between 0 and z = 0. 5 – 0. 029 = 0. 471; From Appendix B search for area 0 f 0. 471 with z value of 1. 90 Area = 0. 029 • Therefore the value of z = 1. 90 C. M. Pascual 0 z =? 18
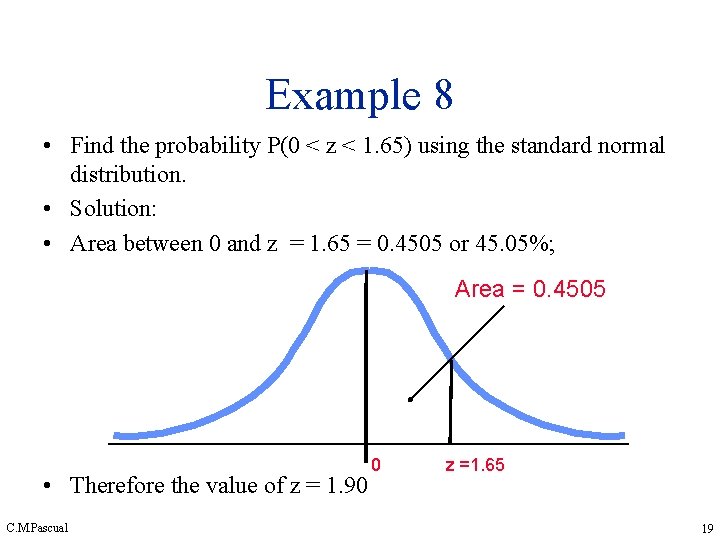
Example 8 • Find the probability P(0 < z < 1. 65) using the standard normal distribution. • Solution: • Area between 0 and z = 1. 65 = 0. 4505 or 45. 05%; Area = 0. 4505 • Therefore the value of z = 1. 90 C. M. Pascual 0 z =1. 65 19

Example 9 • Determine the value of z when x=12, µ=16 and σ = 3 • Solution: • Using the formula z = (x - µ)/ σ • = (12 – 16)/3 • = - 1. 33 C. M. Pascual 20

Example 10 • For a continuous random variable that has a normal distribution with mean of 20 and a standard deviation of 4, find the area under the normal curve from x=20 and x=27. • Solution: • Find standardize the normal distribution by converting the x values to z values: • Using the formula z = (x - µ)/ σ • z= (20 – 20)/4 = 0 and z = (27 – 20)/4 = 1. 75 • Then using Appendix B; at z= 1. 75; Area = 0. 4608 • The area between 0 and 1. 75 is 0. 4608 C. M. Pascual 21
- Slides: 21