ELEMENTARY STATISTICS Chapter 4 Probability Distributions MARIO F

ELEMENTARY STATISTICS Chapter 4 Probability Distributions MARIO F. TRIOLA EIGHTH Chapter 4. Section 4 -1 and 4 -2. Triola, Elementary Statistics, Eighth Edition. Copyright 2001. Addison Wesley Longman EDITION 1

Chapter 4 Probability Distributions 4 -1 Overview 4 -2 Random Variables 4 -3 Binomial Probability Distributions 4 -4 Mean, Variance, Standard Deviation for the Binomial Distribution Chapter 4. Section 4 -1 and 4 -2. Triola, Elementary Statistics, Eighth Edition. Copyright 2001. Addison Wesley Longman 2

4 -1 Overview This chapter will deal with the construction of probability distributions by combining the methods of Chapter 2 with the those of Chapter 3. Probability Distributions will describe what will probably happen instead of what actually did happen. Chapter 4. Section 4 -1 and 4 -2. Triola, Elementary Statistics, Eighth Edition. Copyright 2001. Addison Wesley Longman 3

Combining Descriptive Statistics Methods and Probabilities to Form a Theoretical Model of Behavior Figure 4 -1 Chapter 4. Section 4 -1 and 4 -2. Triola, Elementary Statistics, Eighth Edition. Copyright 2001. Addison Wesley Longman 4

4 -2 Random Variables Chapter 4. Section 4 -1 and 4 -2. Triola, Elementary

Definitions v Random Variable a variable (typically represented by x) that has a single numerical value, determined by chance, for each outcome of a procedure v. Probability Distribution a graph, table, or formula that gives the probability for each value of the random variable Chapter 4. Section 4 -1 and 4 -2. Triola, Elementary Statistics, Eighth Edition. Copyright 2001. Addison Wesley Longman 6

Table 4 -1 Probability Distribution Number of Girls Among Fourteen Newborn Babies x P(x) 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 0. 000 0. 001 0. 006 0. 022 0. 061 0. 122 0. 183 0. 209 0. 183 0. 122 0. 061 0. 022 0. 006 0. 001 0. 000 Chapter 4. Section 4 -1 and 4 -2. Triola, Elementary Statistics, Eighth Edition. Copyright 2001. Addison Wesley Longman 7

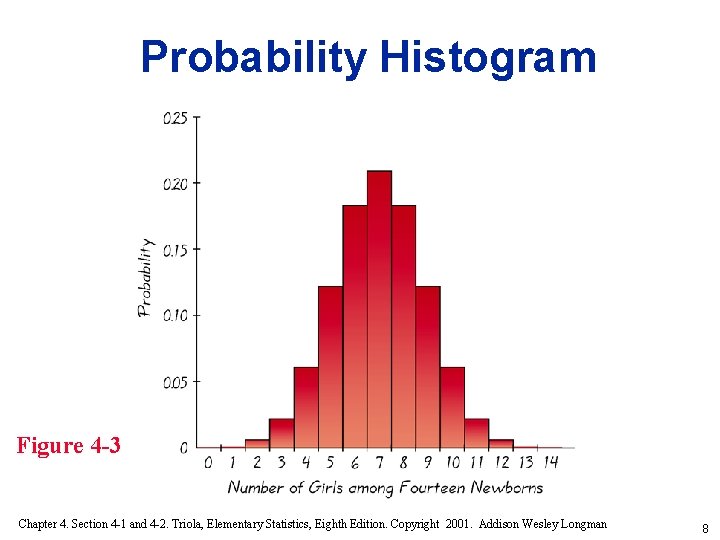
Probability Histogram Figure 4 -3 Chapter 4. Section 4 -1 and 4 -2. Triola,

Definitions v Discrete random variable has either a finite number of values or countable number of values, where ‘countable’ refers to the fact that there might be infinitely many values, but they result from a counting process. v Continuous random variable has infinitely many values, and those values can be associated with measurements on a continuous scale with no gaps or interruptions. Chapter 4. Section 4 -1 and 4 -2. Triola, Elementary Statistics, Eighth Edition. Copyright 2001. Addison Wesley Longman 9

Requirements for Probability Distribution The sum of all the probabilities of the distribution equals 1. ΣP(x) = 1 where x assumes all possible values All probabilities of the distribution must fall between 0 and 1 inclusive. 0 P(x) 1 for every value of x Chapter 4. Section 4 -1 and 4 -2. Triola, Elementary Statistics, Eighth Edition. Copyright 2001. Addison Wesley Longman 10

Mean, Variance and Standard Deviation of a Probability Distribution Mean µ = [x • P(x)] Variance 2 2 = [(x - µ) • P(x)] Standard Deviation = 2 Chapter 4. Section 4 -1 and 4 -2. Triola, Elementary Statistics, Eighth Edition. Copyright 2001. Addison Wesley Longman 11

Roundoff Rule for µ, , and 2 Round results by carrying one more decimal place than the number of decimal places used for the random variable x. If the values of x are integers, round µ, 2, and to one decimal place. Chapter 4. Section 4 -1 and 4 -2. Triola, Elementary Statistics, Eighth Edition. Copyright 2001. Addison Wesley Longman 12

Example A 4 point pop quiz was given and the scores ranged from 0 to 4, with the corresponding probabilities: 0. 05, 0. 25, 0. 3, 0. 2 • Write the probability distribution in a table. • Verify whether a probability distribution is given. • Compute the mean, variance and standard deviation of the probability distribution. Chapter 4. Section 4 -1 and 4 -2. Triola, Elementary Statistics, Eighth Edition. Copyright 2001. Addison Wesley Longman 13

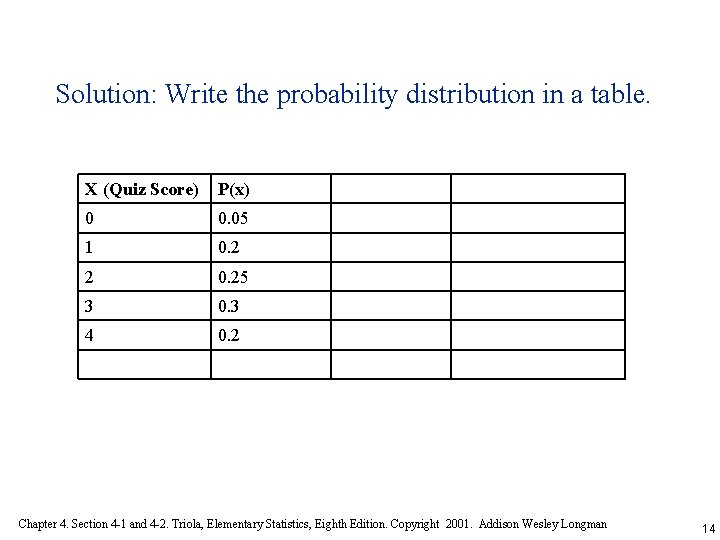
Solution: Write the probability distribution in a table. X (Quiz Score) P(x) 0 0. 05 1 0. 2 2 0. 25 3 0. 3 4 0. 2 Chapter 4. Section 4 -1 and 4 -2. Triola, Elementary Statistics, Eighth Edition. Copyright 2001. Addison Wesley Longman 14

Solution: Verify whether a probability distribution is given • Yes it is a probability distribution because the sum of P(x) for all values of x is 1 and P(x) for all values of x is between 0 and 1, inclusive. X (Quiz Scores) P(x) 0 0. 05 1 0. 2 2 0. 25 3 0. 3 4 0. 2 Sum 1. 0 Chapter 4. Section 4 -1 and 4 -2. Triola, Elementary Statistics, Eighth Edition. Copyright 2001. Addison Wesley Longman 15

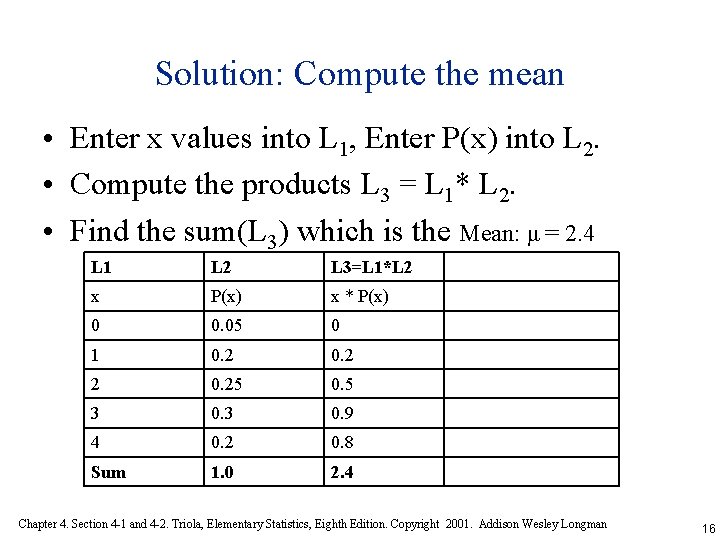
Solution: Compute the mean • Enter x values into L 1, Enter P(x) into L 2. • Compute the products L 3 = L 1* L 2. • Find the sum(L 3) which is the Mean: μ = 2. 4 L 1 L 2 L 3=L 1*L 2 x P(x) x * P(x) 0 0. 05 0 1 0. 2 2 0. 25 0. 5 3 0. 9 4 0. 2 0. 8 Sum 1. 0 2. 4 Chapter 4. Section 4 -1 and 4 -2. Triola, Elementary Statistics, Eighth Edition. Copyright 2001. Addison Wesley Longman 16

Solution: Compute the variance and standard deviation. • • Having already found the mean of 2. 4 Compute L 4 = (L 1 - 2. 4)2* L 2. Find the sum(L 4) which is the 2 = 1. 34 1. 3 Find the which is the square root of 2 = = 1. 16 1. 2 L 1 L 2 L 3 = L 1*L 2 L 4=(L 1 -2. 4)2*L 2 x P(x) x * P(x) (x- μ)2*P(x) 0 0. 05 0 (0 -2. 4)2*0. 05 = 0. 288 1 0. 2 (1 -2. 4)2*0. 2 = 0. 392 2 0. 25 0. 5 (2 -2. 4)2*0. 25 = 0. 040 3 0. 9 (3 -2. 4)2*0. 3 = 0. 108 4 0. 2 0. 8 (4 -2. 4)2*0. 2 = 0. 512 Sum 1. 0 2. 4 1. 34 Chapter 4. Section 4 -1 and 4 -2. Triola, Elementary Statistics, Eighth Edition. Copyright 2001. Addison Wesley Longman 17

Definition Expected Value The average(mean) value of outcomes, if the trials could continue indefinetly. E = [x • P(x)] Chapter 4. Section 4 -1 and 4 -2. Triola, Elementary Statistics, Eighth Edition. Copyright 2001. Addison Wesley Longman 18

The Daily Number allows you to place a bet that the three-digit number of your choice. It cost $1 to place a bet in order to win $500. What is the expected value of gain or loss? Chapter 4. Section 4 -1 and 4 -2. Triola, Elementary Statistics, Eighth Edition. Copyright 2001. Addison Wesley Longman 19

E = [x • P(x)] Event x Win $499 Lose - $1 Chapter 4.

E = [x • P(x)] Event x P(x) Win $499 0. 001 Lose -

E = [x • P(x)] Event x P(x) x • P(x) Win $499 0. 001 0. 499 Lose - $1 0. 999 - 0. 999 Chapter 4. Section 4 -1 and 4 -2. Triola, Elementary Statistics, Eighth Edition. Copyright 2001. Addison Wesley Longman 22

E = [x • P(x)] Event x P(x) x • P(x) Win $499 0. 001 0. 499 Lose - $1 0. 999 - 0. 999 E = -$. 50 Chapter 4. Section 4 -1 and 4 -2. Triola, Elementary Statistics, Eighth Edition. Copyright 2001. Addison Wesley Longman 23

Expected Value • This means that in the long run, for each $1 bet, we can expect to lose an average of $. 50. • In actuality a player either loses $1 or wins $499, there will never be a loss of $. 50. • If an expected value is $0, that means that the game is fair, and favors no side of the bet. Chapter 4. Section 4 -1 and 4 -2. Triola, Elementary Statistics, Eighth Edition. Copyright 2001. Addison Wesley Longman 24

Alternate Solution: Excluding the cost of playing. Event x P(x) x • P(x) Win $500 0. 001 0. 50 Lose 0 0. 999 0 E = $. 50, Which means the average win is $. 50. If the game cost $. 50 to play E = 0 and it would be a “fair” game and not favor either side of the bet. If the game cost $. 75 to play E = -. 25 and it would not be a “fair” game and would favor the house. Chapter 4. Section 4 -1 and 4 -2. Triola, Elementary Statistics, Eighth Edition. Copyright 2001. Addison Wesley Longman 25