ELEMENTARY STATISTICS BLUMAN Confidence Interval and Sample Size

ELEMENTARY STATISTICS, BLUMAN Confidence Interval and Sample Size for Proportion © 2019 Mc. Graw-Hill Education. All rights reserved. Authorized only for instructor use in the classroom. No reproduction or further distribution permitted without the prior written consent of Mc. Graw-Hill Education.

Objectives for this Power. Point Construct a confidence interval for the estimate of a

This section involves finding confidence intervals and sample size for proportions. A proportion represents a part of a whole. Proportions may be obtained either from samples or populations. © 2019 Mc. Graw-Hill Education

Symbols Used in Proportion Notation For a sample proportion, where X = number of

Confidence Interval for a Proportion © 2019 Mc. Graw-Hill Education

Problem In a clinical study for a pain medication, 26 out of 558 participants experienced dizziness. Find the 90% confidence interval estimate of the proportion of the population that would expect to experience dizziness while taking this particular pain medication. © 2019 Mc. Graw-Hill Education

Sample Proportion © 2019 Mc. Graw-Hill Education

Point Estimate © 2019 Mc. Graw-Hill Education

Margin of Error © 2019 Mc. Graw-Hill Education

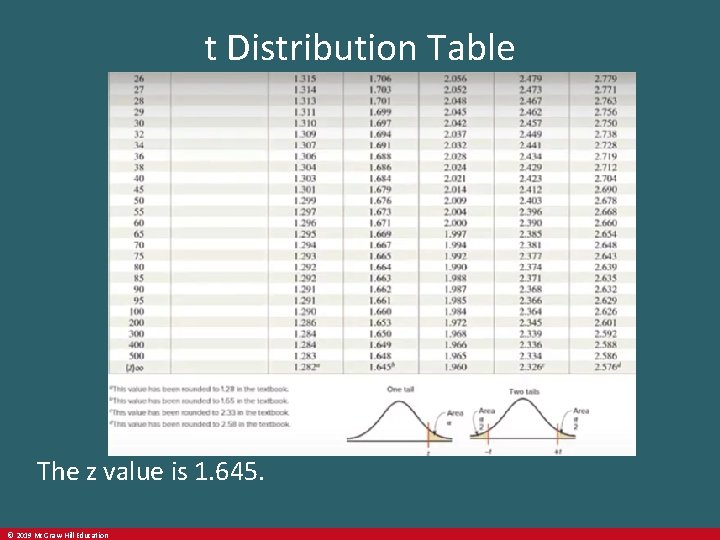
t Distribution Table The z value is 1. 645. © 2019 Mc. Graw-Hill Education

Calculation for Margin of Error © 2019 Mc. Graw-Hill Education

Formula for Confidence Interval for a Proportion © 2019 Mc. Graw-Hill Education

Interval in Decimal Format We have an interval that spans from. 0319 to. 0613. We can use this interval as an estimate for the population proportion. This interval is interpreted in the following way: It can be stated with 90% confidence that the proportion of the population that would expect to experience dizziness while taking this particular pain medication is between 0. 0319 and. 0613. © 2019 Mc. Graw-Hill Education

Interval in Percentage Format We can also interpret this interval in a percentage format. It can be stated with 90% confidence that between 3. 19% and 6. 13% of the population would expect to experience dizziness while taking this particular pain medication. © 2019 Mc. Graw-Hill Education

Formula for Minimum Sample Size n Needed for Interval Estimate of a Population Proportion If necessary, round up to obtain a whole number. There are two situations to consider. First, if some approximation of is known (e. g. , from a previous study), that value can be used in the formula. Second, if no approximation of is known, you should use © 2019 Mc. Graw-Hill Education