Elementary maths for GMT Algorithm analysis Trees Part

Elementary maths for GMT Algorithm analysis Trees

Part I: Binary Search Trees

Goal • Analyzing data structures • Example: binary search trees • Overview – Definition – Properties – Operations • Analyzing properties and running times of operations Elementary maths for GMT – Algorithm analysis - Trees 3

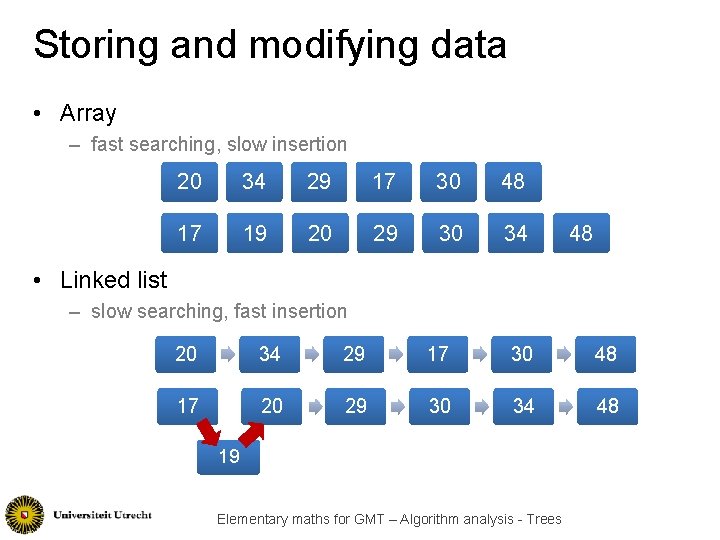
Storing and modifying data • Array – fast searching, slow insertion 20 34 29 17 30 48 17 19 20 29 30 34 48 • Linked list – slow searching, fast insertion 20 34 29 17 30 48 17 20 29 30 34 48 19 Elementary maths for GMT – Algorithm analysis - Trees

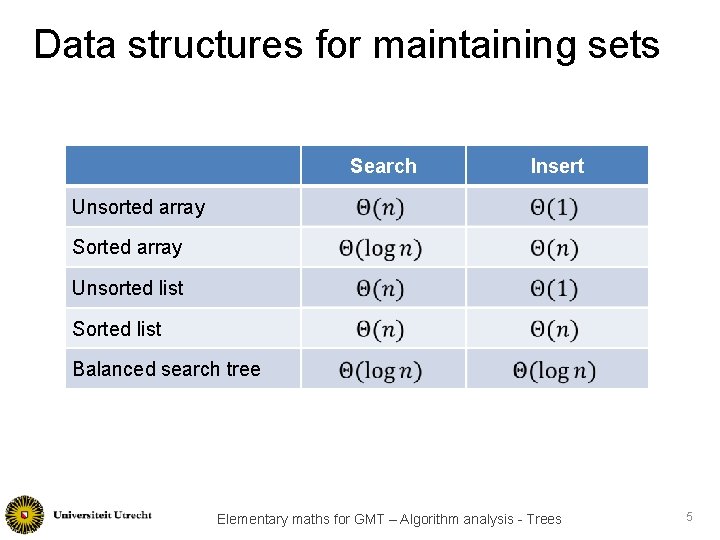
Data structures for maintaining sets Search Insert Unsorted array Sorted array Unsorted list Sorted list Balanced search tree Elementary maths for GMT – Algorithm analysis - Trees 5

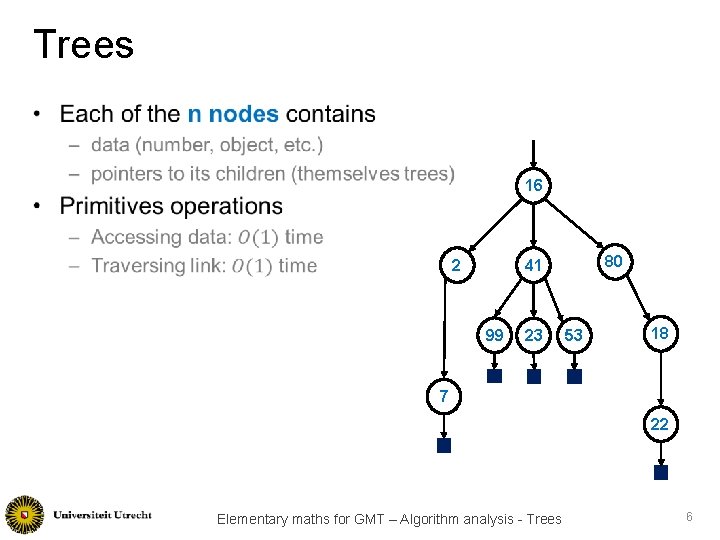
Trees • 16 2 80 41 99 23 53 18 7 22 Elementary maths for GMT – Algorithm analysis - Trees 6

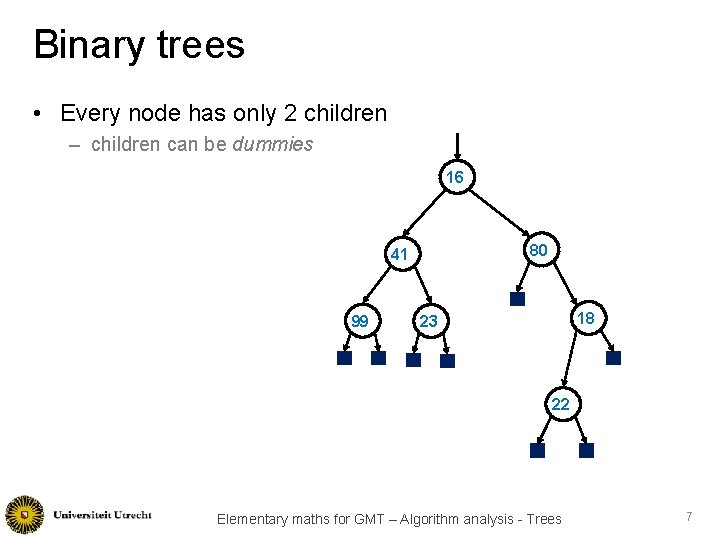
Binary trees • Every node has only 2 children – children can be dummies 16 80 41 99 18 23 22 Elementary maths for GMT – Algorithm analysis - Trees 7

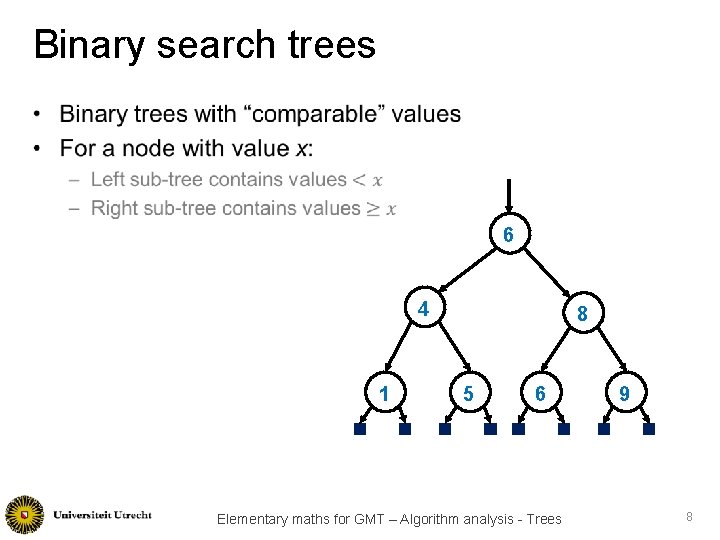
Binary search trees • 6 4 1 8 5 6 Elementary maths for GMT – Algorithm analysis - Trees 9 8

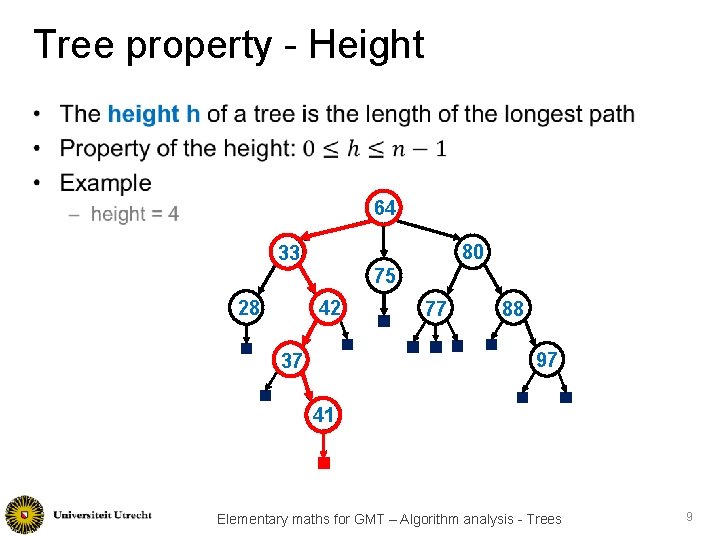
Tree property - Height • 64 80 33 75 28 42 77 88 97 37 41 Elementary maths for GMT – Algorithm analysis - Trees 9

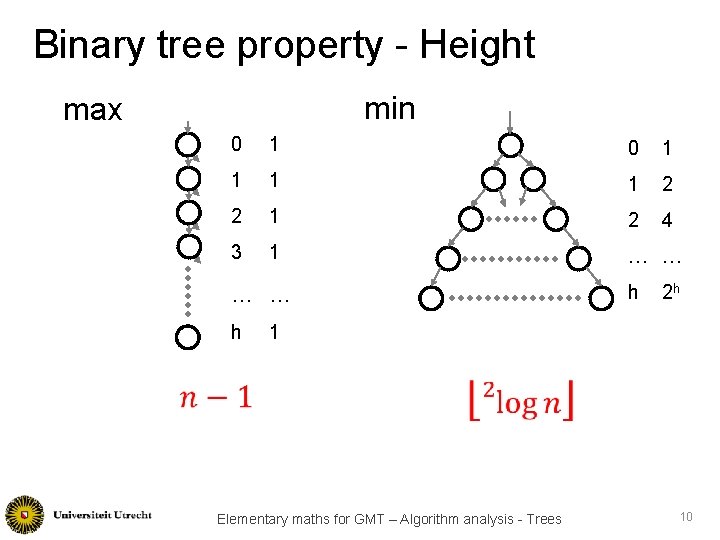
Binary tree property - Height min max 0 1 1 1 1 2 2 1 2 4 3 1 … … h h 2 h 1 Elementary maths for GMT – Algorithm analysis - Trees 10

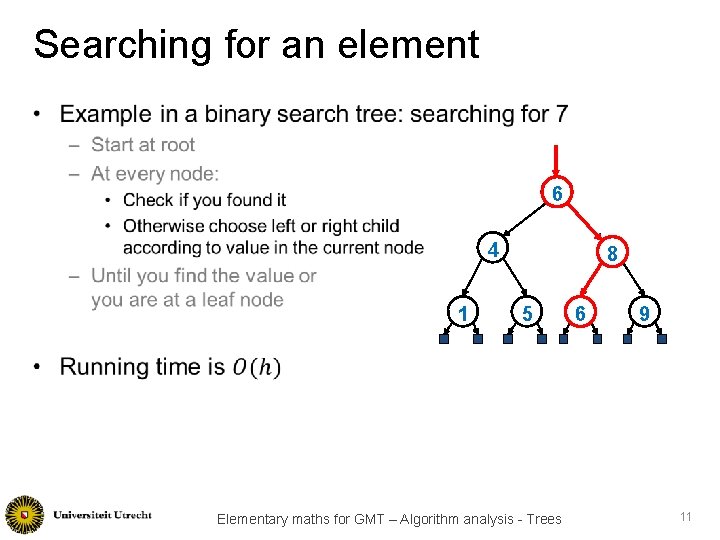
Searching for an element • 6 4 1 8 5 Elementary maths for GMT – Algorithm analysis - Trees 6 9 11

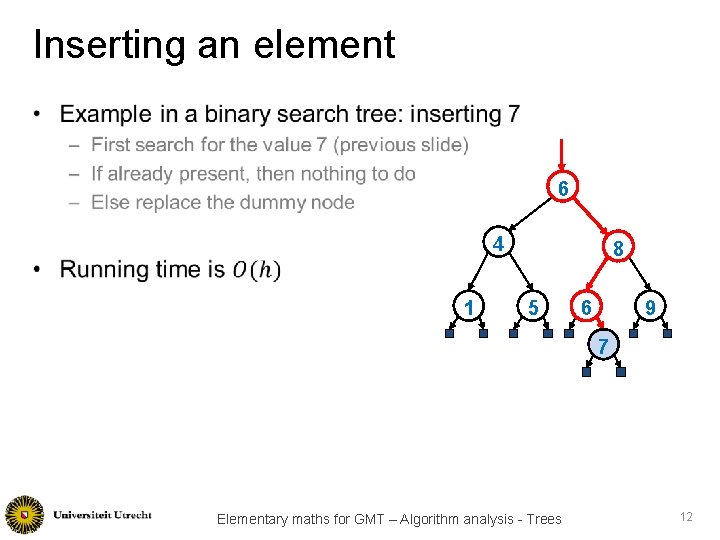
Inserting an element • 6 4 1 8 5 6 9 7 Elementary maths for GMT – Algorithm analysis - Trees 12

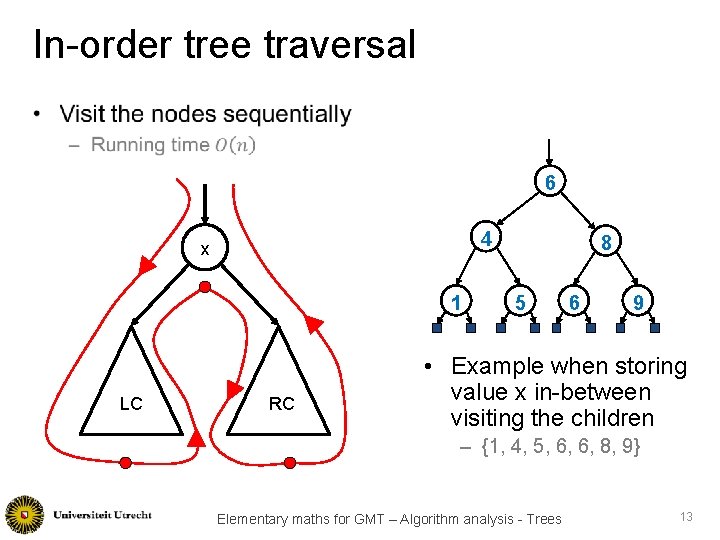
In-order tree traversal • 6 4 x 1 LC RC 8 5 6 9 • Example when storing value x in-between visiting the children – {1, 4, 5, 6, 6, 8, 9} Elementary maths for GMT – Algorithm analysis - Trees 13

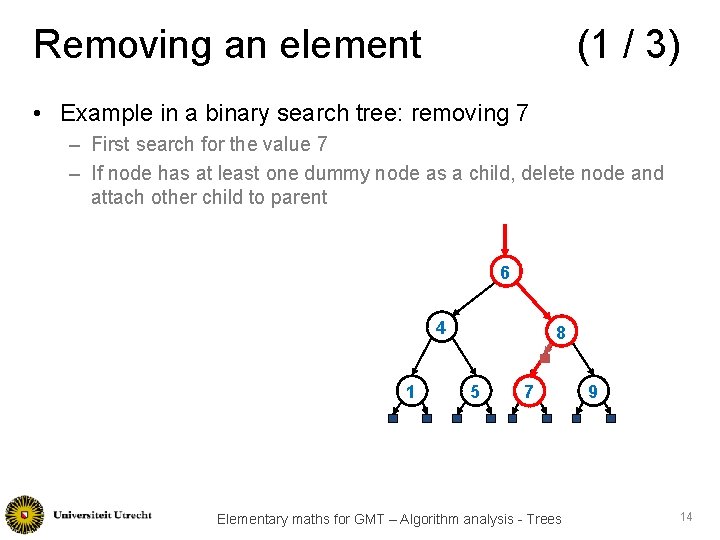
Removing an element (1 / 3) • Example in a binary search tree: removing 7 – First search for the value 7 – If node has at least one dummy node as a child, delete node and attach other child to parent 6 4 1 8 5 7 Elementary maths for GMT – Algorithm analysis - Trees 9 14

Removing an element (2 / 3) • Example in a binary search tree: removing 8 – Search for 8 – If left (resp. right) child is a dummy node, attach right (resp. left) child to parent 6 4 1 9 8 5 Elementary maths for GMT – Algorithm analysis - Trees 9 15

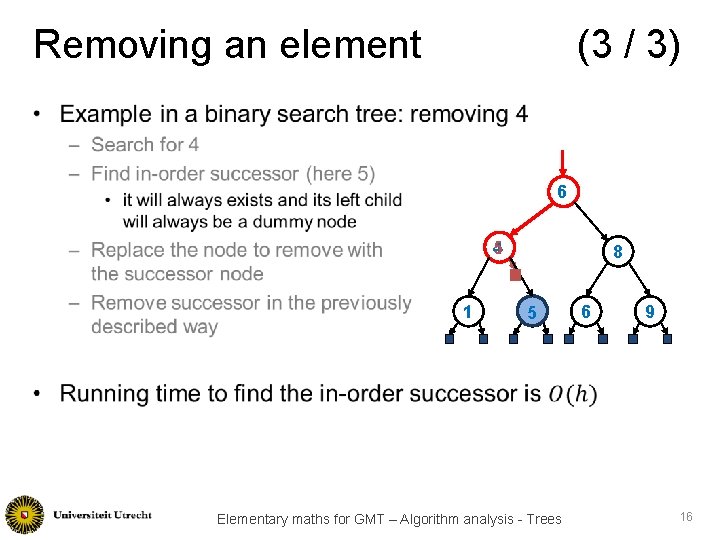
Removing an element (3 / 3) • 6 4 5 1 8 5 Elementary maths for GMT – Algorithm analysis - Trees 6 9 16

Summary on binary search trees Parameter / Operation Property / Time Height h Accessing data, traversing a link In-order traversal Search, insertion and removal Elementary maths for GMT – Algorithm analysis - Trees 17

Part II: AVL trees

AVL tree: a balanced binary tree • An AVL tree (Adelson-Velskii Landis) is a binary search tree where for every internal node v, the heights of the children of v can differ at most by 1 • Example where the heights are shown next to the nodes 3 6 1 2 4 11 0 14 8 5 0 7 0 9 Elementary maths for GMT – Algorithm analysis - Trees 19

Height of an AVL tree • Elementary maths for GMT – Algorithm analysis - Trees 20

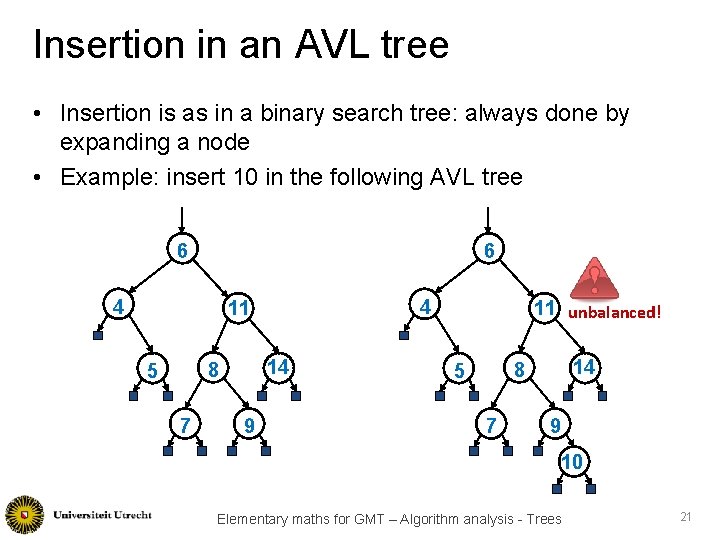
Insertion in an AVL tree • Insertion is as in a binary search tree: always done by expanding a node • Example: insert 10 in the following AVL tree 6 6 4 4 11 14 8 5 7 9 11 unbalanced! 14 8 5 7 9 10 Elementary maths for GMT – Algorithm analysis - Trees 21

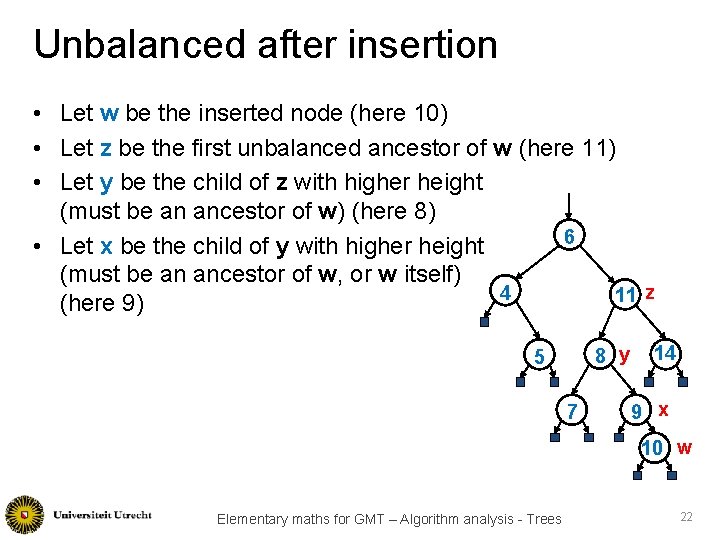
Unbalanced after insertion • Let w be the inserted node (here 10) • Let z be the first unbalanced ancestor of w (here 11) • Let y be the child of z with higher height (must be an ancestor of w) (here 8) 6 • Let x be the child of y with higher height (must be an ancestor of w, or w itself) 4 11 z (here 9) 8 y 5 7 14 9 x 10 w Elementary maths for GMT – Algorithm analysis - Trees 22

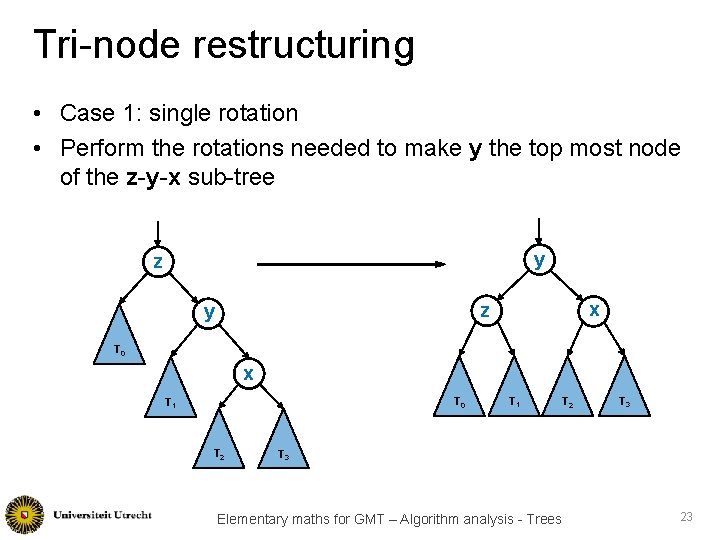
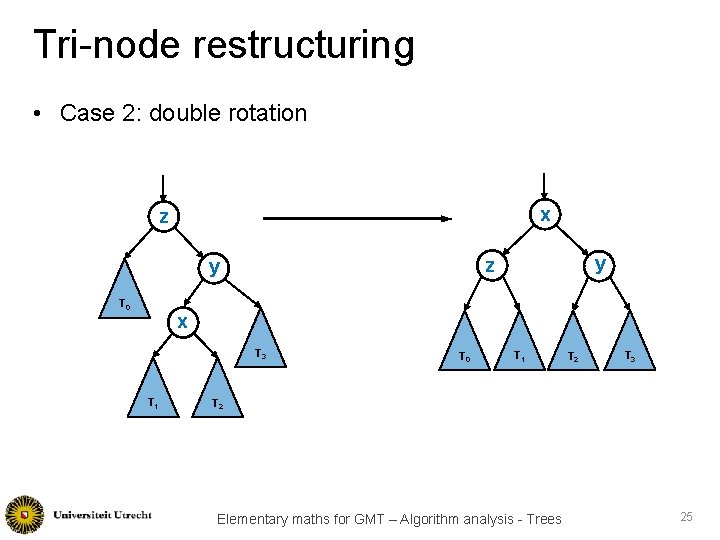
Tri-node restructuring • Case 1: single rotation • Perform the rotations needed to make y the top most node of the z-y-x sub-tree y z x z y T 0 x T 0 T 1 T 2 T 3 Elementary maths for GMT – Algorithm analysis - Trees 23

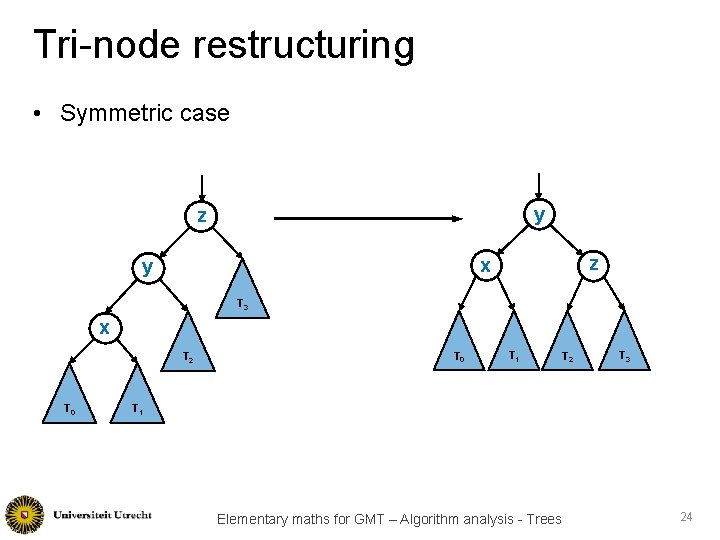
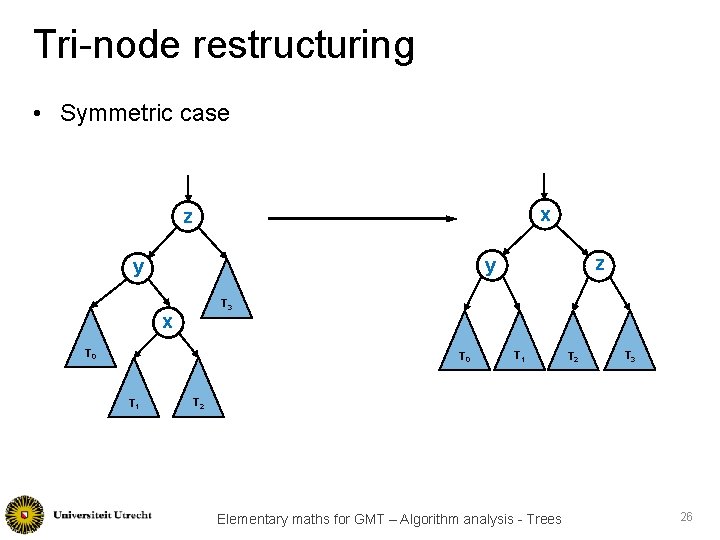
Tri-node restructuring • Symmetric case y z z x y T 3 x T 2 T 0 T 1 T 2 T 3 T 1 Elementary maths for GMT – Algorithm analysis - Trees 24

Tri-node restructuring • Case 2: double rotation x z T 0 y z y x T 3 T 1 T 0 T 1 T 2 T 3 T 2 Elementary maths for GMT – Algorithm analysis - Trees 25

Tri-node restructuring • Symmetric case x z T 3 x T 0 T 1 z y y T 1 T 2 T 3 T 2 Elementary maths for GMT – Algorithm analysis - Trees 26

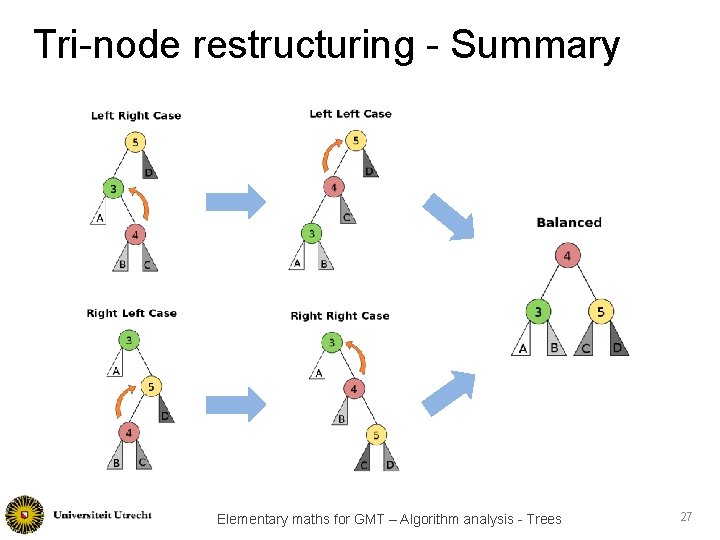
Tri-node restructuring - Summary Elementary maths for GMT – Algorithm analysis - Trees 27

Removal in an AVL tree • Removal begins as in a binary search tree, which means the node removed will become an empty node • Example: remove 5 in the following AVL tree 6 6 unbalanced! 4 11 7 11 14 8 5 4 9 14 8 17 7 Elementary maths for GMT – Algorithm analysis - Trees 9 17 28

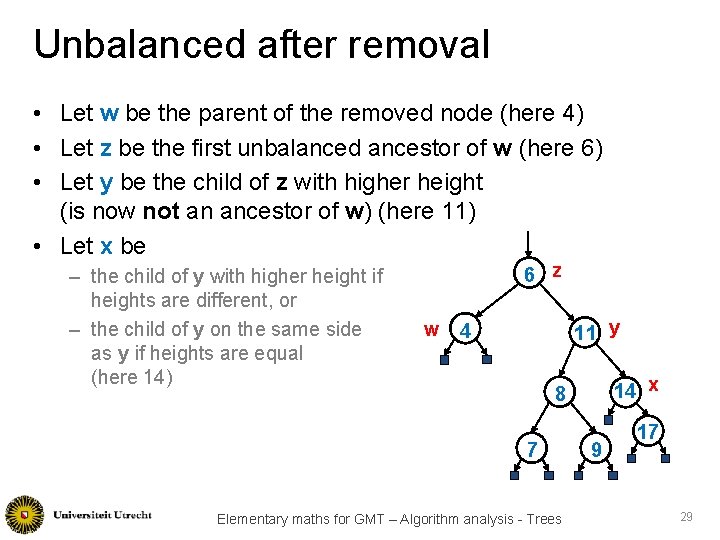
Unbalanced after removal • Let w be the parent of the removed node (here 4) • Let z be the first unbalanced ancestor of w (here 6) • Let y be the child of z with higher height (is now not an ancestor of w) (here 11) • Let x be – the child of y with higher height if heights are different, or – the child of y on the same side as y if heights are equal (here 14) 6 z w 11 y 4 14 x 8 7 Elementary maths for GMT – Algorithm analysis - Trees 9 17 29

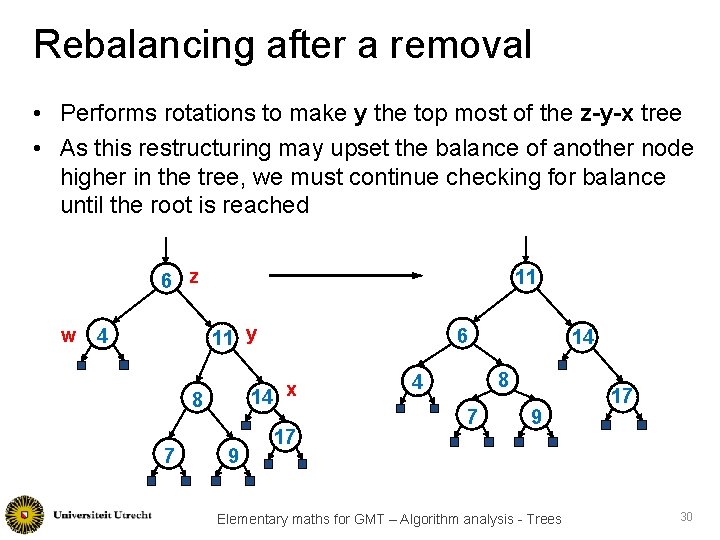
Rebalancing after a removal • Performs rotations to make y the top most of the z-y-x tree • As this restructuring may upset the balance of another node higher in the tree, we must continue checking for balance until the root is reached 6 z w 11 11 y 4 14 x 8 7 6 9 17 14 8 4 7 9 Elementary maths for GMT – Algorithm analysis - Trees 17 30

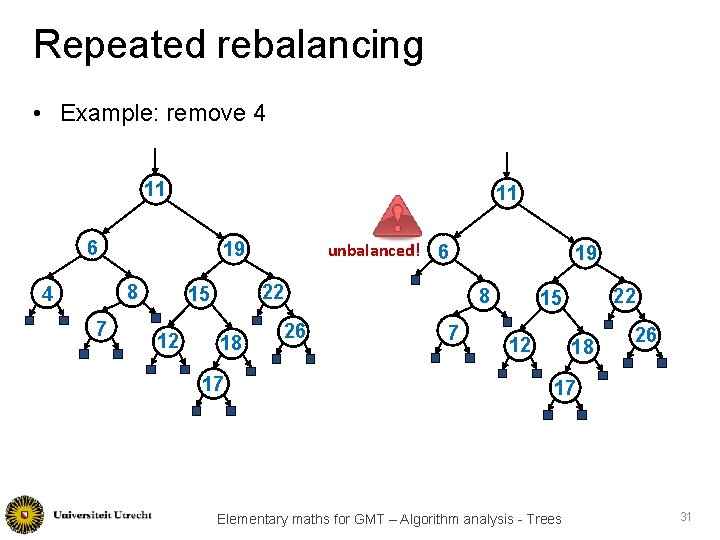
Repeated rebalancing • Example: remove 4 11 11 6 19 8 4 7 6 22 15 12 unbalanced! 18 17 26 19 8 7 22 15 12 18 26 17 Elementary maths for GMT – Algorithm analysis - Trees 31

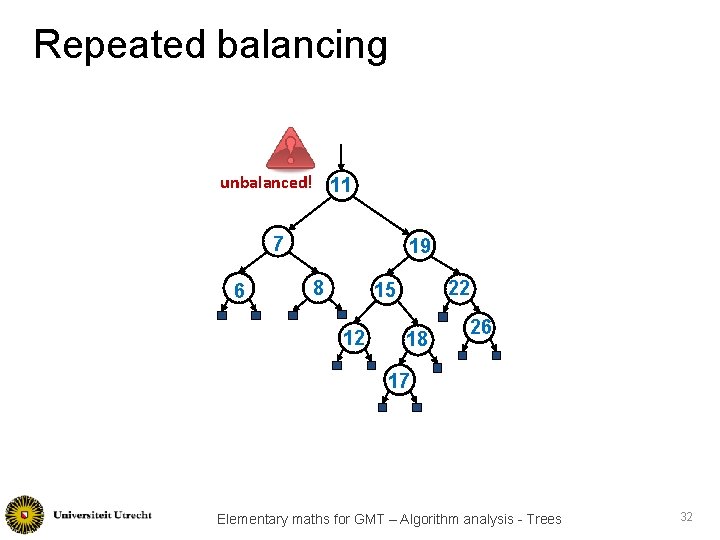
Repeated balancing unbalanced! 11 7 6 19 8 22 15 12 18 26 17 Elementary maths for GMT – Algorithm analysis - Trees 32

Running times for AVL trees • Elementary maths for GMT – Algorithm analysis - Trees 33

AVL trees vs. hash tables • Elementary maths for GMT – Algorithm analysis - Trees 34

Other trees • Elementary maths for GMT – Algorithm analysis - Trees 35