Elementary Linear Algebra 4 1 Real Vector Spaces

Elementary Linear Algebra 4. 1 Real Vector Spaces 4. 2 Subspaces 4. 3 Linear Independence 4. 4 Coordinates and Basis 4. 5 Dimension 4. 6 Change of Basis 4. 7 Row Space, Column Space, and Null Space 4. 8 Rank, Nullity, and the Fundamental Matrix Spaces

Definition 1. 1: Definition: Let V be an arbitrary non empty set of objects on which two operations are defined (1) addition and (2) multiplication by scalars ( V, + ; R ) A vector space (over R) consists of a set V along with 2 operations ‘+’ and ‘* ’ s. t. (1) For the vector addition + : v, w, u V a) v + w V b) v + w = w + v c) ( v + w ) + u = v + ( w + u ) d) 0 V s. t. v + 0 = v e) v V s. t. v v = 0 (2) For the scalar multiplication : v, w V and a, b R, f) a v V g) ( a + b ) v = a v + b v h) a ( v + w ) = a v + a w i) ( a b ) v = a ( b v ) = a b v a) 1 v = v ( Closure ) ( Commutativity ) ( Associativity ) ( Zero element ) ( Inverse ) [ R is the real number field (R, +, ) ] ( Closure ) ( Distributivity ) ( Associativity )

To Show that a Set with Two Operations is a Vector Space 1. Identify the set V of objects that will become vectors. 2. Identify the addition and scalar multiplication operations on V. 3. Verify Axioms 1(closure under addition) and 6 (closure under scalar multiplication) ; that is, adding two vectors in V produces a vector in V, and multiplying a vector in V by a scalar also produces a vector in V. 4. Confirm that Axioms 2, 3, 4, 5, 7, 8, 9 and 10 hold.

Examples 1. The set V of real and complex numbers. 2. The set of polynomials of order n. 3. The set of all matrix of order m*n

Counter Examples

Example : R 2 is a vector space if with Example : Plane in R 3. The plane through the origin is a vector space.

Example : Space of Real Polynomials of Degree n or less, Pn E. g. , The kth component of a is Pn is a vector space with vectors Vector addition: i. e. , Scalar multiplication: Zero element: Inverse: Pn is isomorphic to Rn+1 with i. e. ,

Example : Function Space The set { f | f : N → R } of all real valued functions of natural numbers is a vector space if Vector addition: Scalar multiplication: Zero element: Inverse: f ( n ) is a vector of countably infinite dimensions: f = ( f(0), f(1), f(2), f(3), … ) E. g. , ~

Example : Solution Space of a Linear Homogeneous Differential Equation is a vector space with Vector addition: Scalar multiplication: Zero element: Inverse: Closure: →

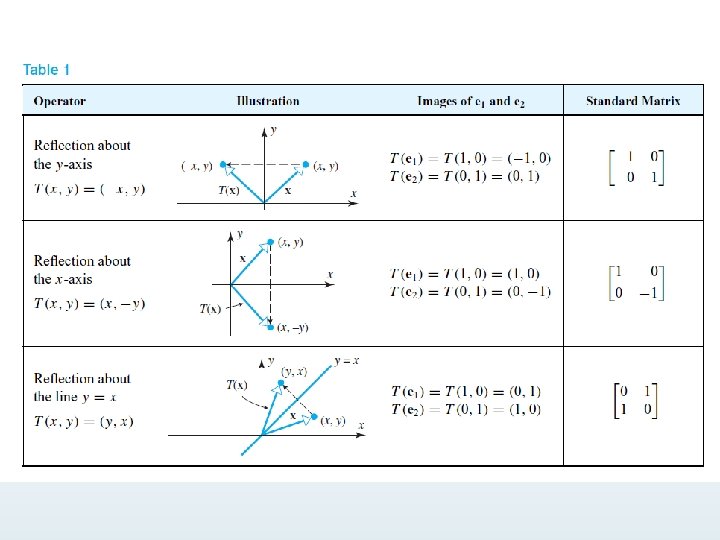
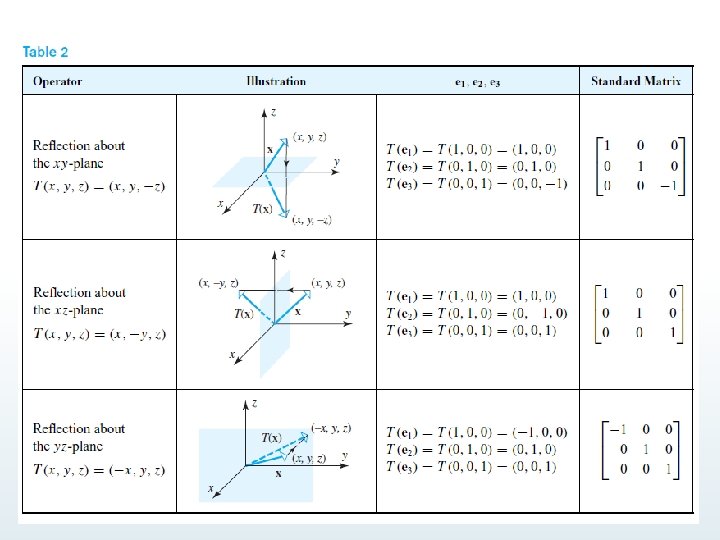
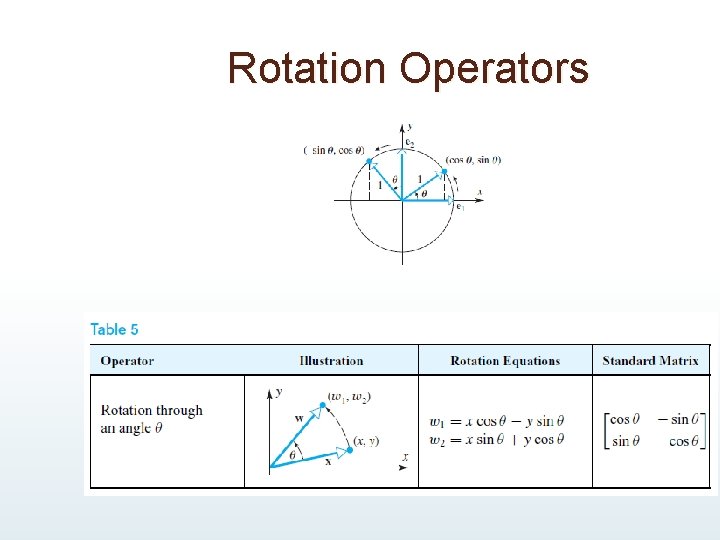
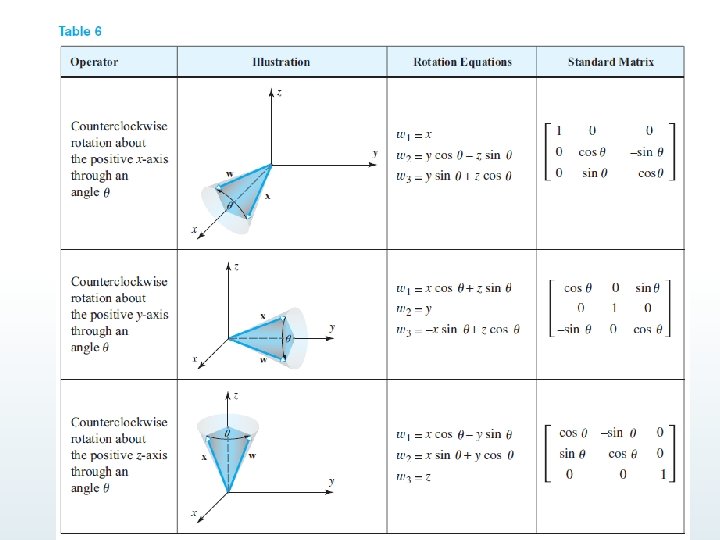
Rotation Operators

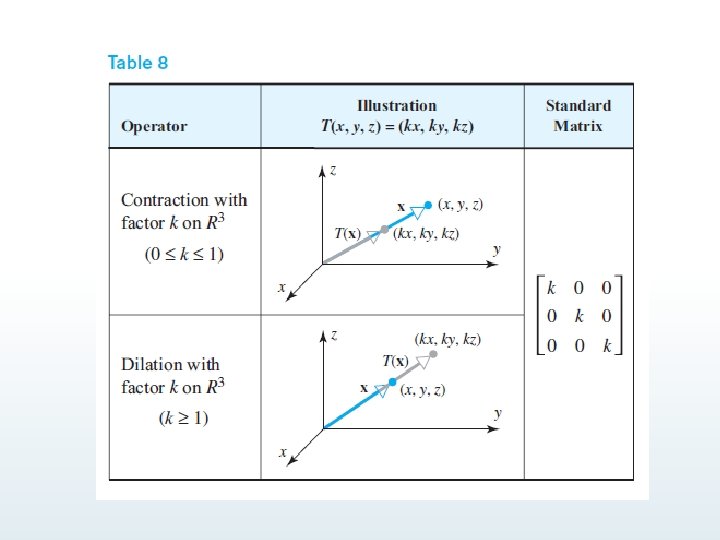
Dilations and Contractions

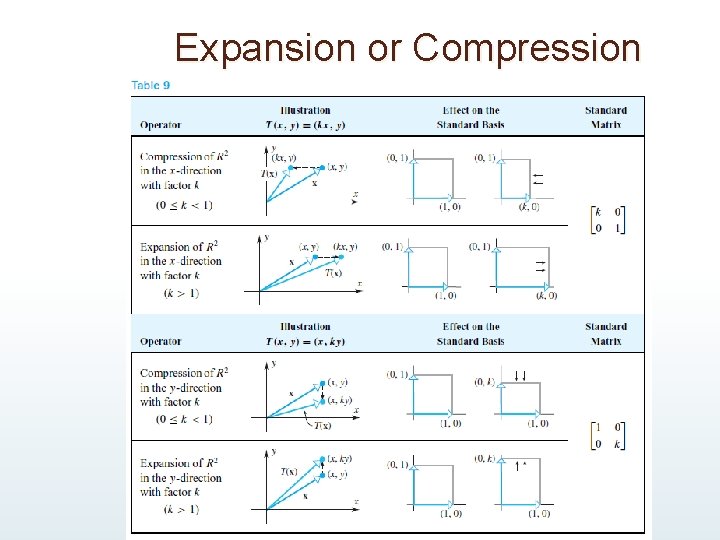
Expansion or Compression

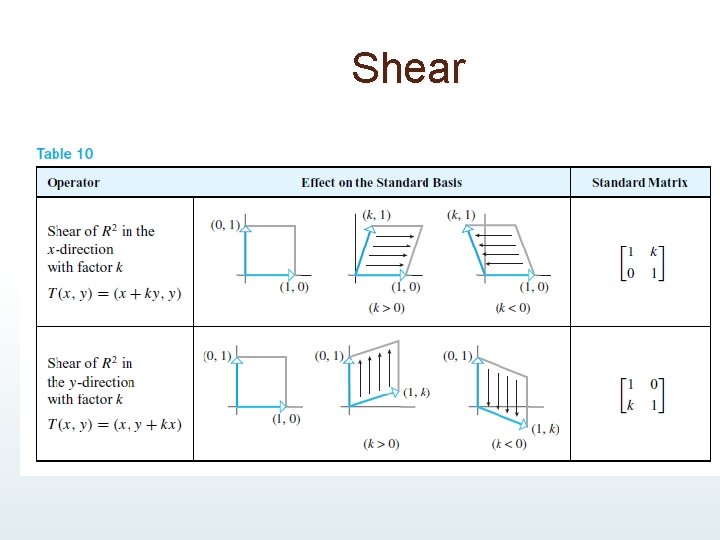
Shear