ELECTROSTATICS III Electrostatic Potential and Gausss Theorem 1

ELECTROSTATICS - III - Electrostatic Potential and Gauss’s Theorem 1. Line Integral of Electric Field 2. Electric Potential and Potential Difference 3. Electric Potential due to a Single Point Charge 4. Electric Potential due to a Group of Charges 5. Electric Potential due to an Electric Dipole 6. Equipotential Surfaces and their Properties 7. Electrostatic Potential Energy 8. Area Vector, Solid Angle, Electric Flux 9. Gauss’s Theorem and its Proof 10. Coulomb’s Law from Gauss’s Theorem 11. Applications of Gauss’s Theorem: 12. Electric Field Intensity due to Line Charge, Plane Sheet of Charge and Spherical Shell Created by C. Mani, Principal, K V No. 1, AFS, Jalahalli West, Bangalore

Line Integral of Electric Field (Work Done by Electric Field): Negative Line Integral of Electric Field represents the work done by the electric field on a unit positive charge in moving it from one point to another in the electric field. B Y WAB = d. W = - E. dl A A Let q 0 be the test charge in place of the unit positive charge. r. A The force F = +q 0 E acts on the test charge due to the source charge +q. +q It is radially outward and tends to accelerate the test charge. To prevent this acceleration, equal and opposite force –q 0 E has to be applied on the test charge. F +q 0 r r. B B X O Z Total work done by the electric field on the test charge in moving it from A to B in the electric field is B WAB = d. W = - E. dl = A qq 0 4πε 0 1 [r B - 1 r. A ]

B WAB = d. W = - E. dl = A qq 0 4πε 0 1 [r B - 1 r. A ] 1. The equation shows that the work done in moving a test charge q 0 from point A to another point B along any path AB in an electric field due to +q charge depends only on the positions of these points and is independent of the actual path followed between A and B. 2. That is, the line integral of electric field is path independent. 3. Therefore, electric field is ‘conservative field’. 4. Line integral of electric field over a closed path is zero. This is another condition satisfied by conservative field. B E. dl = 0 Note: A Line integral of only static electric field is independent of the path followed. However, line integral of the field due to a moving charge is not independent of the path because the field varies with time.

Electric Potential: Electric potential is a physical quantity which determines the flow of charges from one body to another. It is a physical quantity that determines the degree of electrification of a body. Electric Potential at a point in the electric field is defined as the work done in moving (without any acceleration) a unit positive charge from infinity to that point against the electrostatic force irrespective of the path followed. B E. dl = WAB = A qq 0 4πε 0 According to definition, 1 [r B - 1 r. A ] or WAB q 0 = q 4πε 0 1 [r - B 1 r. A = ∞ and r. B = r (where r is the distance from the source charge and the point of consideration) W∞B q 0 = q 4πε 0 r =V W∞B V= q 0 SI unit of electric potential is volt (V) or J C-1 or Nm C-1. Electric potential at a point is one volt if one joule of work is done in moving one coulomb charge from infinity to that point in the electric field. ]

Electric Potential Difference: Electric Potential Difference between any two points in the electric field is defined as the work done in moving (without any acceleration) a unit positive charge from one point to the other against the electrostatic force irrespective of the path followed. B E. dl = WAB = A qq 0 4πε 0 1 [r - B WAB q 0 = 1 r. A q 4πε 0 ] 1 r. B WAB q 0 = or - VB - V A q 4πε 0 1 r. A q 4πε 0 1 [r B - 1 r. A ] = V B - VA WAB = ∆V = q 0 1. Electric potential and potential difference are scalar quantities. 2. Electric potential at infinity is zero. 3. Electric potential near an isolated positive charge (q > 0) is positive and that near an isolated negative charge (q < 0) is negative. 4. cgs unit of electric potential is stat volt. 1 stat volt = 1 erg / stat coulomb

Electric Potential due to a Single Point Charge: Let +q 0 be the test charge placed at P at a distance x from the source charge +q. E dx +q 0 B +q Q q 0 E ∞ P r The force F = +q 0 E is radially outward and tends to accelerate the test charge. x To prevent this acceleration, equal and opposite force –q 0 E has to be applied on the test charge. Work done to move q 0 from P to Q through ‘dx’ against q 0 E is d. W = F. dx = q 0 E. dx d. W = - q q 0 4πε 0 x 2 dx or E= d. W = q 0 E dx cos 180° = - q 0 E dx q 4πε 0 x 2 Total work done to move q 0 from A to B (from ∞ to r ) is B W∞B = r d. W = ∞ ∞ q q 0 4πε 0 x 2 dx =- q q 0 4πε 0 x 2 r ∞ 1 x 2 dx q W∞B = q 0 4πε 0 r q V = 4πε 0 r

Electric Potential due to a Group of Point Charges: The net electrostatic potential at a point in the electric field due to a group of charges is the algebraic sum of their individual potentials at that point. q 1 qn rn VP = V 1 + V 2 + V 3 + V 4 + …………+ Vn V= V= 1 4πε 0 n qi i=1 ri ∑ +1 C r 4 n qi i=1 │ r - ri │ ∑ r 1 q 2 r 2 P r 3 q 4 q 3 ( in terms of position vector ) 1. Electric potential at a point due to a charge is not affected by the presence of other charges. 2. Potential, V α 1 / r whereas Coulomb’s force F α 1 / r 2. 3. Potential is a scalar whereas Force is a vector. 4. Although V is called the potential at a point, it is actually equal to the potential difference between the points r and ∞.

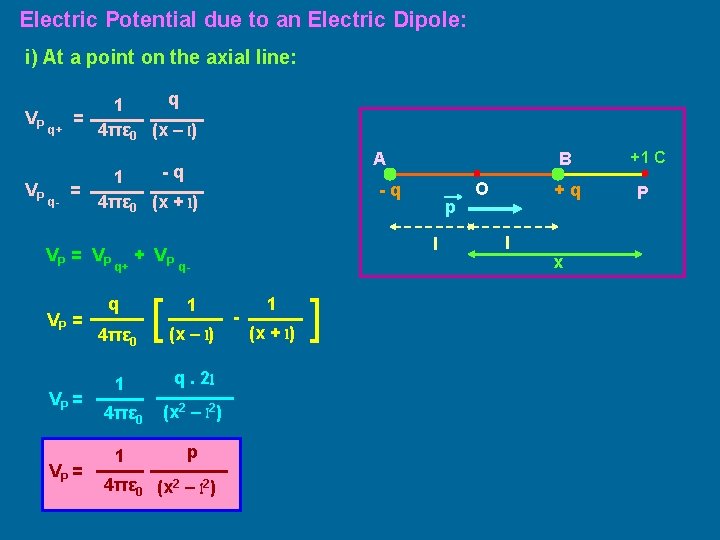
Electric Potential due to an Electric Dipole: i) At a point on the axial line: VP VP q+ q- q 1 = 4πε 0 (x – l) A -q 1 = 4πε 0 (x + l) V P = VP VP = q+ + VP q 4πε 0 [ B -q p l q- 1 (x – l) 1 q. 2 l 4πε 0 (x 2 – l 2) 1 p 4πε 0 (x 2 – l 2) - 1 (x + l) ] O +q l x +1 C P

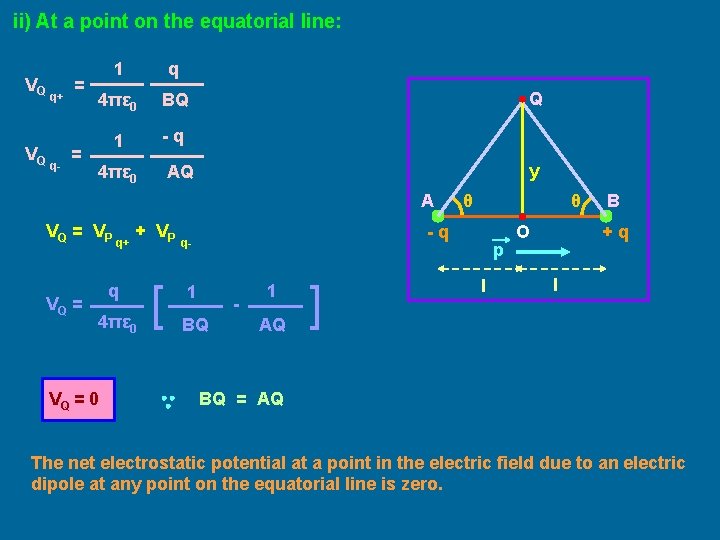
ii) At a point on the equatorial line: VQ VQ q+ q- = = 1 q 4πε 0 BQ 1 -q 4πε 0 Q y AQ A VQ = VP VQ = q+ + VP q 4πε 0 VQ = 0 [ θ θ -q q- 1 - BQ 1 AQ ] p l B +q O l BQ = AQ The net electrostatic potential at a point in the electric field due to an electric dipole at any point on the equatorial line is zero.

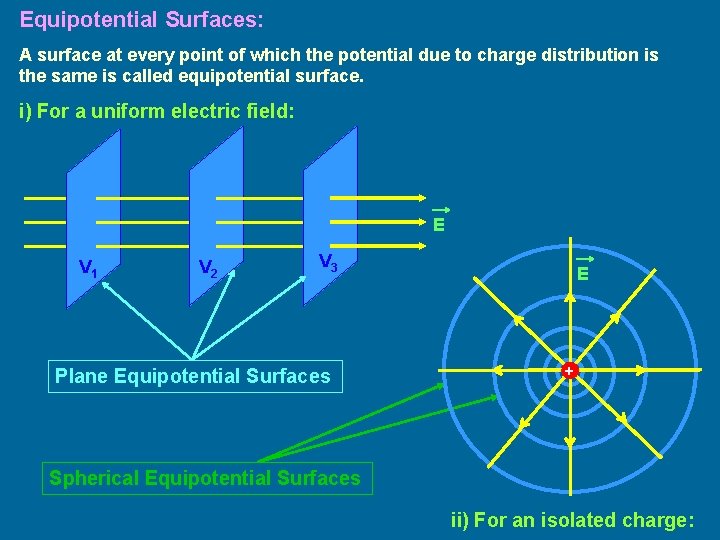
Equipotential Surfaces: A surface at every point of which the potential due to charge distribution is the same is called equipotential surface. i) For a uniform electric field: E V 1 V 2 V 3 Plane Equipotential Surfaces E + Spherical Equipotential Surfaces ii) For an isolated charge:

Properties of Equipotential Surfaces: 1. No work is done in moving a test charge from one point to another on an equipotential surface. WAB VB - VA = ∆V = q 0 If A and B are two points on the equipotential surface, then VB = VA. WAB =0 q 0 or WAB = 0 2. The electric field is always perpendicular to the element dl of the equipotential surface. Since no work is done on equipotential surface, B E. dl = 0 WAB = - i. e. E dl cos θ = 0 A As E ≠ 0 and dl ≠ 0, cos θ = 0 or θ = 90°

3. Equipotential surfaces indicate regions of strong or weak electric fields. Electric field is defined as the negative potential gradient. d. V E=dr or dr = - d. V E Since d. V is constant on equipotential surface, so dr α 1 E If E is strong (large), dr will be small, i. e. the separation of equipotential surfaces will be smaller (i. e. equipotential surfaces are crowded) and vice versa. 4. Two equipotential surfaces can not intersect. 5. If two equipotential surfaces intersect, then at the points of intersection, there will be two values of the electric potential which is not possible. 6. Note: (Refer to properties of electric lines of force) Electric potential is a scalar quantity whereas potential gradient is a vector quantity. The negative sign of potential gradient shows that the rate of change of potential with distance is always against the electric field intensity.

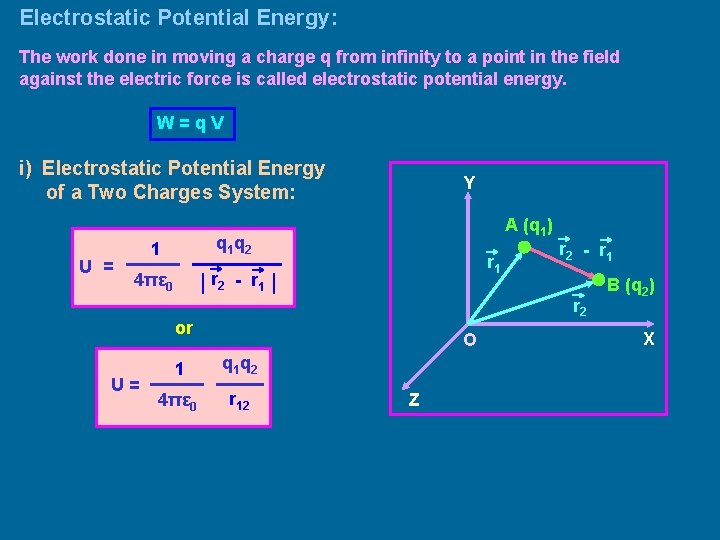
Electrostatic Potential Energy: The work done in moving a charge q from infinity to a point in the field against the electric force is called electrostatic potential energy. W=q. V i) Electrostatic Potential Energy of a Two Charges System: U = Y A (q 1) q 1 q 2 1 r 1 │ r 2 - r 1 │ 4πε 0 r 2 or U= r 2 - r 1 O 1 q 2 4πε 0 r 12 Z B (q 2) X

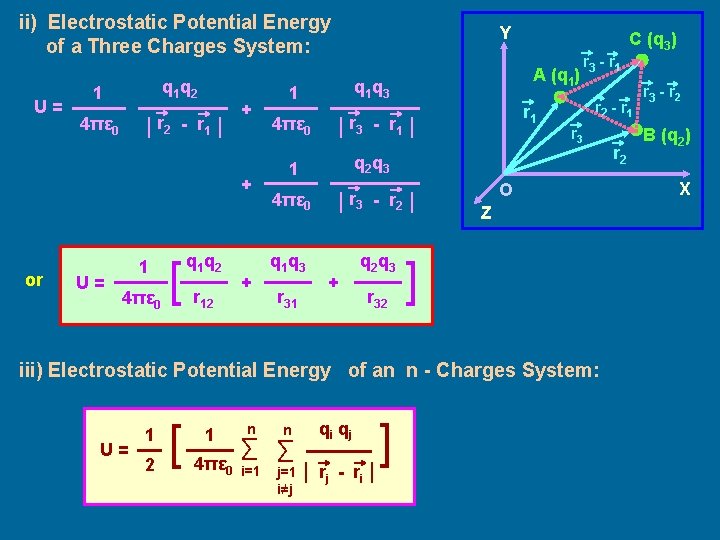
ii) Electrostatic Potential Energy of a Three Charges System: U= q 1 q 2 1 │ r 2 - r 1 │ 4πε 0 + + or U= 1 4πε 0 [ q 1 q 2 r 12 + Y A (q 1) q 1 q 3 1 r 3 - r 1 r 2 - r 1 r 3 q 2 q 3 1 4πε 0 │ r 3 - r 2 │ q 1 q 3 q 2 q 3 r 31 r 1 │ r 3 - r 1 │ 4πε 0 C (q 3) + r 32 O Z ] iii) Electrostatic Potential Energy of an n - Charges System: U= 1 2 [ 1 4πε 0 n n ∑ ∑ i=1 qi qj j=1 │ rj i≠j - ri │ ] r 2 r 3 - r 2 B (q 2) X

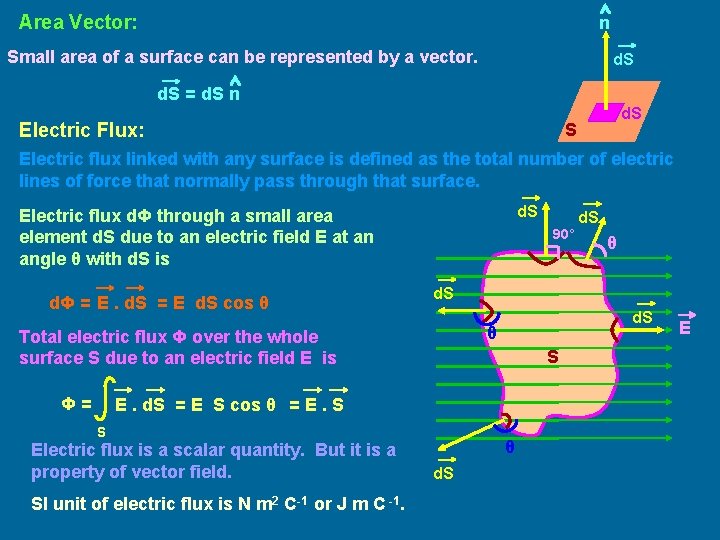
Area Vector: n Small area of a surface can be represented by a vector. d. S = d. S n Electric Flux: d. S S Electric flux linked with any surface is defined as the total number of electric lines of force that normally pass through that surface. d. S Electric flux dΦ through a small area element d. S due to an electric field E at an angle θ with d. S is dΦ = E. d. S = E d. S cos θ 90° d. S θ S E. d. S = E S cos θ = E. S S Electric flux is a scalar quantity. But it is a property of vector field. SI unit of electric flux is N m 2 C-1 or J m C -1. θ d. S Total electric flux Φ over the whole surface S due to an electric field E is Φ= d. S θ d. S E

Special Cases: 1. For 0° < θ < 90°, Φ is positive. 2. For θ = 90°, Φ is zero. 3. For 90° < θ < 180°, Φ is negative. Solid Angle: Solid angle is the three-dimensional equivalent of an ordinary twodimensional plane angle. SI unit of solid angle is steradian. r Solid angle subtended by area element d. S at the centre O of a sphere of radius r is θ d. S cos θ dΩ = d. S cos θ Ω = dΩ = S S d. S r 2 r = 4π steradian dΩ n

Gauss’s Theorem: The surface integral of the electric field intensity over any closed hypothetical surface (called Gaussian surface) in free space is equal to 1 / ε 0 times the net charge enclosed within the surface. n 1 ΦE = E. d. S = ε 0 S ∑ qi i=1 Proof of Gauss’s Theorem for Spherically Symmetric Surfaces: dΦ = E. d. S = dΦ = Here, 1 q 4πε 0 r 2 1 q d. S 4πε 0 r 2 r. d. S n E r r. n O • +q r r. n = 1 x 1 cos 0° = 1 dΦ = ΦE = 1 q d. S 4πε 0 r 2 1 q 4πε 0 r 2 dΦ = S d. S 1 q 4πε 0 r 2 4π r 2 = q ε 0

Proof of Gauss’s Theorem for a Closed Surface of any Shape: dΦ = E. d. S = dΦ = 1 q 4πε 0 r 2 1 q d. S 4πε 0 r 2 E r. d. S n r θ r. n d. S r Here, r. n = 1 x 1 cos θ = cos θ dΩ +q • dΦ = ΦE = 4πε 0 dΦ = S d. S cos θ q r 2 q 4πε 0 dΩ = S q 4πε 0 4π = q ε 0 n

Deduction of Coulomb’s Law from Gauss’s Theorem: From Gauss’s law, q ΦE = E. d. S = E ε 0 S Since E and d. S are in the same direction, q ΦE = E d. S = d. S O • +q r ε 0 S or r q ε 0 S E x 4π r 2 = q ε 0 or E= q 4πε 0 r 2 If a charge q 0 is placed at a point where E is calculated, then qq 0 F= 4πε 0 r 2 which is Coulomb’s Law.

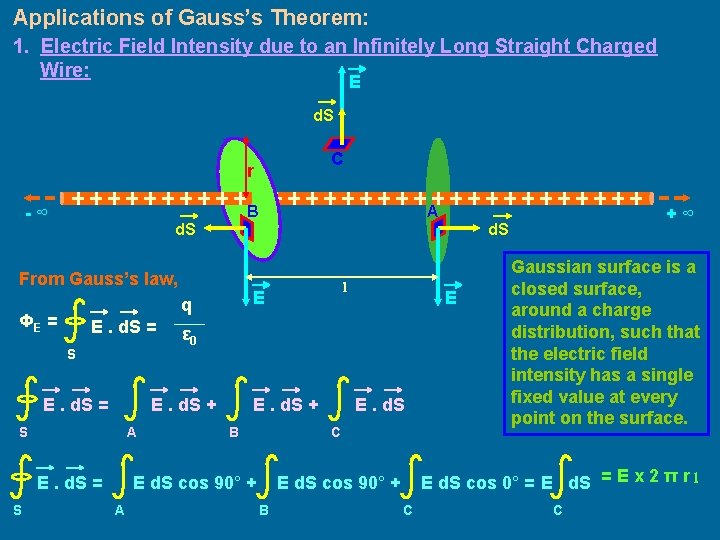
Applications of Gauss’s Theorem: 1. Electric Field Intensity due to an Infinitely Long Straight Charged Wire: E d. S C r B -∞ d. S E. d. S = A E. d. S = E. d. S + B E. d. S C E d. S cos 90° + A E ε 0 E. d. S + S l E q ΦE = +∞ d. S From Gauss’s law, S A E d. S cos 0° = E d. S = E x 2 π r l E d. S cos 90° + B Gaussian surface is a closed surface, around a charge distribution, such that the electric field intensity has a single fixed value at every point on the surface. C C

q ε 0 = λl (where λ is the liner charge density) ε 0 λl Ex 2πrl= ε 0 or 1 E= 2 πε 0 λ r or 1 E= 4 πε 0 2λ r In vector form, 1 E (r) = 4 πε 0 2λ r r The direction of the electric field intensity is radially outward from the positive line charge. For negative line charge, it will be radially inward. Note: The electric field intensity is independent of the size of the Gaussian surface constructed. It depends only on the distance of point of consideration. i. e. the Gaussian surface should contain the point of consideration.

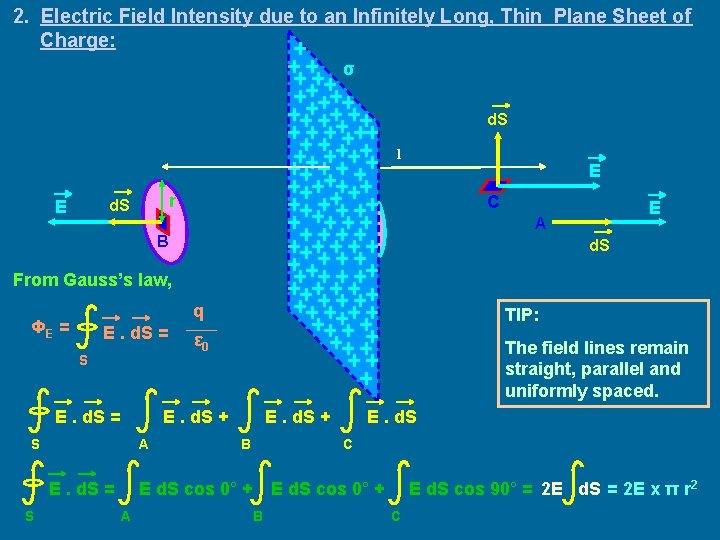
2. Electric Field Intensity due to an Infinitely Long, Thin Plane Sheet of Charge: σ d. S l r d. S E E C E A B d. S From Gauss’s law, ΦE = E. d. S = S E. d. S = TIP: ε 0 The field lines remain straight, parallel and uniformly spaced. E. d. S + S A E. d. S = S q E. d. S + B C E d. S cos 0° + A E. d. S E d. S cos 90° = 2 E d. S = 2 E x π r 2 E d. S cos 0° + B C

q ε 0 σ π r 2 = ε 0 2 Exπ or E= r 2 (where σ is the surface charge density) σ π r 2 = ε 0 σ 2 ε 0 In vector form, E (l) = σ 2 ε 0 l The direction of the electric field intensity is normal to the plane and away from the positive charge distribution. For negative charge distribution, it will be towards the plane. Note: The electric field intensity is independent of the size of the Gaussian surface constructed. It neither depends on the distance of point of consideration nor the radius of the cylindrical surface. If the plane sheet is thick, then the charge distribution will be available on both the sides. So, the charge enclosed within the Gaussian surface will be twice as before. Therefore, the field will be twice. E= σ ε 0

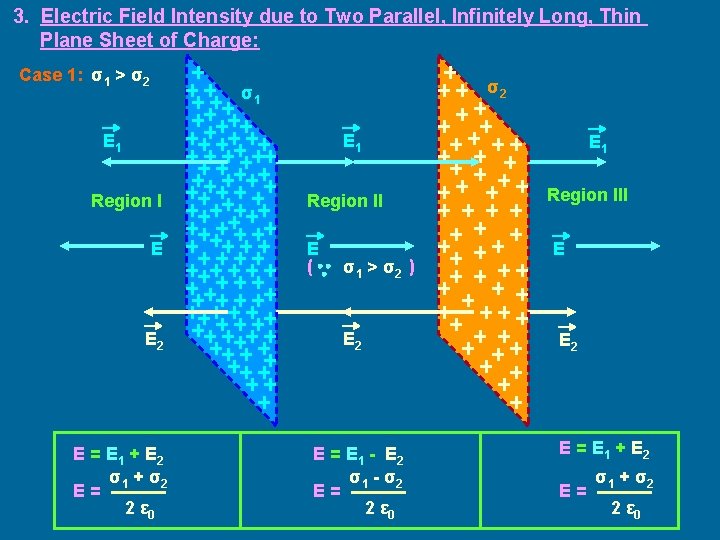
3. Electric Field Intensity due to Two Parallel, Infinitely Long, Thin Plane Sheet of Charge: Case 1: σ1 > σ2 σ2 σ1 E 1 Region I E E 2 E = E 1 + E 2 σ1 + σ2 E= 2 ε 0 Region II E ( σ1 > σ2 ) E 2 E = E 1 - E 2 σ1 - σ2 E= 2 ε 0 E 1 Region III E E 2 E = E 1 + E 2 E= σ1 + σ2 2 ε 0

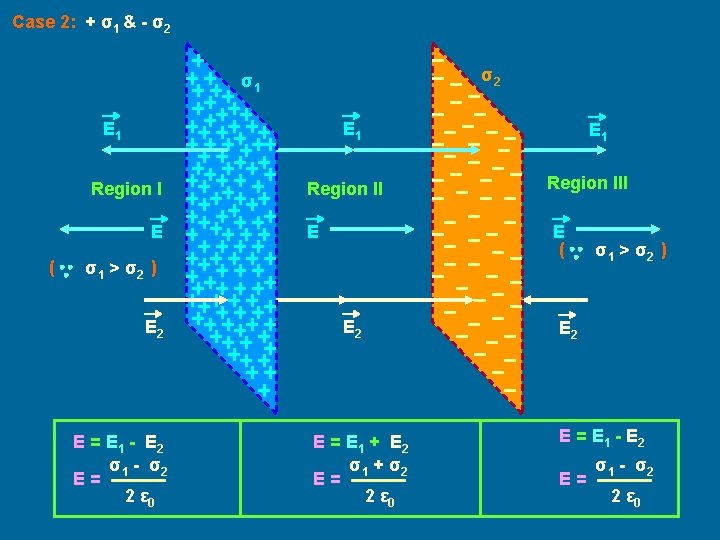
Case 2: + σ1 & - σ2 σ2 σ1 E 1 Region I E ( Region II E E = E 1 - E 2 σ1 - σ2 E= 2 ε 0 Region III E ( σ1 > σ2 ) E 2 E 1 E 2 E = E 1 + E 2 σ1 + σ2 E= 2 ε 0 σ1 > σ2 ) E 2 E = E 1 - E 2 E= σ1 - σ2 2 ε 0

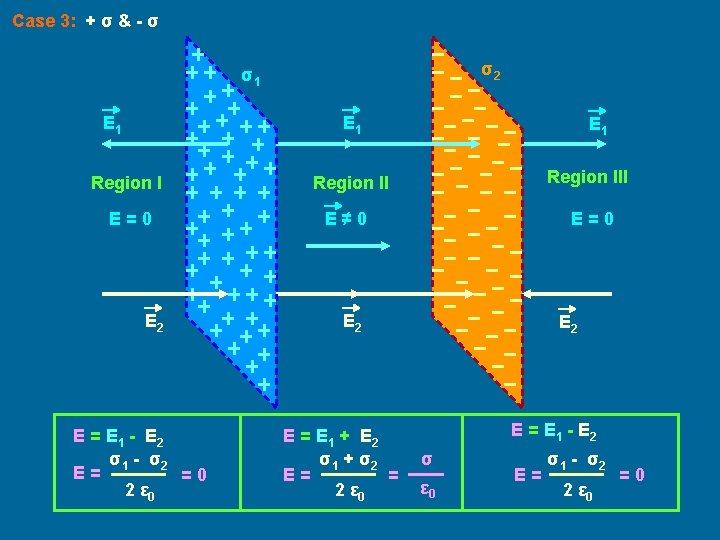
Case 3: + σ & - σ σ2 σ1 E 1 E 1 Region III E=0 E≠ 0 E=0 E 2 E = E 1 - E 2 σ1 - σ2 E= =0 2 ε 0 E 2 E = E 1 + E 2 σ1 + σ2 E= = 2 ε 0 E 2 E = E 1 - E 2 σ ε 0 E= σ1 - σ2 2 ε 0 =0

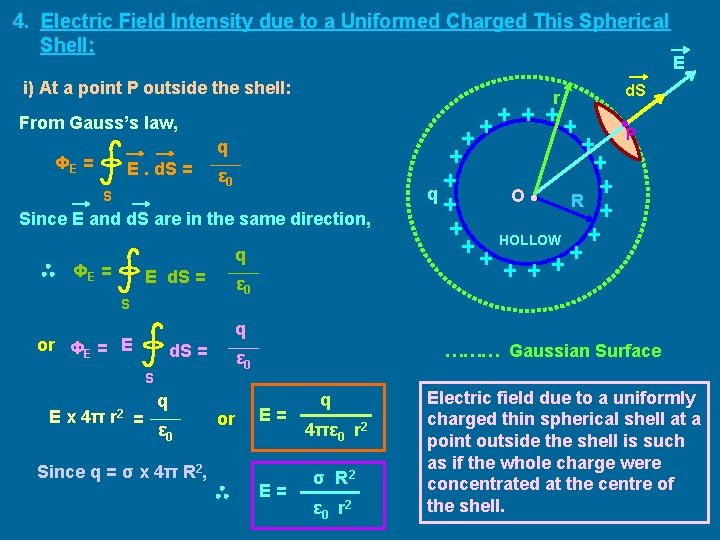
4. Electric Field Intensity due to a Uniformed Charged This Spherical Shell: i) At a point P outside the shell: d. S r • P From Gauss’s law, q ΦE = E. d. S = S ε 0 q Since E and d. S are in the same direction, E d. S = R ε 0 S q or ΦE = E d. S = q ε 0 Since q = σ x 4π R 2, ……… Gaussian Surface ε 0 S E x 4π r 2 = O • HOLLOW q ΦE = E or E= E= q 4πε 0 r 2 σ R 2 ε 0 r 2 Electric field due to a uniformly charged thin spherical shell at a point outside the shell is such as if the whole charge were concentrated at the centre of the shell.

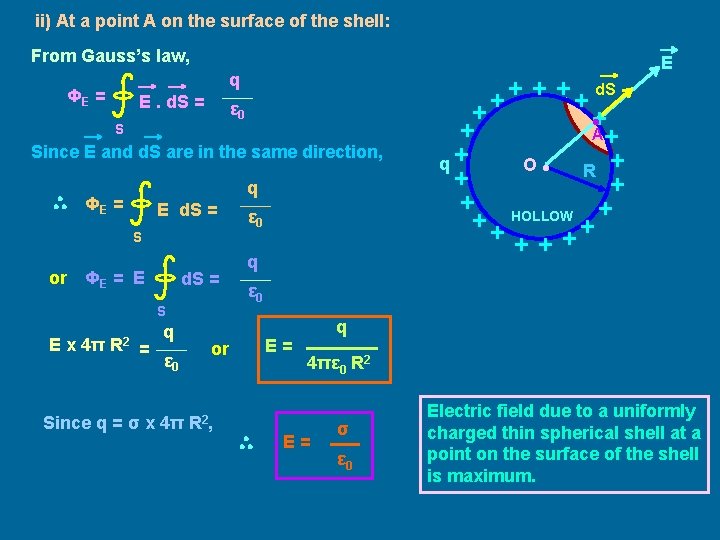
ii) At a point A on the surface of the shell: From Gauss’s law, E q ΦE = E. d. S = d. S ε 0 S • Since E and d. S are in the same direction, q ΦE = E d. S = S or ΦE = E d. S = S E x 4π R 2 = q ε 0 or Since q = σ x 4π R 2, ε 0 A q O • R HOLLOW q ε 0 E= q 4πε 0 R 2 E= σ ε 0 Electric field due to a uniformly charged thin spherical shell at a point on the surface of the shell is maximum.

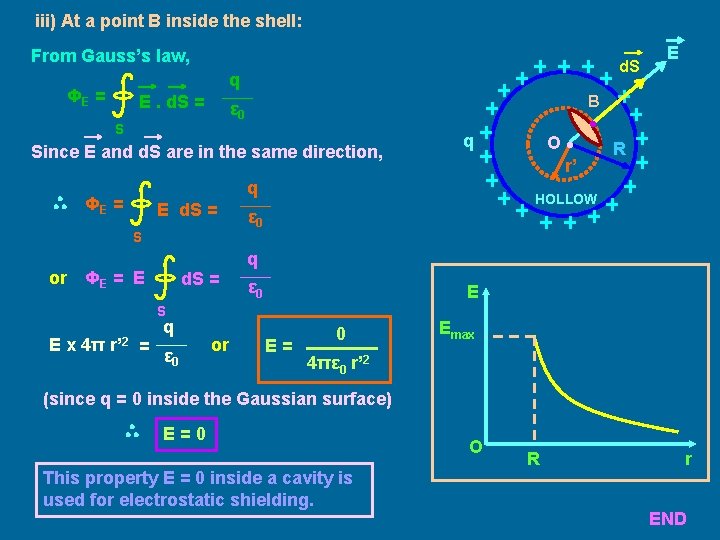
iii) At a point B inside the shell: From Gauss’s law, d. S q ΦE = E. d. S = B ε 0 S Since E and d. S are in the same direction, E d. S = S or = R HOLLOW ε 0 d. S = ε 0 E S E x 4π O • r’ • q ΦE = E r’ 2 q q ΦE = E q ε 0 or E= 0 Emax 4πε 0 r’ 2 (since q = 0 inside the Gaussian surface) E=0 This property E = 0 inside a cavity is used for electrostatic shielding. O R r END