Electrostatics Electric Potential Energy Electrical Potential Energy FE

Electrostatics Electric Potential Energy

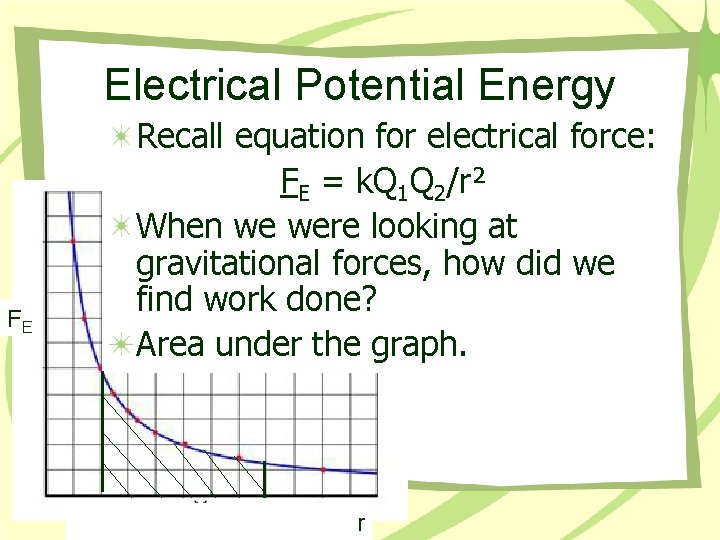
Electrical Potential Energy FE Recall equation for electrical force: FE = k. Q 1 Q 2/r² When we were looking at gravitational forces, how did we find work done? Area under the graph. r

Electrical Potential Energy EP = k. Q 1 Q 2/r When using the potential energy equation, keep the following in mind: Amount of potential energy due to separation of two charged particles by distance “r”. Include the signs of the charged particles Drop the -’ve sign

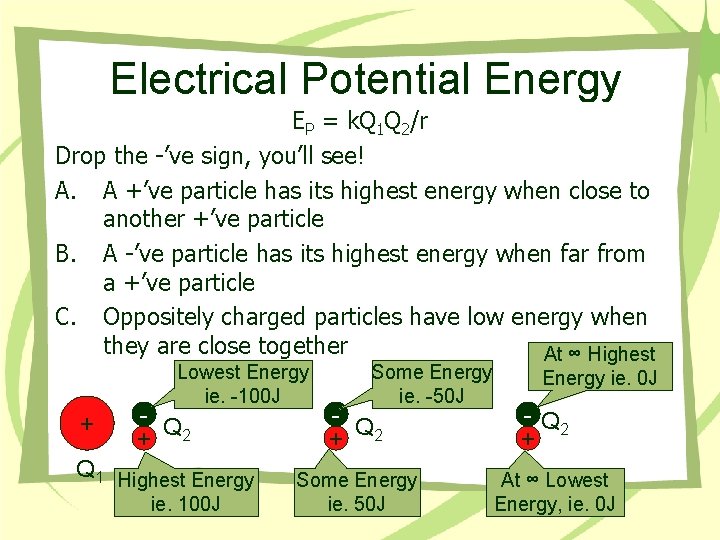
Electrical Potential Energy EP = k. Q 1 Q 2/r Drop the -’ve sign, you’ll see! A. A +’ve particle has its highest energy when close to another +’ve particle B. A -’ve particle has its highest energy when far from a +’ve particle C. Oppositely charged particles have low energy when they are close together At ∞ Highest Lowest Energy ie. -100 J + - Q + 2 Q 1 Highest Energy ie. 100 J Some Energy ie. -50 J - Q + 2 Some Energy ie. 50 J Energy ie. 0 J - Q 2 + At ∞ Lowest Energy, ie. 0 J

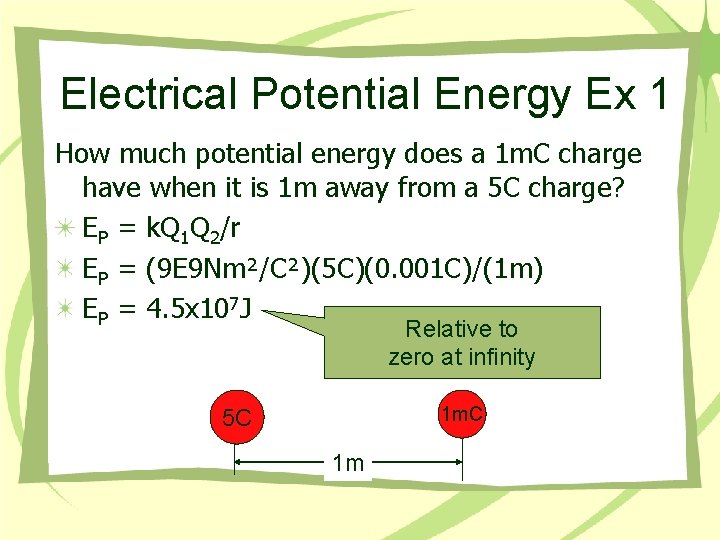
Electrical Potential Energy Ex 1 How much potential energy does a 1 m. C charge have when it is 1 m away from a 5 C charge? EP = k. Q 1 Q 2/r EP = (9 E 9 Nm²/C²)(5 C)(0. 001 C)/(1 m) EP = 4. 5 x 107 J Relative to zero at infinity 1 m. C 5 C 1 m

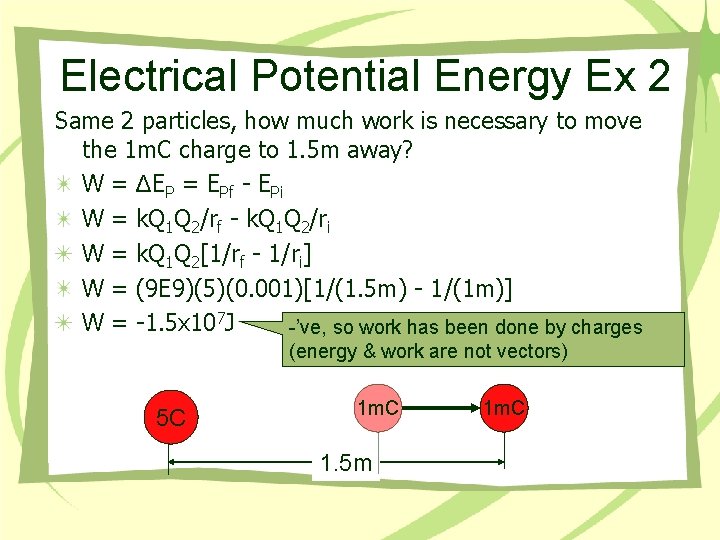
Electrical Potential Energy Ex 2 Same 2 particles, how much work is necessary to move the 1 m. C charge to 1. 5 m away? W = ΔEP = EPf - EPi W = k. Q 1 Q 2/rf - k. Q 1 Q 2/ri W = k. Q 1 Q 2[1/rf - 1/ri] W = (9 E 9)(5)(0. 001)[1/(1. 5 m) - 1/(1 m)] W = -1. 5 x 107 J -’ve, so work has been done by charges (energy & work are not vectors) 5 C 1 m. C 1. 5 m 1 m. C

Conclusions Potential Energy: EP = k. Q 1 Q 2/r Like charges experience a +’ve potential energy that increase the closer they are together Dislike charges experience a -’ve potential energy that decreases the closer they are together Particles experience zero potential energy when they are infinitely far apart from one another

Electrostatics Electric Potential Voltage

Electrical Potential We have already looked at the amount of energy a charge has: E = k. Q 1 Q 2/r But that is rarely useful, let’s look at the total amount of energy a charge has: ELECTRIC POTENTIAL

Electrical Potential Electric Potential is also sometimes called just simply “Potential” Symbol is “V” (Named after Volta) Measured in Volts (J/C) It is the amount of work required to move a unit of charge from point A to point B V = EP/q V = (k. Qq/r) / q V = k. Q/r Alessandro Volta - Built the first battery

Electrical Potential Example: Find potential of the -5 m. C charge at 1. 5 m and at 5 m away? V = k. Q/r V 1. 5 = (9 E 9 J)(-0. 005 C)/(1. 5 m) § V 1. 5 = -3 x 107 V V 5 = (9 E 9 J)(-0. 005 C)/(5 m) § V 5 = -9 x 106 V -5 m. C V 1. 5 m V 5 5 m

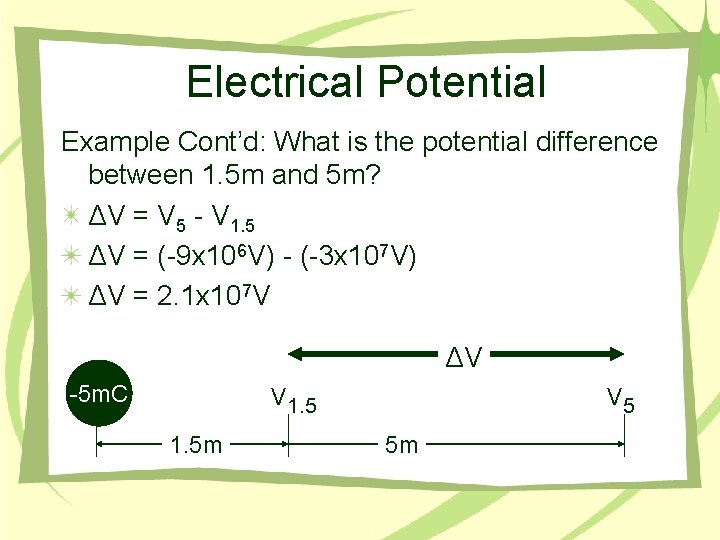
Electrical Potential Example Cont’d: What is the potential difference between 1. 5 m and 5 m? ΔV = V 5 - V 1. 5 ΔV = (-9 x 106 V) - (-3 x 107 V) ΔV = 2. 1 x 107 V ΔV -5 m. C V 1. 5 m V 5 5 m

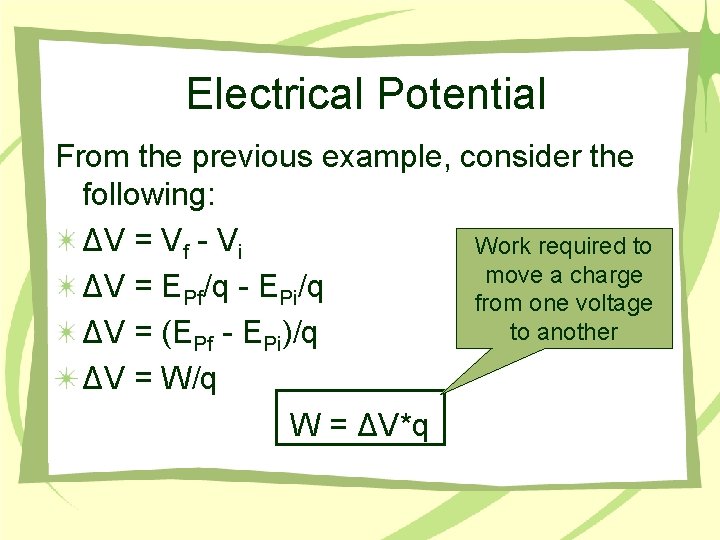
Electrical Potential From the previous example, consider the following: ΔV = Vf - Vi Work required to move a charge ΔV = EPf/q - EPi/q from one voltage to another ΔV = (EPf - EPi)/q ΔV = W/q W = ΔV*q

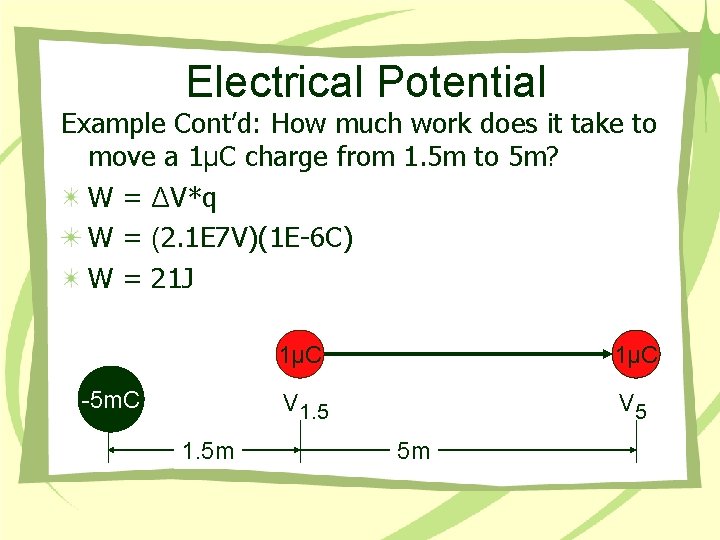
Electrical Potential Example Cont’d: How much work does it take to move a 1μC charge from 1. 5 m to 5 m? W = ΔV*q W = (2. 1 E 7 V)(1 E-6 C) W = 21 J -5 m. C 1. 5 m 1μC V 1. 5 V 5 5 m

Conclusions Electric Potential, Voltage Same Diff Measured in Volts V = k. Q/r W = ΔV*q Zero volts is sometimes called ground Symbol is