Electrostatics 3 The Electric Field HW 2 last

Electrostatics #3 The Electric Field HW #2, last page of handout

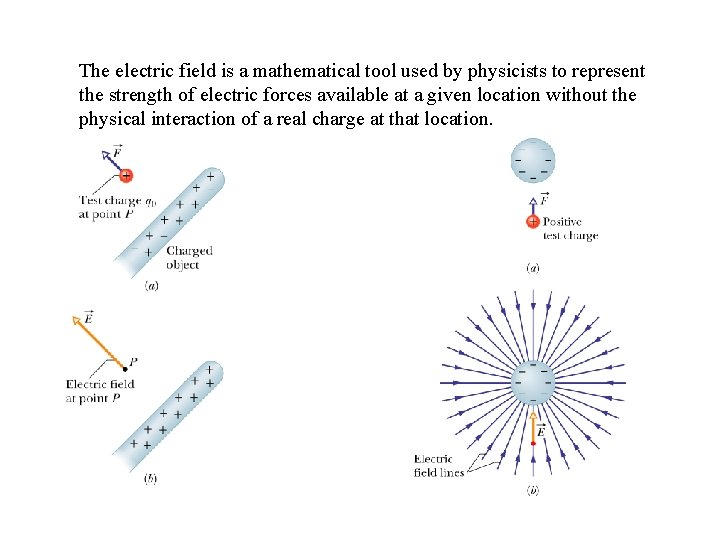
I. Electric Field: Day #1 Introduction: When scientists try to study an unknown arrangement of charges, the only tool available is to place a test charge near the distribution and measure the force on the test charge. The downside to this technique is that the test charge might cause a change to the distribution of charge. A test charge is placed near an object to measure the force on the test charge. Example of how the presence of a test charge may change the distribution of the charges in the original object.

The electric field is a mathematical tool used by physicists to represent the strength of electric forces available at a given location without the physical interaction of a real charge at that location.

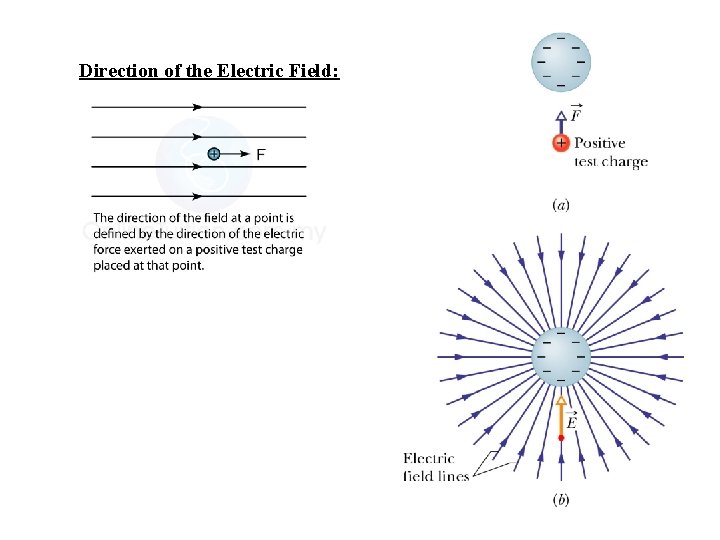
An imaginary positive test charge, q, is placed at some location near a distribution of charge. A force F would be exerted on this test charge. The electric field measures the force available at that point in space, but represents it as the force per unit charge. In other words: Units for the electric field: force per charge =

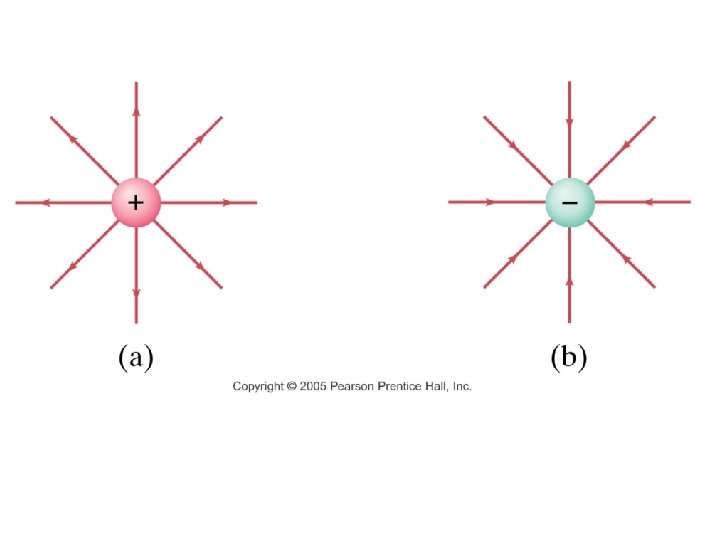
Point Charges as Sources of Electric Fields: The electric field created by a point charge (or spherical distribution of charge) will point radially outwards from or inwards towards the charge.

Direction of the Electric Field:

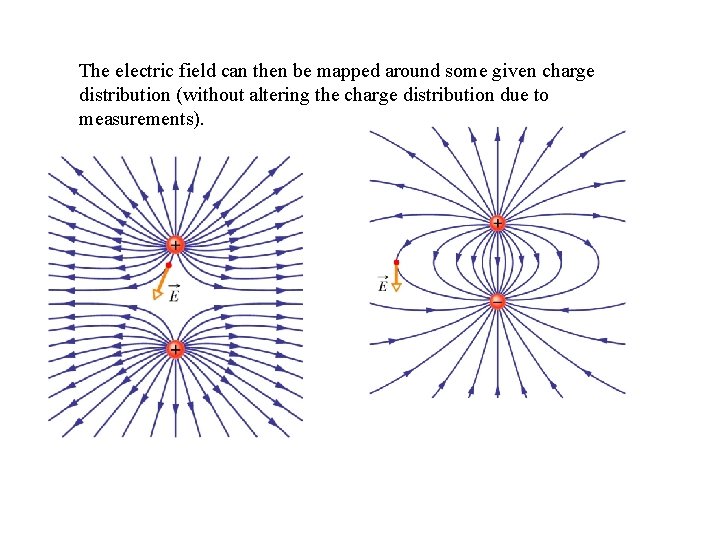
The electric field can then be mapped around some given charge distribution (without altering the charge distribution due to measurements).

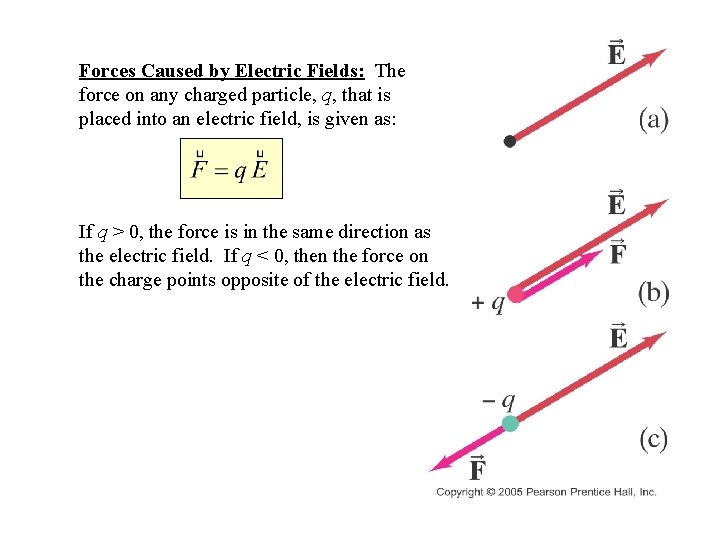
Forces Caused by Electric Fields: The force on any charged particle, q, that is placed into an electric field, is given as: If q > 0, the force is in the same direction as the electric field. If q < 0, then the force on the charge points opposite of the electric field.

The strength of the electric field around a point charge is given as follows: The force on the positive test charge, qo, is given from Coulomb’s law. The strength of the electric field is found by dividing the force on the positive test charge, qo, by the value of the test charge: The electric field depends only on the properties of and the distance from the point charge, Q.

Electrostatics #3 The Electric Field 2 nd day towards this lesson

Electric Field: Day #2 Force on a test charge: Electric field due to a point source charge: {always true!}

Example #1: A point charge with a mass of 1. 40 kg and charge of +25. 0 m. C is placed into a constant electric field. a. If the strength of the electric field is 863 N/C pointing due north, what is the force on the charged particle? Since the charge interacting with the electric field is positive, the force also points north (same as the electric field).

b. If the particle starts from rest, how long will it take the particle to reach 15. 0 m/s?

Example #2: An object with a net charge of 24 μC is placed in a uniform electric field of 610 N/C, directed vertically. What is the mass of the object if it “floats” in the electric field? If the mass is to float, there must be an upward force to balance gravity! Note that if the charge is positive and the electric force points upwards, then the electric field must point upwards as well. Balance the forces:

Example #3: An electron is accelerated by a constant electric field of magnitude 300 N/C. (a) Find the acceleration of the electron. (b) Use the equations of motion with constant acceleration to find the electron’s speed after 1. 00 × 10− 8 s, assuming it starts from rest.

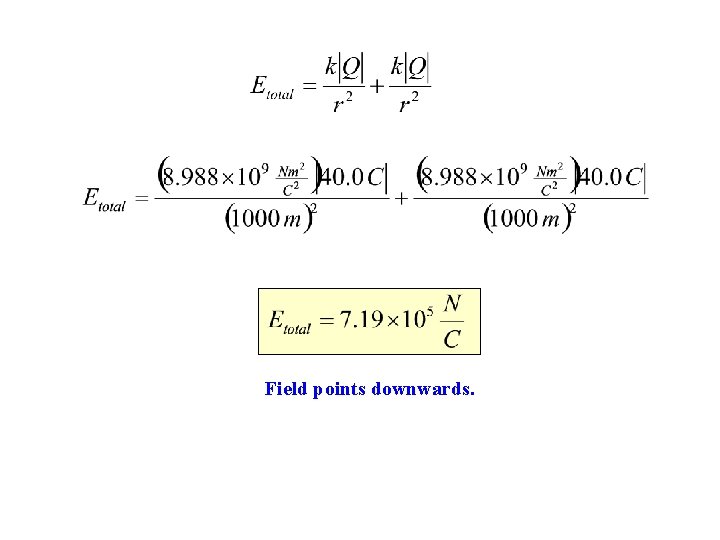
Example #4: An airplane is flying through a thundercloud at a height of 2000 m. (This is a very dangerous thing to do because of updrafts, turbulence, and the possibility of electric discharge. ) If there are charge concentrations of +40. 0 C at a height of 3000 m within the cloud and − 40. 0 C at a height of 1000 m, what is the electric field at the aircraft? Note that the airplane is 1000 m below the top charge and 1000 m above the bottom charge. Both electric fields point downwards.

Field points downwards.

Example #5: A proton accelerates from rest in a uniform electric field of 640 N/C. At some later time, its speed is 1. 20 × 106 m/s. (a) Find the magnitude of the acceleration of the proton.

Example #5: (b) How long does it take the proton to reach this speed?

Example #5: (c) How far has it moved in that interval?

Example #5: (d) What is its kinetic energy at the later time?

Example #6: Each of the protons in a particle beam has a kinetic energy of 3. 25 × 10− 15 J. What are the magnitude and direction of the electric field that will stop these protons in a distance of 1. 25 m?

The magnitude of the force is given as: Set this force equal to: Note that the force must point opposite to the motion to slow the proton down. Since this is a positive charge, the electric field will point the same direction as the force. The electric field thus points opposite to the motion of the positive charge.

For a positive charge, the electric field will point in the direction of motion in order to speed up the positive charge. To slow down a positive charge, the electric field must point opposite to the motion. For a negative charge, the electric field will point opposite to the direction of motion in order to speed up the negative charge. To slow down a negative charge, the electric field must point in the same direction as the motion.

Example #7: Each of the electrons in a particle beam has a kinetic energy of 1. 60 × 10− 17 J. (a) What is the magnitude of the uniform electric field (pointing in the direction of the electrons’ movement) that will stop these electrons in a distance of 10. 0 cm? (b) How long will it take to stop the electrons? (c) After the electrons stop, what will they do? Explain.

Note that the force must point opposite to the motion to slow the electron down. Since this is a negative charge, the electric field will point opposite to the direction of the force. Thus the electric field points in the direction the electron moves.

Example #7: {continued…} (b) How long will it take to stop the electrons? (c) After the electrons stop, what will they do? Explain. Even after the electrons stop, the acceleration is still present. The electrons will accelerate in the opposite direction. This is the same as throwing a ball in the air. The ball comes back down after stopping at the highest point.

Electrostatics #3 The Electric Field HW #3, #4, and Coulomb’s Law worksheet will be checked Tuesday.

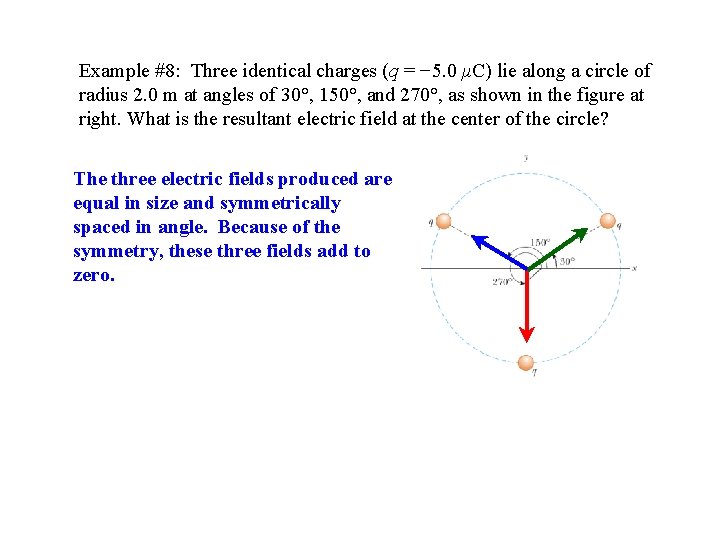
Example #8: Three identical charges (q = − 5. 0 μC) lie along a circle of radius 2. 0 m at angles of 30°, 150°, and 270°, as shown in the figure at right. What is the resultant electric field at the center of the circle? The three electric fields produced are equal in size and symmetrically spaced in angle. Because of the symmetry, these three fields add to zero.

Example #9: (a) Determine the electric field strength at a point 1. 00 cm to the left of the middle charge shown in the figure below. points right points left points right

Use (+) to indicate pointing right and (–) to indicate pointing left: points right (b) If a charge of − 2. 00 μC is placed at this point, what are the magnitude and direction of the force on it? points left The force on a negative charge is directed opposite to the electric field.

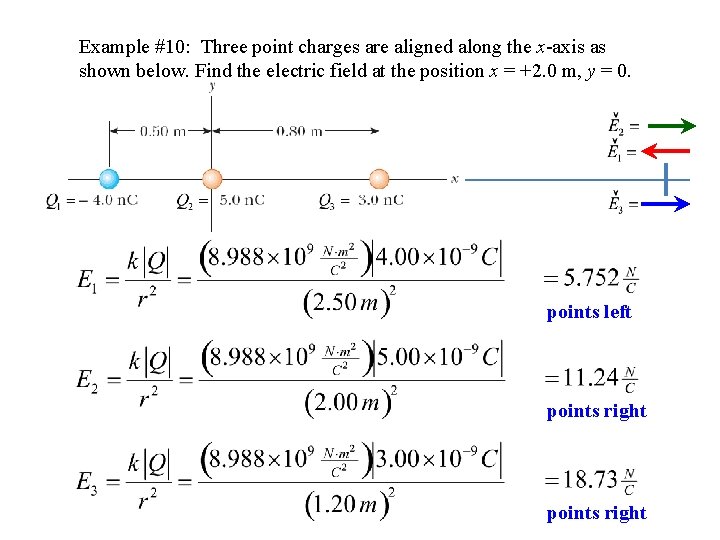
Example #10: Three point charges are aligned along the x-axis as shown below. Find the electric field at the position x = +2. 0 m, y = 0. points left points right

Use (+) to indicate pointing right and (–) to indicate pointing left: points right

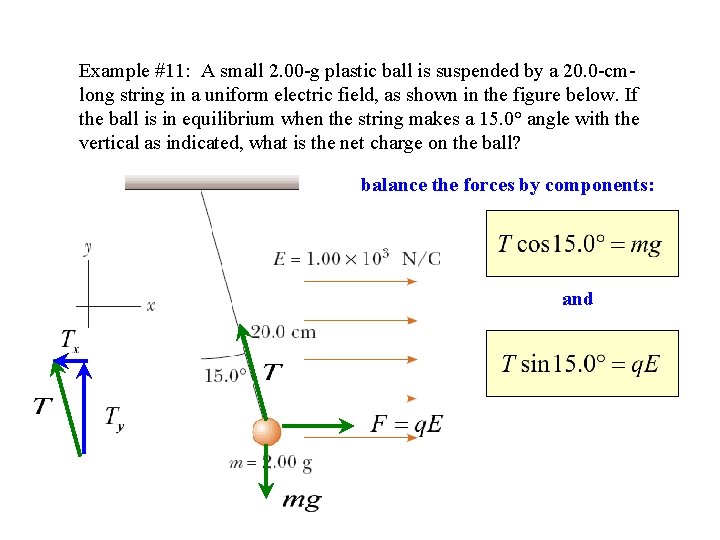
Example #11: A small 2. 00 -g plastic ball is suspended by a 20. 0 -cmlong string in a uniform electric field, as shown in the figure below. If the ball is in equilibrium when the string makes a 15. 0° angle with the vertical as indicated, what is the net charge on the ball? balance the forces by components: and

Divide the two force equations:

Example #12: A positively charged bead having a mass of 1. 00 g falls from rest in a vacuum from a height of 5. 00 m in a uniform vertical electric field with a magnitude of 1. 00 × 104 N/C. The bead hits the ground at a speed of 21. 0 m/s. Determine (a) the direction of the electric field (upward or downward), and (b) the charge on the bead. Start with kinematics to find the downward acceleration of the bead. the downward acceleration is greater than normal gravity, so an additional (electric) force is also pushing downwards on the bead. (a) The electric field must be pointing downwards to make a downward force on the positively charged bead.

take downwards as positive…

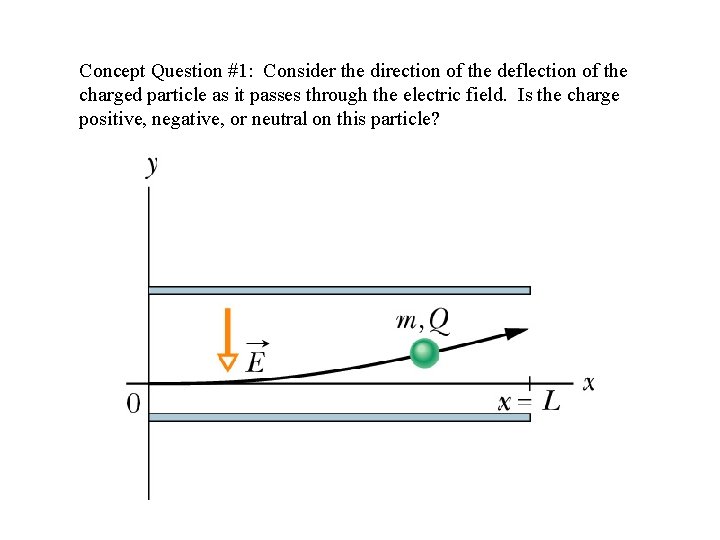
Concept Question #1: Consider the direction of the deflection of the charged particle as it passes through the electric field. Is the charge positive, negative, or neutral on this particle?

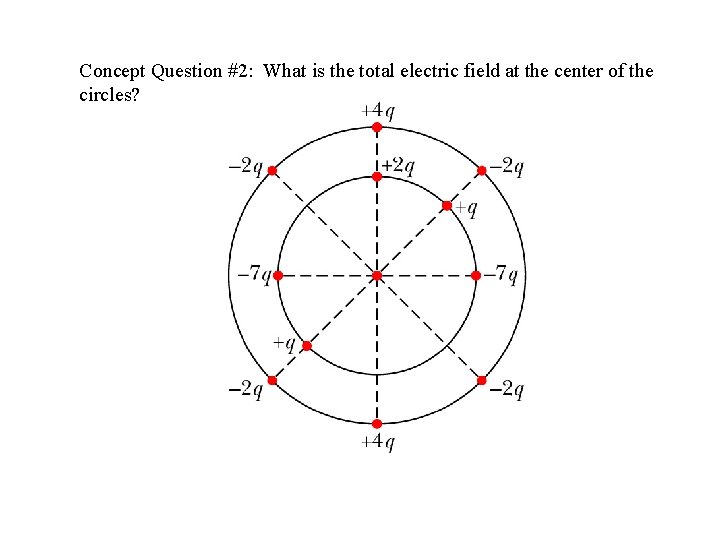
Concept Question #2: What is the total electric field at the center of the circles?

Concept Question #3: What is the total electric force on the charge at the center of the square?

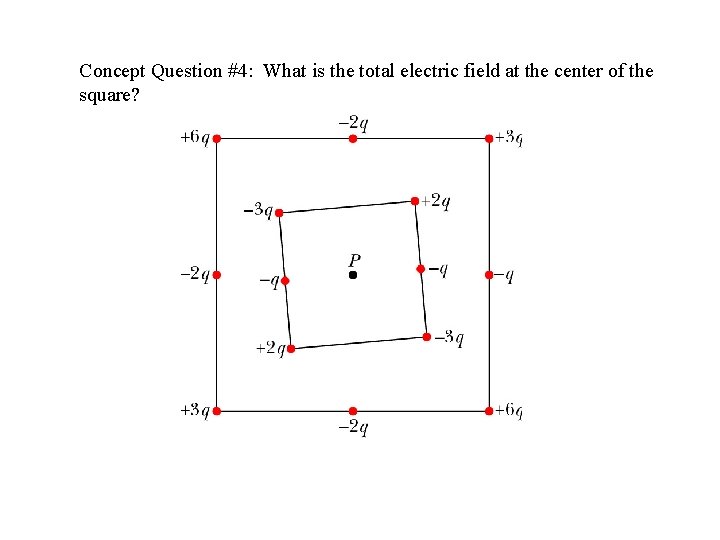
Concept Question #4: What is the total electric field at the center of the square?