Electronnuclear spin dynamics in optically pumped semiconductor quantum

Electron-nuclear spin dynamics in optically pumped semiconductor quantum dots K. V. Kavokin A. F. Ioffe Physico-Technical Institute, St. Petersburg, Russia Thanks to: Igor Merkulov, Vladimir Kalevich, Vladimir Korenev, Roslan Dzhioev (Ioffe Institute) Alexander Tartakovskii, Evgeniy Chekhovich, Maurice Skolnick (Sheffield) Thierry Amand, Xavier Marie, Bernhard Urbaszek (Toulouse)

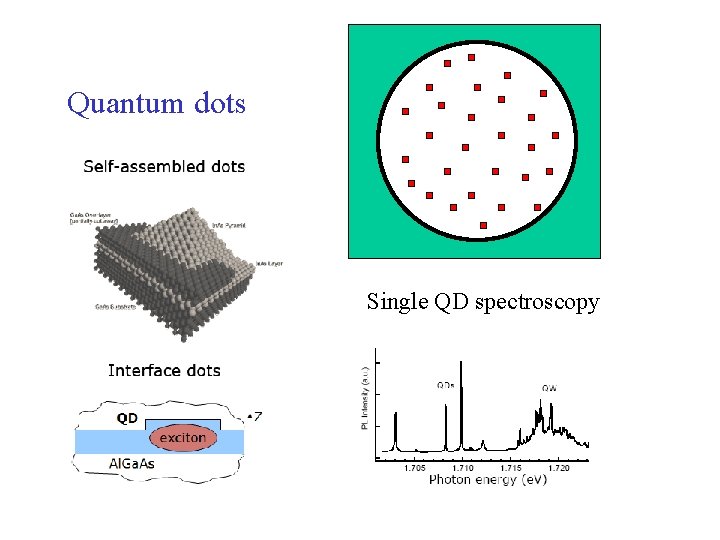
Quantum dots Single QD spectroscopy

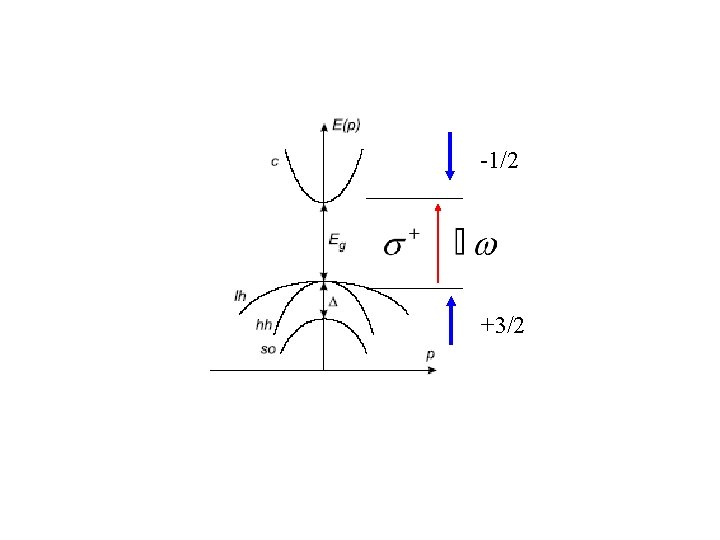
Electrons in conduction band: contact Fermi interaction Valence band holes: magnetic dipole interaction, much weaker

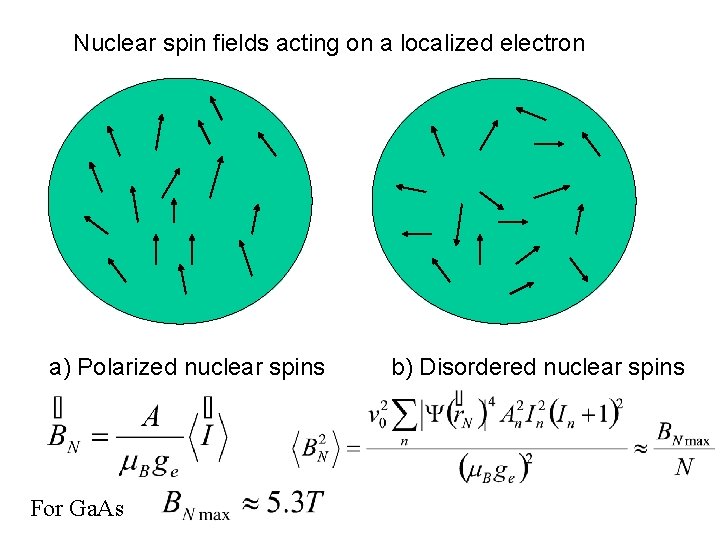
Nuclear spin fields acting on a localized electron a) Polarized nuclear spins For Ga. As b) Disordered nuclear spins

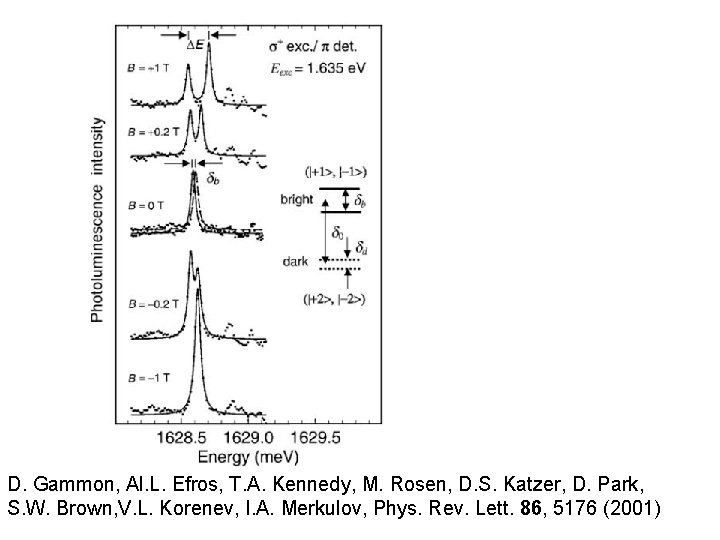
D. Gammon, Al. L. Efros, T. A. Kennedy, M. Rosen, D. S. Katzer, D. Park, S. W. Brown, V. L. Korenev, I. A. Merkulov, Phys. Rev. Lett. 86, 5176 (2001)

-1/2 +3/2

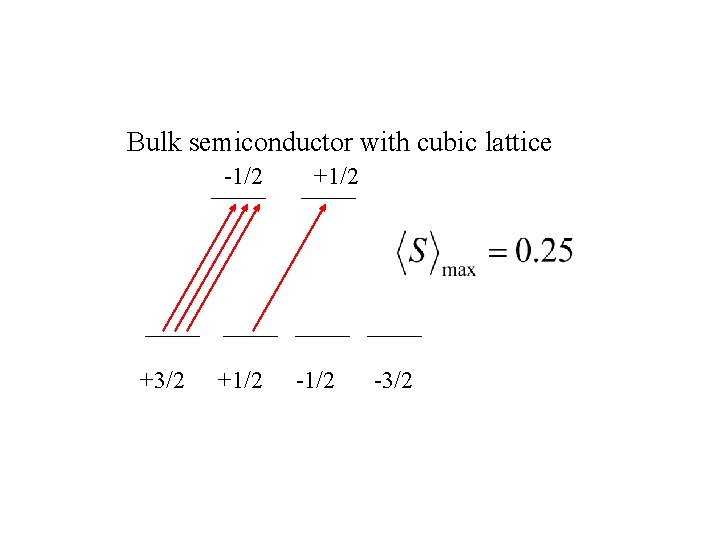
Bulk semiconductor with cubic lattice -1/2 +3/2 +1/2 -1/2 -3/2

Quantum wells, quantum dots -1/2 +3/2 -3/2 +1/2 -1/2

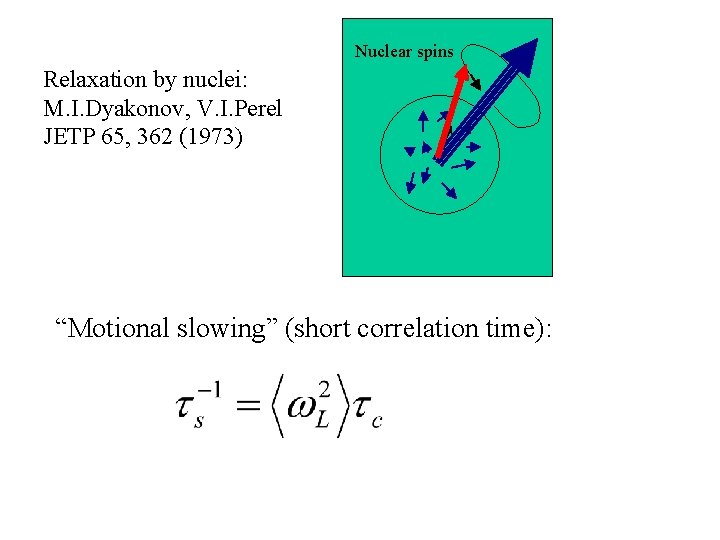
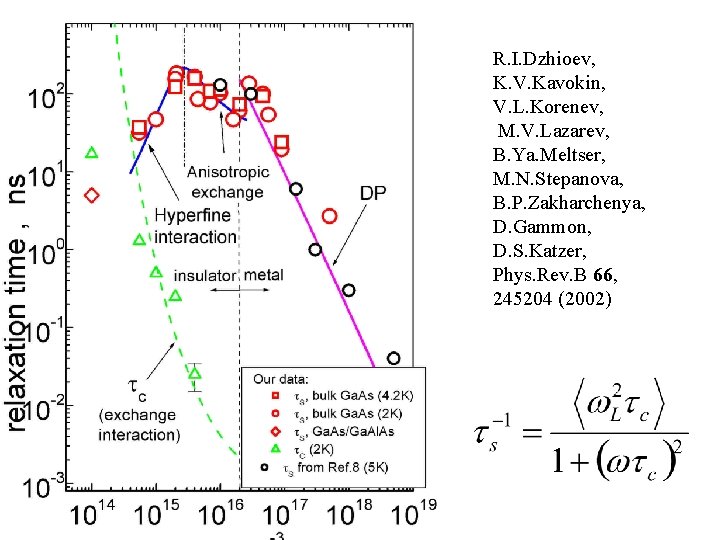
Nuclear spins Relaxation by nuclei: M. I. Dyakonov, V. I. Perel JETP 65, 362 (1973) “Motional slowing” (short correlation time):

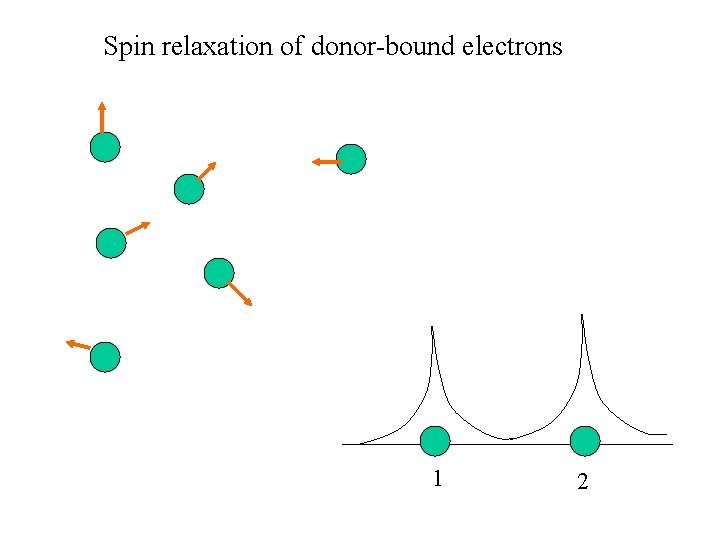
Spin relaxation of donor-bound electrons 1 2

R. I. Dzhioev, K. V. Kavokin, V. L. Korenev, M. V. Lazarev, B. Ya. Meltser, M. N. Stepanova, B. P. Zakharchenya, D. Gammon, D. S. Katzer, Phys. Rev. B 66, 245204 (2002)

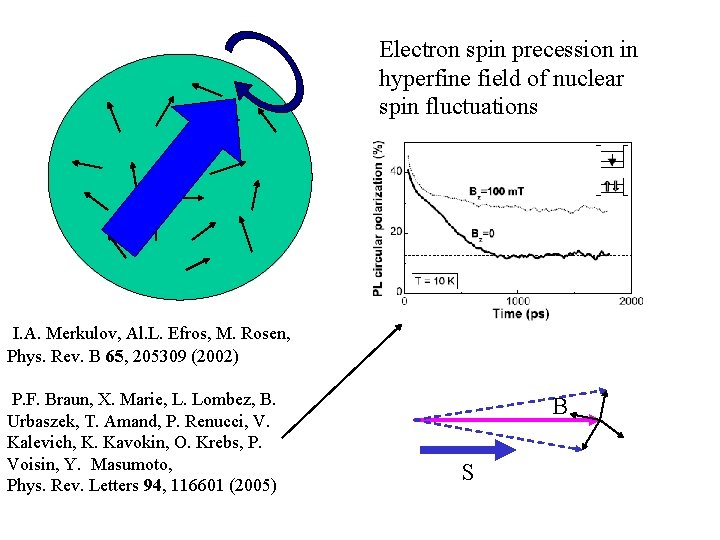
Electron spin precession in hyperfine field of nuclear spin fluctuations I. A. Merkulov, Al. L. Efros, M. Rosen, Phys. Rev. B 65, 205309 (2002) P. F. Braun, X. Marie, L. Lombez, B. Urbaszek, T. Amand, P. Renucci, V. Kalevich, K. Kavokin, O. Krebs, P. Voisin, Y. Masumoto, Phys. Rev. Letters 94, 116601 (2005) B S

Electrons in conduction band: contact Fermi interaction The total angular momentum is conserved!

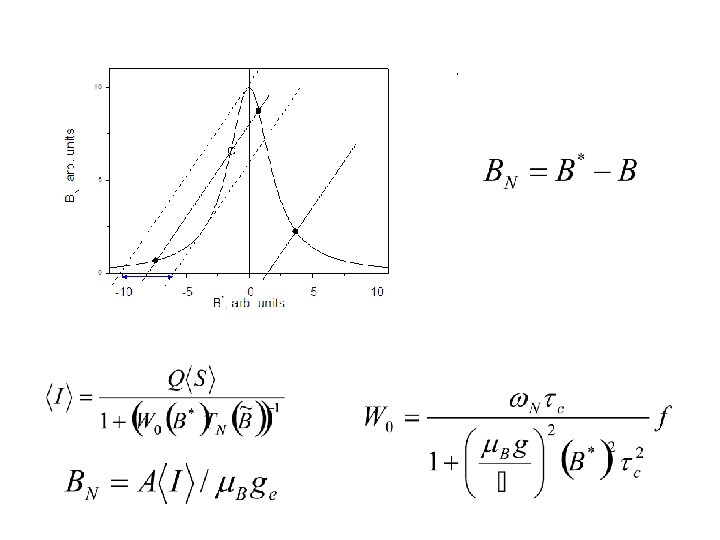
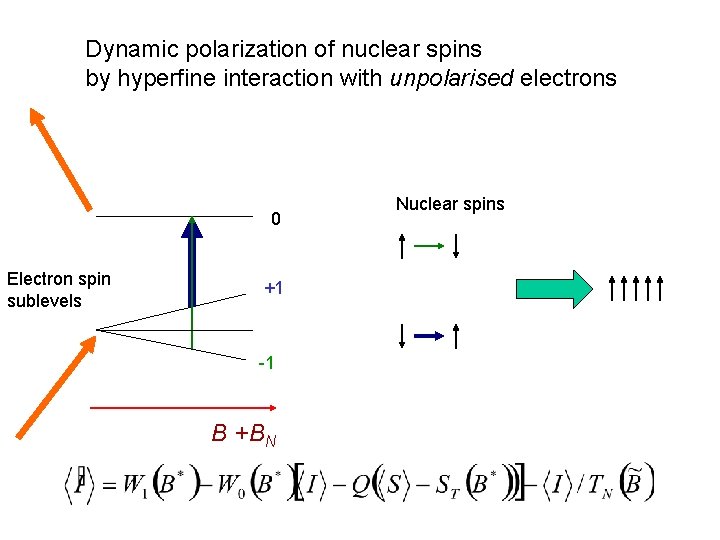
Dynamic polarization of nuclear spins by hyperfine interaction Spin influx into the nuclear spin system: R is the rate of a non-equilibrium process is a pseudovector changing sign under time inversion Optical orientation: If

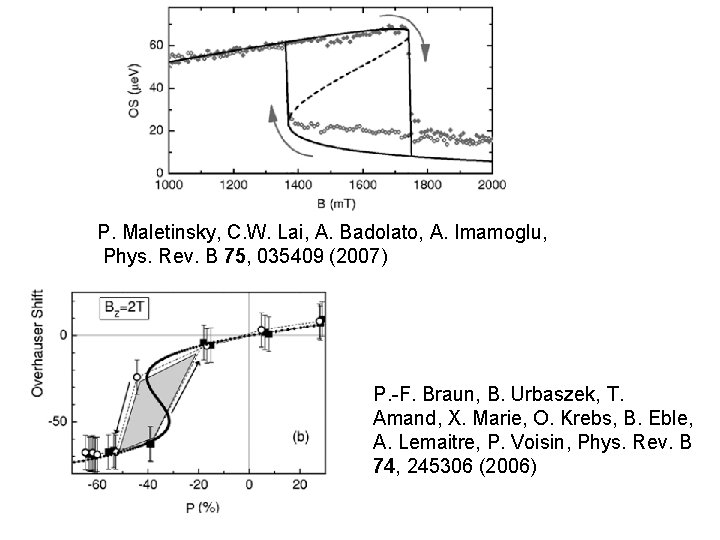
P. Maletinsky, C. W. Lai, A. Badolato, A. Imamoglu, Phys. Rev. B 75, 035409 (2007) P. -F. Braun, B. Urbaszek, T. Amand, X. Marie, O. Krebs, B. Eble, A. Lemaitre, P. Voisin, Phys. Rev. B 74, 245306 (2006)

Dynamic polarization of nuclear spins by hyperfine interaction with unpolarised electrons 0 Electron spin sublevels +1 -1 B +BN Nuclear spins

Pump

Pump

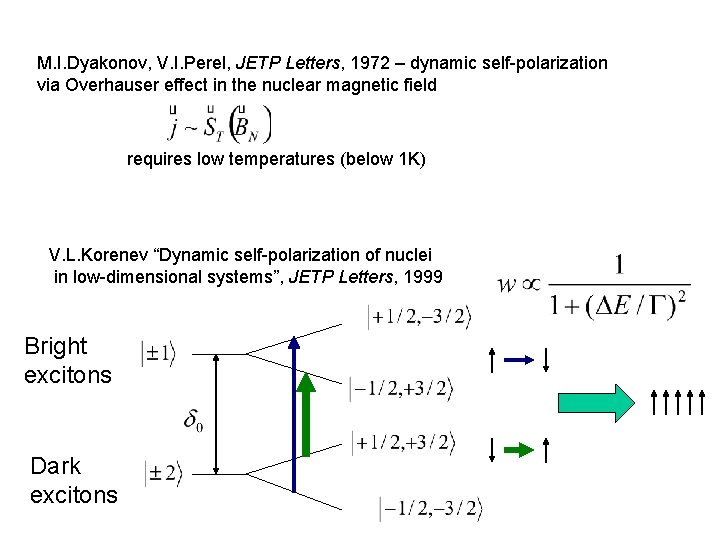
M. I. Dyakonov, V. I. Perel, JETP Letters, 1972 – dynamic self-polarization via Overhauser effect in the nuclear magnetic field requires low temperatures (below 1 K) V. L. Korenev “Dynamic self-polarization of nuclei in low-dimensional systems”, JETP Letters, 1999 Bright excitons Dark excitons

Why magnetic field is needed to polarize nuclei? Magnetic dipole-dipole interaction Local field BL B>>BL : TN=T 1, 103 s B~BL : TN=T 2 10 -4 s

When we polarize nuclear spins in a magnetic field, we change the energy of the nuclear spin system!

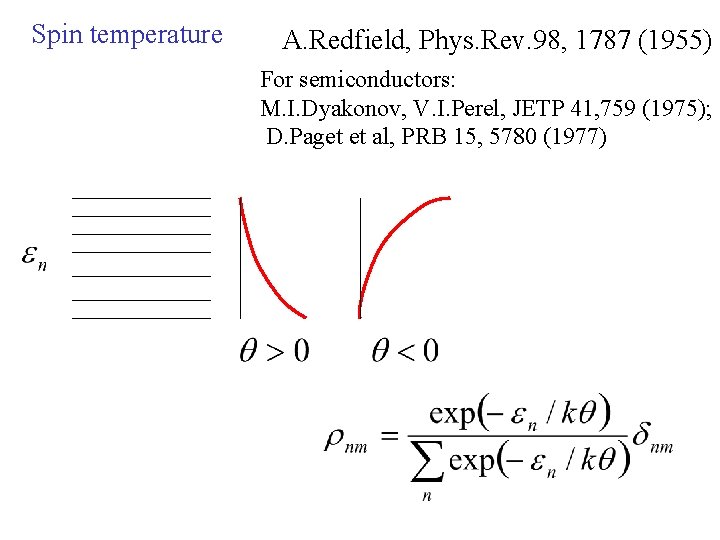
Spin temperature A. Redfield, Phys. Rev. 98, 1787 (1955) For semiconductors: M. I. Dyakonov, V. I. Perel, JETP 41, 759 (1975); D. Paget et al, PRB 15, 5780 (1977)

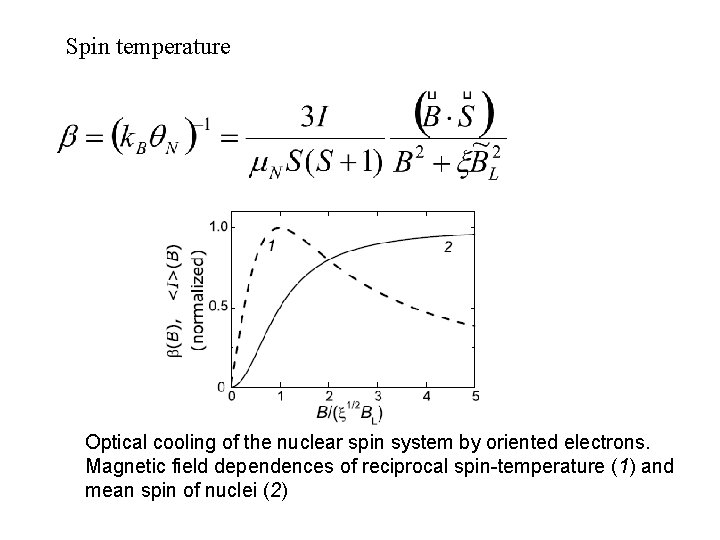
Spin temperature Optical cooling of the nuclear spin system by oriented electrons. Magnetic field dependences of reciprocal spin-temperature (1) and mean spin of nuclei (2)

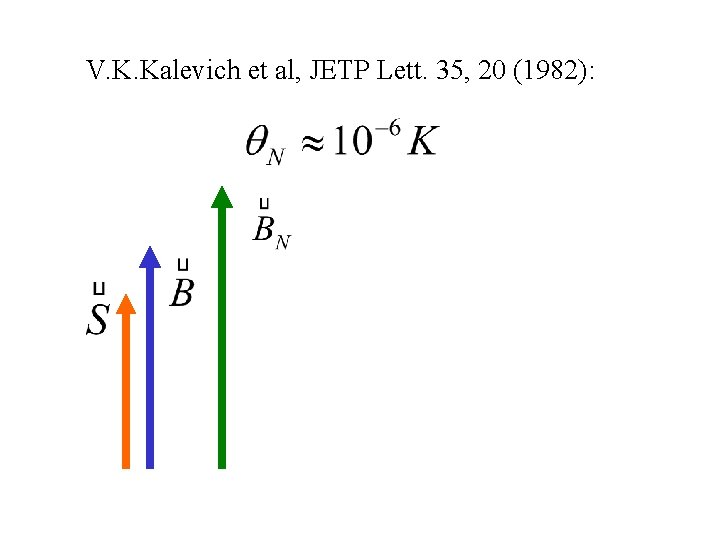
V. K. Kalevich et al, JETP Lett. 35, 20 (1982):

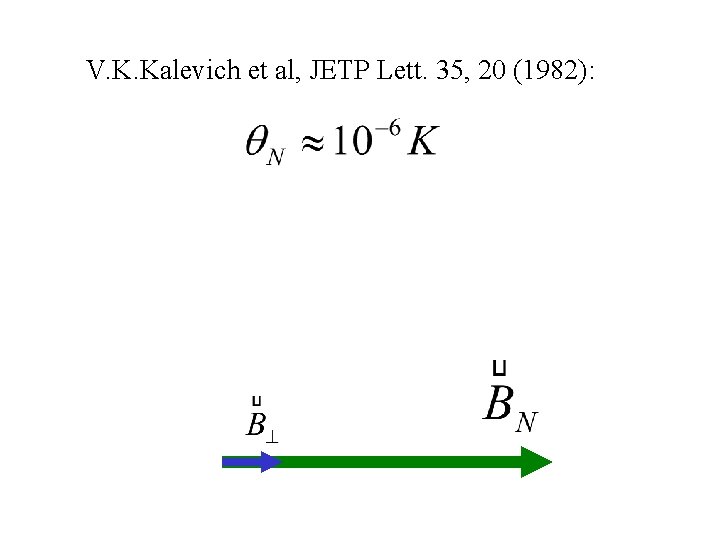
V. K. Kalevich et al, JETP Lett. 35, 20 (1982):

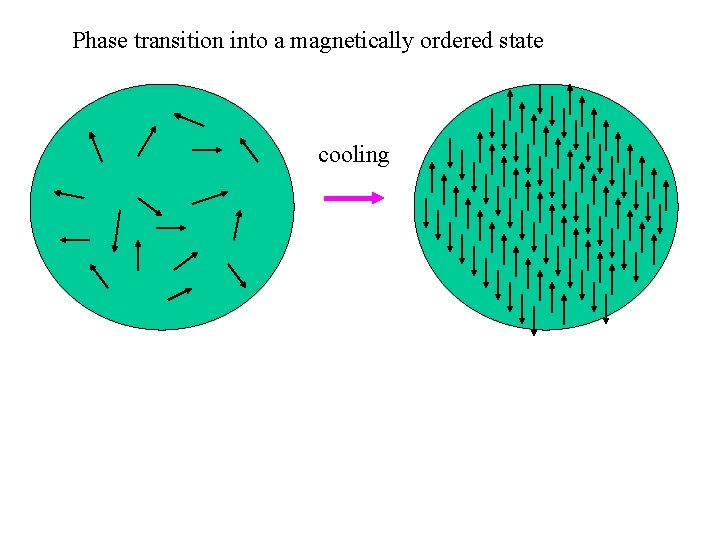
Phase transition into a magnetically ordered state cooling

Nuclear spin ordering Experiment and theory (rotating frame, Ca. F 2, Li. H): Abragam group, 1970 s Ferromagnetic or antiferromagnetic Theory for Ga. As (laboratory frame): Merkulov, Papava, Ponomarenko, Vasiliev, Can. J. Phys. 66, 135 (1988) antiferromagnetic =-10 -8 K =5. 10 -7 K P=85% P=55%

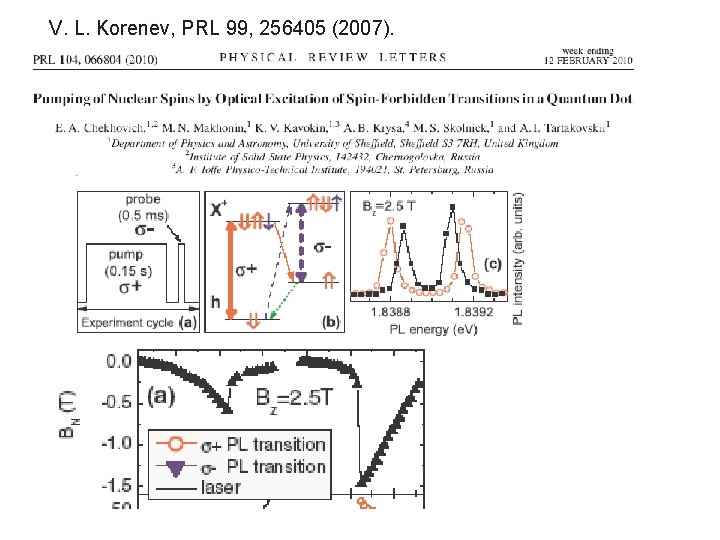
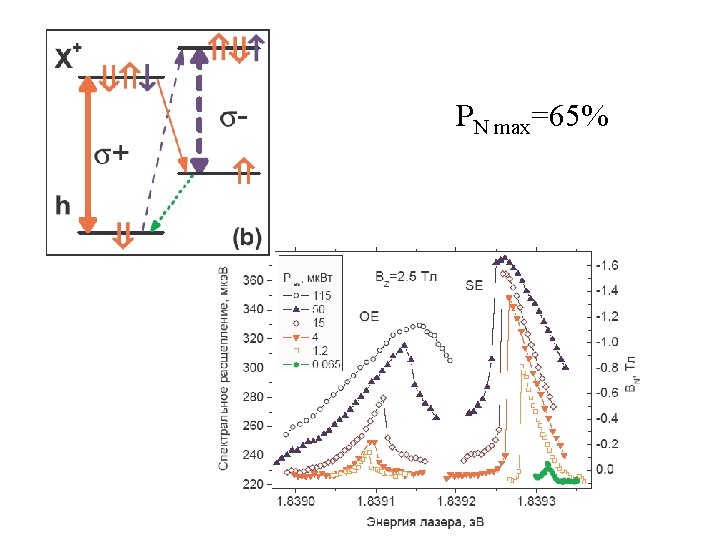
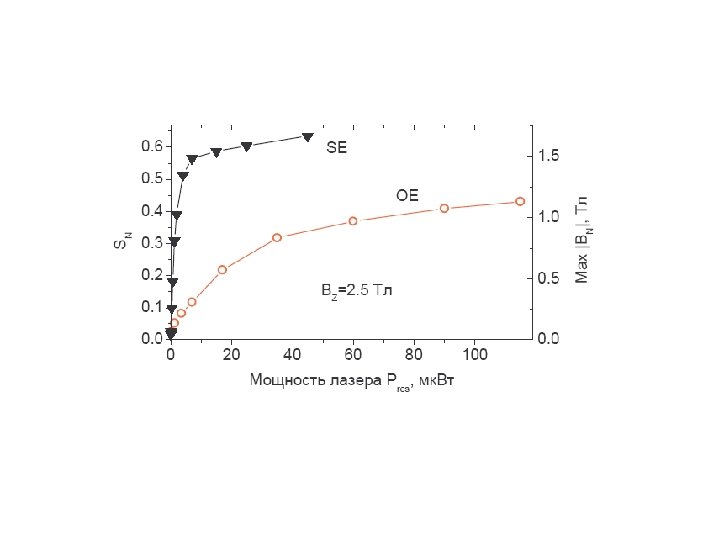
V. L. Korenev, PRL 99, 256405 (2007).

PN max=65%

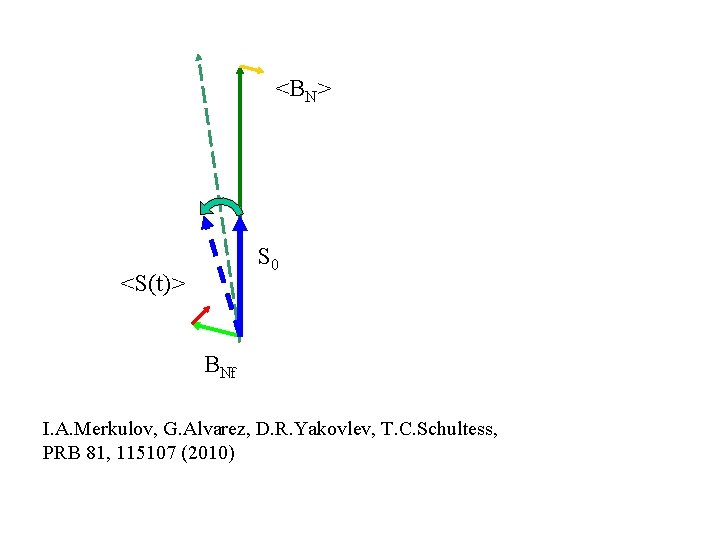
<BN> S 0 <S(t)> BNf I. A. Merkulov, G. Alvarez, D. R. Yakovlev, T. C. Schultess, PRB 81, 115107 (2010)

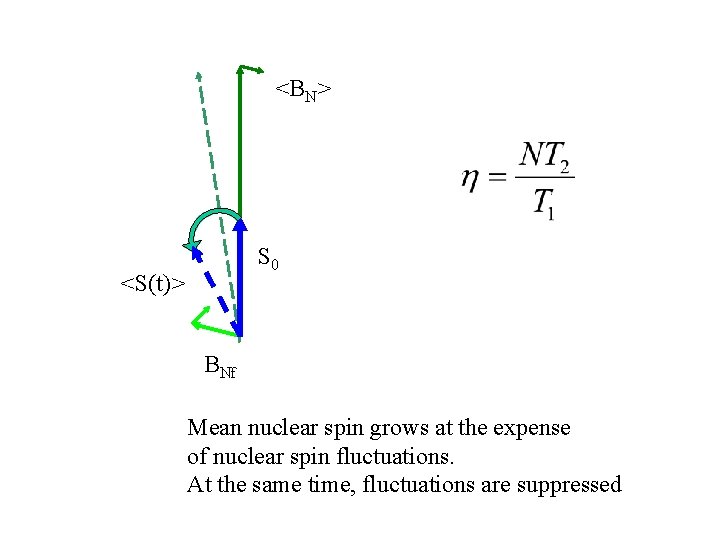
<BN> S 0 <S(t)> BNf Mean nuclear spin grows at the expense of nuclear spin fluctuations. At the same time, fluctuations are suppressed

Summary 1) Dynamical polarization of nuclei in semiconductors produces very strong, classical magnetic fields affecting electron spins. This can be directly observed in optical spectra of individual quantum dots. 2) Shifts of electron spin levels in nuclear fields result in nonlinear effects and a theoretical possibility of self-polarization. 3) The nuclear spin system can be cooled down to microkelvins. If we manage to cool it further down, we could freeze nuclear spins and obtain a nuclear antiferromagnet with strongly reduced fluctuations. 4) To do this, we have to reach high nuclear polarization, which is not so easy…