Electronic States of Atoms Quantum numbers for electrons

Electronic States of Atoms Quantum numbers for electrons Quantum numbers for many-electron atoms l: orbital angular momentum quantum number (0, 1, … n-1 where 0=s, 1=p, 2=d, 3=f) L: orbital angular momentum quantum number ml: orbital magnetic quantum number (l, l-1, …, 0, …, -l ) ML: orbital magnetic quantum number (Sml) 2 L+1 possible values s: electron spin quantum number (1/2) S: total spin quantum number S = s 1+s 2, s 1+s 2 -1, …, | s 1 -s 2 | S = 0 singlet, S = 1 doublet, S = 2 triplet ms: spin magnetic quantum number (+1/2, -1/2) MS: spin magnetic quantum number (Sms) 2 S+1 possible values e. g. , for 2 e-: L = l 1+l 2, l 1+l 2 -1, l 1+l 2 -2, …, | l 1 -l 2 | 0 = S, 1 = P, 2 = D, 3 = F J: total angular quantum number J = L+S, L+S-1, …, | L-S|

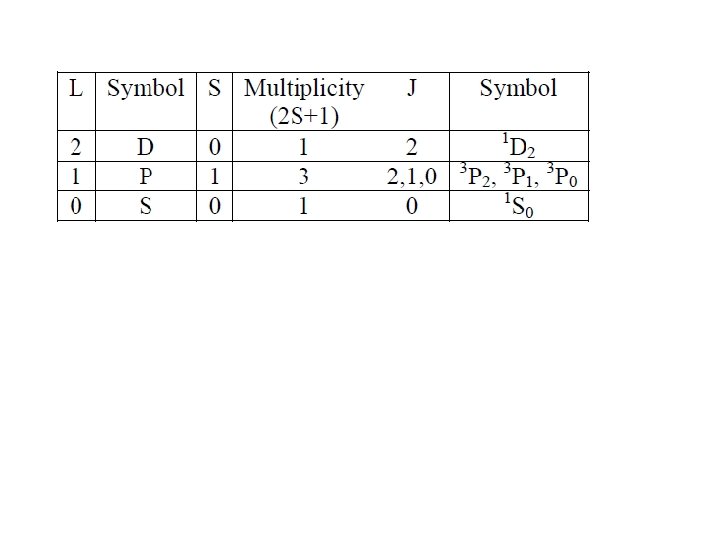
Spectroscopic Description of Atomic Electronic States – Term Symbols Multiplicity (2 S +1) describes the number of possible orientations of total spin angular momentum where S is the resultant spin quantum number (1/2 x # unpaired electrons) Resultant Angular Momentum (L) describes the coupling of the orbital angular momenta of each electron (add the m. L values for each electron) Total Angular Momentum (J) combines orbital angular momentum and intrinsic angular momentum (i. e. , spin). To Assign J Value: if less than half of the subshell is occupied, take the minimum value J =|L−S|; if more than half-filled, take the maximum value J = L + S; if the subshell is half-filled, L = 0 and then J = S.

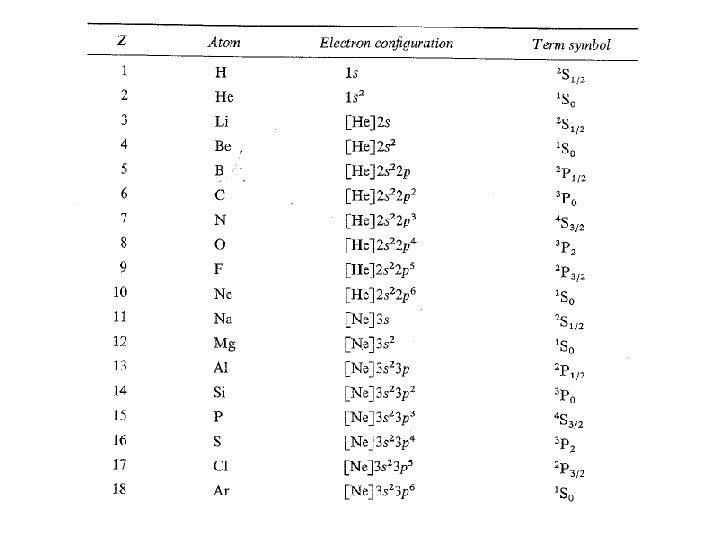
Spectroscopic Description of Ground Electronic States – Term Symbols Term Symbol Form: 2 S+1{L} J 2 S+1 – multiplicity L – resultant angular momentum quantum number J – total angular momentum quantum number Ground state has maximal S and L values. Example: Ground State of Sodium – 1 s 22 p 63 s 1 Consider only the one valence electron (3 s 1) L = l = 0, S = s = ½, J=L+S=½ so, the term symbol is 2 S½

Are you getting the concept? Write the ground state term symbol for fluorine.

Spectroscopic Description of All Possible Electronic States – Term Symbols C – 1 s 22 p 2 Step 1: Consider two valence p electrons 1 st 2 p electron has n = 2, l = 1, ml = 0, ± 1, ms = ±½ → 6 possible sets of quantum numbers 2 nd 2 p electron has 5 possible sets of quantum numbers (Pauli Exclusion Principle) For both electrons, (6 x 5)/2 = 15 possible assignments since the electrons are indistinguishable Step 2: Draw all possible microstates. Calculate ML and MS for each state.

Step 2: Draw all possible microstates. Calculate ML and MS for each state.

Spectroscopic Description of All Possible Electronic States – Term Symbols C – 1 s 22 p 2 Step 3: Count the number of microstates for each ML—MS possible combination Step 4: Extract smaller tables representing each possible term

Spectroscopic Description of All Possible Electronic States – Term Symbols C – 1 s 22 p 2 Step 5: Use Hund’s Rules to determine the relative energies of all possible states. 1. The highest multiplicity term within a configuration is of lowest energy. 2. For terms of the same multiplicity, the highest L value has the lowest energy (D < P < S). 3. For subshells that are less than half-filled, the minimum J-value state is of lower energy than higher J-value states. 4. For subshells that are more than half-filled, the state of maximum J-value is the lowest energy. Based on these rules, the ground electronic configuration for carbon has the following energy order: 3 P 0 < 3 P 1 < 3 P 2 < 1 D 2 < 1 S 0

Hund’s Rules