Electron Orbitals Cartoon courtesy of labinitio com Quantum

Electron Orbitals Cartoon courtesy of lab-initio. com

Quantum Mechanical Model of the Atom Mathematical laws can identify the regions outside of the nucleus where electrons are most likely to be found. These laws are beyond the scope of this class…

Heisenberg Uncertainty Principle “One cannot simultaneously determine both the position and momentum of an electron. ” The more certain you are about where the electron is, the less certain you can be about where it is going. Werner Heisenberg The more certain you are about where the electron is going, the less certain you can be about where it is.

Quantum Numbers Each electron in an atom has a unique set of 4 quantum numbers which describe it. v Principal quantum number v Angular momentum quantum number v Magnetic quantum number v Spin quantum number
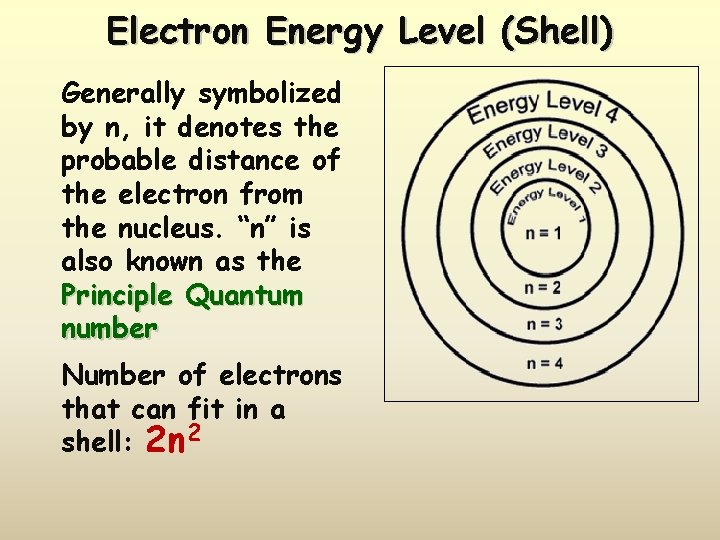
Electron Energy Level (Shell) Generally symbolized by n, it denotes the probable distance of the electron from the nucleus. “n” is also known as the Principle Quantum number Number of electrons that can fit in a shell: 2 n 2

Electron Orbitals An orbital is a region within an energy level where there is a probability of finding an electron. Orbital shapes are defined as the surface that contains 90% of the total electron probability. The angular momentum quantum number, generally symbolized by l, denotes the orbital (subshell) in which the electron is located.
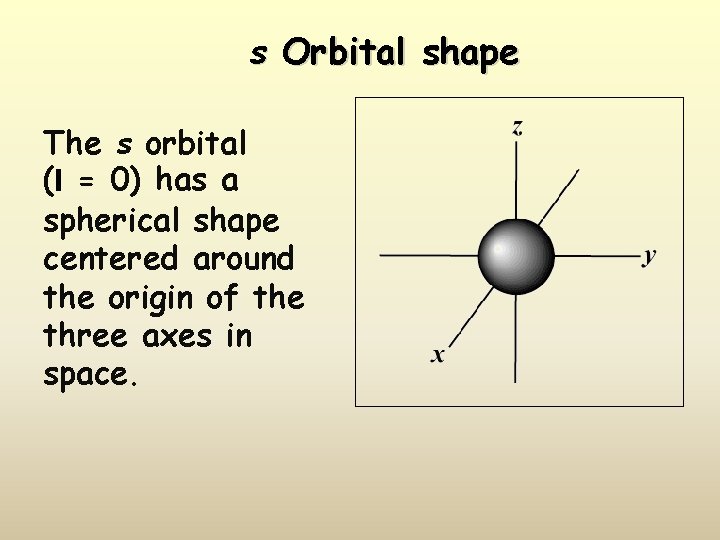
s Orbital shape The s orbital (l = 0) has a spherical shape centered around the origin of the three axes in space.
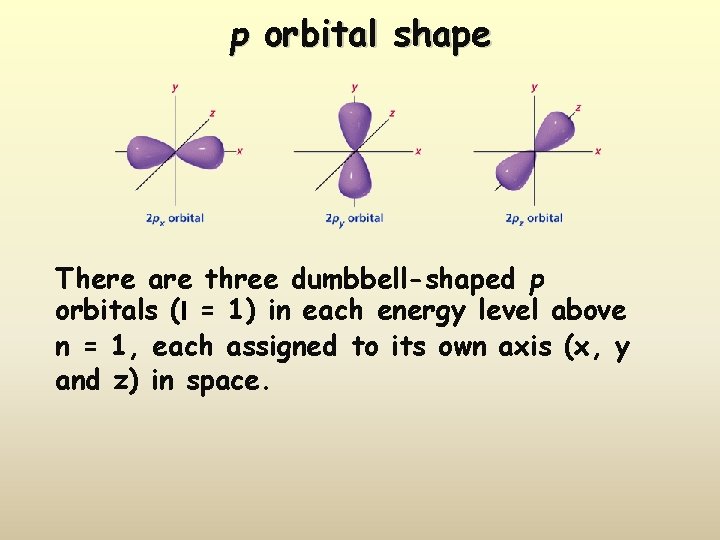
p orbital shape There are three dumbbell-shaped p orbitals (l = 1) in each energy level above n = 1, each assigned to its own axis (x, y and z) in space.

d orbital shapes Things get a bit more complicated with the five d orbitals (l = 2) that are found in the d sublevels beginning with n = 3. To remember the shapes, think of “double dumbells” …and a “dumbell with a donut”!
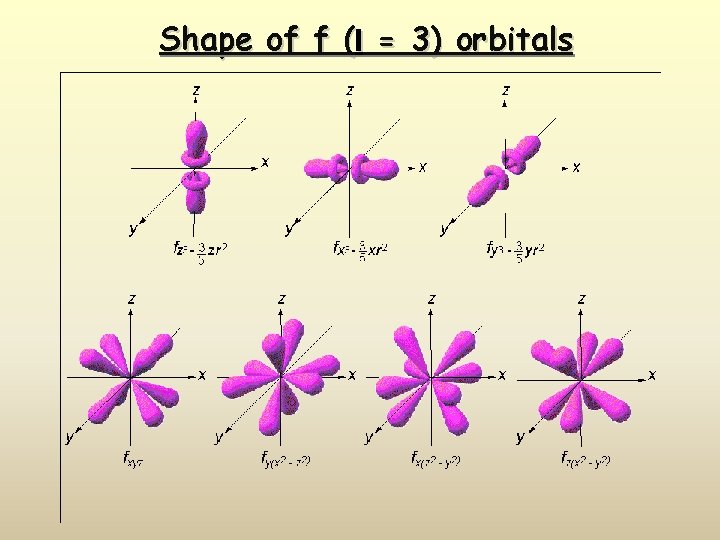
Shape of f (l = 3) orbitals

Energy Levels, Sublevels, Electrons Energy Level (n) Sublevels in main energy level (n sublevels) Number of orbitals per sublevel Number of Electrons per sublevel Number of electrons per main energy level (2 n 2) 1 s 1 2 2 2 s p 1 3 2 6 8 3 s p d 1 3 5 2 6 10 18 4 s p d f 1 3 5 7 2 6 10 14 32
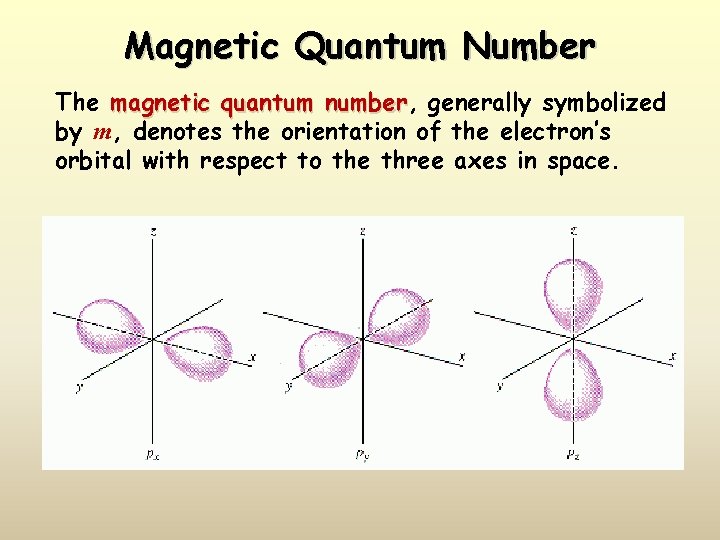
Magnetic Quantum Number The magnetic quantum number, number generally symbolized by m, denotes the orientation of the electron’s orbital with respect to the three axes in space.
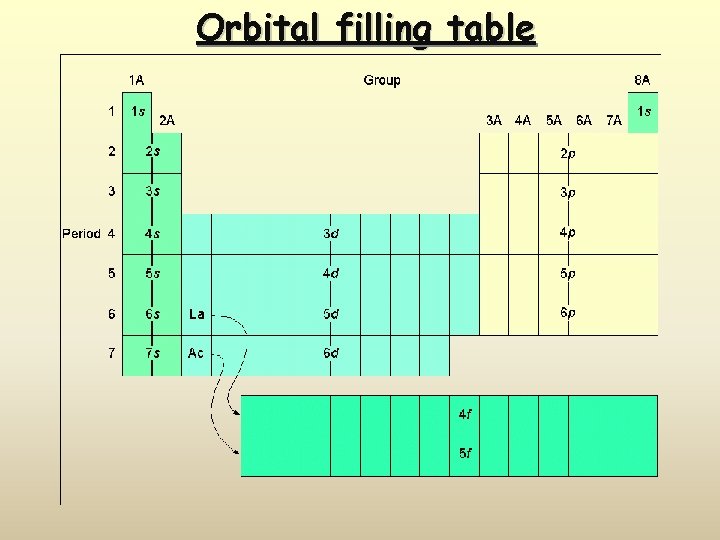
Orbital filling table

Electron Spin The Spin Quantum Number describes the behavior (direction of spin) of an electron within a magnetic field. Possibilities for electron spin:

Pauli Exclusion Principle Two electrons occupying the same orbital must have opposite spins Wolfgang Pauli
![Element Lithium Configuration notation Orbital notation 1 s 22 s 1 [He]2 s 1 Element Lithium Configuration notation Orbital notation 1 s 22 s 1 [He]2 s 1](http://slidetodoc.com/presentation_image_h/cd8706ea17cb5b399fa2d36b6be70acf/image-16.jpg)
Element Lithium Configuration notation Orbital notation 1 s 22 s 1 [He]2 s 1 ____ 1 s Beryllium ____ 2 p ____ 2 s ____ 2 p ____ [He]2 s 2 p 2 ____ 2 s ____ 2 p ____ 1 s 22 s 2 p 3 [He]2 s 2 p 3 ____ 2 s ____ 2 p ____ 1 s 22 s 2 p 4 [He]2 s 2 p 4 ____ 2 s ____ 2 p ____ 1 s 22 s 2 p 5 [He]2 s 2 p 5 ____ 1 s Neon ____ 2 s 1 s 22 s 2 p 2 ____ 1 s Fluorine ____ [He]2 s 2 p 1 ____ 1 s Oxygen ____ 2 p 1 s 22 s 2 p 1 ____ 1 s Nitrogen ____ [He]2 s 2 ____ 1 s Carbon ____ 2 s 1 s 22 s 2 ____ 1 s Boron Noble gas notation ____ 2 s ____ 2 p ____ 1 s 22 s 2 p 6 [He]2 s 2 p 6 ____ 1 s ____ 2 s ____ 2 p ____

Exclusion Warning! Assigning quantum numbers to electrons has been exluded and will not be tested! The following slides are purely for your entertainment

Assigning the Numbers v The three quantum numbers (n, l, and m) are integers. v The principal quantum number (n) cannot be zero. v n must be 1, 2, 3, etc. v The angular momentum quantum number (l ) can be any integer between 0 and n - 1. v For n = 3, l can be either 0, 1, or 2. v The magnetic quantum number (ml) can be any integer between -l and +l. v For l = 2, m can be either -2, -1, 0, +1, +2.

Quantum numbers for the first four levels of orbitals in the hydrogen atom n l Orbital designation ml # of orbitals 1 0 1 s 0 1 2 0 2 s 0 1 1 2 p -1, 0, 1 3 0 3 s 0 1 1 3 p -1, 0, 1 3 2 3 d -2, -1, 0, 1, 2 5 0 4 s 0 1 1 4 p -1, 0, 1 3 2 4 d -2, -1, 0, 1, 2 5 3 4 f -3, -2, -1, 0, 1, 2, 3 7 3 4
- Slides: 19