Electron molecule collision calculations using the Rmatrix method

Electron molecule collision calculations using the R-matrix method Jonathan Tennyson Department of Physics and Astronomy University College London IAEA. Vienna, December 2003

Processes: at low impact energies Elastic scattering AB + e Electronic excitation AB + e AB* + e Vibrational excitation AB(v”=0) + e AB(v’) + e Rotational excitation AB(N”) + e AB(N’) + e Dissociative attachment / Dissociative recombination AB + e A + B Impact dissociation AB + e A+B+e All go via (AB )**. Can also look for bound states

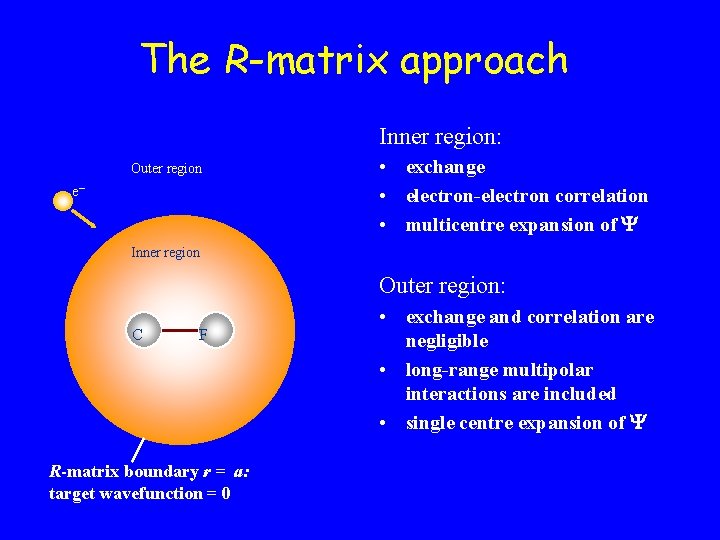
The R-matrix approach Inner region: Outer region e– • exchange • electron-electron correlation • multicentre expansion of Inner region Outer region: C C F R-matrix boundary r = a: target wavefunction = 0 • exchange and correlation are negligible • long-range multipolar interactions are included • single centre expansion of

Scattering Wavefunctions Yk = A i, j ai, j, k fi. N hi, j + bj, k fj. N+1 where N fi N-electron wavefunction of ith target state hi, j 1 -electron continuum wavefunction N+1 fj (N+1)-electron short-range functions A Antisymmetrizes the wavefunction ai, j, k and bj, k variationally determined coefficients

UK R-matrix codes L. A. Morgan, J. Tennyson and C. J. Gillan, Computer Phys. Comms. , 114, 120 (1999).

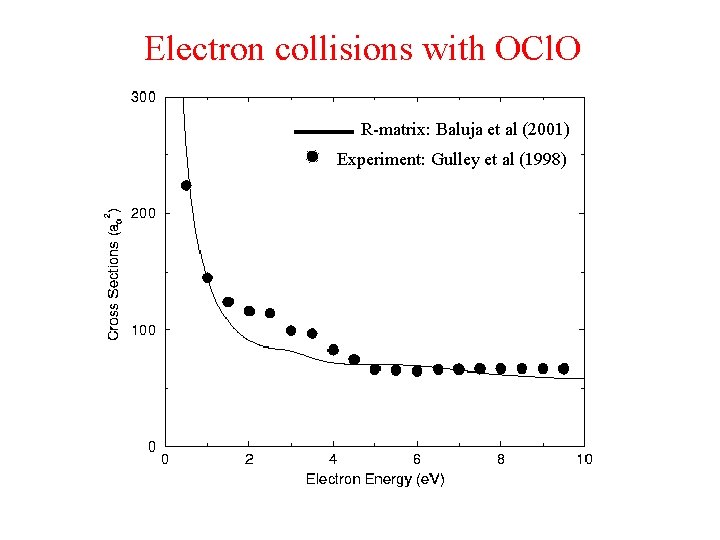
Electron collisions with OCl. O R-matrix: Baluja et al (2001) Experiment: Gulley et al (1998)

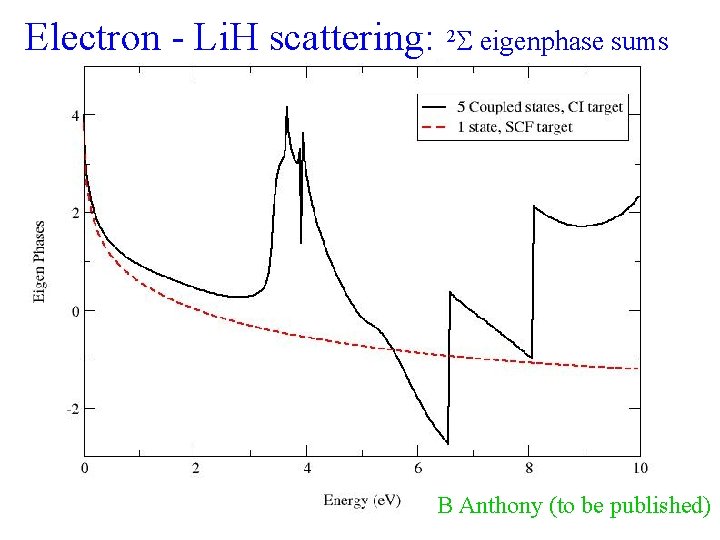
Electron - Li. H scattering: 2 eigenphase sums B Anthony (to be published)

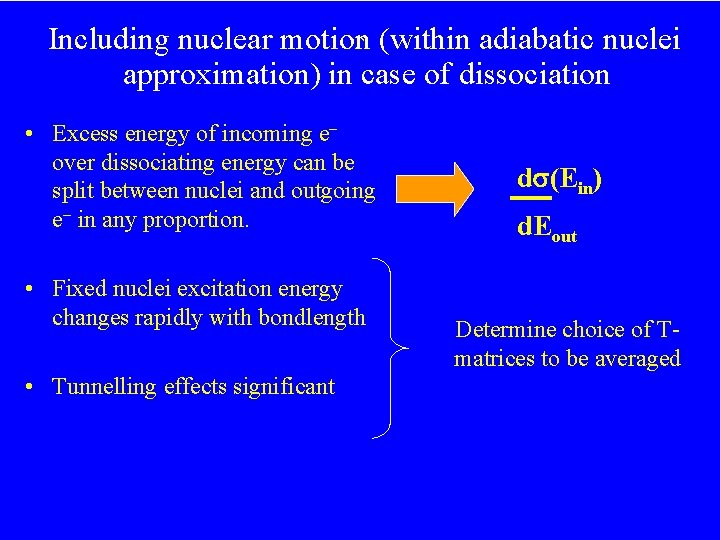
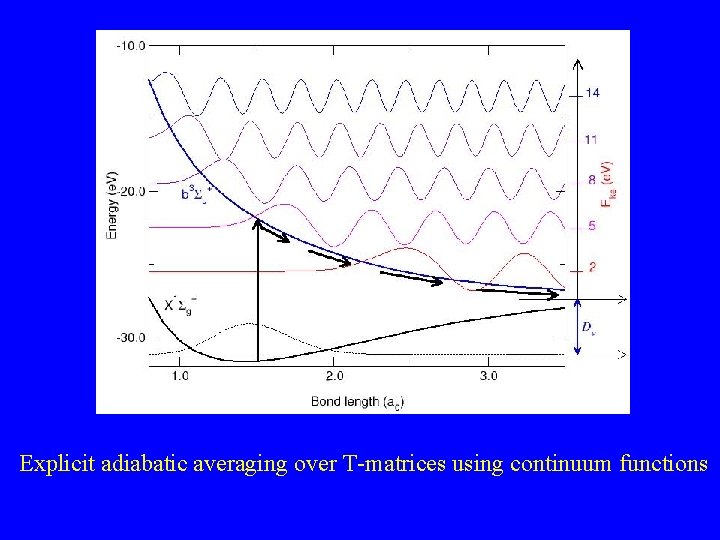
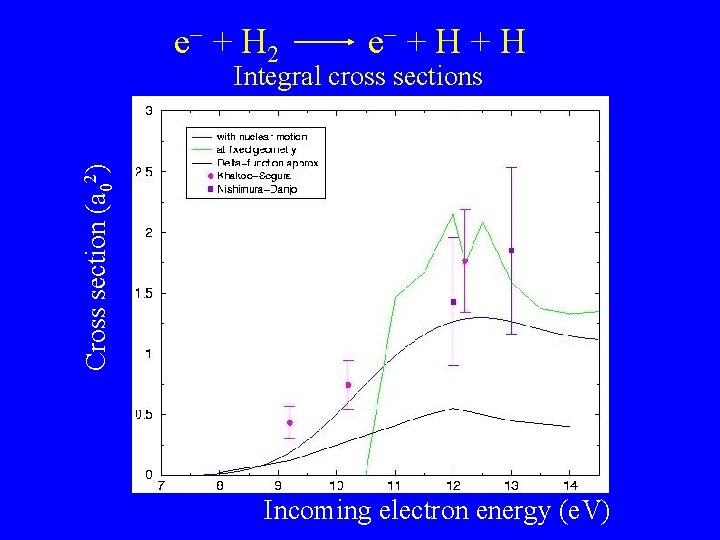
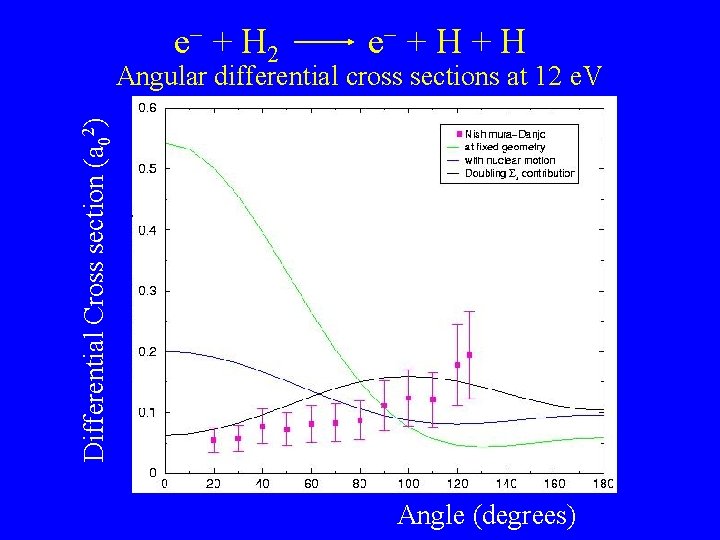
Electron impact dissociation of H 2 Important for fusion plasma and astrophysics Low energy mechanism: e + H 2(X 1 g) e + H 2(b 3 u) e + H R-matrix calculations based on adiabatic nuclei approximation extended to dissociation

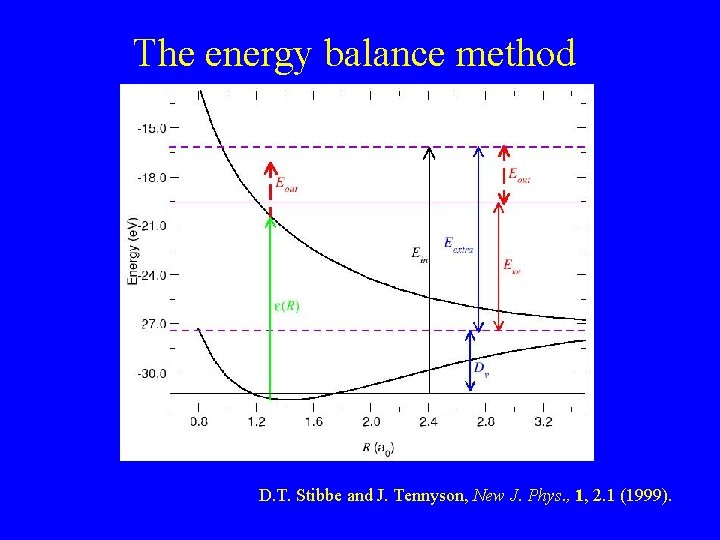
Including nuclear motion` (within adiabatic nuclei approximation) in case of dissociation • Excess energy of incoming e over dissociating energy can be split between nuclei and outgoing e in any proportion. • Fixed nuclei excitation energy changes rapidly with bondlength • Tunnelling effects significant d (Ein) d. Eout Determine choice of Tmatrices to be averaged

The energy balance method D. T. Stibbe and J. Tennyson, New J. Phys. , 1, 2. 1 (1999).

Explicit adiabatic averaging over T-matrices using continuum functions

Need to Calculate: • Total cross sections, (Ein) • Energy differential cross sections, d (Ein) d. Eout • Angular differential cross sections, d (Ein) dq • Double differential cross sections, d 2 (Ein) dqd. Eout Required formulation of the problem C. S. Trevisan and J. Tennyson, J. Phys. B: At. Mol. Opt. Phys. , 34, 2935 (2001)

e + H 2 e + H Cross section (a 02) Integral cross sections Incoming electron energy (e. V)

e + H 2 e + H Differential Cross section (a 02) Angular differential cross sections at 12 e. V Angle (degrees)

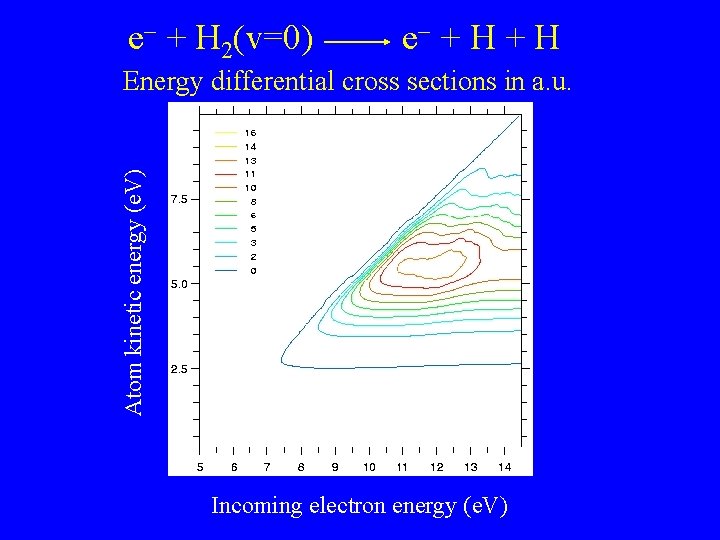
e + H 2(v=0) e + H Atom kinetic energy (e. V) Energy differential cross sections in a. u. Incoming electron energy (e. V)

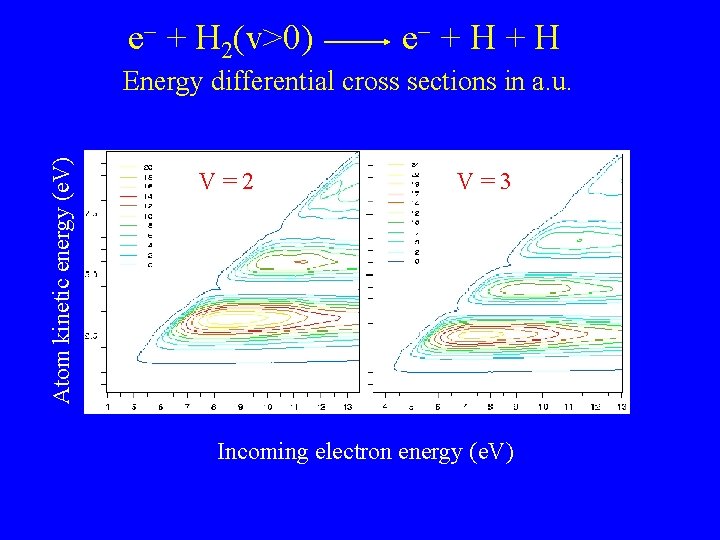
e + H 2(v>0) e + H Atom kinetic energy (e. V) Energy differential cross sections in a. u. V=2 V=3 Incoming electron energy (e. V)

Electron impact dissociation of H 2 Effective threshold about 8 e. V for H 2(v=0) Thermal rates strongly dependent on initial H 2 vibrational state For v=0: Excess energy largely converted to Kinetic Energy of outgoing H atoms For v > 0: Source of cold H atoms ?

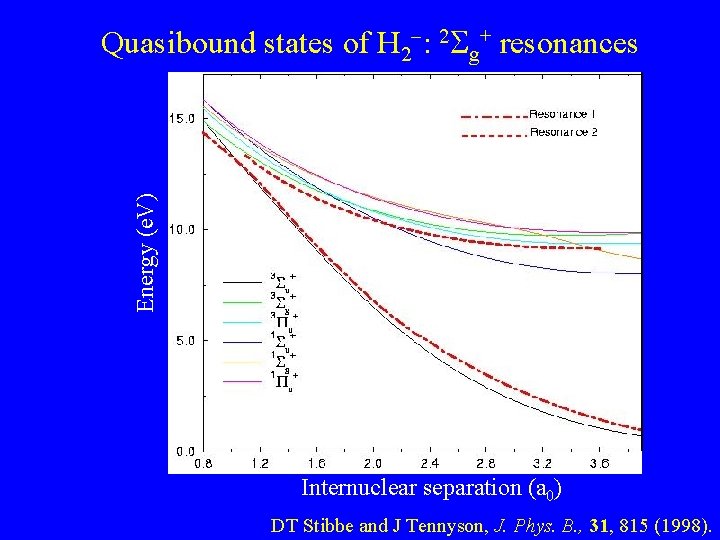
Energy (e. V) Quasibound states of H 2 : 2 g+ resonances Internuclear separation (a 0) DT Stibbe and J Tennyson, J. Phys. B. , 31, 815 (1998).

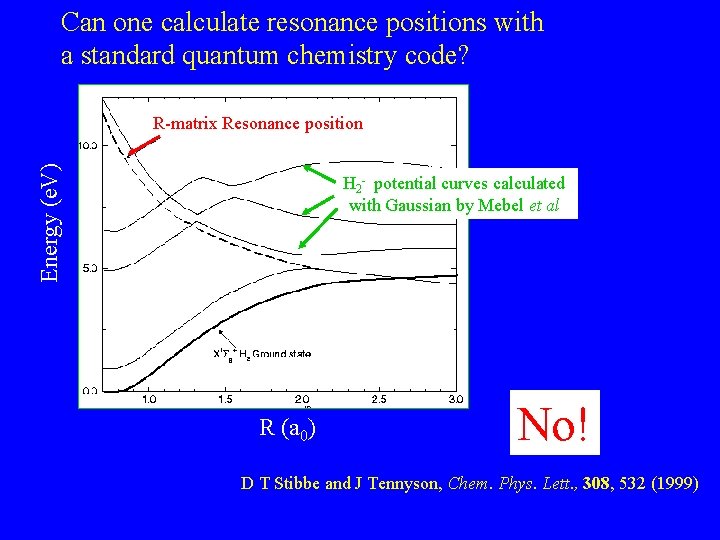
Can one calculate resonance positions with a standard quantum chemistry code? Energy (e. V) R-matrix Resonance position H 2 - potential curves calculated with Gaussian by Mebel et al. R (a 0) No! D T Stibbe and J Tennyson, Chem. Phys. Lett. , 308, 532 (1999)

Electron collision with CFx radicals extremely high global warming potential C 2 F 6 and CF 4 practically infinite atmospheric lifetimes CF 3 I C 2 F 4 new feedstock gases low global warming potential strong source of CFx radicals no information on how they interact with low E e– CFx radicals highly reactive, difficult species to work with in labs Theoretical approaches – attractive source of information

Twin-track approach Joint experimental and theoretical project e– interactions with the CF 3 I and C 2 F 4 e– collisions with the CF, CF 2 and CF 3 N. J. Mason, P. Limao-Vieira and S. Eden I. Rozum and J. Tennyson

Electron collisions with the CF Target model • X 1 , 4 –, 2 +, 2 – and 4 • Slater type basis set: (24 , 14 ) + ( , ) C valence target states valence NO single + double excitation (24 , 14 ) final model 2 + Rydberg state Rydberg NO ( ) single excitation (7 … 14 3 … 6 ) (1 2 )4(3 … 6 1 2 )11 (1 2 )4(3 … 6 1 2 )10(7 3 )1 F

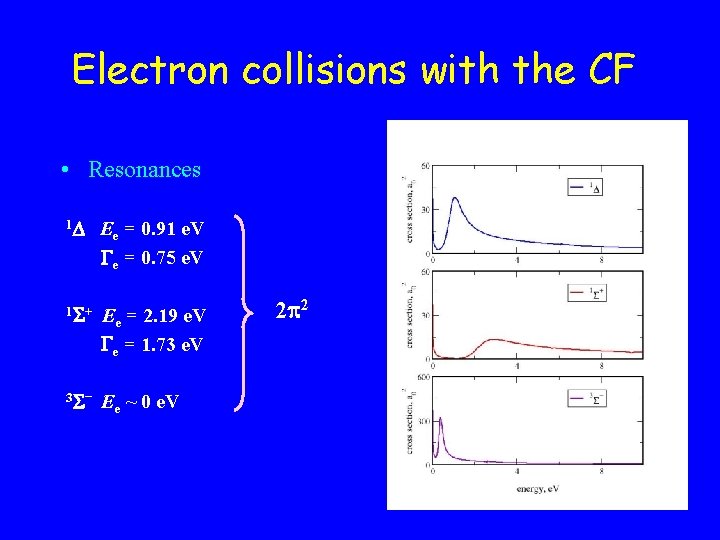
Electron collisions with the CF • Resonances 1 Ee = 0. 91 e. V e = 0. 75 e. V 1 + Ee = 2. 19 e. V e = 1. 73 e. V 3 – Ee ~ 0 e. V 2 2

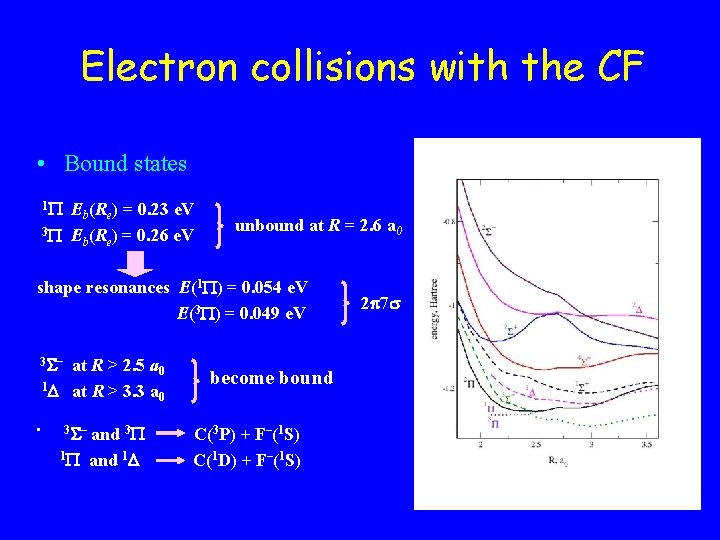
Electron collisions with the CF • Bound states 1 Eb(Re) = 0. 23 e. V 3 E (R ) = 0. 26 e. V b e unbound at R = 2. 6 a 0 shape resonances E(1 ) = 0. 054 e. V E(3 ) = 0. 049 e. V 3 – at R > 2. 5 a 0 1 at R > 3. 3 a 0 • 3 – and 3 1 and 1 become bound C(3 P) + F–(1 S) C(1 D) + F–(1 S) 2 7

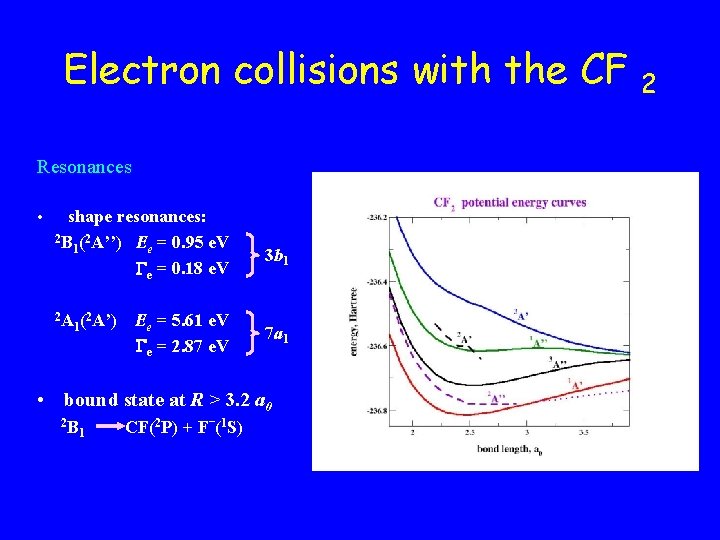
Electron collisions with the CF Resonances • shape resonances: 2 B (2 A’’) E = 0. 95 e. V 1 e e = 0. 18 e. V 2 A 1( 2 A’) Ee = 5. 61 e. V e = 2. 87 e. V 3 b 1 7 a 1 • bound state at R > 3. 2 a 0 2 B 1 CF(2 P) + F–(1 S) 2

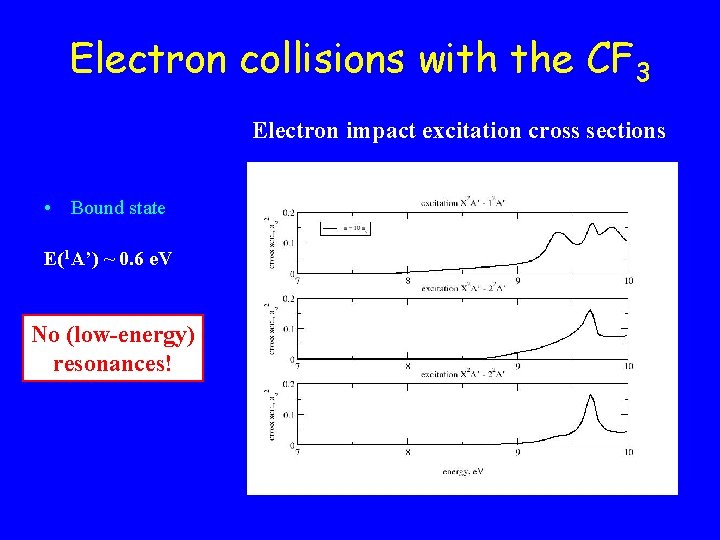
Electron collisions with the CF 3 Target representation C 2. 53 ao • Cs symmetry group • X 2 A’, 12 A”, 22 A’, 22 A”, 32 A’, 32 A” F 1 F 3 110. 7 o F 2 a = 10 ao • Models 1. (1 a’ 2 a’ 3 a’ 1 a”)8 (4 a’… 13 a’ 2 a”… 7 a”)25 240 000 CSF (Ra) 2. (1 a’… 6 a’ 1 a” 2 a”)16 (7 a’… 13 a’ 3 a”… 7 a”)17 28 000 CSF 3. (1 a’… 5 a’ 1 a” 2 a”)14 (6 a’… 13 a’ 3 a”… 7 a”)19 50 000 CSF

Electron collisions with the CF 3 Electron impact excitation cross sections • Bound state E(1 A’) ~ 0. 6 e. V No (low-energy) resonances!

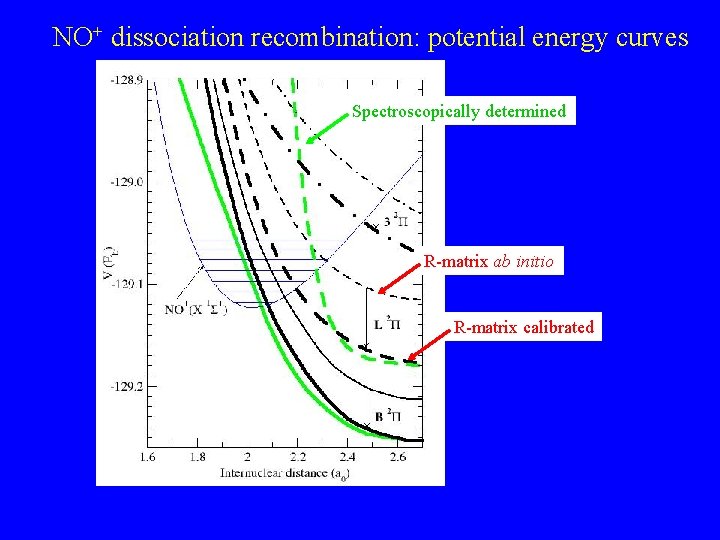
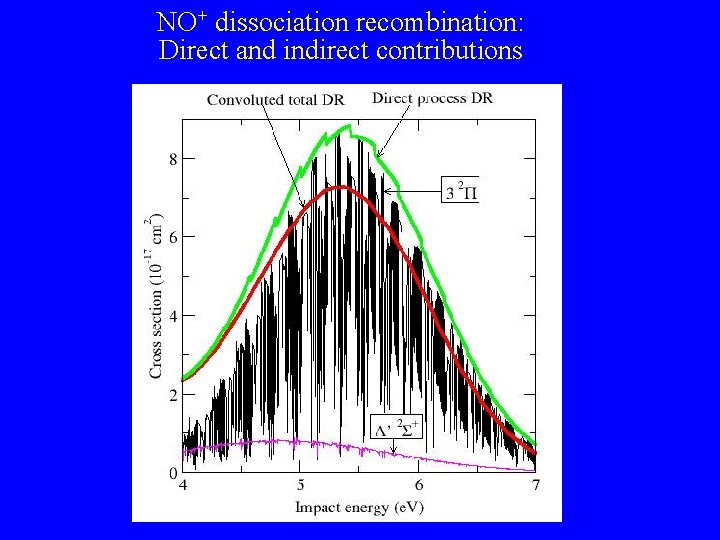
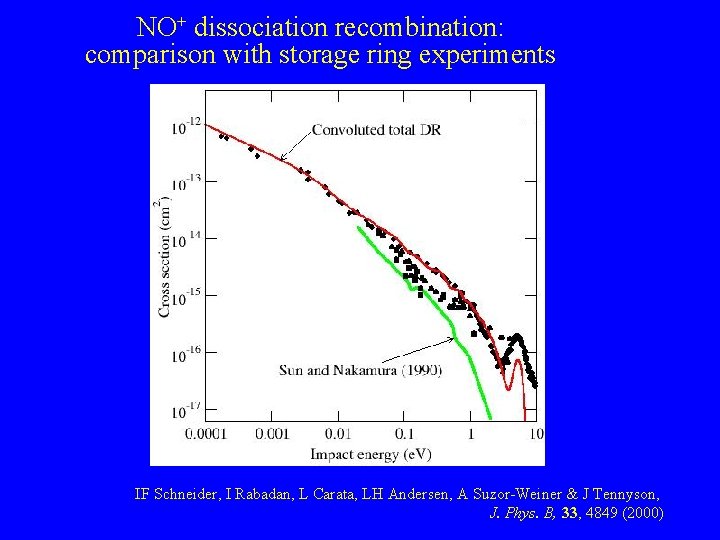
Dissociative recombination of NO+ important ion in ionosphere of Earth and thermosphere of Venus Mainly destroyed by NO+ + e N +O Need T-dependent rates for models Recent storage ring experiments show unexplained peak at 5 e. V Calculations: • resonance curves from R-matrix calculation • nuclear motion with multichannel quantum defect theory

NO+ dissociation recombination: potential energy curves Spectroscopically determined R-matrix ab initio R-matrix calibrated

NO+ dissociation recombination: Direct and indirect contributions

NO+ dissociation recombination: comparison with storage ring experiments IF Schneider, I Rabadan, L Carata, LH Andersen, A Suzor-Weiner & J Tennyson, J. Phys. B, 33, 4849 (2000)

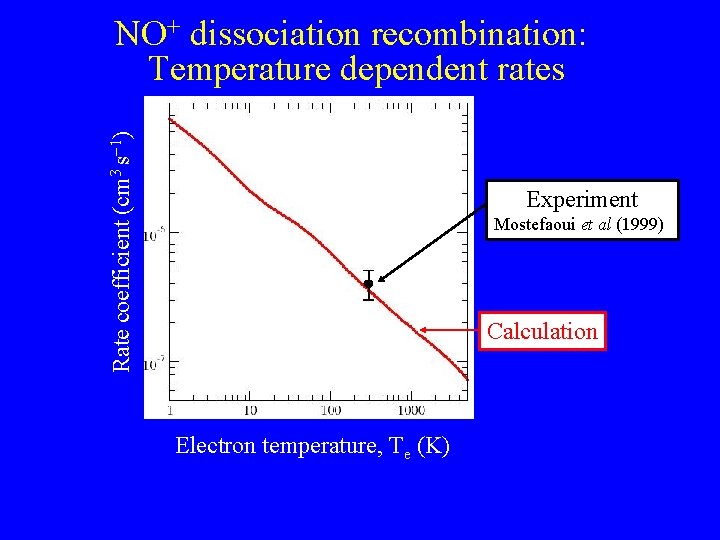
Rate coefficient (cm 3 s 1) NO+ dissociation recombination: Temperature dependent rates Experiment Mostefaoui et al (1999)) Calculation Electron temperature, Te (K)

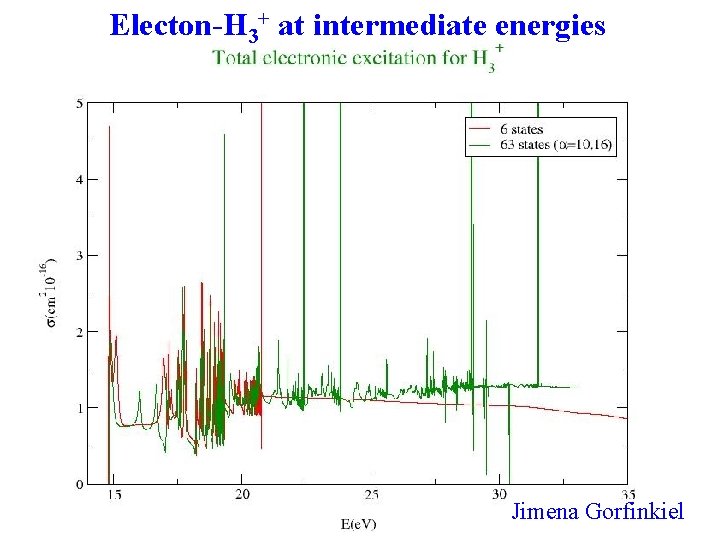
Electon-H 3+ at intermediate energies Jimena Gorfinkiel

Conclusion • R-matrix method provides a general method for treating low-energy electron collisions with neutrals, ions and radicals • Results should be reliable for the energies above 100 me. V (previous studies of Baluja et al 2001 on OCl. O). • Total elastic and electron impact excitation cross sections. • Being extended to intermediate energy and ionisation.

Chiara Piccarreta Natalia Vinci Jimena Gorfinkiel Iryna Rozum