Electron Diffusion in Liquid Argon Kirk T Mc

Electron Diffusion in Liquid Argon Kirk T. Mc. Donald Princeton University (Jan. 16, 2009) K. T. Mc. Donald Boo. Ne Collaboration Meeting Jan. 23, 2009 1 Boo. NE

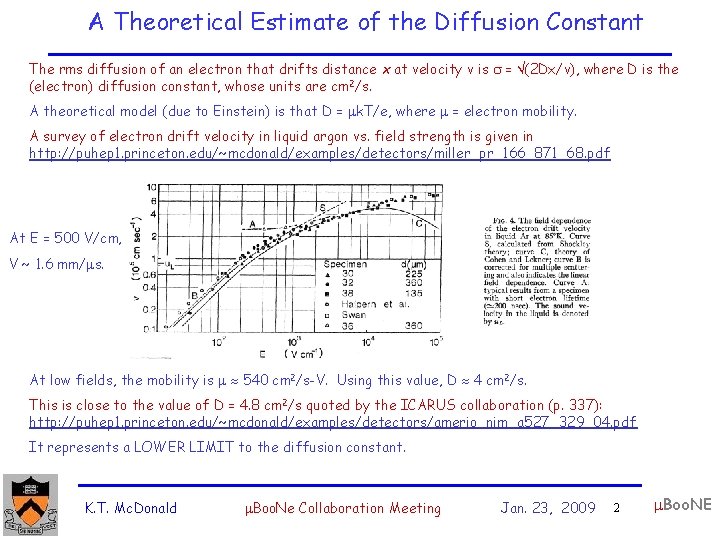
A Theoretical Estimate of the Diffusion Constant The rms diffusion of an electron that drifts distance x at velocity v is = (2 Dx/v), where D is the (electron) diffusion constant, whose units are cm 2/s. A theoretical model (due to Einstein) is that D = k. T/e, where = electron mobility. A survey of electron drift velocity in liquid argon vs. field strength is given in http: //puhep 1. princeton. edu/~mcdonald/examples/detectors/miller_pr_166_871_68. pdf At E = 500 V/cm, V ~ 1. 6 mm/ s. At low fields, the mobility is 540 cm 2/s-V. Using this value, D 4 cm 2/s. This is close to the value of D = 4. 8 cm 2/s quoted by the ICARUS collaboration (p. 337): http: //puhep 1. princeton. edu/~mcdonald/examples/detectors/amerio_nim_a 527_329_04. pdf It represents a LOWER LIMIT to the diffusion constant. K. T. Mc. Donald Boo. Ne Collaboration Meeting Jan. 23, 2009 2 Boo. NE

The Measurement of Derenzo et al. http: //puhep 1. princeton. edu/~mcdonald/examples/detectors/derenzo_nim_122_319_74. pdf report effects of diffusion in a tiny chamber (2 mm drift, 2. 7 k. V/cm) in a 1. 7 Ge. V/c - beam. The beam was along the drift direction, so the observed transverse width of the signal is the sum of the effects of diffusion along the 2 -mm track. Because the positive ions of the track remain essentially fixed during the (short) electron drift time, the attraction between the positive ions and the drifting electrons reduces the effect of diffusion. By measuring the transverse width as a function of a pulse-height cut, they infer that the effect of diffusion was = C √x where C = 28 m/(mm)1/2. Interpreting this as = √(2 D x/v) with v ~ 3. 3 mm/ s at E = 2. 7 k. V/cm, we find D ~ 13 cm 2/s. [Derenzo et al. quote D ~ 15 cm^2/s in their footnote 13, using C = 30 rather than 28. ] K. T. Mc. Donald Boo. Ne Collaboration Meeting Jan. 23, 2009 3 Boo. NE

The Measurement of Shibamura et al. http: //puhep 1. princeton. edu/~mcdonald/examples/detectors/shibamura_pra_20_2547_79. pdf report effects of diffusion in a 5 -cm-thick chamber at fields from 3. 7 to 7. 4 k. V/cm, using a 210 Po source (5. 4 Me. V). They did not directly report the diffusion constant D, but this was reported in a later paper by one of the authors, Doke, http: //puhep 1. princeton. edu/~mcdonald/examples/detectors/doke_nim_196_87_82. pdf The result is usually quoted as D = 15. 5 cm 2/s (which is the value used in the Boo. NE proposal). Because the particles is heavily ionizing ( 2 105 e-ion pairs over 50 m), once the electrons drift free from the positive ions, there may have been space-charge repulsion among the electrons that would mimic diffusion. , so that D 15. 5 cm 2/s. In the measurement of Derenzo et al, the effect of the positive ions along the track of drifting electrons would be to reduce, rather than increase the (transverse) diffusion, so we consider that they measured D 13 cm 2/s. Doke concludes (and I agree) that these two results give reasonable confidence the D 13 -15 cm 2/s in liquid argon (at electric fields around 3 k. V/cm). Shibamura et al. refer to an atomic physics model by Lekner http: //puhep 1. princeton. edu/~mcdonald/examples/detectors/lekner_pr_158_130_67. pdf that explains why D is 3 -4 times the Einstein value in liquid argon. K. T. Mc. Donald Boo. Ne Collaboration Meeting Jan. 23, 2009 4 Boo. NE

Conclusions The limited experimental data on electron diffusion in liquid argon is consistent with a value of D = 15 cm 2/s, as used in the Boo. NE proposal. This is 3 -4 times theoretical (Einstein) value quoted by the ICARUS Collaboration. The diffusion over the 2. 5 -m drift path in Boo. NE is then expected to be = (2 Dx/v) 2. 2 mm. , and the average diffusion is 2/3 this, 1. 4 mm. The average effect of diffusion is equivalent to a “shaping” time of 0. 9 s (which is added in quadrature with the “shaping” in the front-end electronics and that due to the wire spacing). The proposed use of wire (and wire-plane) spacing of 3 mm will lead to two-track resolution poorer than that limited by diffusion. That is, the effect of the wire spacing adds an effective “shaping” time (in quadrature) of about 1. 5 s (Rayleigh criterion applied to plots of B. Yu, Doc. DB 257. ) [Reducing the wire (and wire-plane) spacing to 2 mm would reduce this effective “shaping” to 1 s, and the overall “shaping” time to about 1. 7 s. ] To minimize effects of high-frequency noise, the electronic “shaping” time should be as large as does not reduce the detector resolution. Given the other two contributions to the overall “shaping” time, the electronic shaping time should be 1 s. Then the overall “shaping” of the signals will be about 2. 0 s. In this case the ADC sampling frequency interval need not be less than 1. 0 s. “Conservative” use of 1. 5 -2 MHz sampling would still provide more information than required given the intrinsic “shaping” of signals by diffusion and wire spacing. K. T. Mc. Donald Boo. Ne Collaboration Meeting Jan. 23, 2009 5 Boo. NE