Electron cloud effect for Linear Collider damping rings

Electron cloud effect for Linear Collider damping rings K. Ohmi, KEK ECLOUD 04, 19 -23 April, 2004, Napa

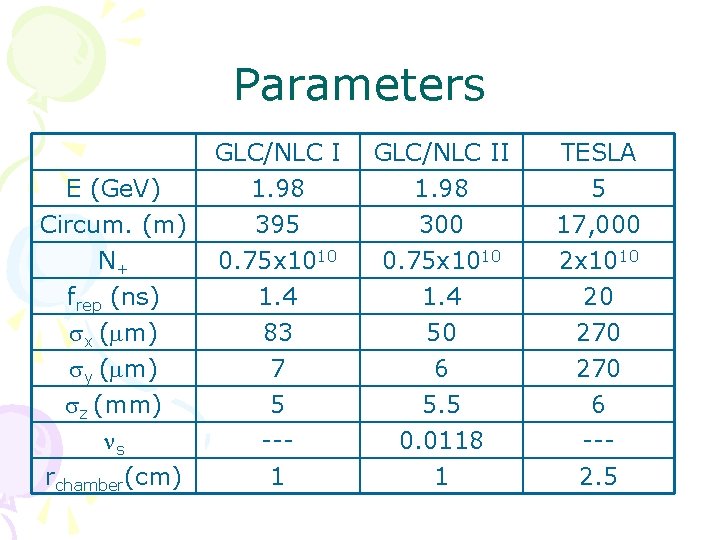
Parameters E (Ge. V) Circum. (m) N+ frep (ns) sx (mm) sy (mm) sz (mm) ns rchamber(cm) GLC/NLC I 1. 98 395 0. 75 x 1010 GLC/NLC II 1. 98 300 0. 75 x 1010 TESLA 5 17, 000 2 x 1010 1. 4 83 7 5 --1 1. 4 50 6 5. 5 0. 0118 1 20 270 6 --2. 5

Electron cloud build-up (EC 2002) • Ante-chamber R=1 cm, half width of slot 0. 5 cm. • In KEKB test ante-chamber, electron current 1/5 of cylindrical chamber was observed. • Average Photoelectron yield Y 1 g=0. 015 e-/(m. e+) for Yg=0. 65 g/(m. e+). (KEKB 0. 015 e-/(m. e+) for Yg=0. 15 g/(m. e+)) • Peak secondary yield is assumed d 2=1. 0 e/e

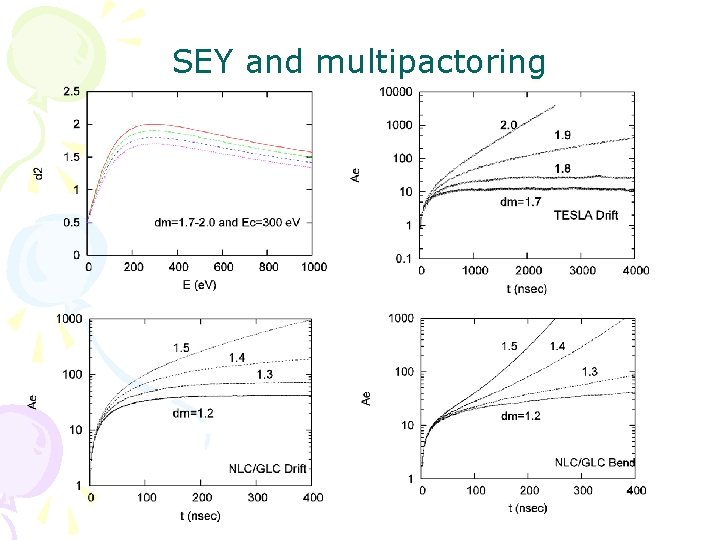
Multipacting from seed electrons • Recently, M. Pivi et al. have studied multipacting condition from starting seed electrons. • We first try to reproduce the results.

SEY and multipactoring

Requirement for SEY • GLC bend, dmax <1. 2 -1. 3. • GLC drift, dmax <1. 4 -1. 5 • TESLA drift, dmax <1. 9 Consistent with Pivi’s results dmax should be suppress to be around 1. 2.

Synchrotron radiation • Yg=0. 65(I) or 0. 86(II) g/(m. e+), (KEKB : Yg=0. 15 g/(m. e+)) • Most of photons must be protected in slot of the antechamber. • Angular divergence of synchrotron radiation K. J. Kim, S. Kamada • uc=1. 75 ke. V at E=1. 98 Ge. V, B=0. 67 T • sy=1 mrad for u=10 e. V.

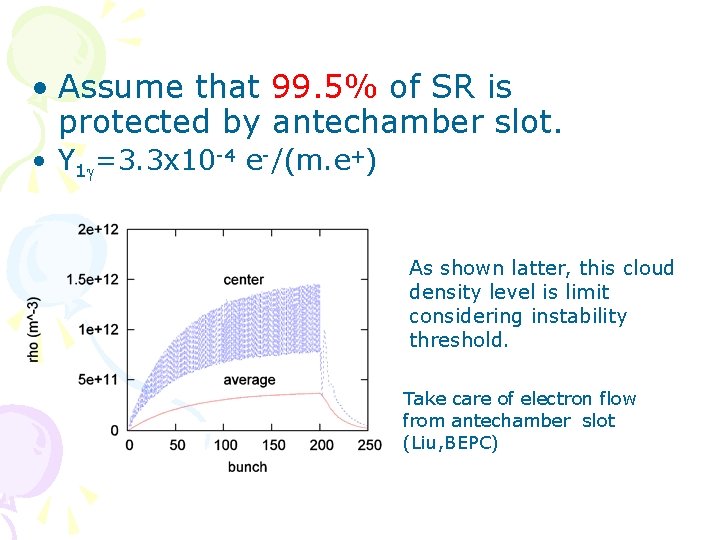
Electron density (EC 2002) 20% of SR contributes. dmax <1. Summary at 2002 • We need further reduction of the electron cloud of 1/5~1/10. The electron yield per positron and meter is required Y 1+2<0. 002 e-/(m. e+) for suppress both of the coupled and single bunch instability. Synchrotron radiation should be protected much more.

• Assume that 99. 5% of SR is protected by antechamber slot. • Y 1 g=3. 3 x 10 -4 e-/(m. e+) As shown latter, this cloud density level is limit considering instability threshold. Take care of electron flow from antechamber slot (Liu, BEPC)

Instability caused by electron cloud • Coupled bunch instability • Single bunch instability

Coupled Bunch Instability caused by electron cloud • Wake force is calculated by a numerical method as follows, l Equilibrium electron cloud. l A (i-th) bunch Dyi with a displacement passes through the cloud. l Calculate kick Dpy, j of j-th bunch. Growth of the coupled bunch instability is estimated by

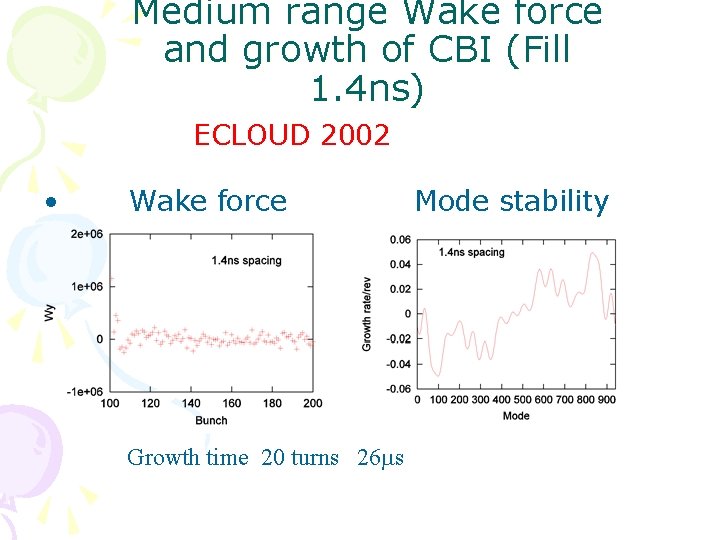
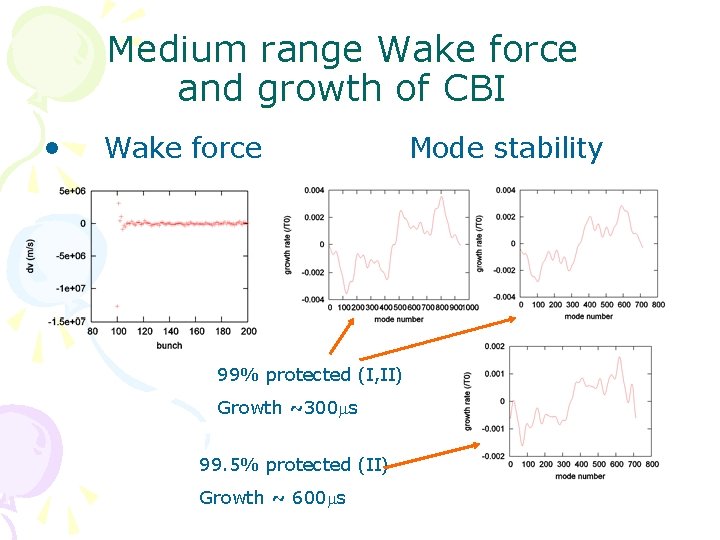
Medium range Wake force and growth of CBI (Fill 1. 4 ns) ECLOUD 2002 • Wake force Growth time 20 turns 26 ms Mode stability

Medium range Wake force and growth of CBI • Wake force 99% protected (I, II) Growth ~300 ms 99. 5% protected (II) Growth ~ 600 ms Mode stability

Single bunch instability caused by electron cloud • The single bunch instability is analyzed by wake field method and tracking simulation. Wake field • Linearized model. • Numerical calculation including nonlinearity. (Similar way to the calculation of the multi-bunch wake field)

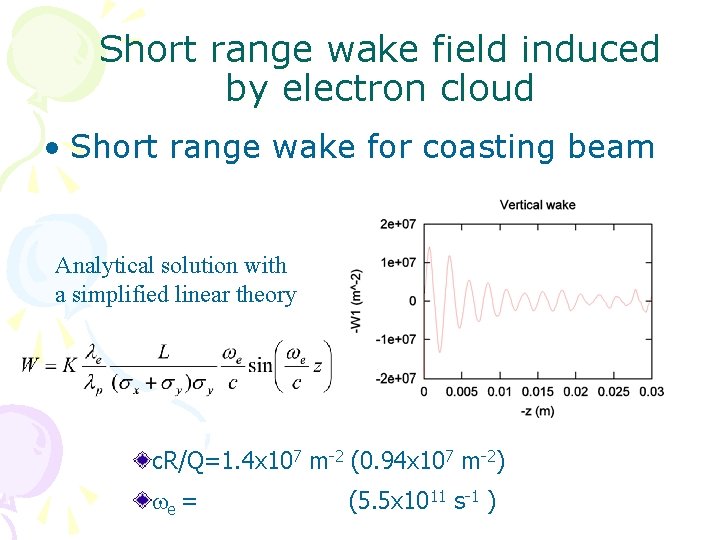
Short range wake field induced by electron cloud • Short range wake for coasting beam Analytical solution with a simplified linear theory c. R/Q=1. 4 x 107 m-2 (0. 94 x 107 m-2) we = (5. 5 x 1011 s-1 )

Threshold of fast head-tail instability • Bounce frequency of electrons in the positron beam potential wesz/c=9. 5 (V)>>1 • Coasting beam model • Stability criteria 2. 6 (H)>1

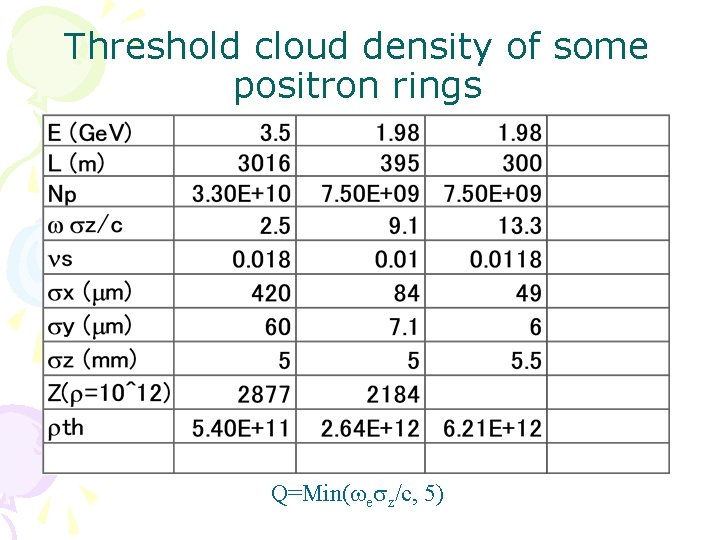
Threshold cloud density of some positron rings Q=Min(wesz/c, 5)

PIC simulation (PEHTS) • Transverse mesh. 2 D electric field calculation for electrons and positron bunch. Based on a beam simulation code for the strong-strong model (BBSSP). • A bunch was sliced into 30~50 in the longitudinal direction. • A bunch interacts with electron cloud with a projected density rex. L for each traveling of L. We choose L=C : circumference in this presentation, and the case of more interaction points in a ring L=C/n is equivalent to lower cloud density re/n.

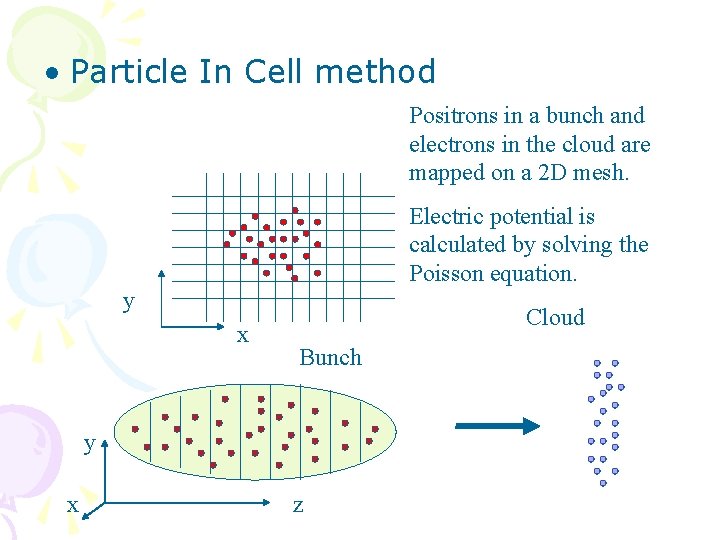
• Particle In Cell method Positrons in a bunch and electrons in the cloud are mapped on a 2 D mesh. Electric potential is calculated by solving the Poisson equation. y x Cloud Bunch y x z

Characteristics of the headtail instability • Dipole coherent motion along z. • The instability is characterized by the wake strength per a synchrotron phase advance. • The instability does not depend on the transverse tune except for a special value, for example synchro-beta resonance. • Beam size and coherent amplitude are comparable before experience of strong Landau damping. • We can distinguish whether the instability obtained by the simulation is head-tail type by investigating the above characteristics.

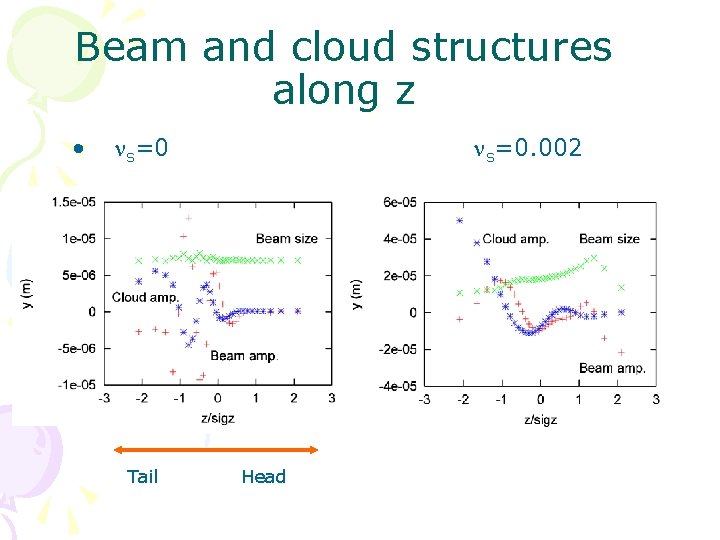
Beam and cloud structures along z • ns=0 Tail ns=0. 002 Head

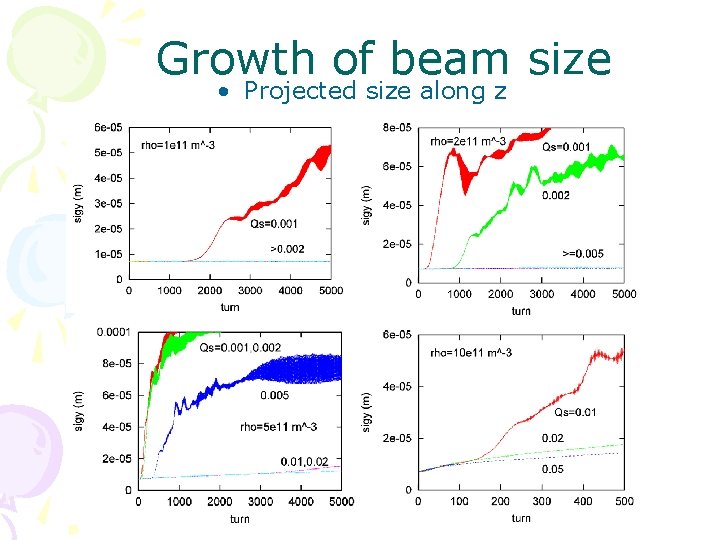
Growth of beam size • Projected size along z

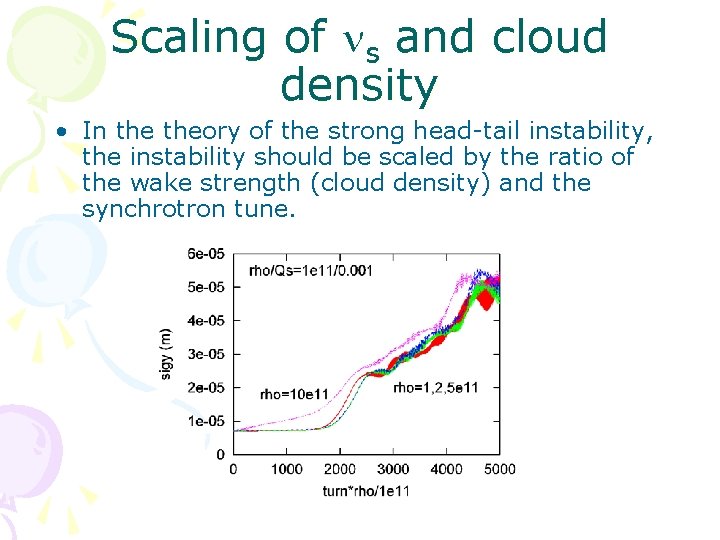
Scaling of ns and cloud density • In theory of the strong head-tail instability, the instability should be scaled by the ratio of the wake strength (cloud density) and the synchrotron tune.

From the results of the PIC simulation (for GLC I) • Threshold of the strong head-tail instability due to the electron cloud is around re/ns =1012/0. 01 m-3. • Growth for re=1012 m-3 is deviated from others, namely the scaling is broken. • Kick due to cloud with the projected density rex C is too strong. The instability occur due to localization of the cloud, and may be not realistic. • For the case that the electron cloud distributes whole of ring, the coherent head-tail instability is dominant.

Summary I • We assume primary electron yield Y 1 g= 6. 6 x 10 -4 and 3. 3 x 10 -4 e-/(m. e+) for GLC damping ring. This value is 1% and 0. 5% of the direct photoelectron yield. • Electron cloud average densities are 0. 8 x 1012 m -3 and 0. 4 x 1012 m-3 for 1% and 0. 5% SR ratio, respectively. • The growth of the coupled bunch instability is 300 ms and 600 ms for 1% and 0. 5% SR ratio, respectively. • The growth can be recovered by bunch feedback.

Summary II • The threshold cloud density of the fast head-tail instability is re=2. 6 x 1012 m-3 for parameter I (ns=0. 01) and re=6. 2 x 1012 m-3 for parameter II (ns=0. 0118) in the linear wake approximation. • The wake approximation neglects some effects: nonlinearity, pinching of electrons… • A PIC simulation has performed to study the effects in detail. • The threshold of the fast head-tail instability was re/ns =1012/0. 01 m-3 for parameter I. It will be higher for parameter II. • It is a factor 2 -3 lower than that of the wake approximation. This discrepancy is due to an ambiguity or accuracy (pinching, choice of Q, coasting beam approximation) of the wake approximation. • Anyway, the threshold is higher than the density of the present estimation based on our model (assumption).