Electron Beams Dose calculation algorithms Kent A Gifford

Electron Beams: Dose calculation algorithms Kent A. Gifford, Ph. D. Department of Radiation Physics UT M. D. Anderson Cancer Center kagifford@mdanderson. org Medical Physics III: Spring 2015

Dose calculation algorithms • Deterministic – Hogstrom pencil beam (Pinnacle 3) – Phase space evolution model – FEM solutions to Boltzmann eqn (Attila)

Dose calculation algorithms Hogstrom pencil beam • Mass scattering power

Dose calculation algorithms Hogstrom pencil beam • Fermi-equation (separated)

Dose calculation algorithms Hogstrom pencil beam • Fermi-equation (solution)

Dose calculation algorithms Hogstrom pencil beam

Discrete Ordinates (FEM)-Attila Linear Boltzmann Transport Equation (LBTE) • Assumptions 1 1. Particles are points 2. Particles travel in straight lines 3. Particles do not interact w each other 4. Collisions occur instantaneously 5. Isotropic materials 6. Mean value of particle density distribution considered • 1 EE Lewis and WF Miller, Computational Methods of Neutron Transport, ANS, 1993.

Fundamentals Linear Boltzmann Transport Equation (LBTE) • ↑direction • ↑Angular • ↑position • ↑particle vector fluence • vector ↑macroscopic energy rate • total extrinsic cross • ↑scattering source section↑ source • Streaming • Collision • Sources • Obeys conservation of particles • Streaming + collisions = production

Fundamentals Linear Boltzmann Transport Equation (LBTE)-angular fluence • • ↑angular fluence rate harmonics • ↑↑angular fluence rate normalized spherical coefficients

Fundamentals Linear Boltzmann Transport Equation (LBTE)-scattering xsection • • ↑differential • orthogonal scattering cross-section Legendre polynomial↑ differential scattering moments ↑

Fundamentals Linear Boltzmann Transport Equation (LBTE)-scattering source • differential • ↑scattering source xsection • angular ↑ fluence rate↑

Fundamentals Linear Boltzmann Transport Equation (LBTE)-Reaction cross-section of type rate↑ • ↑reaction • scalar rate fluence • ↑macroscopic whatever

Fundamentals Attila -Energy approximation • Multi-group approximation • Energy range divided into g, groups • Ordered by decreasing energy • Cross-sections constant w/in group

Fundamentals Attila -Angular approximation • Discrete ordinates method (DOM) • Requires LBTE hold for discrete angles • Angular terms integrated by quadrature set • Mesh swept by each angular ordinate • As # of ordinates , sol’n converges to exact sol’n

Fundamentals Attila -Angular approximation • Discrete ordinates method (DOM)-ray effects • Non-physical buildup in fluence/rate along ordinates • May produce oscillations or negativities • Problematic for localized sources in weakly scattering media

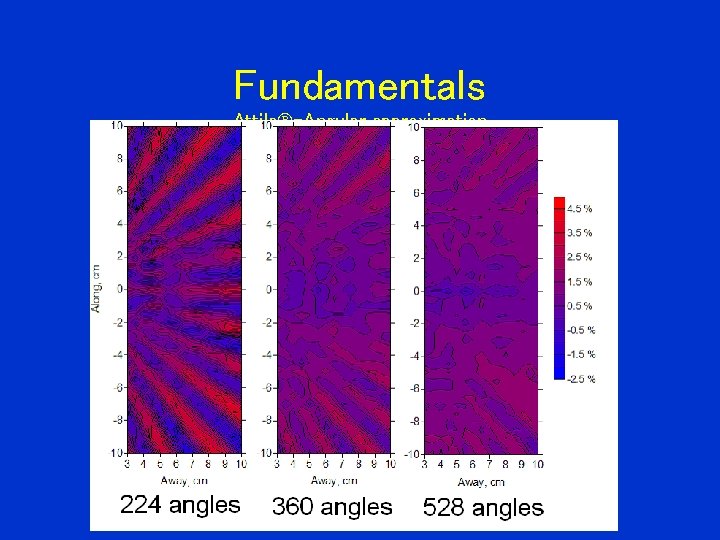
Fundamentals Attila -Angular approximation

Fundamentals Attila -Angular approximation • Ray effect-remedies • Increase # of ordinates • This can be computationally costly • Employ first scatter distributed source (fsds) technique • Less costly since a lower angular order can be used

Fundamentals • FSDS technique Attila -fsds • Separate angular fluence/rate into collided and uncollided components • Ray trace from point source to quadrature or edit points • 1 ST collision source generated at each tet corner • Solve collided angular fluence/rate and add to uncollided

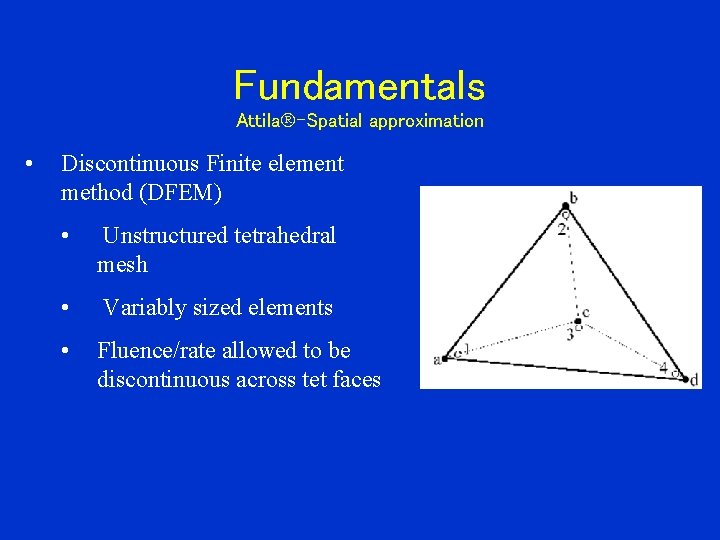
Fundamentals Attila -Spatial approximation • Discontinuous Finite element method (DFEM) • Unstructured tetrahedral mesh • Variably sized elements • Fluence/rate allowed to be discontinuous across tet faces

Fundamentals Attila -Source iteration • Source iteration • 4 Nelements Nordinates Ngroups unknowns • Iteration started with guess for fluence • Process may proceed slowly for problems dominated by scattering • Acceleration technique applied- DSA

Fundamentals Attila -Charged particles • Continuous scattering operator • LBTE • Continuous slowing down operator

Fundamentals Attila -Cross sections • Attila can utilize x-sections from various sources • Multi-group processing codes • NJOY-TRANSX (LANL) • AMPX (ORNL) • CEPXS (SNL)

Pros & Cons of the deterministic method

Pros & Cons Advantages 1. Provides solution for the entire computational domain 2. Mesh based solution lends itself to CT/MRI based geometries 3. Typically more efficient than MC

Dose calculation algorithms Monte Carlo • Stochastic method for evaluating integrals numerically • Generate N random values or points in a space, xi • Calculate the score or tally fi for the N random values, points • Calculate the expectation value, and standard deviation, variance • Rely on central limit theorem • As N approaches infinity, the expectation value will approach reality or true value

Dose calculation algorithms Monte Carlo • Example: • Particle interacting with 2 possibilities • Absorption • Scatter • Random value is particle history or trajectory • Could also tally energy or charge deposition, current, pulses

Dose calculation algorithms Monte Carlo • Algorithm: • Sample random distance to the subsequent interaction site • Transport particle to next interaction factoring in geometry • Choose interaction type based on relative probability • Simulate interaction • Absorption-particle is terminated • Scatter- choose scattering angle using appropriate scattering pdf • Repeat until N histories are simulated

Project • Generate MU calculation program • Any language or spreadsheet program • 12 e-, all field sizes, cones – Verify correct implementation – Demonstrate accuracy on 2 cases

Project 150 c. Gy to 95%, 12 Me. V

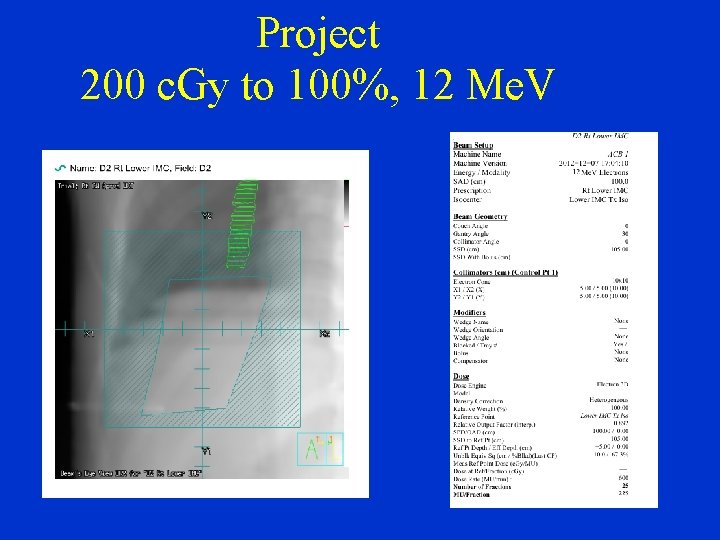
Project 200 c. Gy to 100%, 12 Me. V