Electron and Ion Currents From kinetic theory of

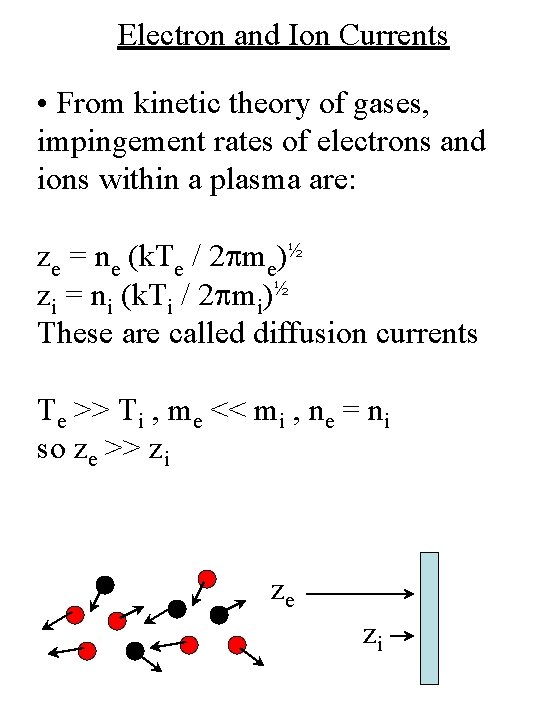
Electron and Ion Currents • From kinetic theory of gases, impingement rates of electrons and ions within a plasma are: ze = ne (k. Te / 2 pme)½ zi = ni (k. Ti / 2 pmi)½ These are called diffusion currents Te >> Ti , me << mi , ne = ni so ze >> zi ze zi

Electron and Ion Currents • For example, ne = ni = 1010 cm-3 Te = 23000 K Ti = 500 K • Then ze = 2. 35 x 1017 cm-2 s-1 Je = eze = 37. 6 m. Acm-2 zi = 1. 28 x 1014 cm-2 s-1 Ji = ezi = 0. 0205 m. Acm-2 Je = 37. 6 m. Acm-2 Ji = 0. 0205 m. Acm-2 Je >> Ji

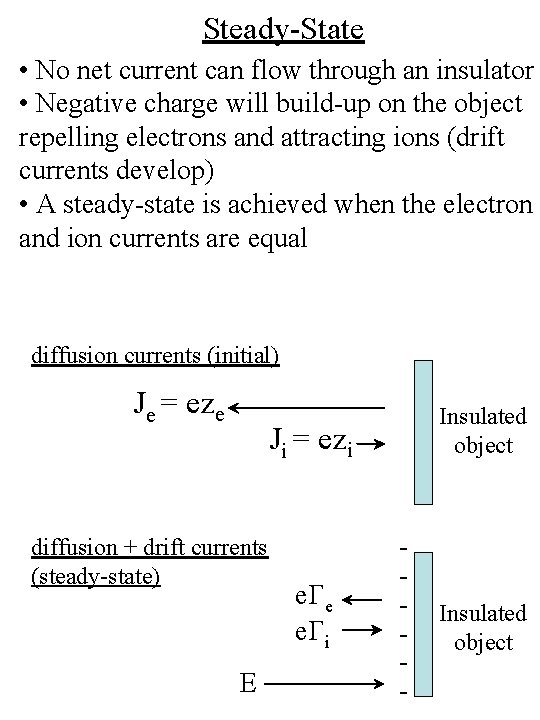
Steady-State • No net current can flow through an insulator • Negative charge will build-up on the object repelling electrons and attracting ions (drift currents develop) • A steady-state is achieved when the electron and ion currents are equal diffusion currents (initial) Je = eze Insulated object Ji = ezi diffusion + drift currents (steady-state) E e. Ge e. Gi - Insulated object

Sheath Region • A positive space-charge region is created that is depleted of electrons, leaving predominantly gas atoms and ions (e. g. , Ar+). • This region is called the sheath region and is similar to the depletion region formed in a semiconductor device such as a p-n junction diode ne - Sheath region Insulated object

Dark Spaces • The sheath regions are also called “dark spaces” due to their visual appearance • Fewer electrons result in less optical emission from Mahan, colorplate VI. 18

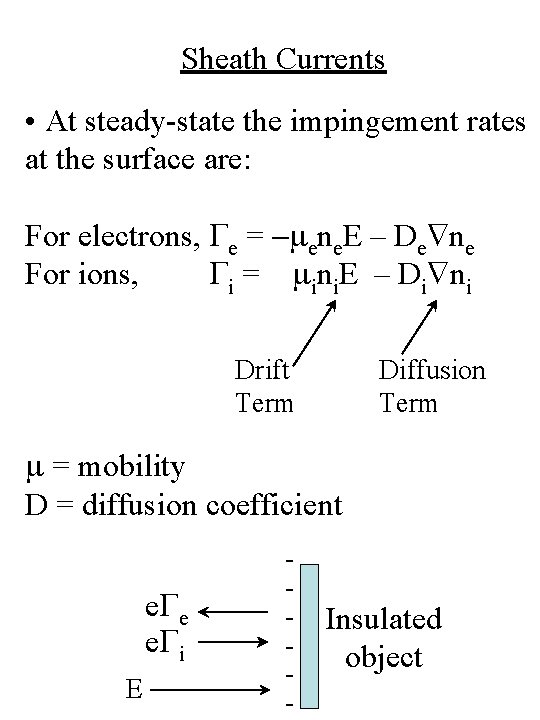
Sheath Currents • At steady-state the impingement rates at the surface are: For electrons, Ge = -mene. E – De ne For ions, Gi = mini. E – Di ni Drift Term Diffusion Term m = mobility D = diffusion coefficient e. Ge e. Gi E - Insulated object

Sheath Currents • In 1 -D, = d/dx, giving: For electrons, Ge = – mene. E – Dedne/dx For ions, Gi = mini. E – Didni/dx • Using ni = ne = n at the edge of the plasma sheath and Ge = Gi (steady-state) gives: – men. E – Dedn/dx = min. E – Didn/dx • Solving for E gives: E = [(dn/dx)/n] [ (Di – De) / (mi + me) ] e. Ge e. Gi E - Insulated object

Sheath Currents • Substituting this expression for E into the ion flux equation gives: Gi = – Da dni/dx Da = (mi. De + me. Di)/(me + mi) (ambipolar diffusion coefficient) Since me >> mi, we have Da = Di + (mi/me)De

Sheath Currents • Next we can use the Einstein relation between mobility and diffusion, D/m = k. T/q, to give: Da = Di (1 + Te / Ti) Since Te >> Ti, we have Da = Di. Te/Ti We see that Da >> Di

Sheath Currents • The effect of the electrons is to establish an electric field that pulls the ions and increases it’s effective diffusion from Di (the unaided diffusion at E = 0) to Da • This effect is known as ambipolar diffusion e. Ge e. Gi E - Insulated object

Sheath Currents • The ion current increases to Gi ~ ni √(k. Te/mi) • For example, for ni = 1010 cm-3, Te = 23000 K, and Ar gas, we have Gi = 2 x 1015 cm-2 s-1 e. Gi = 0. 35 m. A/cm 2 • The enhanced ion current is much greater than the unaided diffusive flux calculated previously (ezi = 0. 0205 m. Acm-2) • Gi ~ surface atom density in 1 sec

Growth Rate Example Gi ~ 1 m. Acm-2 = 6. 2 x 1015 ions s-1 cm-2 Y (1 ke. V Ar+ ions on Al) ~ 1. 5 Sputter rate of Al = 9. 3 x 1015 atoms cm-2 s-1 Surface density of Al = 6. 07 x 1022 atoms cm-3 The deposition rate would be 15 Å s-1 = 5. 4 mm/hr

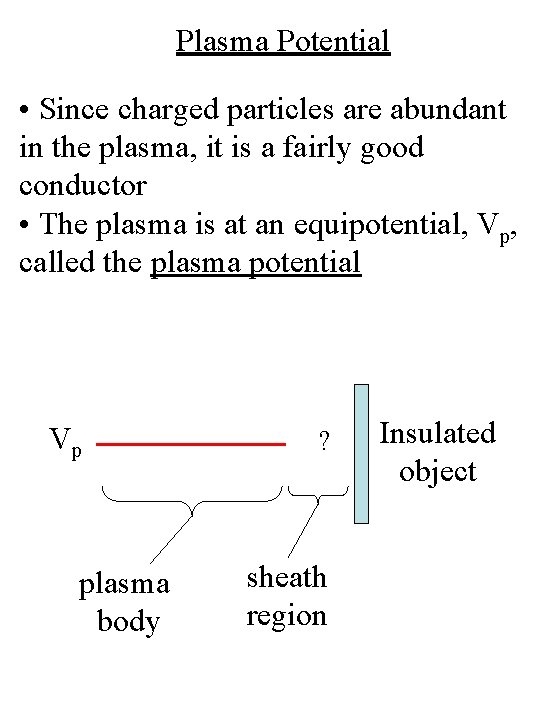
Plasma Potential • Since charged particles are abundant in the plasma, it is a fairly good conductor • The plasma is at an equipotential, Vp, called the plasma potential Vp plasma body ? sheath region Insulated object

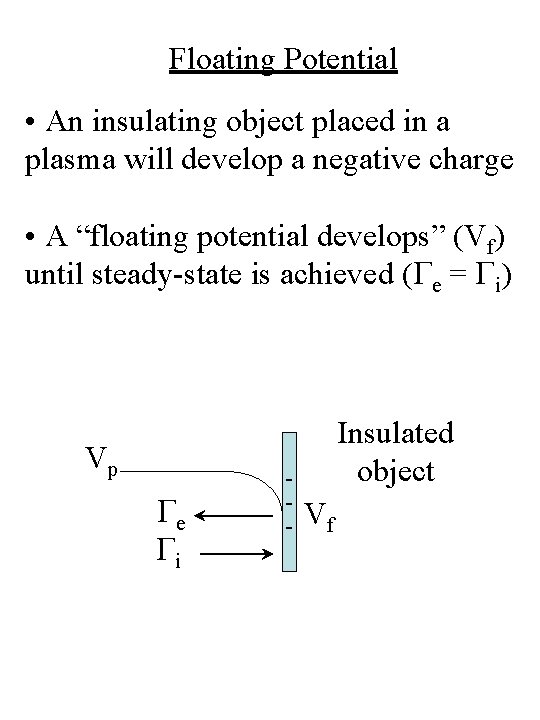
Floating Potential • An insulating object placed in a plasma will develop a negative charge • A “floating potential develops” (Vf) until steady-state is achieved (Ge = Gi) Vp Ge Gi - Insulated object Vf

Floating Potential Vp Ge Gi - Insulated object Vf • M-B distribution of energies: Gi = Ge = ze exp [ -e (Vp – Vf)/k. Te ] • Rearranging gives Vp – Vf = (k. Te/e) ln ( ze / Gi ) = (k. Te/2 e)ln(mi/2 pme) • e. g. , if Te = 23000 K, eze = 37. 6 m. Acm-2, and e. Gi = 0. 35 m. Acm-2 as calculated previously then Vp – Vf = 9. 3 V

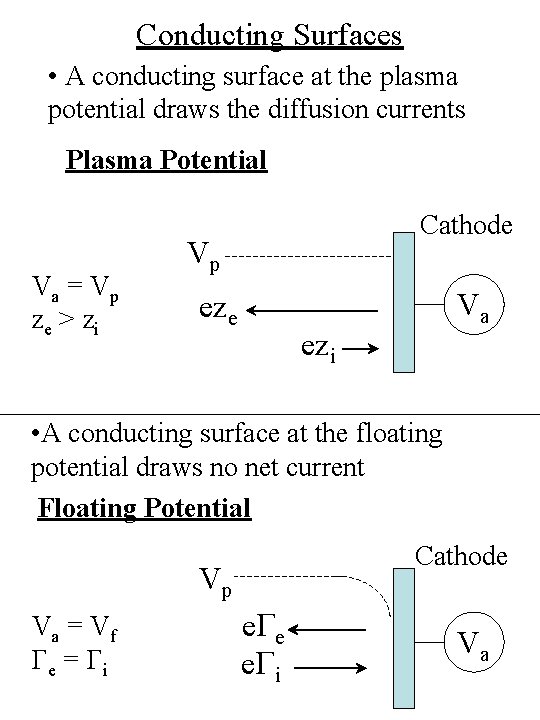
Conducting Surfaces • A conducting surface at the plasma potential draws the diffusion currents Plasma Potential Va = Vp ze > zi Cathode Vp eze Va ezi • A conducting surface at the floating potential draws no net current Floating Potential Cathode Vp Va = Vf Ge = Gi e. Ge e. Gi Va

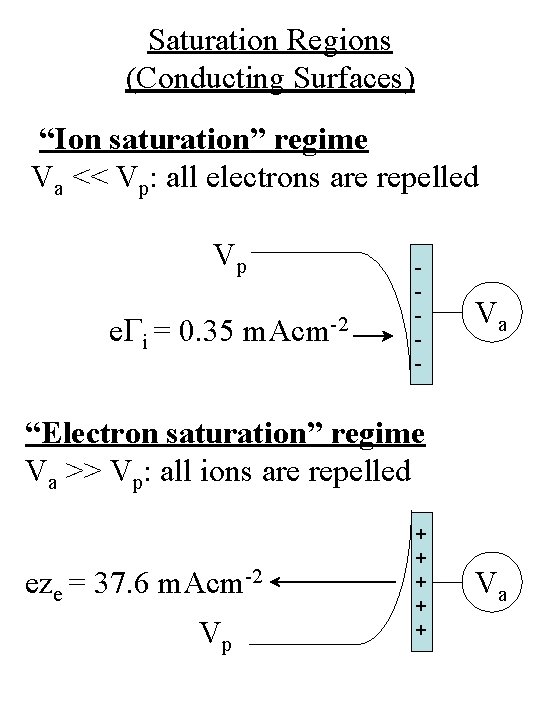
Saturation Regions (Conducting Surfaces) “Ion saturation” regime Va << Vp: all electrons are repelled Vp e. Gi = 0. 35 m. Acm-2 - Va “Electron saturation” regime Va >> Vp: all ions are repelled eze = 37. 6 m. Acm-2 V p + + + Va

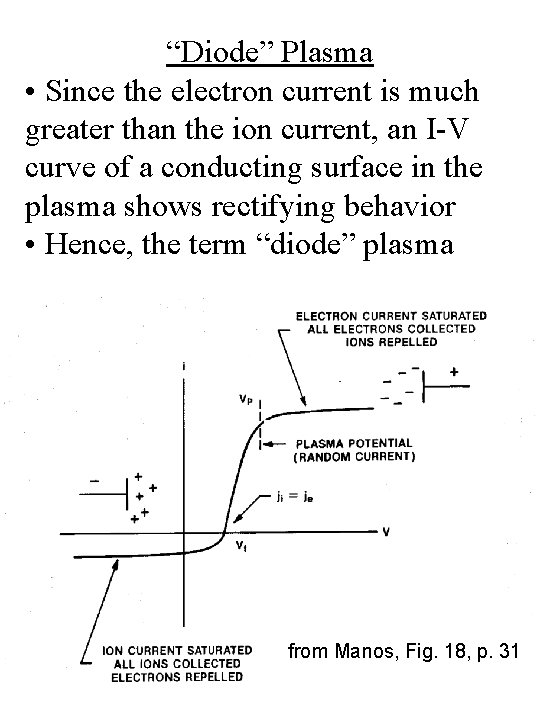
“Diode” Plasma • Since the electron current is much greater than the ion current, an I-V curve of a conducting surface in the plasma shows rectifying behavior • Hence, the term “diode” plasma from Manos, Fig. 18, p. 31

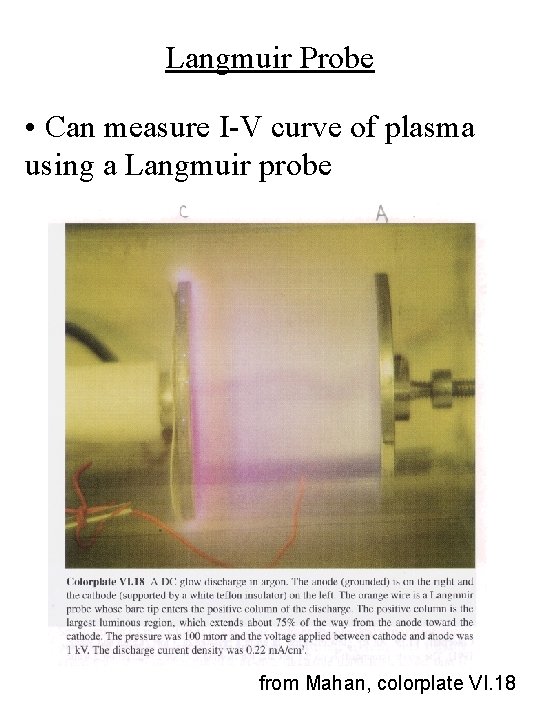
Langmuir Probe • Can measure I-V curve of plasma using a Langmuir probe from Mahan, colorplate VI. 18

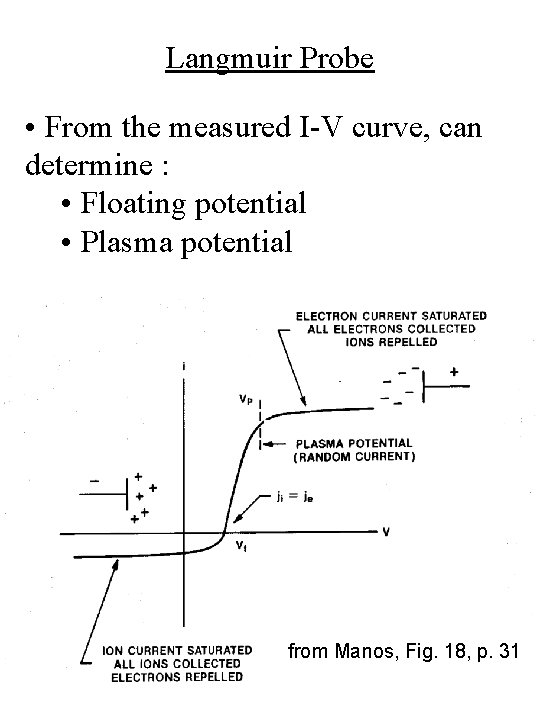
Langmuir Probe • From the measured I-V curve, can determine : • Floating potential • Plasma potential from Manos, Fig. 18, p. 31

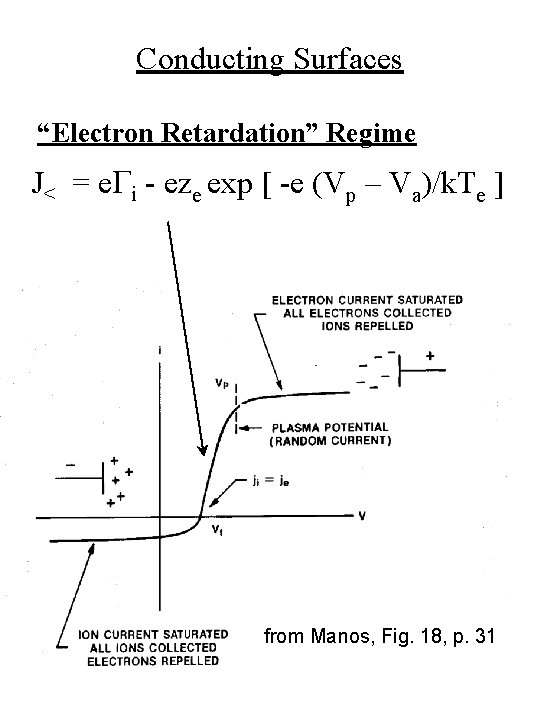
Conducting Surfaces “Electron Retardation” Regime J< = e. Gi - eze exp [ -e (Vp – Va)/k. Te ] from Manos, Fig. 18, p. 31

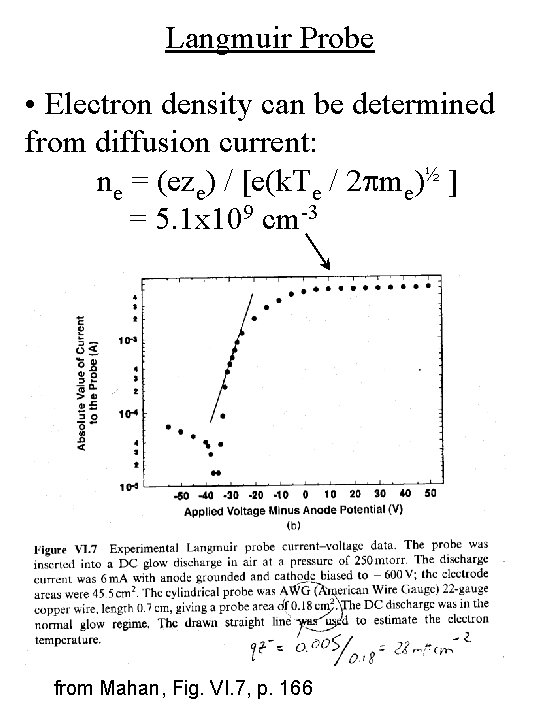
Langmuir Probe • Electron temperature, Te ~ e / [ k dln(J)/d. V ] = 47 840 K from Mahan, Fig. VI. 7, p. 166

Langmuir Probe • Electron density can be determined from diffusion current: ne = (eze) / [e(k. Te / 2 pme)½ ] = 5. 1 x 109 cm-3 from Mahan, Fig. VI. 7, p. 166

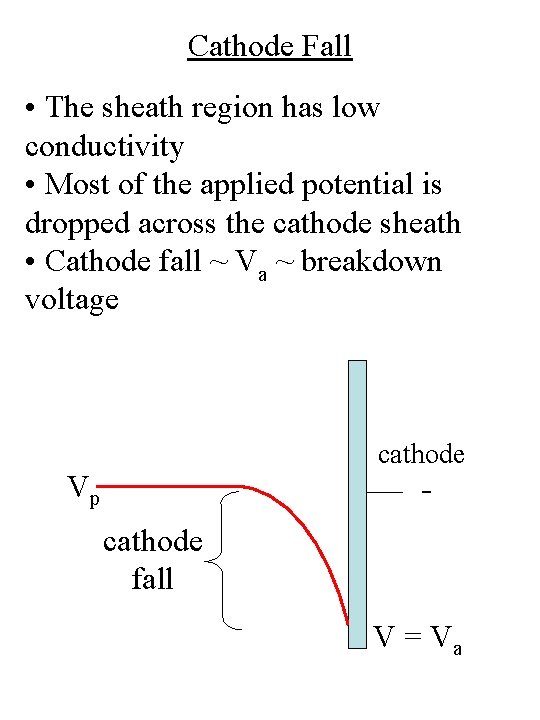
Cathode Fall • The sheath region has low conductivity • Most of the applied potential is dropped across the cathode sheath • Cathode fall ~ Va ~ breakdown voltage cathode Vp cathode fall V = Va

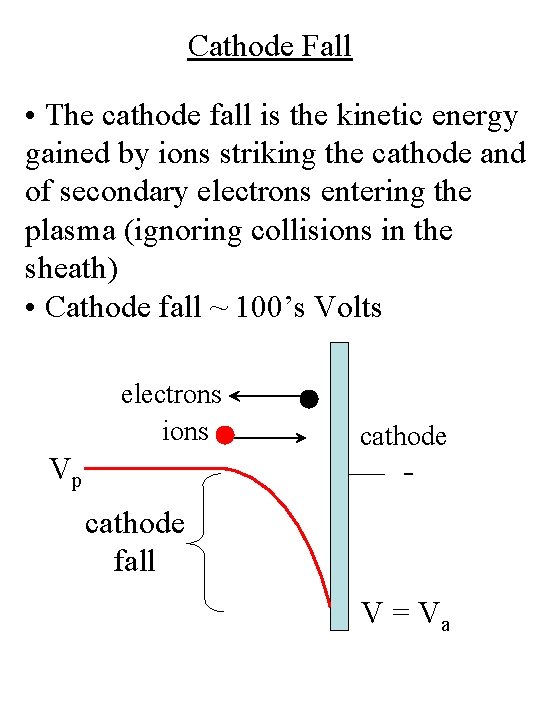
Cathode Fall • The cathode fall is the kinetic energy gained by ions striking the cathode and of secondary electrons entering the plasma (ignoring collisions in the sheath) • Cathode fall ~ 100’s Volts electrons ions Vp cathode fall V = Va

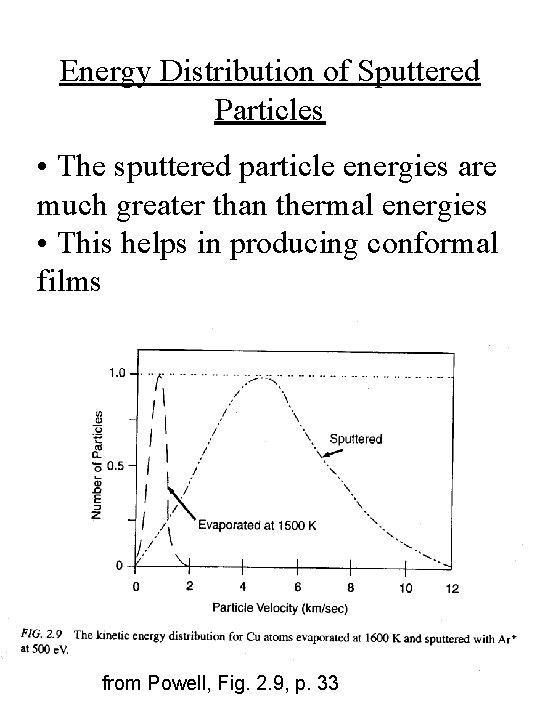
Energy Distribution of Sputtered Particles • The sputtered particle energies are much greater than thermal energies • This helps in producing conformal films from Powell, Fig. 2. 9, p. 33

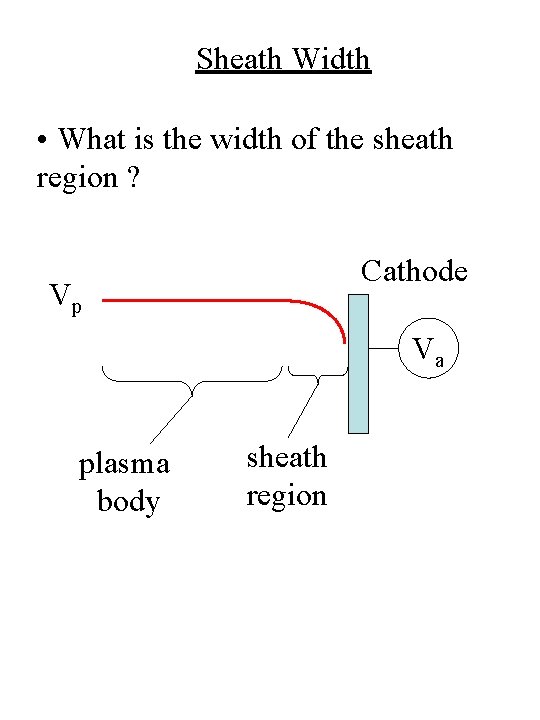
Sheath Width • What is the width of the sheath region ? Cathode Vp Va plasma body sheath region

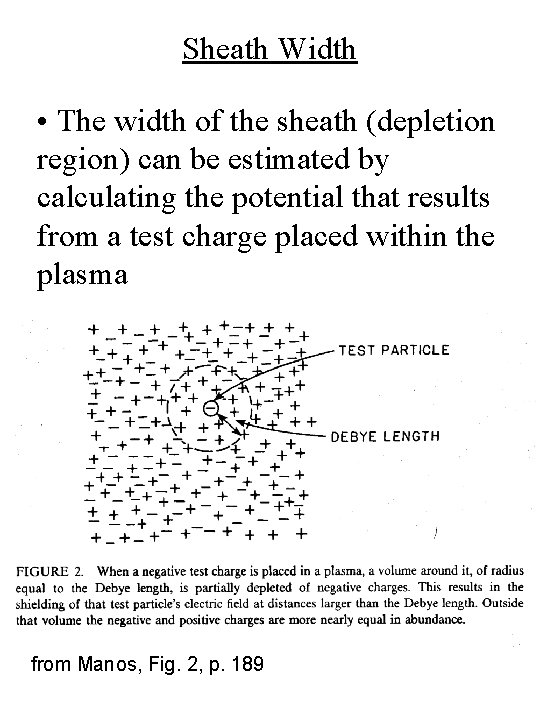
Sheath Width • The width of the sheath (depletion region) can be estimated by calculating the potential that results from a test charge placed within the plasma from Manos, Fig. 2, p. 189

Sheath Width • The charge creates a potential, which in free space (no plasma) would be: Vo(r) = e / (4 peor) r = distance from the test charge

Sheath Width • The potential in the plasma may be determined by solving Poisson’s equation: 2 V(r) = – r(r)/eo 2 = Laplacian operator

Sheath Width r(r) = local charge density = e [ ni(r) – ne(r) ] Boltzmann’s law: ne(r) = ne exp [ e. V(r) / k. Te ] ~ ne [ 1 + e. V(r) / k. Te ] ni(r) ~ ni since ions are too slow to respond relative to the electrons ni, ne = n = plasma density r(r) ~ – (e 2 n/k. Te) V(r)

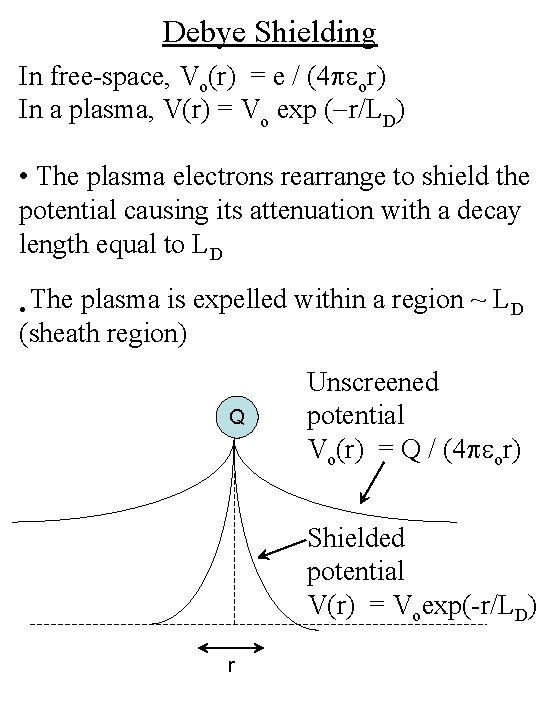
Debye Length 2 V(r) = - (e 2 n/eok. Te) V(r) Solving gives, V (r) = Vo exp (-r/LD) LD = Debye length = (eok. Te / e 2 n)½

Debye Shielding In free-space, Vo(r) = e / (4 peor) In a plasma, V(r) = Vo exp (-r/LD) • The plasma electrons rearrange to shield the potential causing its attenuation with a decay length equal to LD • The plasma is expelled within a region ~ LD (sheath region) Q Unscreened potential Vo(r) = Q / (4 peor) Shielded potential V(r) = Voexp(-r/LD) r

Debye Length LD = Debye length = (eok. Te/e 2 n)½ = 6. 93 [ Te(K) / ne (cm-3) ] ½ = 743 [ Te(e. V) / ne(cm-3) ] ½ • For example, for Te = 1 e. V, ne = 1010 cm-3, we get LD = 74 mm

Child’s Law A more exact treatment for a planar surface (cathode) gives: Ls = (4 eo/9 e. Ga)½(2 e/mi)¼(Vp-Va)¾ Substituting Gi as determined previously gives: Ls ~ 0. 8 ¾ LD = e(Vp - Va)/ k. Te · Hence, the sheath thickness is on the order of 10’s of LD (mm’s) · Electrode spacing ~ cm’s

Cathode Fall from Mahan, colorplate VI. 18

Plasma Reactions Homogeneous Reactions (occur within the plasma) Heterogeneous Reactions (occur on a surface)

Homogeneous Reactions • Reactions that occur within the plasma Excitation : • Electrons produce vibrational, rotational, and electronic states leaving the atom or molecule in an excited state e- + O 2* e- + Ar* e- + O* Glow discharge: O 2* O 2 + hn O* O + hn

Homogeneous Reactions Ionization : • Responsible for ion & electron formation which sustains the plasma • Produces ions for sputtering e- + Ar Ar+ + 2 ee- + O 2+ + 2 e-

Homogeneous Reactions Dissociation : • A molecule is broken into smaller atomic or molecular fragments (radicals) that are generally much more chemically active than the parent molecule • This is important in reactive sputtering (e. g. , reactive ion etching) and plasma-enhanced CVD e- + O 2 O + ee- + CF 4 e- + CF 3* + F*

Heterogeneous Reactions • Reactions that occur on the surface • Sputtering • Secondary electron emission • Reactive etching/deposition

Reactive Ion Sputtering (Deposition) • Excited species (particularly radicals) can react with the surface to deposit nitrides and oxides Reactive sputter deposition : From Ohring, p. 126

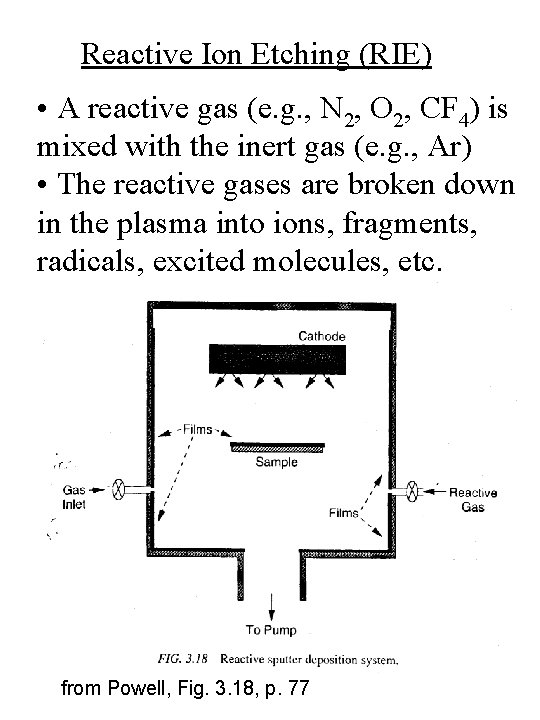
Reactive Ion Etching (RIE) • A reactive gas (e. g. , N 2, O 2, CF 4) is mixed with the inert gas (e. g. , Ar) • The reactive gases are broken down in the plasma into ions, fragments, radicals, excited molecules, etc. from Powell, Fig. 3. 18, p. 77

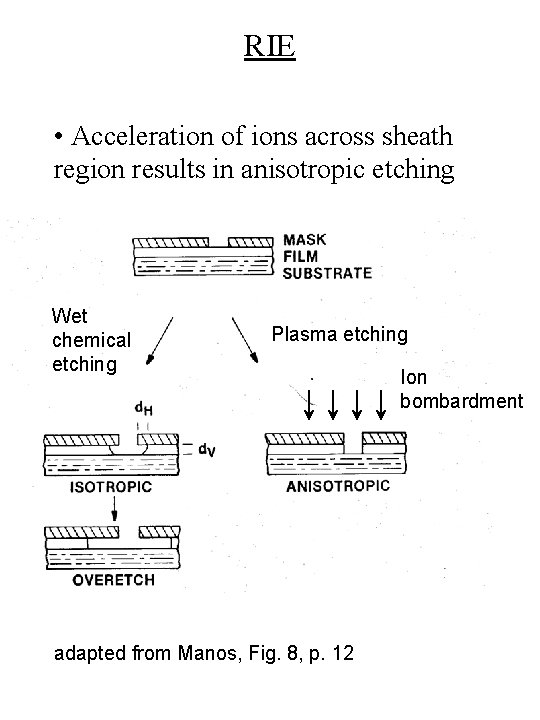
RIE • Acceleration of ions across sheath region results in anisotropic etching Wet chemical etching Plasma etching adapted from Manos, Fig. 8, p. 12 Ion bombardment