Electromagnetic Field Introduction to Electromagnetic Fields Electric Fields














- Slides: 15

Electromagnetic Field

Introduction to Electromagnetic Fields Electric Fields: * Electric fields are created by differences in voltage: the higher the voltage, the stronger will be the resultant field. n Magnetic Field: *Magnetic fields are created when electric current flows: the greater the current, the stronger the magnetic field. n An electric field will exist even when there is no current flowing. n If current does flow, the strength of the magnetic field will vary with power consumption but the electric field strength will be constant. n Lecture 2

Introduction to Electromagnetic Fields n Electromagnetic Field * Electromagnetic fields are a combination of invisible electric and magnetic fields of force. * They are generated by natural phenomena like the Earth’s magnetic field but also by human activities, through the use of electricity. * Electromagnetic waves: waves excited by charges in time -varying motion Lecture 2

Introduction to Electromagnetic Fields Examples: *Mobile phones, power lines and computer screens are examples of equipment that generates electromagnetic fields. n Electromagnetics It is the study of the effect of charges at rest and charges in motion. n Some special cases of electromagnetics: - Electrostatics: charges at rest - Magnetostatics: charges in steady motion (DC) n Natural sources of electromagnetic fields: -. electrical charges. thunderstorm Lecture 2 n Human-made sources of electromagnetic fields: -. X-rays n

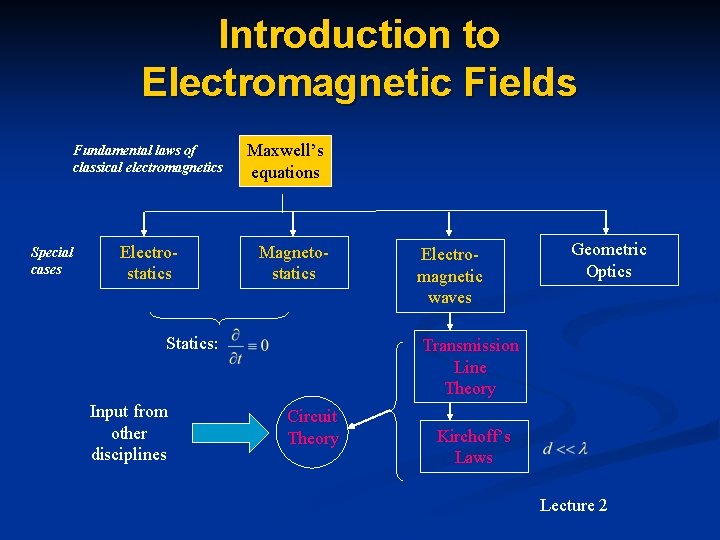
Introduction to Electromagnetic Fields Fundamental laws of classical electromagnetics Special cases Electrostatics Maxwell’s equations Magnetostatics Statics: Input from other disciplines Electromagnetic waves Geometric Optics Transmission Line Theory Circuit Theory Kirchoff’s Laws Lecture 2

Introduction to Electromagnetic Fields • transmitter and receiver are connected by a “field. ” Lecture 2

Introduction to Electromagnetic Fields n When an event in one place has an effect on something at a different location, we talk about the events as being connected by a “field”. n A field is a spatial distribution of a quantity; in general, it can be either scalar or vector in nature. Lecture 2

Introduction to Electromagnetic Fields n Electric and magnetic fields: n Are vector fields with three spatial components. n Vary as a function of position in 3 D space as well as time. n Are governed by partial differential equations derived from Maxwell’s equations. Lecture 2

Introduction to Electromagnetic Fields n A scalar is a quantity having only an amplitude (and possibly phase). Examples: voltage, current, charge, energy, temperature n A vector is a quantity having direction in addition to amplitude (and possibly phase). Examples: velocity, acceleration, force Lecture 2

Introduction to Electromagnetic Fields n Fundamental vector field quantities in electromagnetics: n Electric field intensity units = volts per meter (V/m = kg m/A/s 3) n Electric flux density (electric displacement) units = coulombs per square meter (C/m 2 = A s /m 2) n Magnetic field intensity units = amps per meter (A/m) n Magnetic flux density units = teslas = webers per square meter (T = Wb/ m 2 ) Lecture 2

Introduction to Electromagnetic Fields n Relationships involving the universal constants: In free space: Lecture 2

Introduction to Electromagnetic Fields n Universal constants in electromagnetics: n Velocity of an electromagnetic wave (e. g. , light) in free space (perfect vacuum) n Permeability of free space n Permittivity of free space: n Intrinsic impedance of free space: Lecture 2

Maxwell’s Equations n n n Maxwell’s equations in integral form are the fundamental postulates of classical electromagnetics - all classical electromagnetic phenomena are explained by these equations. Electromagnetic phenomena include electrostatics, magnetostatics, electromagnetostatics and electromagnetic wave propagation. The differential equations and boundary conditions that we use to formulate and solve EM problems are all derived from Maxwell’s equations in integral form. Lecture 2

Maxwell’s Equations n Various equivalence principles consistent with Maxwell’s equations allow us to replace more complicated electric current and charge distributions with equivalent magnetic sources. n These equivalent magnetic sources can be treated by a generalization of Maxwell’s equations. Lecture 2

Maxwell’s Equations in Integral Form (Generalized to Include Equivalent Magnetic Sources) Adding the fictitious magnetic source terms is equivalent to living in a universe where magnetic monopoles (charges) exist. Lecture 2