Electrolytic dissociation of water The water molecules dissociates

Electrolytic dissociation of water The water molecules dissociates according to the reaction: H 2 O + H 2 O H 3 O+ + HO- The equilibrium is shifted far to the left. Experimentally, it was determined that at 25°C, only one molecule of water, out of 556, 000 is dissociated, which means the dissociation degree of water is α = 18· 10 -10. The equilibrium constant for the dissociation reaction of water is: 1

Kw is called the ionic product of water The ionic product of water depends on the temperature. At 25°C, the value of KW is 10 -14 mol L-1. In pure water the concentration of the H 3 O+ ions is equal to that of the HO-, which means that at 25°C: mol L-1 2

To express the concentration of the hydrogen ions in aqueous solutions, the notion of p. H was introduced by Sörensen (1909): The relation was modified by Bates by replacing the concentration of the hydronium ions with their activity: or For diluted solutions, the activity can be considered equal to the concentration 3

Similar to the p. H notion the term of p. OH was introduced, that is a measure of the concentration of the hydroxyl ions: It is easily demonstrated that, at the temperature of 25°C: p. H + p. OH = -lg KW = 14 4

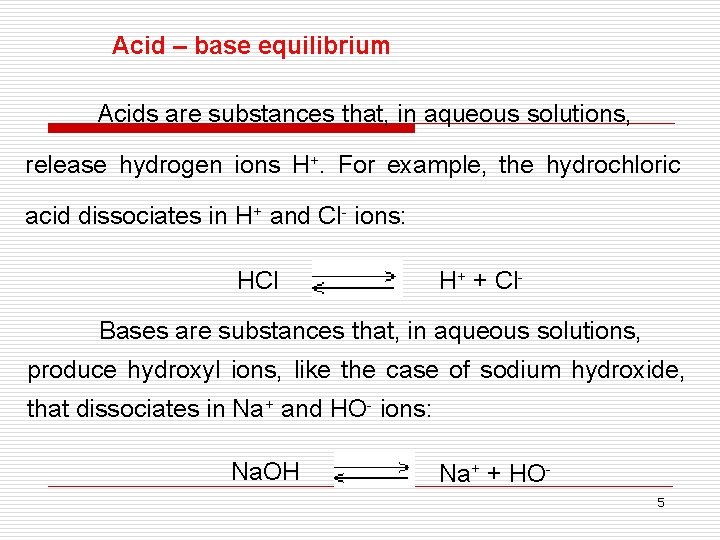
Acid – base equilibrium Acids are substances that, in aqueous solutions, release hydrogen ions H+. For example, the hydrochloric acid dissociates in H+ and Cl- ions: HCl H+ + Cl- Bases are substances that, in aqueous solutions, produce hydroxyl ions, like the case of sodium hydroxide, that dissociates in Na+ and HO- ions: Na. OH Na+ + HO 5

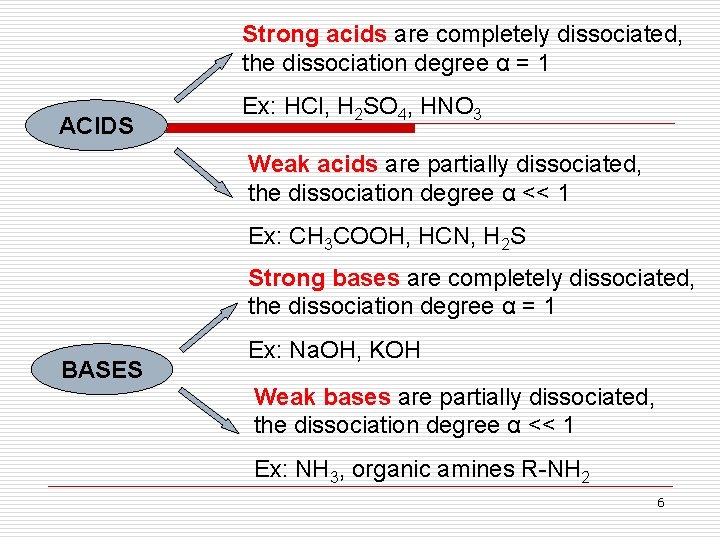
Strong acids are completely dissociated, the dissociation degree α = 1 ACIDS Ex: HCl, H 2 SO 4, HNO 3 Weak acids are partially dissociated, the dissociation degree α << 1 Ex: CH 3 COOH, HCN, H 2 S Strong bases are completely dissociated, the dissociation degree α = 1 BASES Ex: Na. OH, KOH Weak bases are partially dissociated, the dissociation degree α << 1 Ex: NH 3, organic amines R-NH 2 6

The dissociation degree is defined as the ratio between the number of dissociated molecules and the total number of dissolved molecules: 7

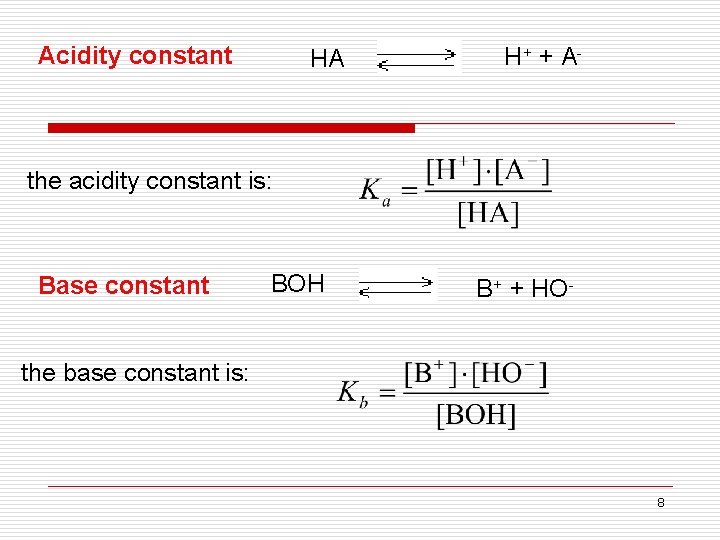
Acidity constant HA H+ + A - the acidity constant is: Base constant BOH B+ + HO- the base constant is: 8

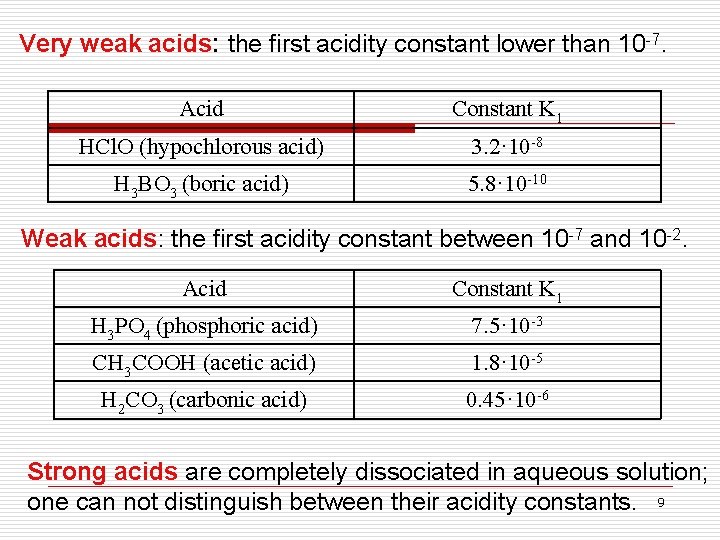
Very weak acids: the first acidity constant lower than 10 -7. Acid Constant K 1 HCl. O (hypochlorous acid) 3. 2· 10 -8 H 3 BO 3 (boric acid) 5. 8· 10 -10 Weak acids: the first acidity constant between 10 -7 and 10 -2. Acid Constant K 1 H 3 PO 4 (phosphoric acid) 7. 5· 10 -3 CH 3 COOH (acetic acid) 1. 8· 10 -5 H 2 CO 3 (carbonic acid) 0. 45· 10 -6 Strong acids are completely dissociated in aqueous solution; one can not distinguish between their acidity constants. 9

Weak bases, like ammonia, aniline, have the base constant below 10 -3: Base Constant Kb Ammonia NH 3 1. 7· 10 -5 Aniline C 6 H 5 – NH 2 3. 8· 10 -10 Strong bases, like sodium hydroxide, calcium hydroxide, are completely dissociated in water, like in case of strong acids, one can not distinguish between their base constants. 10

Calculation of p. H for acid and base solutions Strong acids are completely dissociated in aqueous solutions so the hydronium ions concentration is equal to the concentration of the acid. For example, for a 10 -3 mol L-1 solution of HCl, the concentration of the hydronium ions is [H 3 O+] = 10 -3 mol L-1. The p. H of the solution is: p. H = -lg[H+] = -lg 10 -3 = 3 For a strong base, for example 10 -3 mol L-1 KOH the concentration of hydroxyl ions is [HO-] = 10 -3 mol L-1. It results that the p. OH of the solution is: p. OH = -lg[HO-] = -lg 10 -3 = 3 Considering the relation between p. OH and p. H one obtains: p. H = 14 – p. OH = 14 – 3 = 11 11

For concentrations higher than 10 -3 mol L-1 the p. H is calculated using the Bates relation because the activity differs from the concentration At very low acid concentrations to calculate p. H it is necessary to consider the hydronium ions coming from the dissociation of both acid as well as water molecule. 12

For example, the p. H of a 10 -7 mol L-1 solution of HCl is not 7 because the hydronium ions result not only from the dissociation of the acid, but from the dissociation of water as well: HCl H+ + Cl- H 2 O H+ + HO- Considering that the concentration of hydrochloric acid in the solution is c = 10 -7 and the concentration of hydronium, respectively hydroxyl ions is x, the total hydronium ions concentration will be c+x. The ionic product of water, at the temperature of 25°C, will be: (x + c)x = 10 -14 13

One obtains a second degree equation: x 2 + cx - 10 -14 = 0 Solving the equation one obtains: =6. 18 10 -8 The solution with “minus” in front of the square root has no meaning, since it is negative. The concentration of the hydronium ions will be: [H+] = 10 -7 + 6, 18 10 -8 = 1. 618 10 -7 Thus, the p. H of a 10 -7 mol L-1 solution of HCl, will be: p. H = -lg[H 3 O+] = -lg 1. 618 10 -7 = 6. 79 14