Electricity Ohms Law Potential Difference V If a

Electricity Ohm’s Law

Potential Difference (V) • If a charged object is in an electric field it has electric potential energy, that is it has the potential to move in that field. • Potential Difference- represents the amount of work required to move one coulomb of charge from point A to point B • Also called the electromotive force (the force that moves electrons), and voltage. • Measured in Volts or Joules/Coulomb

Electric Current (I) • • • The flow of charged particles, caused by a difference in electric potential. CONVENTIONAL Current Defined in terms of the moving of a positive charge But…. Electrons travels from negative to positive terminals Vector Measured in amperes (A) or C/s

Current I = q t q = the amount of charge in Coulombs that passes a point when a current of one ampere flows for 1 second

Example • Calculate the current if a charge of 5. 60 C passes through a point in a conductor in 15. 4 s. • • • q=5. 60 C t=15. 4 s I=? I=Δq/t I=5. 6/15. 4 I=0. 36 A

Resistance (R) • The amount of electric potential needed to force a given amount of current through an object • Or the opposition a device or conductor offers to the flow of electric current • Scalar • Measured in ohms (Ω) • Or Volts/Amp

Ohm’s Law • Ohm’s Law states that an object has an ability to resist electric current flowing through it. The more resistance an object has, the more voltage you need to force electric current through it. Or, for a given voltage, the more resistance an object has, the less current will flow through it. • V=IR • V=Voltage (volts) • I=Current (amperes) • R=Resistance (ohms)

Example • What is the potential difference across a conductor to produce a current of 8. 00 A if there is a resistance in the conductor of 12. 0 Ω? • I=8 Amps • R=12 Ω • V=? • V=IR • V=8(12) • V=96 V

Power (P) • The rate that work is done on a charged particle in an electric field • Measured in watts or joules/second or Amp*Volts • P=IV • P=power (watts) • I=current (amps) • V=voltage (volts)

Units for Power • Electric Power is normally measured in kilowatt-hour • To convert watts to kilowatt-hour multiple by the number of hours and divide by 1000 • 500 watts in 8 hours would be • (500 x 8)/1000=4 k. Wh

Example • What is the power when a current of 30 amps flows through a wire with a resistance of 3 ohms? • I=30 A • R=3 Ω • P=? • P=IV • V? • V=IR • V=30 (3) • V=90 V • P=30(90) • P=2700 W

Conductivity • A property of a material that depends on the availability of charges that are relatively free to move under the influence of an electric field • All materials have different conductivity • Metals have many electrons that are free to move-good conductors • Nometals electrons are tightly bound-good insulators

Resistance • Depends on • Length • Directly Proportional • Thickness • Indirectly Proportional • Temperature • Directly Proportional

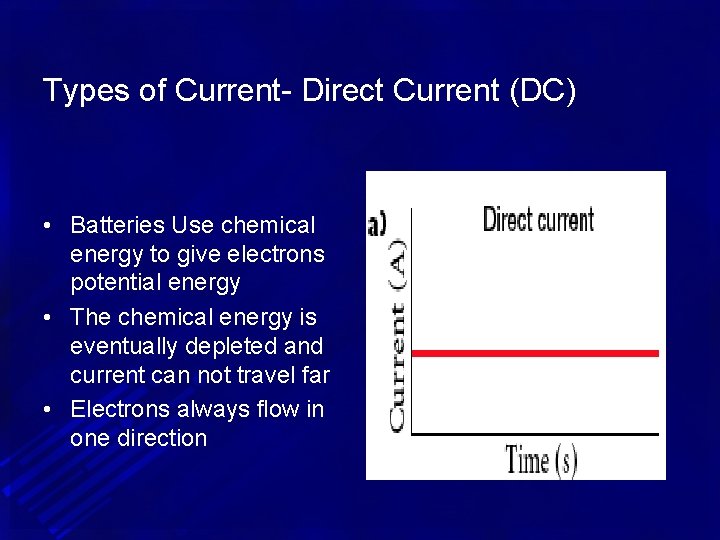
Types of Current- Direct Current (DC) • Batteries Use chemical energy to give electrons potential energy • The chemical energy is eventually depleted and current can not travel far • Electrons always flow in one direction

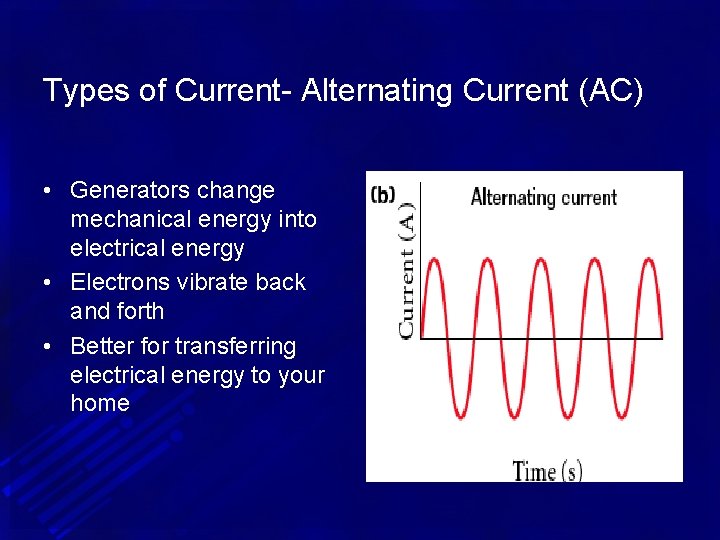
Types of Current- Alternating Current (AC) • Generators change mechanical energy into electrical energy • Electrons vibrate back and forth • Better for transferring electrical energy to your home

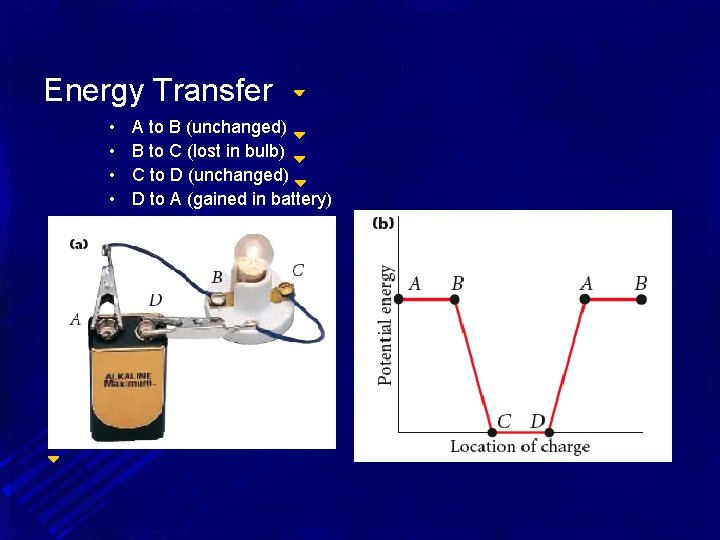
Energy Transfer • Is the electrical potential energy gained, lost, or unchanged as the electrons flow through the following portions of the circuit shown: • • A to B B to C C to D D to A • Explain your answers.

Energy Transfer • • A to B (unchanged) B to C (lost in bulb) C to D (unchanged) D to A (gained in battery)

Electricity Introduction on Circuits

Electric Circuit • A set of electrical components connected such that they provide one or more complete paths for the movement of charges. • A schematic diagram or circuit diagrams can be used to show a circuit • A circuit MUST contain an energy source (EMF), and a pathway for the electrons to flow (wire/conductor)

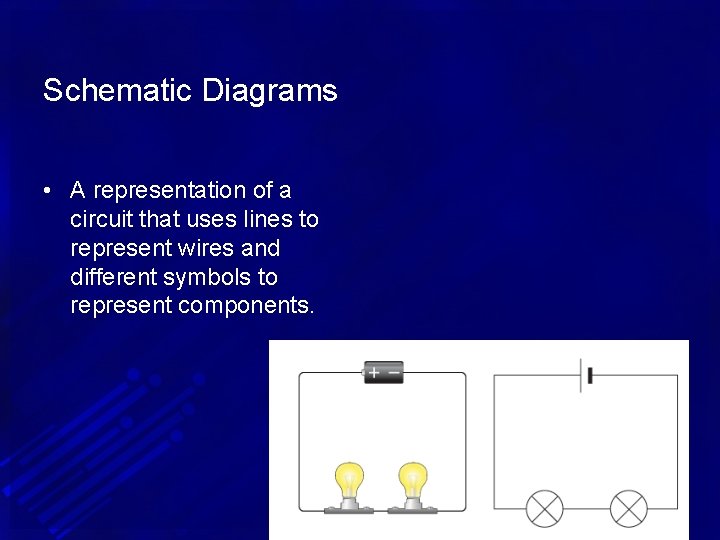
Schematic Diagrams • A representation of a circuit that uses lines to represent wires and different symbols to represent components.

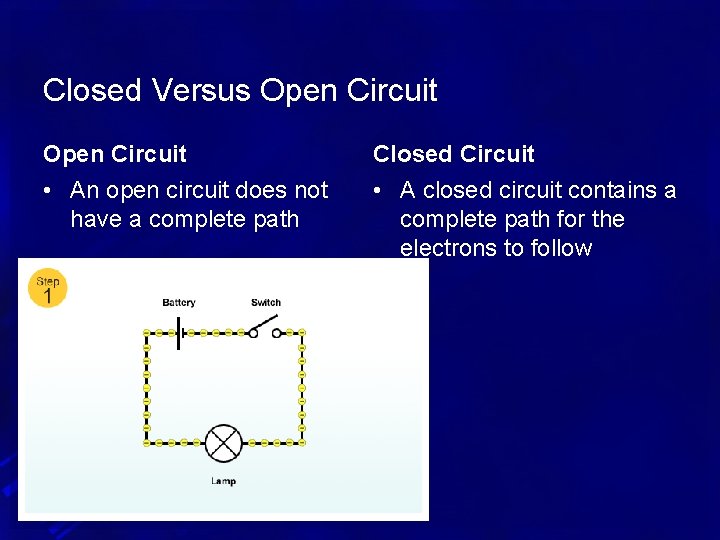
Closed Versus Open Circuit Closed Circuit • An open circuit does not have a complete path • A closed circuit contains a complete path for the electrons to follow

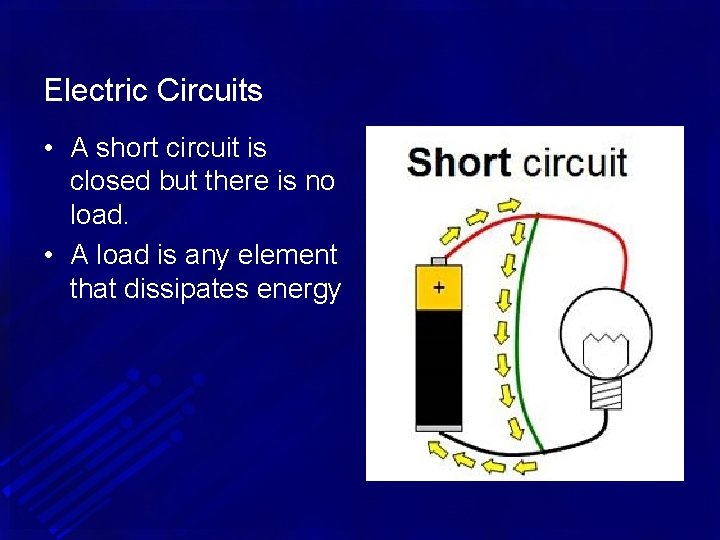
Electric Circuits • A short circuit is closed but there is no load. • A load is any element that dissipates energy

What Does a Load Do?

Series Circuit Versus Parallel Circuit Series Parallel • Two or more components of a circuit which provide a single path for current • Two or more components of a circuit which provide multiple paths for current

Electricity More on Series Circuits

Series Circuit • A circuit in which there are two or more components in which the current has only ONE path • If resistors are in a series then the total resistance is equal to the sum of all of the resistances • Rt=R 1 + R 2 + R 3…. .

Example Resistors in Series A 9. 0 V battery is connected to four light bulbs, as shown at right. Find the equivalent resistance for the circuit.

Example Continued Resistors in Series 1. Define Given: ∆V = 9. 0 V R 1 = 2. 0 Ω R 2 = 4. 0 Ω R 3 = 5. 0 Ω R 4 = 7. 0 Ω Unknown: Req = ? Diagram:

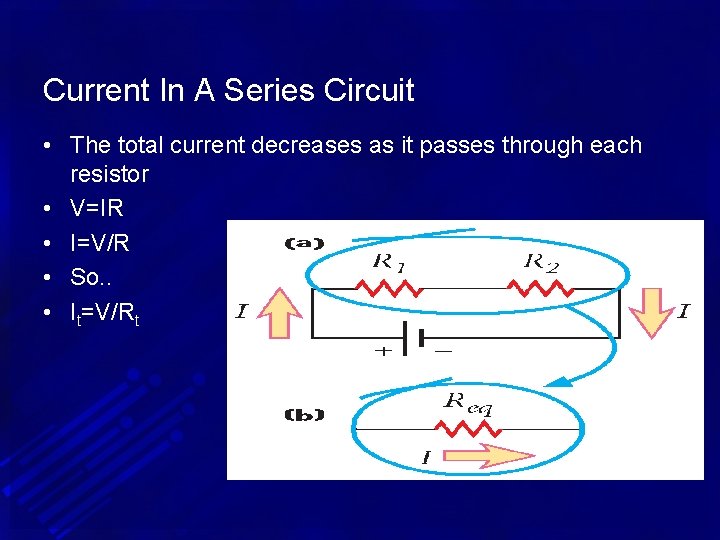
Current In A Series Circuit • The total current decreases as it passes through each resistor • V=IR • I=V/R • So. . • It=V/Rt

Example Continued • Go back to the last example, find the current that runs through the circuit • V=9 V • Rt=18 Ω • It=? • It=V/Rt • It=9/18 • It=. 5 A

Current In A Series Circuit Continued • If a circuit is a series, then a break in the circuit effects all of the components • What would happen if the 2. 0 ohm resistor were disconnected? • Burnt out?

Kirchoff’s Laws/Ohm’s Law for Series Circuits • There is only one path so the current must be the same everywhere in a series circuit • I t= I 1 = I 2 = I 3 … • The total voltage across the battery must equal the total drop across each resistor • V t= V 1 + V 2 + V 3 • The total resistance in a series circuit is the sum of all the resistors. • Rt=R 1+R 2 +R 3

Electricity More on Parallel Circuits

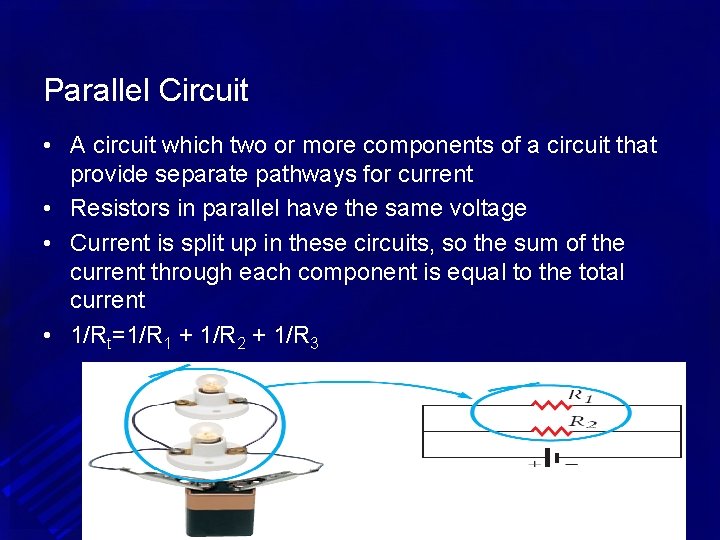
Parallel Circuit • A circuit which two or more components of a circuit that provide separate pathways for current • Resistors in parallel have the same voltage • Current is split up in these circuits, so the sum of the current through each component is equal to the total current • 1/Rt=1/R 1 + 1/R 2 + 1/R 3

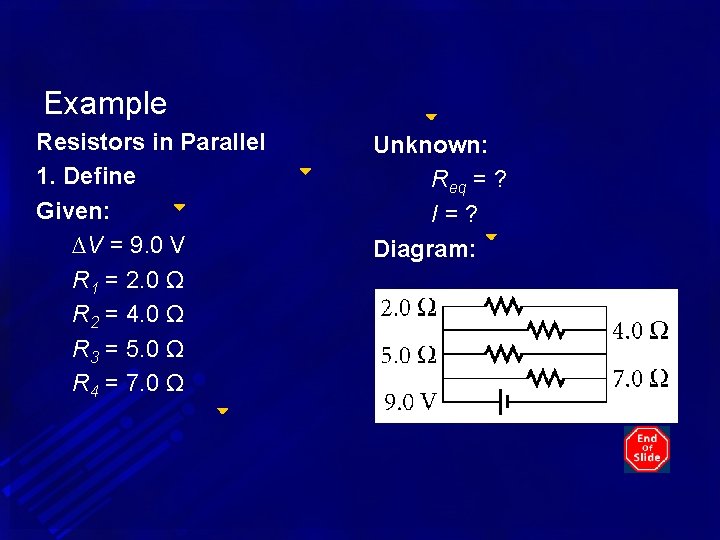
Example • A 9. 0 V battery is connected to four resistors, as shown at right. Find the equivalent resistance for the circuit and the total current in the circuit.

Example Resistors in Parallel 1. Define Given: ∆V = 9. 0 V R 1 = 2. 0 Ω R 2 = 4. 0 Ω R 3 = 5. 0 Ω R 4 = 7. 0 Ω Unknown: Req = ? I=? Diagram:

Kirchoff’s Laws/Ohm’s Law for Parallell Circuits