ELECTRICITY Electric Charge Two positive charges or two












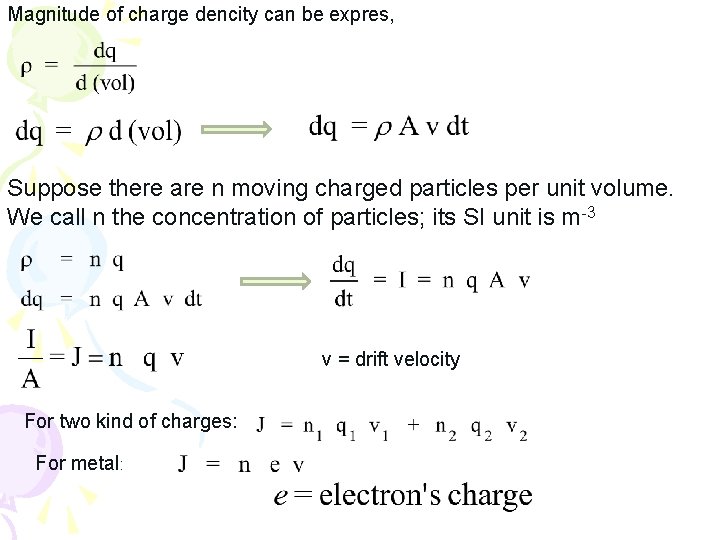








- Slides: 42

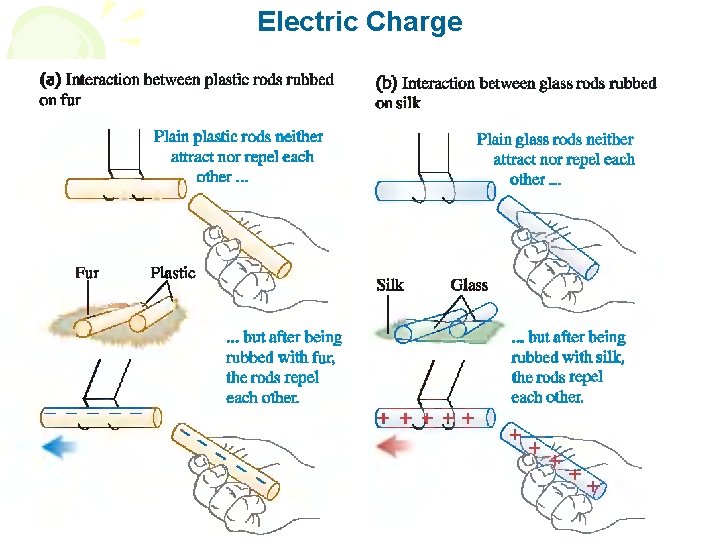
ELECTRICITY

Electric Charge

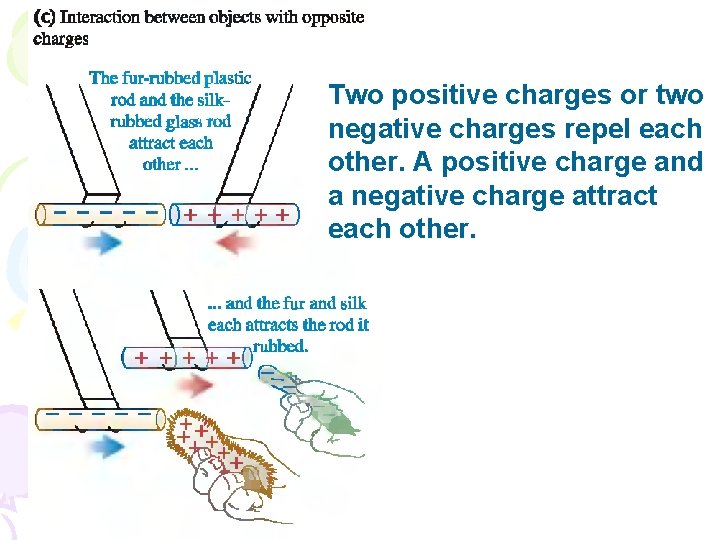
Two positive charges or two negative charges repel each other. A positive charge and a negative charge attract each other.

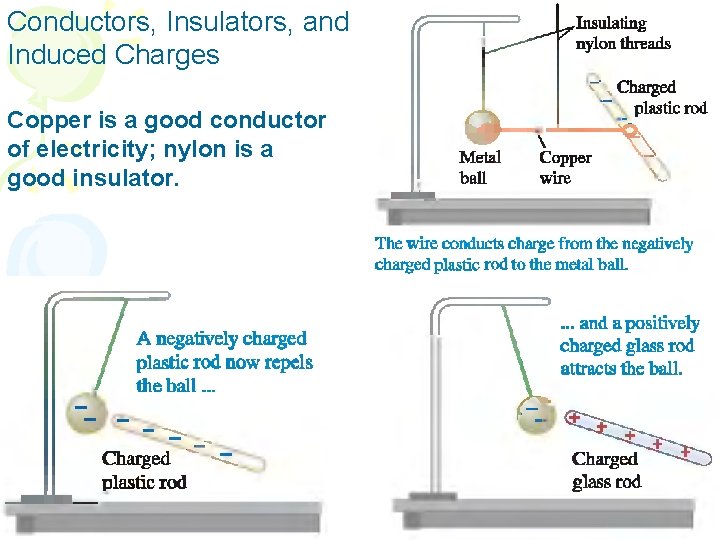
Conductors, Insulators, and Induced Charges Copper is a good conductor of electricity; nylon is a good insulator.

• Electrical conductors are materials in which electric charges move freely, whereas electrical insulators are materials in which electric charges cannot move freely. • Semiconductors are a third class of materials, and their electrical properties are somewhere between those of insulators and those of conductors. • Silicon and germanium are well-known examples of semiconductors commonly used in the fabrication of a variety of electronic devices, such as transistors and light-emitting diodes.

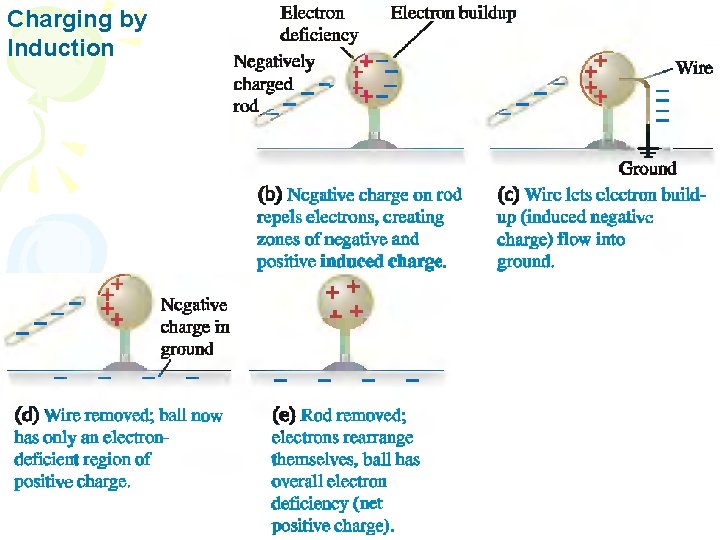
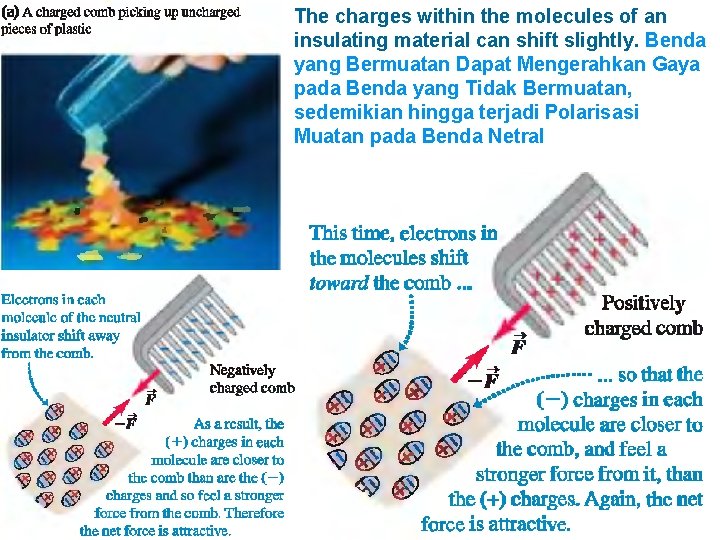
Charging by Induction

The charges within the molecules of an insulating material can shift slightly. Benda yang Bermuatan Dapat Mengerahkan Gaya pada Benda yang Tidak Bermuatan, sedemikian hingga terjadi Polarisasi Muatan pada Benda Netral

A. Coulomb’s Law 1. The Electric Force Between Two Point Charges • The magnitude of the electric force between two point charges is directly proportional to the product of the charges and inversely proportional to the square of the distance between them. = The proportionality constant y Q 1 Q 2 O 0 = Vacum permitivity = 8. 85 x 10 -12 C 2/Nm 2 x

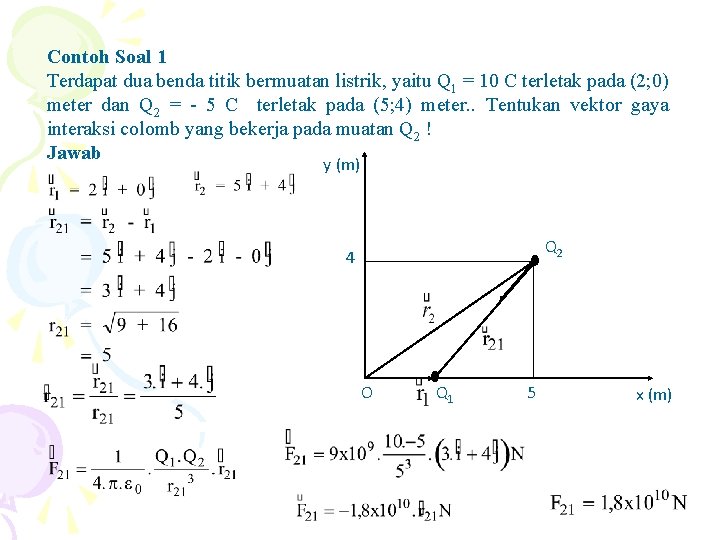
Contoh Soal 1 Terdapat dua benda titik bermuatan listrik, yaitu Q 1 = 10 C terletak pada (2; 0) meter dan Q 2 = - 5 C terletak pada (5; 4) meter. . Tentukan vektor gaya interaksi colomb yang bekerja pada muatan Q 2 ! Jawab y (m) Q 2 4 O Q 1 5 x (m)

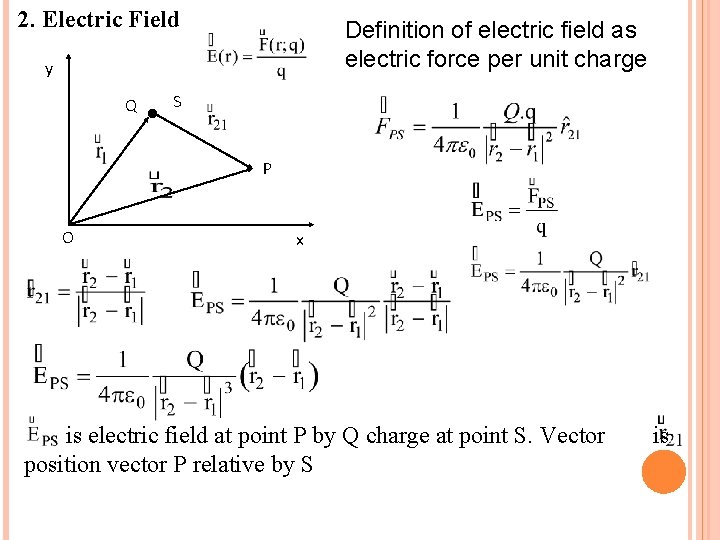
2. Electric Field Definition of electric field as electric force per unit charge y Q S P O x is electric field at point P by Q charge at point S. Vector position vector P relative by S is

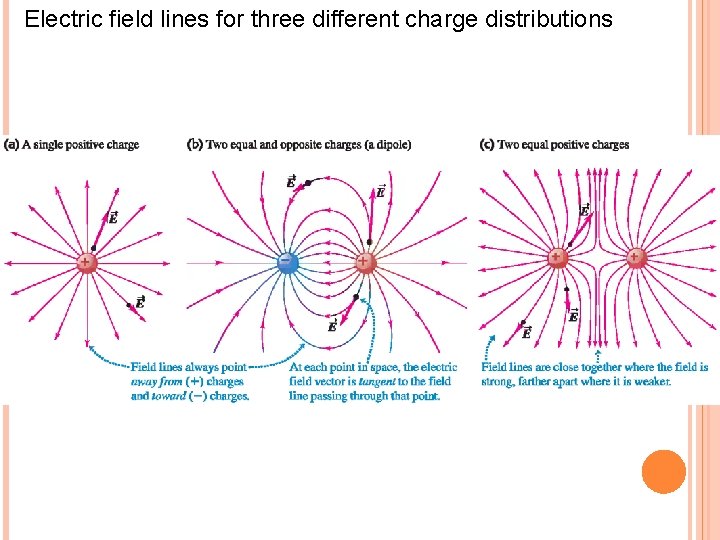
Electric field lines for three different charge distributions

Contoh soal 2 Suatu muatan sumber sebesar 2 C terletak pada posisi S(1; 4) meter. Hitunglah kuat medan listrik di titik P pada posisi (5; 1) meter ! JAWAB: y (m) S 4 P O 1 5 x (m) N. C-1

3. Electric Potential • Electric Potential at a point is potential energy per unit charge at that point. V is deference potential and is electric field (can defind by Coulomb Law), and V (r 0) be choice to ro = , because electrik potential at ro = , V ( ) = 0, so:

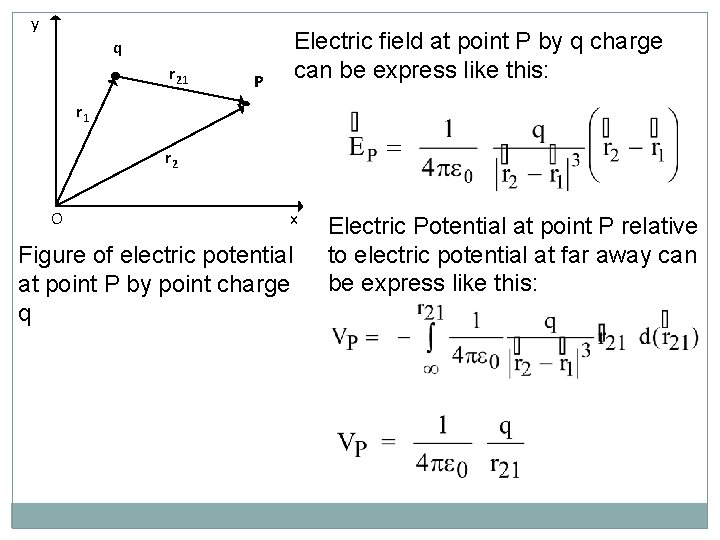
y Electric field at point P by q charge can be express like this: q r 21 P r 1 r 2 O x Figure of electric potential at point P by point charge q Electric Potential at point P relative to electric potential at far away can be express like this:

. Contoh Soal 3 Terdapat tiga muatan benda titik yang dipasang tetap di tempatnya seperti ditunjukkan dalam Gambar di bawah ini. - 4 q a +q a a Hitunglah besarnya energi potensial listrik total dari ketiga muatan tersebut, jika diketahui besar muatan titik + 2 q Jawab: Besarnya energi potensial listrik total dari susunan muatan-muatan titik tersebut merupakan jumlah energi potensial listrik masing-masing pasangan muatan titik tersebut.

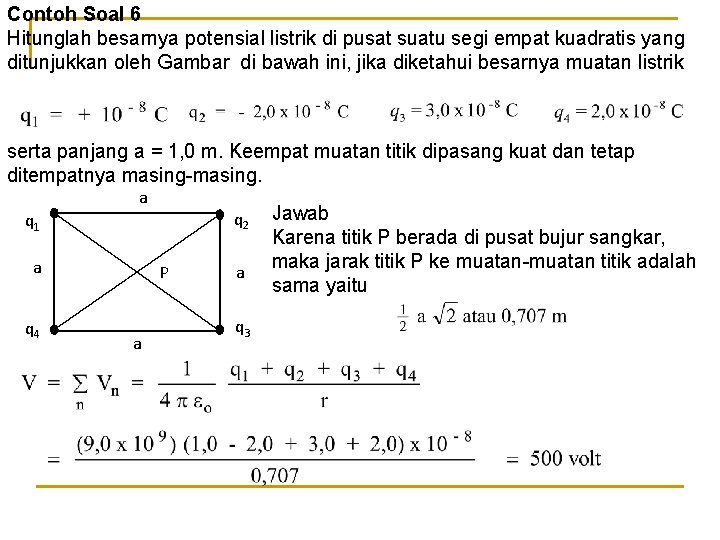
Contoh Soal 6 Hitunglah besarnya potensial listrik di pusat suatu segi empat kuadratis yang ditunjukkan oleh Gambar di bawah ini, jika diketahui besarnya muatan listrik serta panjang a = 1, 0 m. Keempat muatan titik dipasang kuat dan tetap ditempatnya masing-masing. a q 2 q 1 a q 4 P a a q 3 Jawab Karena titik P berada di pusat bujur sangkar, maka jarak titik P ke muatan-muatan titik adalah sama yaitu

B. Capacitor 1. Capacitance • Capacitor is capacitive system, mean can keep electric charge or electric field. Keeping of electric charge by a capacitor only temporary. That mean, electric charge at capacitor at any time can be discharged or cleared out. • Consider two conductors carrying charges of equal magnitude but of opposite sign. Such a combination of two conductors is called a capacitor. The conductors are called plates. • Electric charge + Q be keep at positive plate and Electric charge - Q be keep at negative plate.

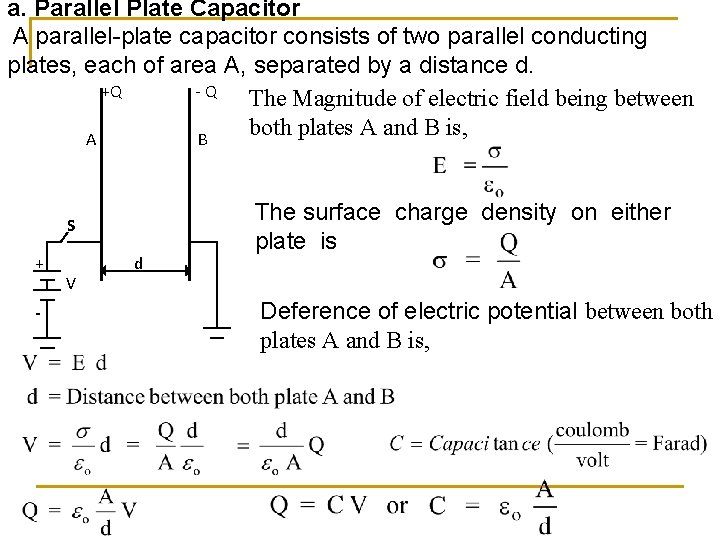
a. Parallel Plate Capacitor A parallel-plate capacitor consists of two parallel conducting plates, each of area A, separated by a distance d. +Q -Q The Magnitude of electric field being between both plates A and B is, A B S + - V d The surface charge density on either plate is Deference of electric potential between both plates A and B is,

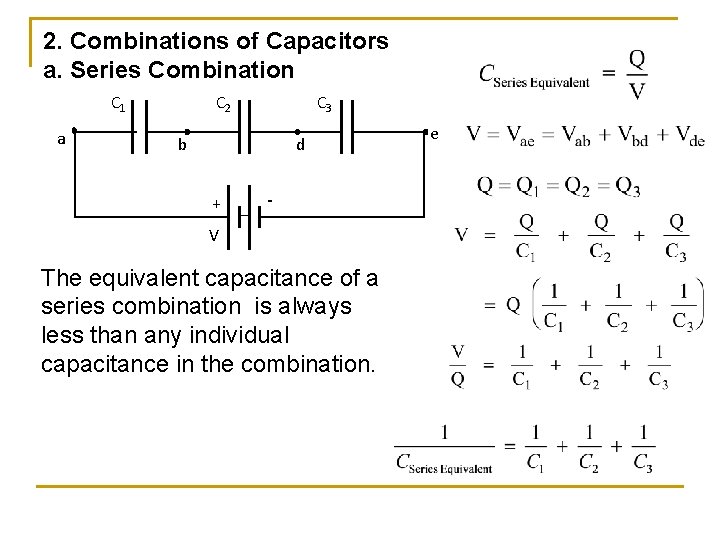
2. Combinations of Capacitors a. Series Combination C 1 a C 2 C 3 d b + - V The equivalent capacitance of a series combination is always less than any individual capacitance in the combination. e

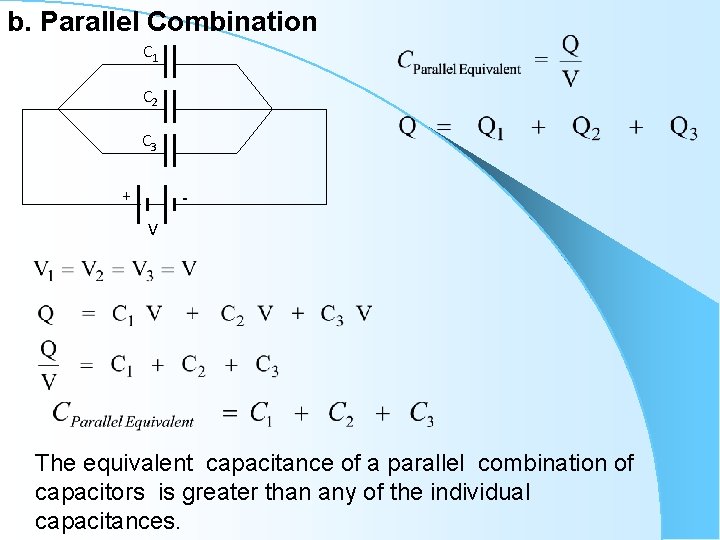
b. Parallel Combination C 1 C 2 C 3 + V The equivalent capacitance of a parallel combination of capacitors is greater than any of the individual capacitances.

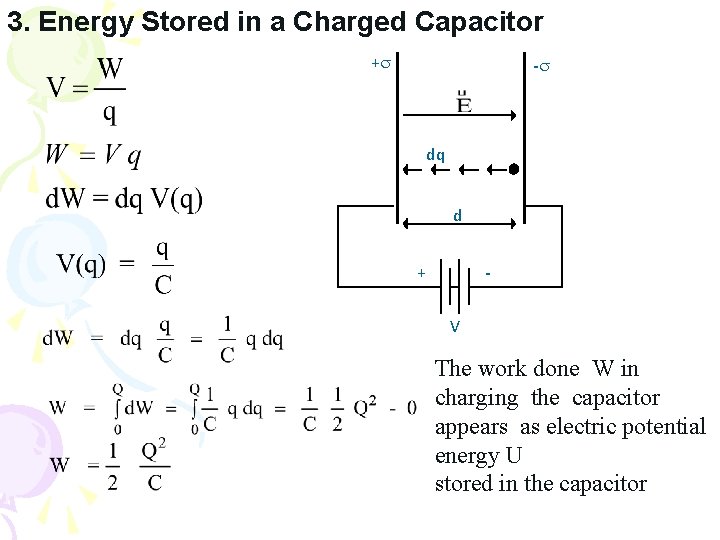
3. Energy Stored in a Charged Capacitor + - dq d + V The work done W in charging the capacitor appears as electric potential energy U stored in the capacitor

Thus, electric potential energy U stored in the capacitor is Because Q = C V, so For parallel plate capacitor with dielectrics, Electric potential energy stored in the capacitor per unit volume u

Contoh soal 7 Suatu kapasitor terbuat dari plat-plat sejajar yang berjarak serba sama satu sama lain sebesar 0, 1 cm. Jika kapasitor tersebut berisi udara, hitunglah luas plat-plat kapasitor itu agar supaya menghasilkan kapasitansi sebesar 2 farad ! Jawab Contoh soal 8 Suatu kapaitor plat sejajar berisi udara. Kedua plat tersebut berjarak serba sama sebesar 10 mm, dan luas penampangnya 100 cm 2. . Suatu bahan dielektrik yang konstantanya 7, disisipkan diantara kedua plat tersebut. Jika suatu sumber tegangan listrik sebesar 100 volt dipasang pada kapasitor sebelum disisipi dielektrik, kemudian sumber tersebut diputus, maka hitunglah (a). kapasitansi kapasitor sebelum bahan dielektrik disisipkan, (b). jumlah muatan bebas yang tersimpan. , (c). medan listrik di antara kedua plat, dan (d). medan listrik pada bahan dielektrik

Jawab a. Ketika dihubungkan dengan sumber tegangan listrik, kapasitor belum disisipi bahan dielektrik, sehingga kapasitansinya adalah : b. Jumlah muatan yang tersimpan dalam kapasitor adalah : Jumlah muatan listrik yang tersimpan ini sebelum bahan dielektrik disisipkan. Karena pemasangan bahan dielektrik dilakukan setelah pengisian yang dalam soal disebutkan adanya pemutusan hubungan dengan sumber tegangan, maka walaupun bahan dielektrik disisipkan tidak mempengaruhi jumlah muatan tersebut.

c. Medan listrik di antara dua plat adalah : Untuk menghitung medan listrik di antara kedua plat digunakan hukum Gauss. Dari hukum Gauss tersubut diperoleh persamaan : Begitu pula untuk medan listrik Eo ini tidak berubah walaupun disisipi bahan dielektrik, sebab penyisipan bahan dielektrik setelah pemutusan hubungan dengan sumber tegangan listrik. Nampak bahwa kuat medan listrik Eo sebanding dengan jumlah muatan q. Sehingga jika jumlah muatan q tidak berubah, maka besar kuat medan listrik Eo juga tidak berubah besarnya.

d. Medan listrik di dalam bahan dielektrik adalah

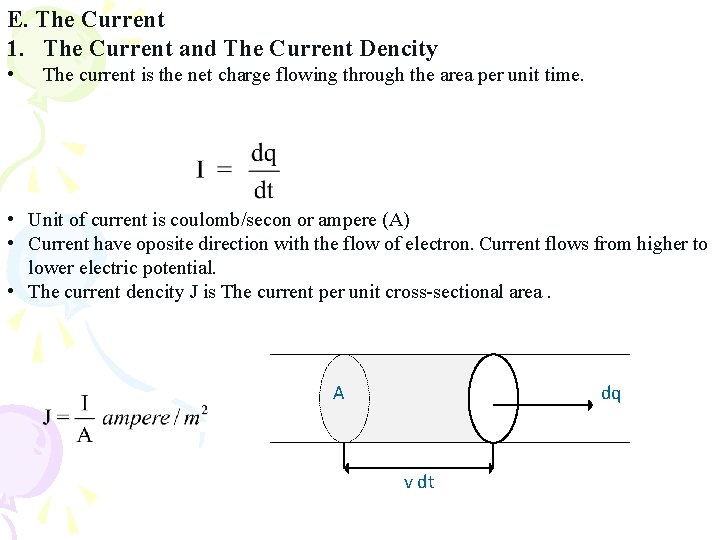
E. The Current 1. The Current and The Current Dencity • The current is the net charge flowing through the area per unit time. • Unit of current is coulomb/secon or ampere (A) • Current have oposite direction with the flow of electron. Current flows from higher to lower electric potential. • The current dencity J is The current per unit cross-sectional area. A dq v dt
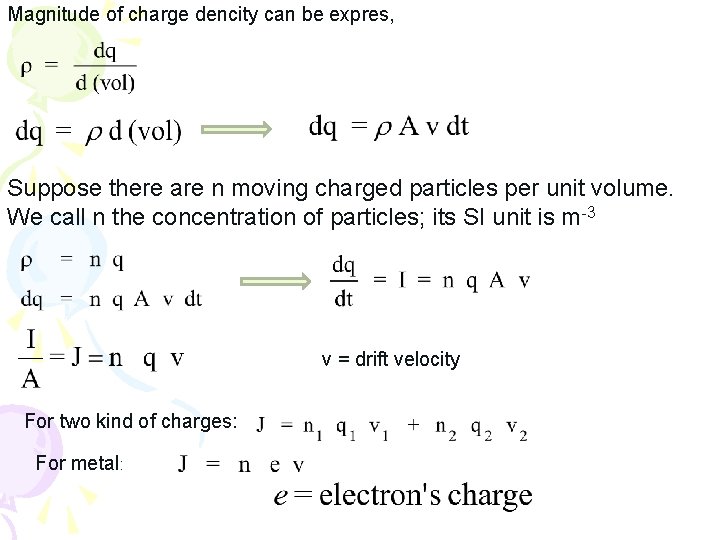
Magnitude of charge dencity can be expres, Suppose there are n moving charged particles per unit volume. We call n the concentration of particles; its SI unit is m-3 v = drift velocity For two kind of charges: For metal:

2. Ohm’s Law This figure below is A conductor with uniform cross section. The current density is uniform over any cross section, and the electric field is constant along the length. P I E Q A When Ohm's law is obeyed, p is constant and independent of the magnitude of `the electric field, so E is directly proportional to J. L R is resintance, A is the crosssectional area , L is lenght, is resistivity , dan is conductivity

3. Joule’s Law a b I • Section of conductor a-b has potential defference V, flowed current I. Potential Va higher than potential. Vb, so Va - Vb = V. • Because current I is constant, so drift velocity at a equal with at b. If carrier of charges dq flow under electric potential V, so that charges find energy increases d. U = V dq. • Because the current I is constant, V constant to, so there is not change kinetic energy, althought get energy increases d. U = V dq. That energy increases change became heat energy. That energy accepted metal with power: Because V = i. R, so :

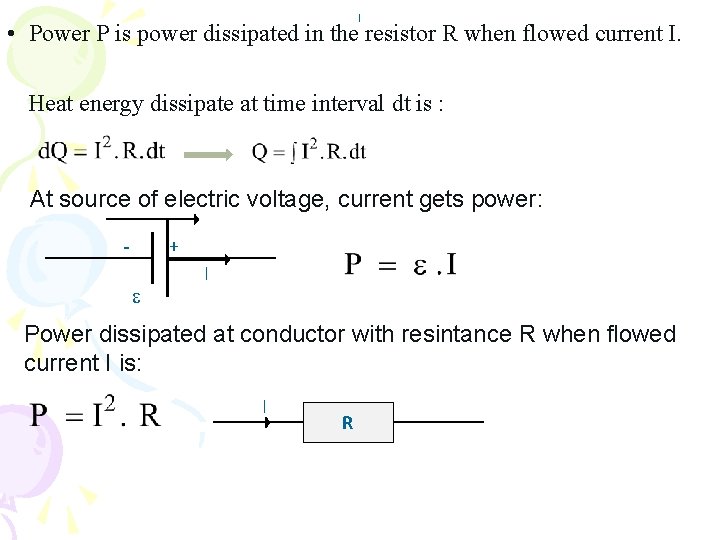
I • Power P is power dissipated in the resistor R when flowed current I. Heat energy dissipate at time interval dt is : At source of electric voltage, current gets power: + I Power dissipated at conductor with resintance R when flowed current I is: I R

4. Direct-Current Circuits a. Conservation Law of charges and Conservation Law of Energy in Simple Electric Circuit. ; r P + Q - I Vb Va a Energy conservation law : Power give to current equal with power was disappear. R b Quantity ( . I ) is power give to current, I 2. R is disappear power to external resistance R, whereas I 2. r is disappear power to internal resistance r. A potential gain of : is associated with the emf (electromotive force The potential Vab , called the terminal voltage.

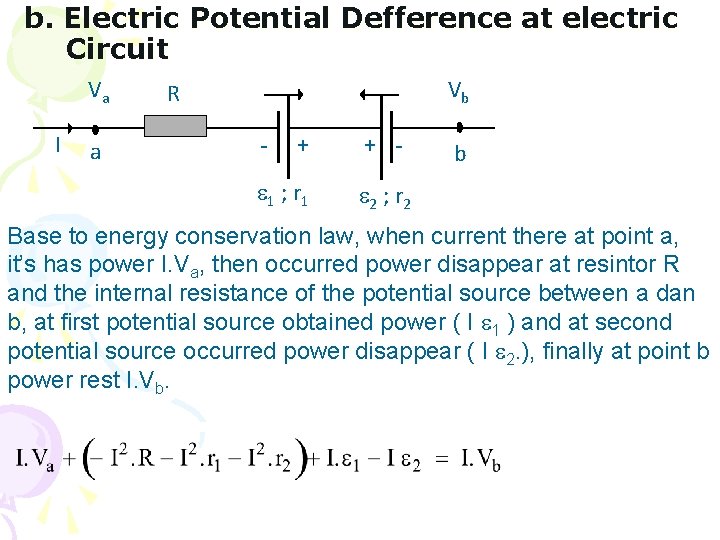
b. Electric Potential Defference at electric Circuit Va I a Vb R - + 1 ; r 1 + - b 2 ; r 2 Base to energy conservation law, when current there at point a, it’s has power I. Va, then occurred power disappear at resintor R and the internal resistance of the potential source between a dan b, at first potential source obtained power ( I 1 ) and at second potential source occurred power disappear ( I 2. ), finally at point b power rest I. Vb.

An agreement in this equation use is: a. Positif direction is from a to b. b. given positive sign and reverse given negative sign.

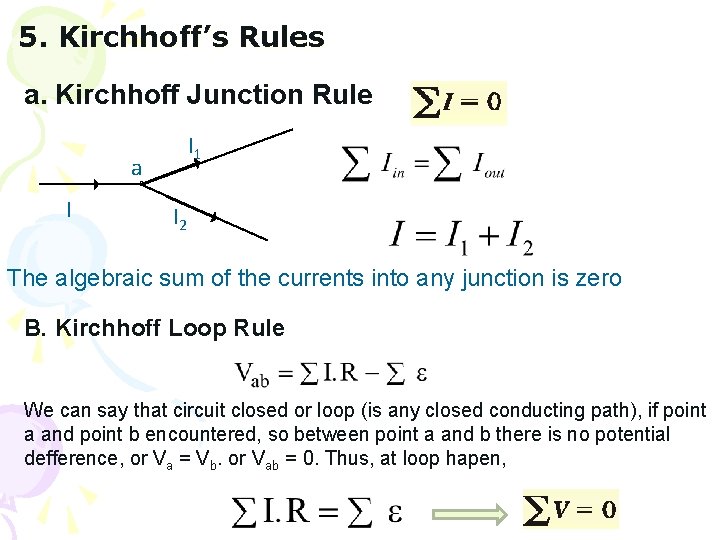
5. Kirchhoff’s Rules a. Kirchhoff Junction Rule I 1 a I I 2 The algebraic sum of the currents into any junction is zero B. Kirchhoff Loop Rule We can say that circuit closed or loop (is any closed conducting path), if point a and point b encountered, so between point a and b there is no potential defference, or Va = Vb. or Vab = 0. Thus, at loop hapen,

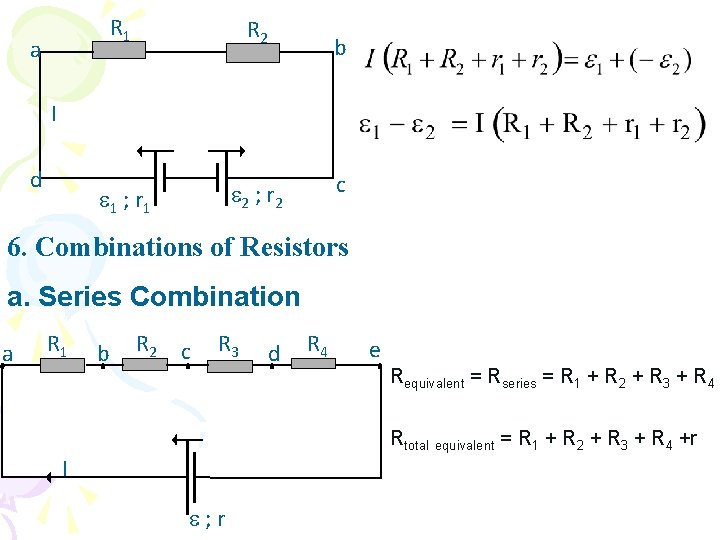
R 1 R 2 1 ; r 1 2 ; r 2 a b I d c 6. Combinations of Resistors a. Series Combination a R 1 b R 2 c R 3 d R 4 e Requivalent = Rseries = R 1 + R 2 + R 3 + R 4 Rtotal equivalent = R 1 + R 2 + R 3 + R 4 +r I ; r

With Kirchhoff. s Loop Rule we can define equation like this: • Component ( - I. r) called the terminal voltage, those magnitude equal with electric potential used by external resistors.

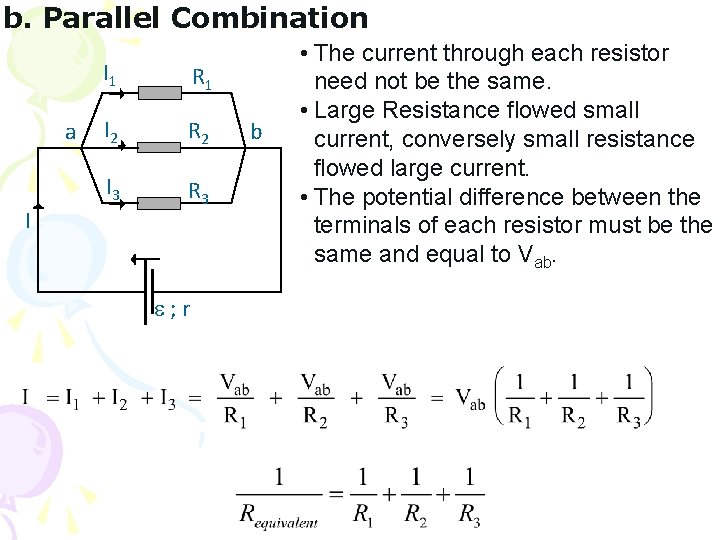
b. Parallel Combination a I I 1 R 1 I 2 R 2 I 3 R 3 ; r b • The current through each resistor need not be the same. • Large Resistance flowed small current, conversely small resistance flowed large current. • The potential difference between the terminals of each resistor must be the same and equal to Vab.

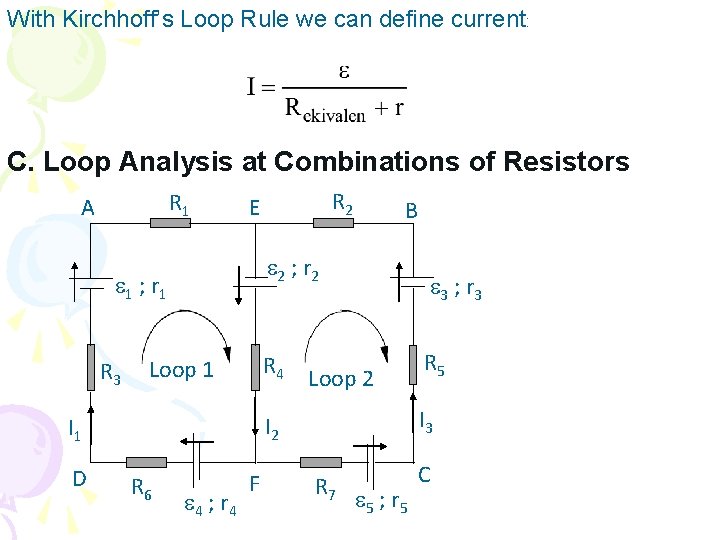
With Kirchhoff’s Loop Rule we can define current: C. Loop Analysis at Combinations of Resistors R 1 A R 4 Loop 1 3 ; r 3 Loop 2 R 6 4 ; r 4 F R 5 I 3 I 2 I 1 D B 2 ; r 2 1 ; r 1 R 3 R 2 E R 7 5 ; r 5 C

Loop I : Loop II : Contoh soal 9 Jika dalam rangkaian Gambar di atas diketahui R 1 = R 2 = R 3 = R 5 = 10 , R 6= R 7 = 20 , R 4 = 15 , r 1 = r 2 = r 3 = r 4 = r 5 = 1 , 1 = 6 V, 2 = 4 = 12 V, 3 = 20 V, dan 5 = 30 V. Hitunglah kuat arus listrik yang mengalir dalam rangkaian tersebut !

Loop I : 6 + 12 = I 1 ( 10 + 20 + 1 ) + I 2 ( 15 + 1 ) 30 = I 1 (42) + I 2 (16) (I) Loop II : - 12 - 20 - 12 = - I 3 (10 + 20 + 1) - I 2 (15 + 1) - 44 = - I 3 (42) - I 2 (16) Dari persamaan (I) dan (III) diperoleh : 30 = (I 2 - I 3) (42) + I 2 (16) atau 30 = I 2 (58) - I 3 (42) Dari persamaan (II), (III), dan (IV) diperoleh : I 2 = 1 A , I 3 = 0, 67 A, dan I 1 = 0, 33 A (II) (IV)
