Electricity and Magnetism I Griffiths Chapter 3 Laplaces










![V(x, y) = C Exp[-npx/a] Sin[npy/a] satisfies Laplace’s equation and 75% of the boundary V(x, y) = C Exp[-npx/a] Sin[npy/a] satisfies Laplace’s equation and 75% of the boundary](https://slidetodoc.com/presentation_image_h/b1c6a929ad8605b4f0eba099fe0d981b/image-16.jpg)
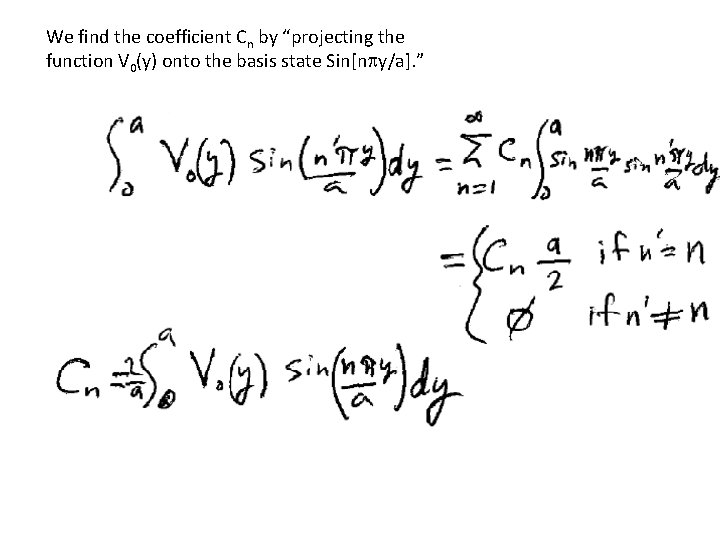










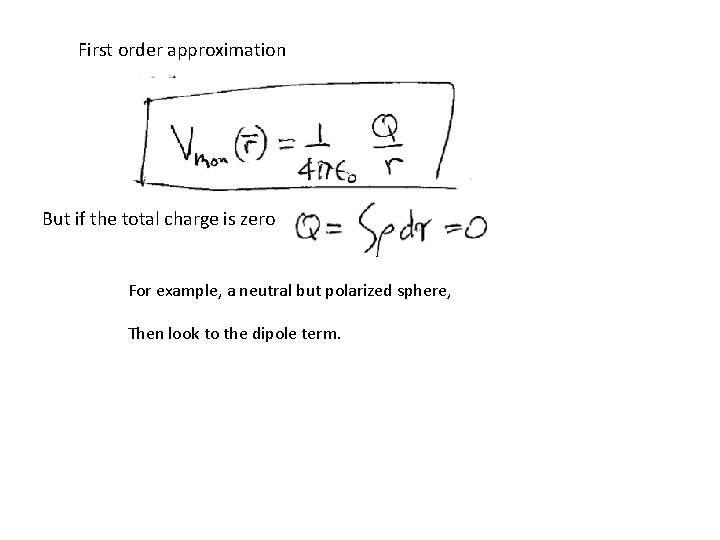










- Slides: 45

Electricity and Magnetism I Griffiths Chapter 3

Laplace’s Equation in 3 D implies that the potential at a given point V(x, y, z) has no minima or maxima in vacuum where it satisfies Laplace’s equation. Extrema occur only at boundaries (surfaces of conductors), where there are charges.

First uniqueness theorem The solution V(x, y, z) to Laplaces Equation is unique in a volume v if V is specified on the surface S that bounds v. This is your license to guess the solution If you guess a solution that satisfies Laplace’s equation, AND which satisfies the boundary conditions, that’s it. There is no other solution.

What is Laplace’s equation in one dimension? What is its solution V(x)? How many boundary conditions do we need to uniquely specify the solution? Can one of the boundaries be infinity?

Second uniqueness theorem The electric field E(r) is uniquely determined in a volume v bounded by conductors if boundary surface charge densities s, and a charge density r(r) in v, are specified. conductors Holds also if there is no outer conductor and the boundary is at infinity (where s = 0).

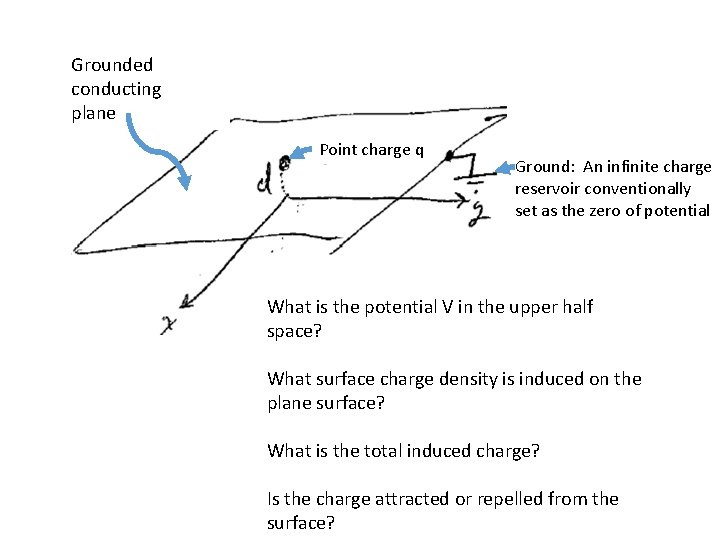
Grounded conducting plane Point charge q Ground: An infinite charge reservoir conventionally set as the zero of potential What is the potential V in the upper half space? What surface charge density is induced on the plane surface? What is the total induced charge? Is the charge attracted or repelled from the surface?

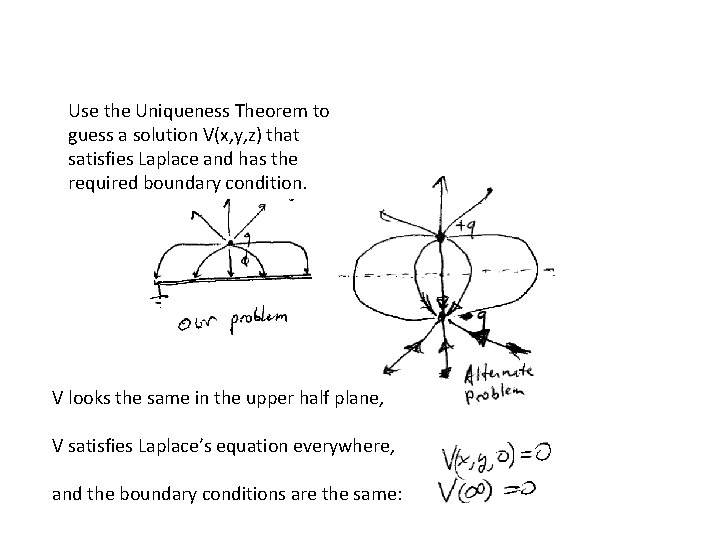
Use the Uniqueness Theorem to guess a solution V(x, y, z) that satisfies Laplace and has the required boundary condition. V looks the same in the upper half plane, V satisfies Laplace’s equation everywhere, and the boundary conditions are the same:

The two charge problem is easy to solve by superposition As it should on the grounded plane As it should for potentials of point charges So the potential V(x, y, z) is found for the upper half space. In the lower half space, V= 0. The problem looks like a mirror: This trick is called “method of images. ” The fictitious charge is called the “image charge”.

What is the induced surface charge density? The normal derivative of V evaluated at the surface Actual induced surface charge density is negative, just like the fictitious image charge. The maximum s occurs directly under q. Force on q is attractive. Total actual induced charge is Same as image charge

The energy of charge and image charge would be But the energy of charges in the grounded conductor at zero potential is zero, so the actual energy is half. (Field energy actually exists only in the upper half space.

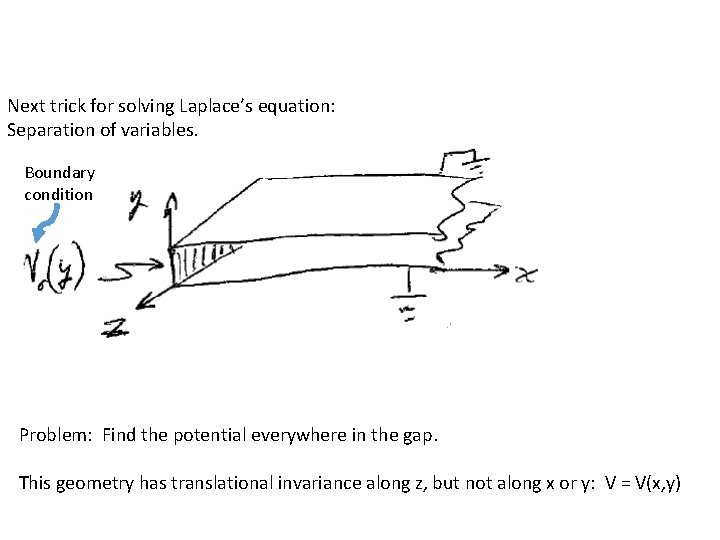
Next trick for solving Laplace’s equation: Separation of variables. Boundary condition Problem: Find the potential everywhere in the gap. This geometry has translational invariance along z, but not along x or y: V = V(x, y)

If V = V(x, y), Laplace’s equation has only two terms Trial solution: V(x, y, ) = X(x) Y(y) Can this satisfy the boundary conditions?

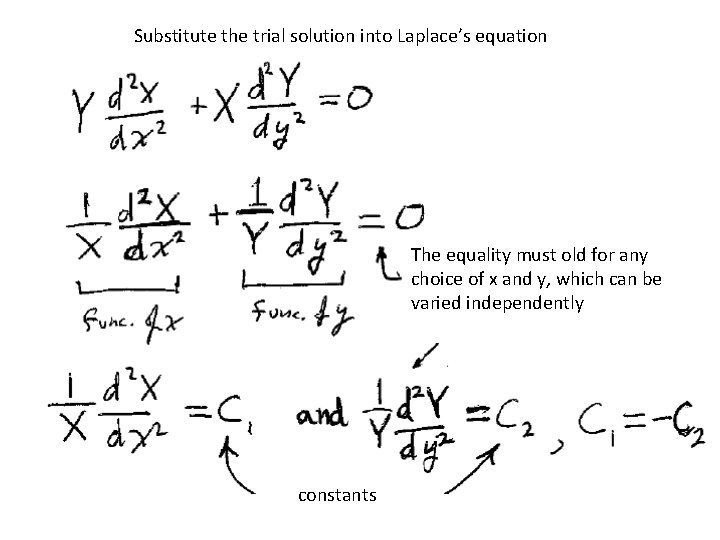
Substitute the trial solution into Laplace’s equation The equality must old for any choice of x and y, which can be varied independently constants

Each second order differential equation has two independent solutions with undetermined coefficients The potential V = X*Y

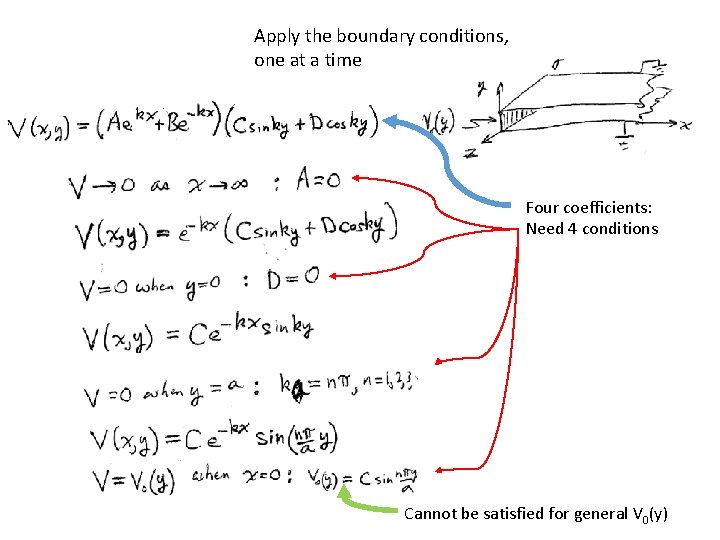
Apply the boundary conditions, one at a time Four coefficients: Need 4 conditions Cannot be satisfied for general V 0(y)
![Vx y C Expnpxa Sinnpya satisfies Laplaces equation and 75 of the boundary V(x, y) = C Exp[-npx/a] Sin[npy/a] satisfies Laplace’s equation and 75% of the boundary](https://slidetodoc.com/presentation_image_h/b1c6a929ad8605b4f0eba099fe0d981b/image-16.jpg)
V(x, y) = C Exp[-npx/a] Sin[npy/a] satisfies Laplace’s equation and 75% of the boundary conditions. It actually represents a set of solutions for different values of n. Any linear combination is also a solution. The most general solution would be This enables us to satisfy the final boundary condition, because is a Fourier series. We can always find a set of coefficients {Cn} such that the boundary condition can be satisfied.
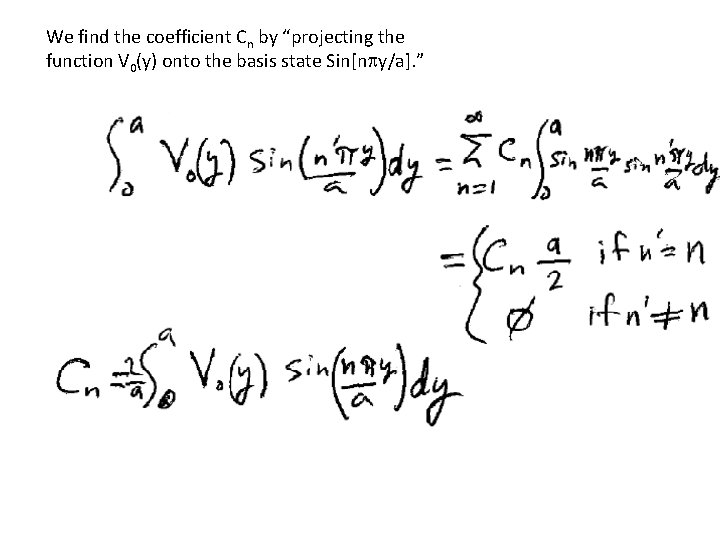
We find the coefficient Cn by “projecting the function V 0(y) onto the basis state Sin[npy/a]. ”

Example = constant

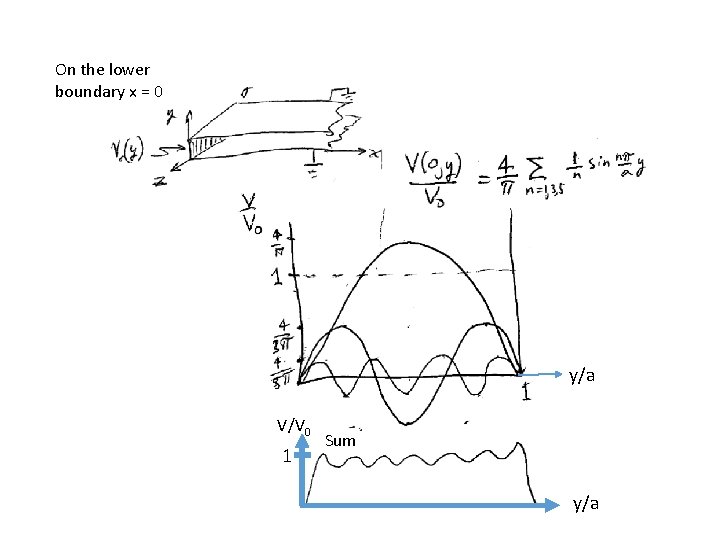
On the lower boundary x = 0 y/a V/V 0 1 Sum y/a

Separation of variables for Laplace’s equation in spherical coordinates Assume the problem has azimuthal symmetry Why is this assumption so often applicable to physics?

Separation of variables in spherical coordinates is a trick you will use again in quantum mechanics. For what problem? What quantum systems have spherical symmetry? What second order partial differential equation do you have to solve there?

With azimuthal symmetry, Laplace’s equation reduces to a two dimensional partial differential equation Trial solution (guess) Function only of r Function only of q Since r and q can be varied independently, each term must separately equal a constant, and the two constants must be opposite of each other.

Radial equation Polar angle equation * Special function: “Legendre polynomial”, an lth order polynomial in powers of Cosq The general solution is Coefficients to be determined by boundary conditions

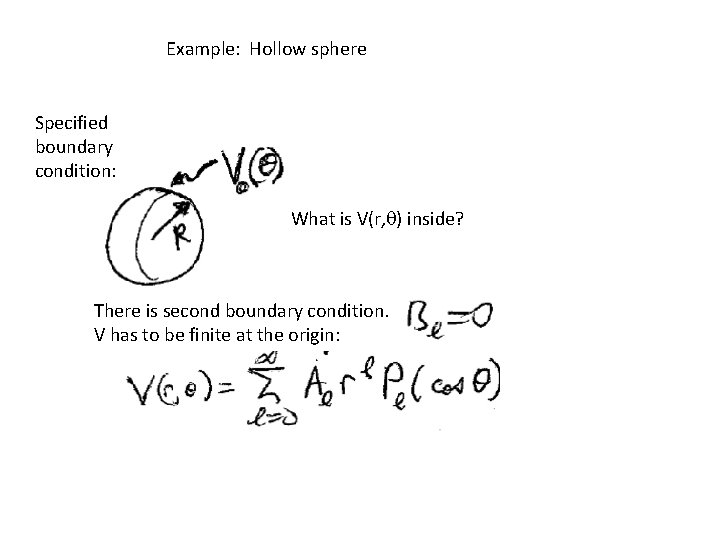
Example: Hollow sphere Specified boundary condition: What is V(r, q) inside? There is second boundary condition. V has to be finite at the origin:

To find coefficients, set V(R, q) = V 0(q) The equality can always be satisfied for any boundary condition because the {Pl(cosq)} span the space of functions of q defined on the interval {0, p}. The Pl are orthogonal.

Multiply both sides of boundary condition equation by the same function, integrate, and use orthogonality dq Act with Kronecker delta, then drop the primes. Put in Problem Solved! (By what property? )

Often the boundary condition V 0(q) will be some polynomial in sinq and/or cosq. This can be written as linear combinations of the Pl(cosq). Then you can use the orthogonality relations. This is related to the Wigner-Eckert Theorem in Quantum Mechanics. What is the Wigner-Eckert Theorem?

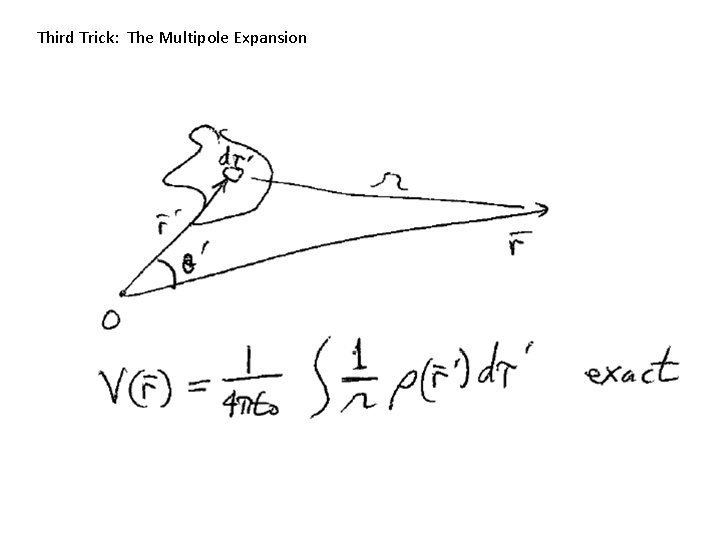
Third Trick: The Multipole Expansion

Obtain a simpler formula by expanding V in powers of 1/r.

Exact Multipole expansion (still exact) As soon as we truncate the series, it becomes an approximation, useful at large distances.
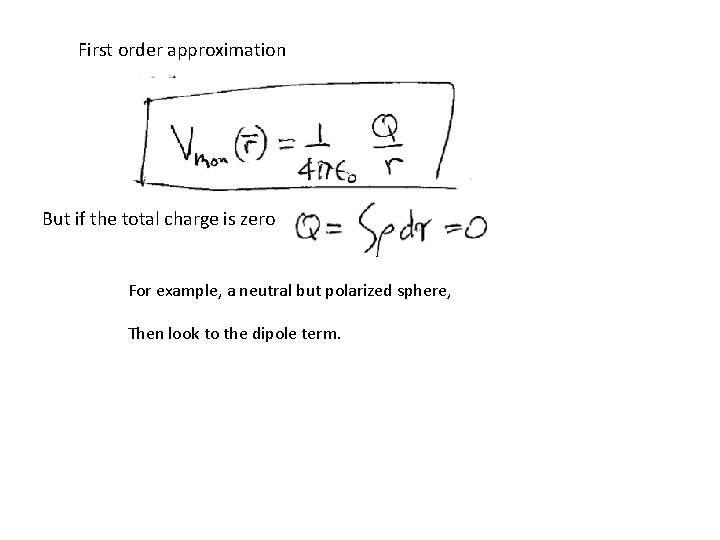
First order approximation But if the total charge is zero For example, a neutral but polarized sphere, Then look to the dipole term.

This integral is a function only of the distribution of charge: “dipole moment”

For point charges, the dipole moment is the sum of each charge times its position vector

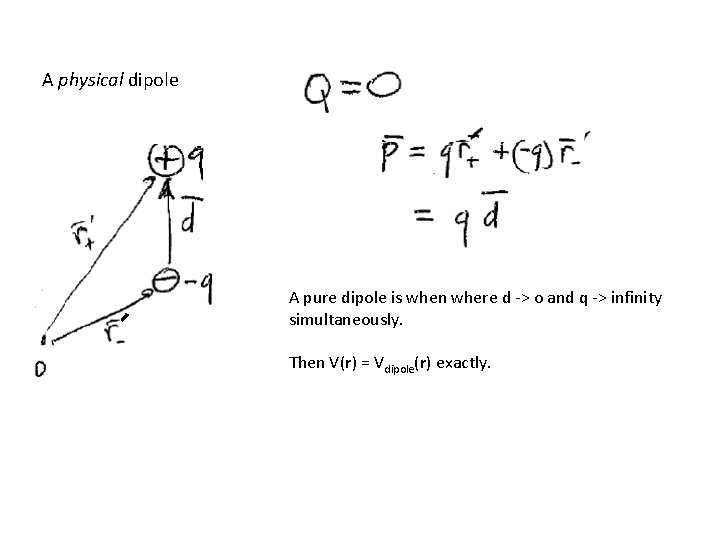
A physical dipole A pure dipole is when where d -> o and q -> infinity simultaneously. Then V(r) = Vdipole(r) exactly.

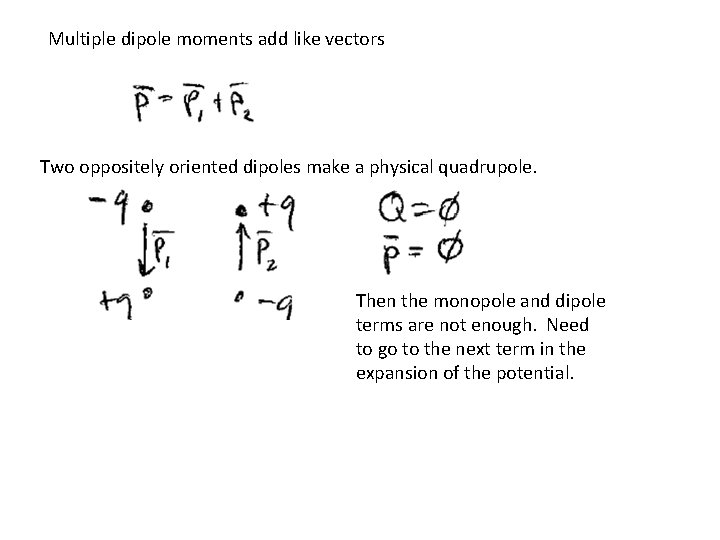
Multiple dipole moments add like vectors Two oppositely oriented dipoles make a physical quadrupole. Then the monopole and dipole terms are not enough. Need to go to the next term in the expansion of the potential.

Given a positive and negative charge, does the dipole moment vector point from positive to negative or from negative to positive? + or ? -

Put the origin at the negative charge. ez P = +q z ez+ -q 0 = +q z ez z + p - In physics, the direction of the dipole moment vector is from negative to positive. There are other conventions: “It is customary to represent dipole moment by a vector drawn from the positive to the negative charge” in molecules. Linus Pauling, General Chemistry (Dover, NY, 1970). In chemistry, the arrow gives the direction of electron displacement. Why does this discrepancy between physics and chemistry not matter?

The multipole expansion depends on where you put the origin. The monopole moment does not depend on the position of origin, because it is just the total charge.

The dipole moment generally does depend on the position of the origin

Which molecules have a dipole moment? H 2 O N 2 CO CO 2 Ar

Chemistry: Water molecules have a dipole moment of 1. 85 Debye. (Debye = 3. 336 x 10 -30 C-m) Water molecules in air are always zooming around with respect to whatever origin you choose, and How can chemists say that the dipole moment of H 2 O has a fixed value of 1. 85 D?

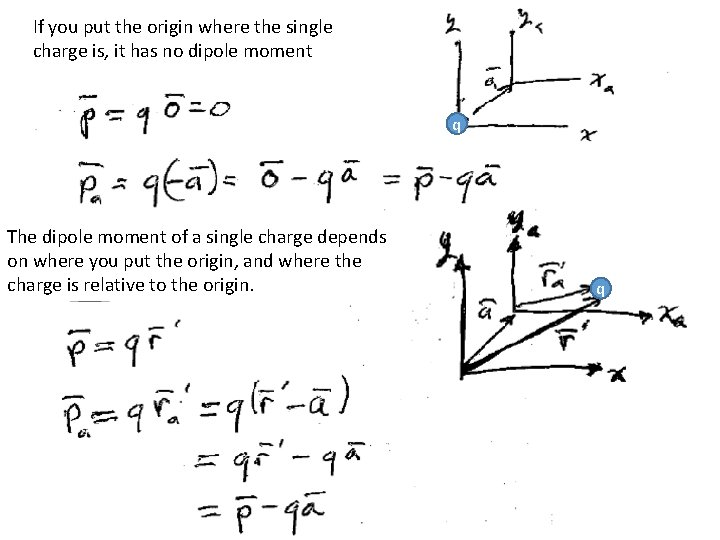
Can a single charge have a dipole moment?

If you put the origin where the single charge is, it has no dipole moment q The dipole moment of a single charge depends on where you put the origin, and where the charge is relative to the origin. q

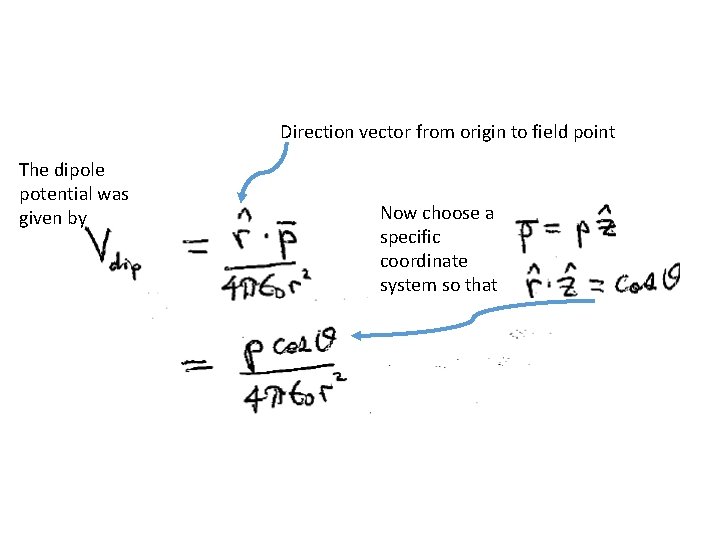
Direction vector from origin to field point The dipole potential was given by Now choose a specific coordinate system so that

The dipole filed is given by Take field points at different positions to see if the picture makes sense.