Electrical Circuits This presentation will Discuss the basic

Electrical Circuits This presentation will Discuss the basic laws in electric circuits Topics discussed are: Objectives: • • Ohm’s Law Circuit configuration Series, parallel circuits Definitions of Nodes and branches Kirchhoff’s laws statements Procedure to solve series circuits for Resistance, current and voltage Procedure to solve parallel circuits for Resistance, current and voltage This work is licensed under a Creative Commons Attribution 4. 0 International License. PPT submitted by RC 1353_810, RVR&JCCE, Guntur Creative Commons Attribution-Share. Alike 4. 0 International License. You are free to use, distribute and modify it, including for commercial purposes, provided you acknowledge the source and share-alike. 1

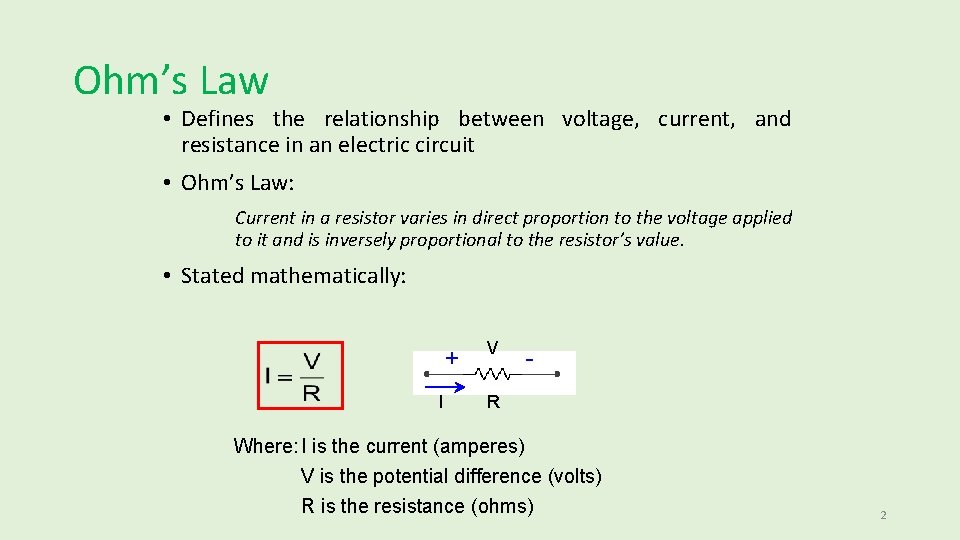
Ohm’s Law • Defines the relationship between voltage, current, and resistance in an electric circuit • Ohm’s Law: Current in a resistor varies in direct proportion to the voltage applied to it and is inversely proportional to the resistor’s value. • Stated mathematically: + I V - R Where: I is the current (amperes) V is the potential difference (volts) R is the resistance (ohms) 2

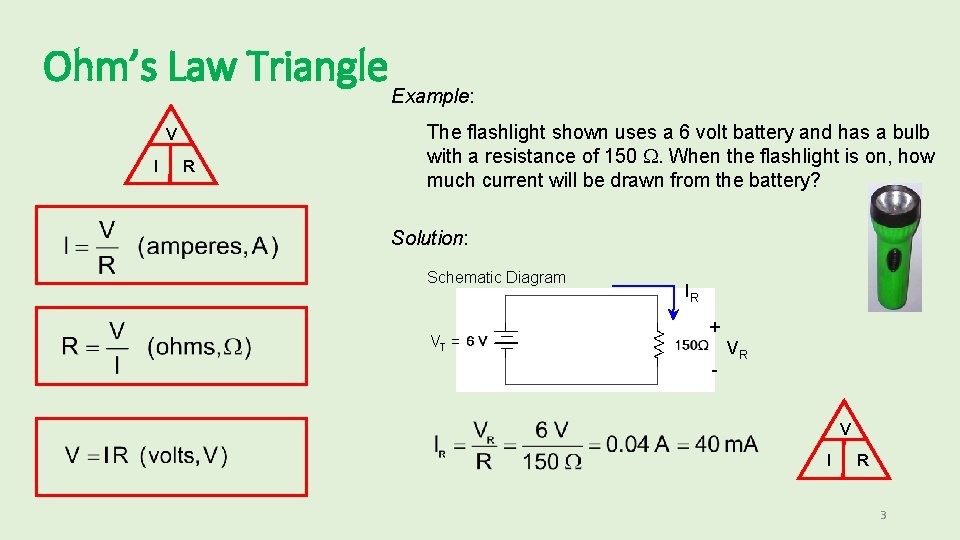
Ohm’s Law Triangle V I R Example: The flashlight shown uses a 6 volt battery and has a bulb with a resistance of 150 . When the flashlight is on, how much current will be drawn from the battery? Solution: Schematic Diagram VT = IR + - VR V I R 3

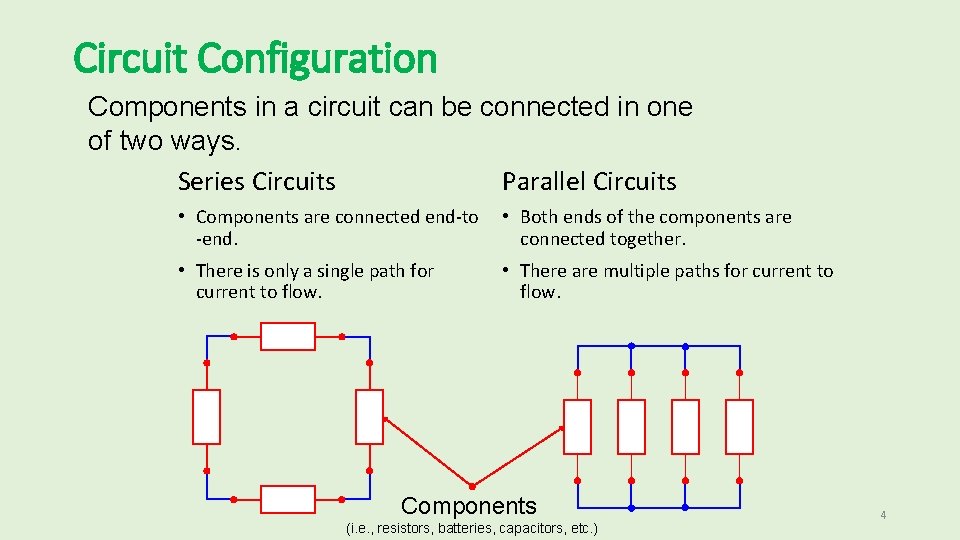
Circuit Configuration Components in a circuit can be connected in one of two ways. Parallel Circuits Series Circuits • Components are connected end-to -end. • Both ends of the components are connected together. • There is only a single path for current to flow. • There are multiple paths for current to flow. Components (i. e. , resistors, batteries, capacitors, etc. ) 4

Series Circuits Characteristics of a series circuit The current flowing through every series component is equal. The total resistance (RT) is equal to the sum of all of the resistances (i. e. , R 1 + R 2 + R 3). The sum of all of the voltage drops (VR 1 + VR 2) is equal to the total applied voltage (VT). This is called Kirchhoff’s Voltage Law. 5

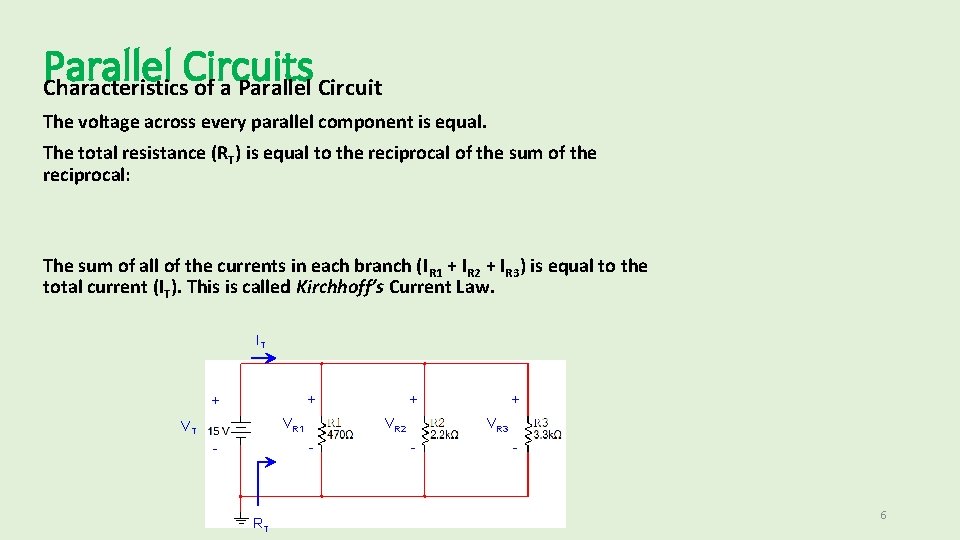
Parallel Circuits Characteristics of a Parallel Circuit The voltage across every parallel component is equal. The total resistance (RT) is equal to the reciprocal of the sum of the reciprocal: The sum of all of the currents in each branch (IR 1 + IR 2 + IR 3) is equal to the total current (IT). This is called Kirchhoff’s Current Law. IT + + VR 1 VT VR 2 - - RT + + VR 3 - - 6

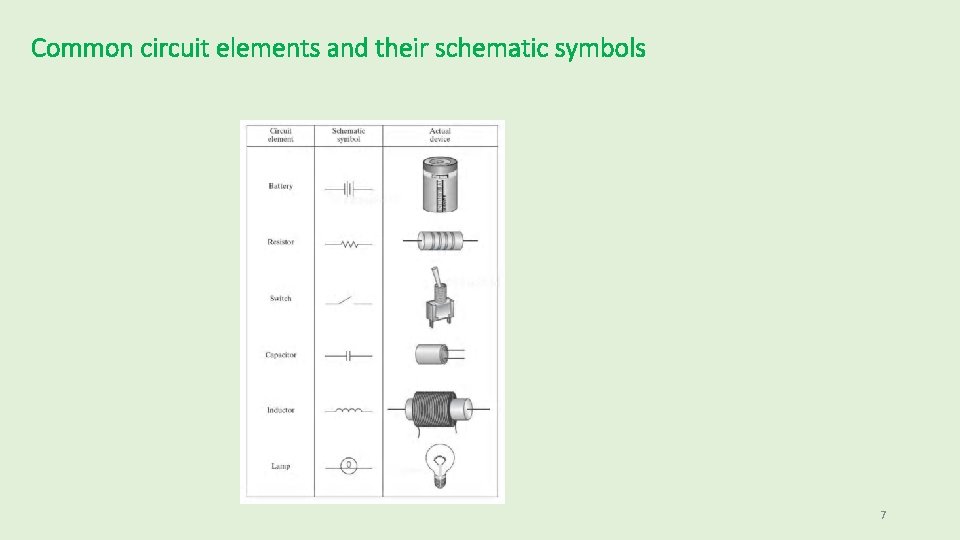
Common circuit elements and their schematic symbols 7

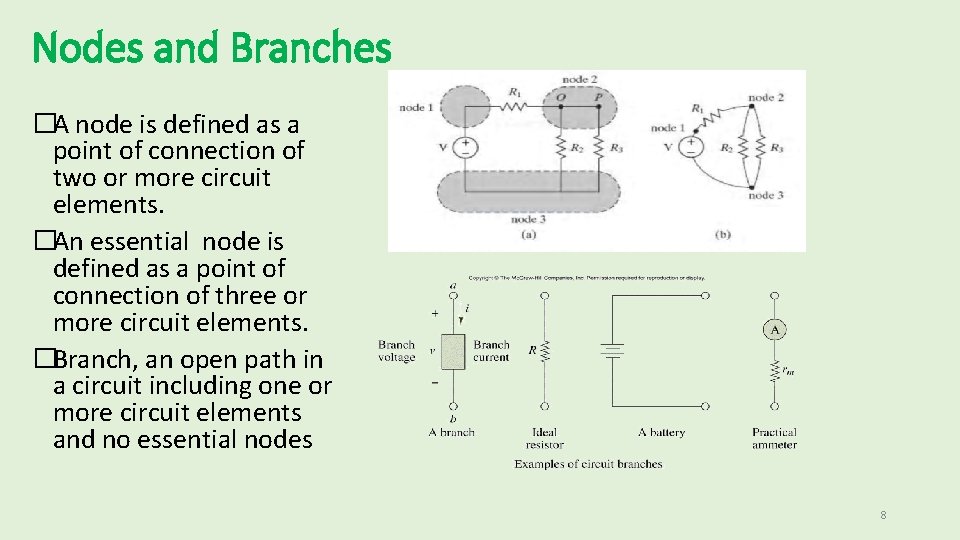
Nodes and Branches �A node is defined as a point of connection of two or more circuit elements. �An essential node is defined as a point of connection of three or more circuit elements. �Branch, an open path in a circuit including one or more circuit elements and no essential nodes 8

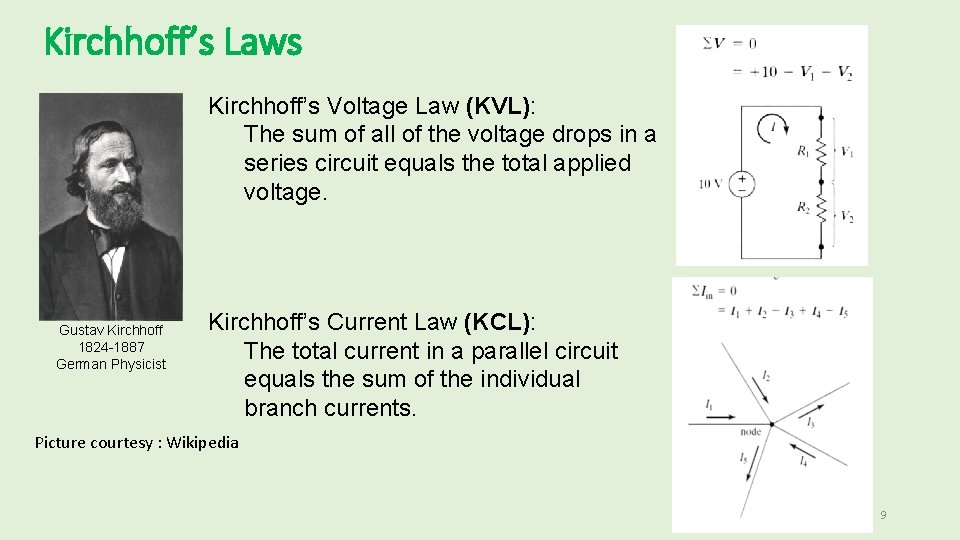
Kirchhoff’s Laws Kirchhoff’s Voltage Law (KVL): The sum of all of the voltage drops in a series circuit equals the total applied voltage. Gustav Kirchhoff 1824 -1887 German Physicist Kirchhoff’s Current Law (KCL): The total current in a parallel circuit equals the sum of the individual branch currents. Picture courtesy : Wikipedia 9

Series Circuits Characteristics of a series circuit • The current flowing through every series component is equal. • The total resistance (RT) is equal to the sum of all of the resistances (i. e. , R 1 + R 2 + R 3). • The sum of all of the voltage drops (VR 1 + VR 2) is equal to the total applied voltage (VT). This is called Kirchhoff’s Voltage Law. IT + VR 1 - + + VR 2 VT - - RT - + VR 3 10

Example: Series Circuit Example: For the series circuit shown, use the laws of circuit theory to calculate the following: • The total resistance (RT) • The current flowing through each component (IT, IR 1, IR 2, & IR 3) • The voltage across each component (VT, VR 1, VR 2, & VR 3) • Use the results to verify Kirchhoff’s Voltage Law. IT + VR 1 - IR 1 + + VT IR 2 - IR 3 RT - + VR 3 VR 2 - 11

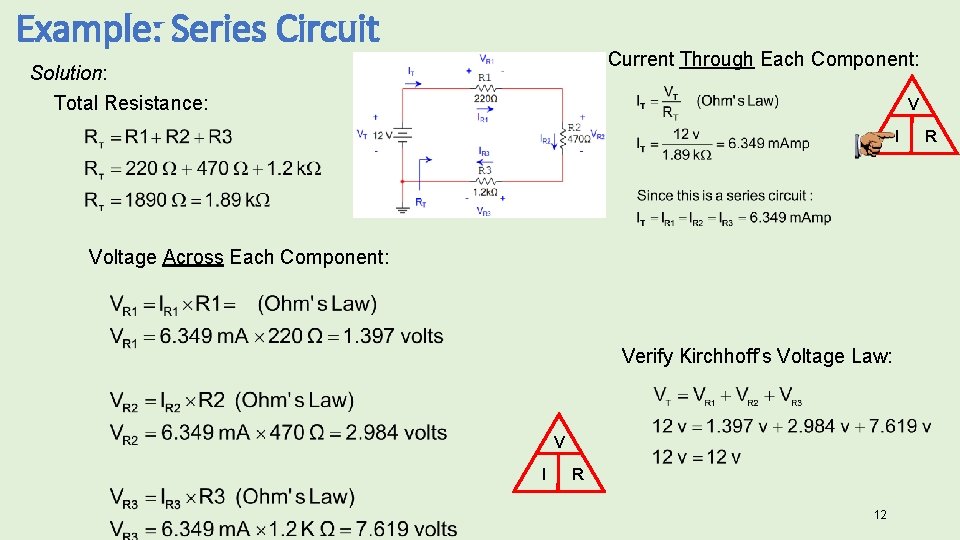
Example: Series Circuit Current Through Each Component: Solution: Total Resistance: V I Voltage Across Each Component: Verify Kirchhoff’s Voltage Law: V I R 12 R

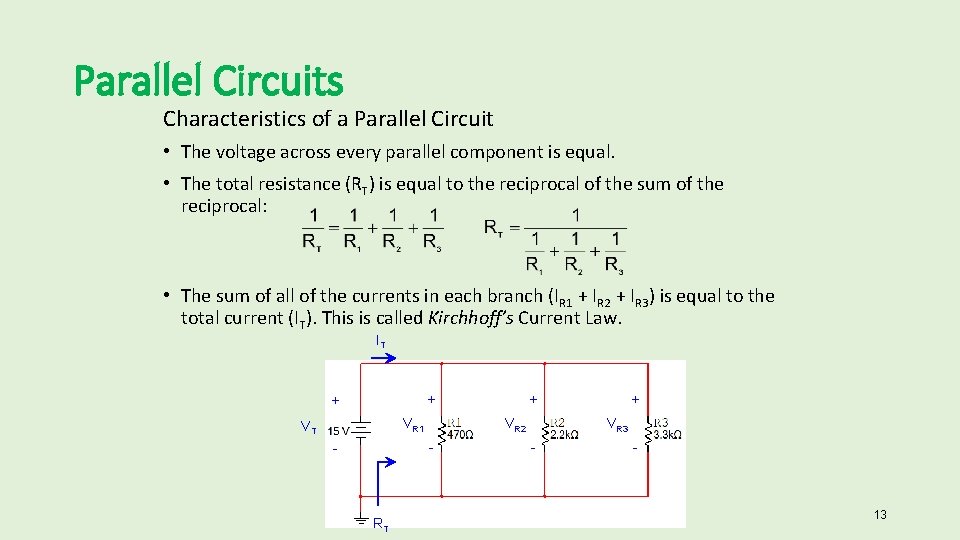
Parallel Circuits Characteristics of a Parallel Circuit • The voltage across every parallel component is equal. • The total resistance (RT) is equal to the reciprocal of the sum of the reciprocal: • The sum of all of the currents in each branch (IR 1 + IR 2 + IR 3) is equal to the total current (IT). This is called Kirchhoff’s Current Law. IT + + VR 1 VT VR 2 - - RT + + VR 3 - - 13

Example: Parallel Circuit Example: For the parallel circuit shown, use the laws of circuit theory to calculate the following: • The total resistance (RT) • The voltage across each component (VT, VR 1, VR 2, & VR 3) • The current flowing through each component (IT, IR 1, IR 2, & IR 3) • Use the results to verify Kirchhoff’s Current Law. IT IR 1 IR 2 + + VR 1 VT + VR 2 - - IR 3 + VR 3 - - 14 RT 14

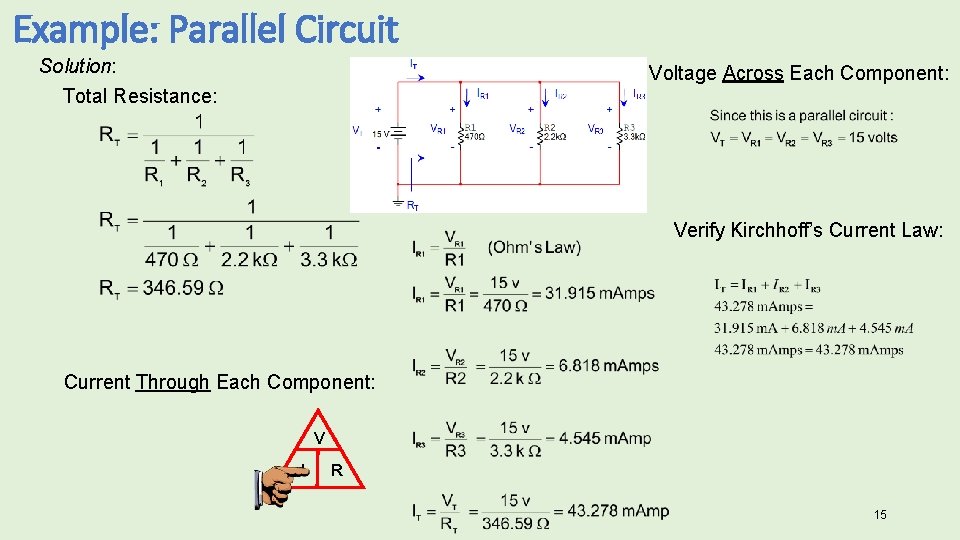
Example: Parallel Circuit Solution: Voltage Across Each Component: Total Resistance: Verify Kirchhoff’s Current Law: Current Through Each Component: V I R 15

Summary: In this presentation, We have seen The statements of q Ohm’s Law The concepts of q Nodes, branches, series, parallel circuits q Kirchhoff’s voltage law q Kirchhoff’s current law The procedure to solve q Series circuits q Parallel circuits NOW, TRY THE FOLLOWING PROBLEMS 16

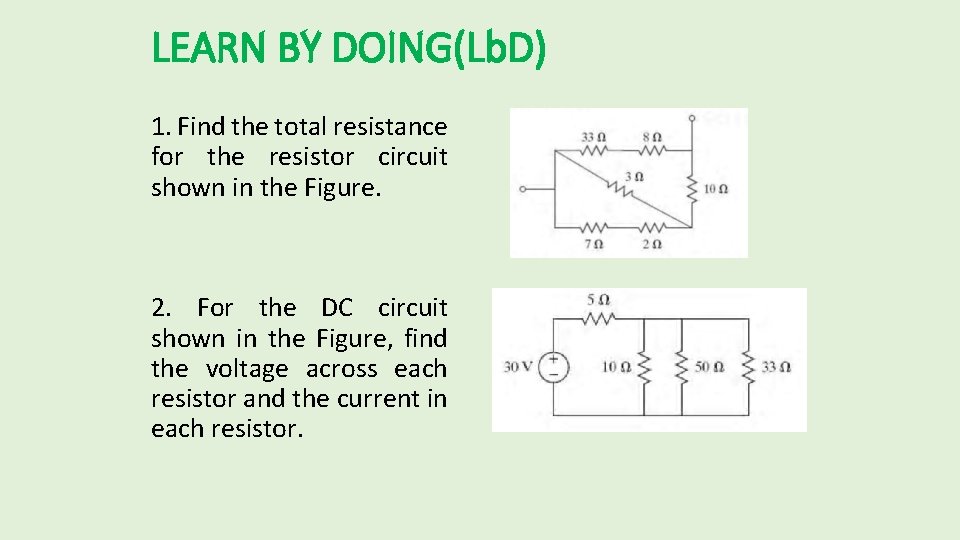
LEARN BY DOING(Lb. D) 1. Find the total resistance for the resistor circuit shown in the Figure. 2. For the DC circuit shown in the Figure, find the voltage across each resistor and the current in each resistor.

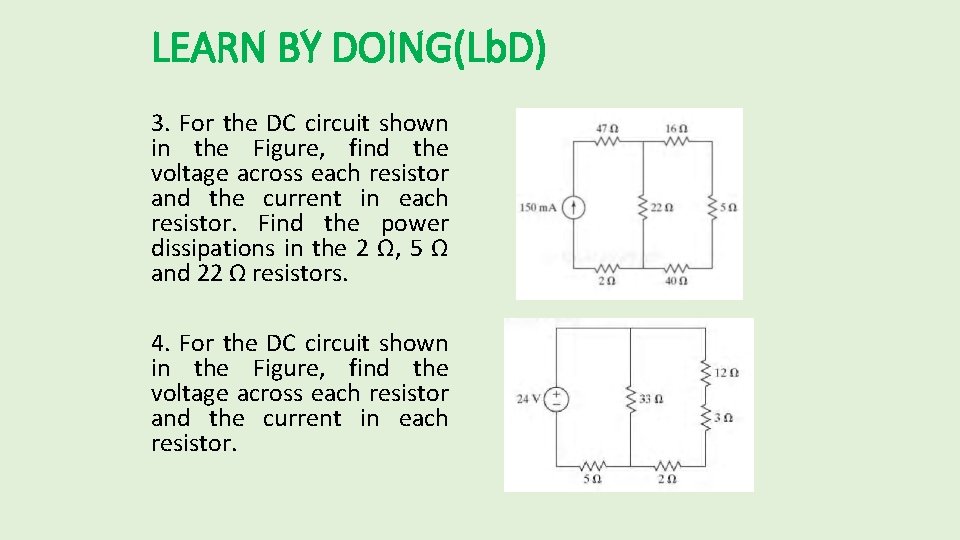
LEARN BY DOING(Lb. D) 3. For the DC circuit shown in the Figure, find the voltage across each resistor and the current in each resistor. Find the power dissipations in the 2 Ω, 5 Ω and 22 Ω resistors. 4. For the DC circuit shown in the Figure, find the voltage across each resistor and the current in each resistor.