Electric Potential Energy Electric Potential Honors Physics Mr

Electric Potential Energy & Electric Potential Honors Physics Mr. Kuffer

We Know… Coulomb’s Law Q 1 r Q 2 If either Q 1 or Q 2 increases the Force increases If either Q 1 or Q 2 decreases the Force decreases If r, the distance between the two charges, increases the force decreases If r, the distance between the two charges, decreases the force increases Because r appears as 1/r 2 the dependence on r is strong

We know… Coulomb’s Law Q 1 r Q 2 Double r. F decreases by a factor of 4 If r -> r/3 F increases by a factor of 9 If r decreases to ¼ of its value, F becomes 16 times as large

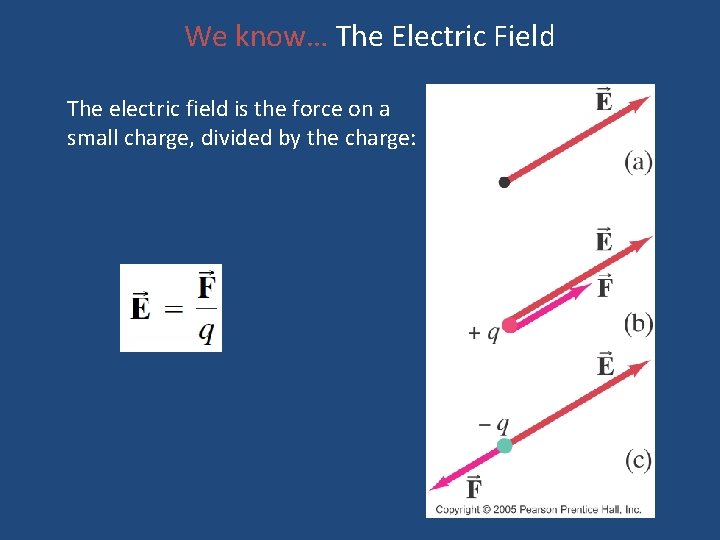
We know… The Electric Field The electric field is the force on a small charge, divided by the charge:

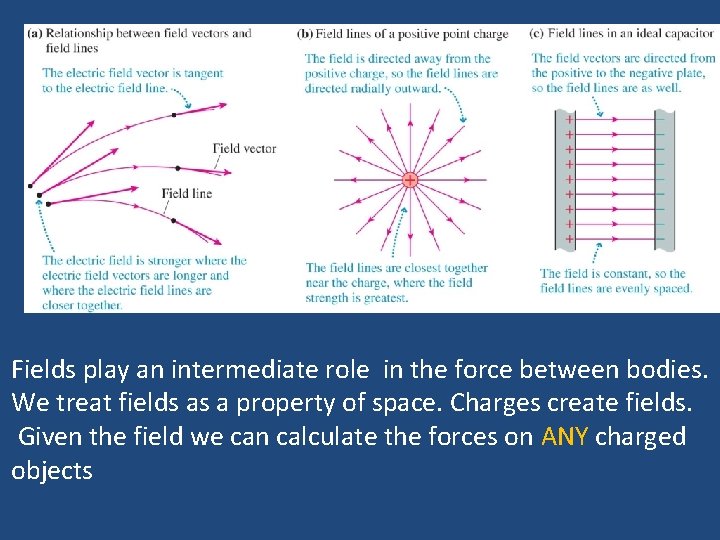
Fields play an intermediate role in the force between bodies. We treat fields as a property of space. Charges create fields. Given the field we can calculate the forces on ANY charged objects

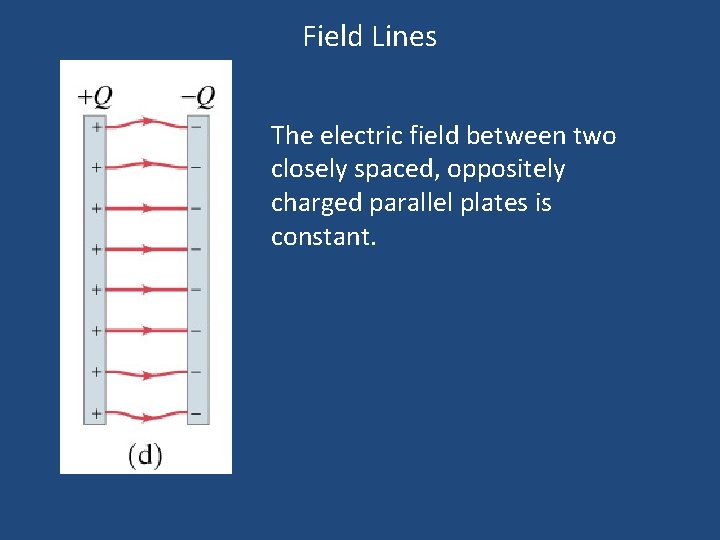
Field Lines The electric field between two closely spaced, oppositely charged parallel plates is constant.

Today’s Topics • Electric Potential Energy • Electric Potential • Electric Equi-potential Lines

Recall… Work • You do work when you push an object up a hill • The longer the hill the more work you do: more distance • The taller the hill, the more work you do: more force The work, W, done on an object by an agent exerting a constant force is the product of the component of the force in the direction of the displacement and the magnitude of the displacement

Energy is capacity to do work note Ep aka UG • Gravitational Potential Energy • Kinetic Energy • Energy can be converted into other forms of energy • When we do work on any object we transfer energy to it • Energy cannot be created or destroyed

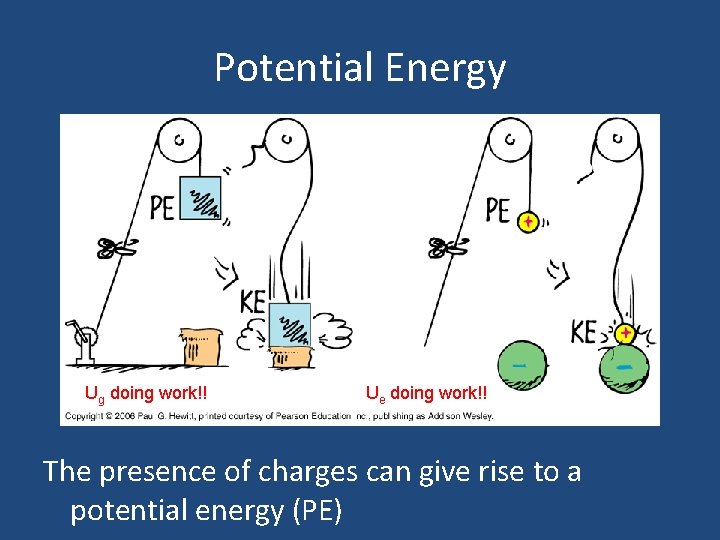
Potential Energy Ug doing work!! Ue doing work!! The presence of charges can give rise to a potential energy (PE)

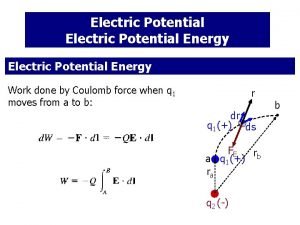
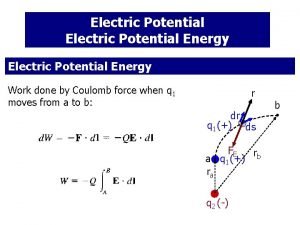
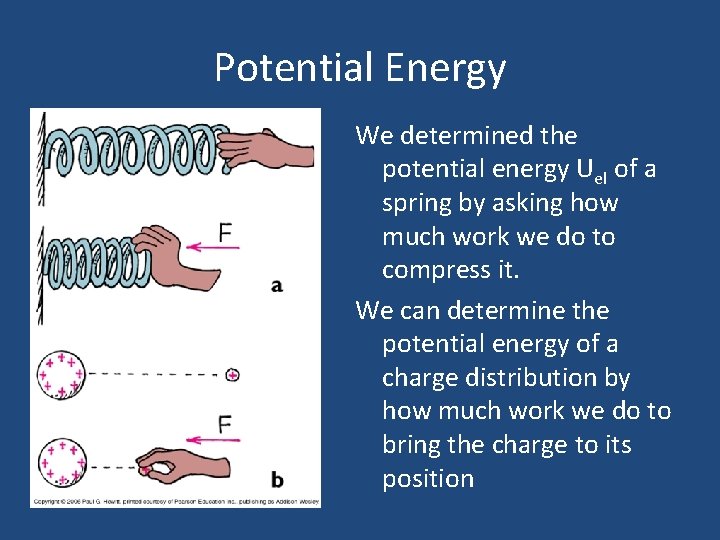
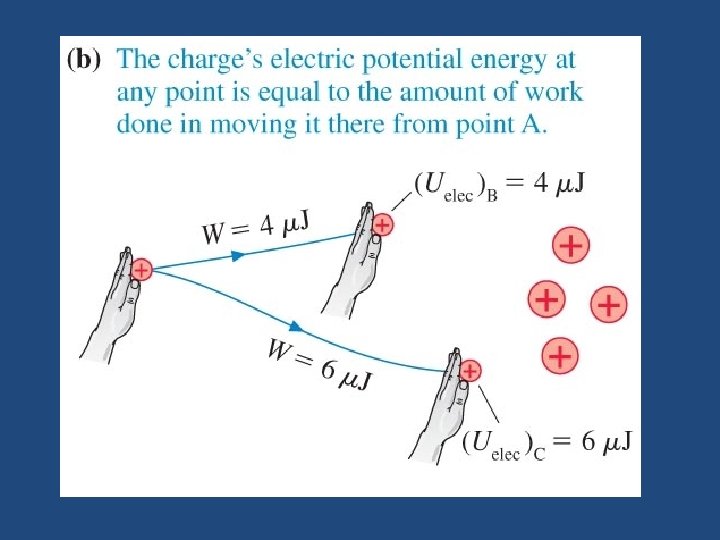
Potential Energy We determined the potential energy Uel of a spring by asking how much work we do to compress it. We can determine the potential energy of a charge distribution by how much work we do to bring the charge to its position

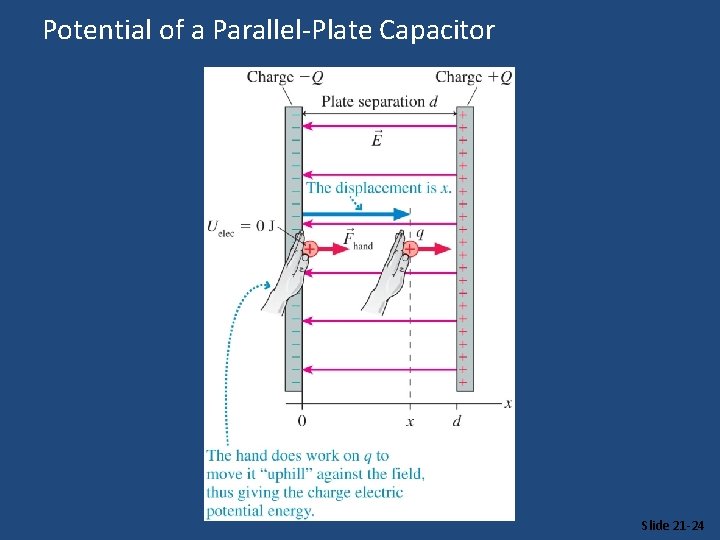
Potential of a Parallel-Plate Capacitor Slide 21 -24

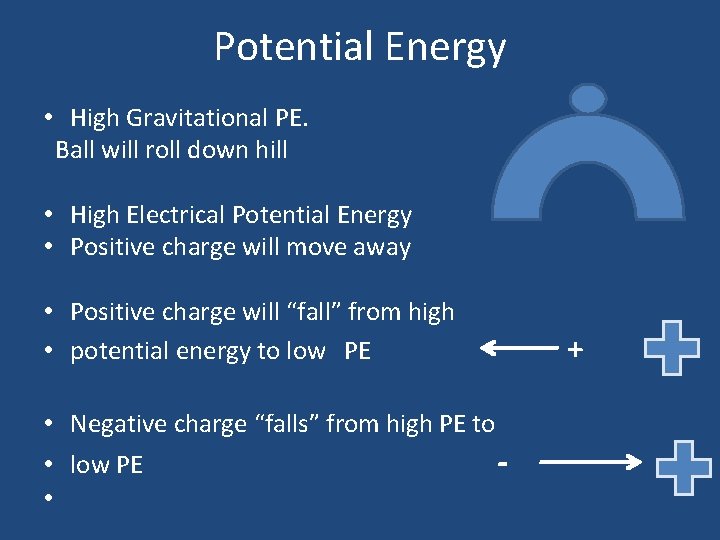
Potential Energy • High Gravitational PE. Ball will roll down hill • High Electrical Potential Energy • Positive charge will move away • Positive charge will “fall” from high • potential energy to low PE • Negative charge “falls” from high PE to • low PE • + -

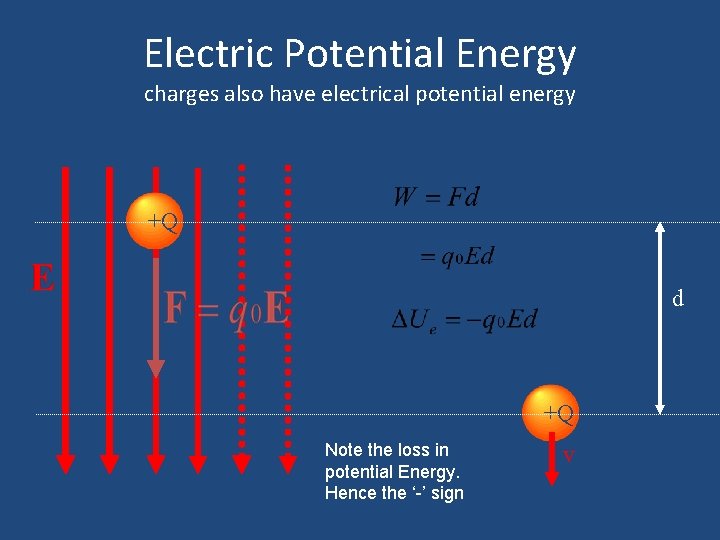
Electric Potential Energy charges also have electrical potential energy +Q d +Q Note the loss in potential Energy. Hence the ‘-’ sign v

Electric Potential Energy • Work done (by electric field) on charged particle is q. Ed • Particle has gained Kinetic Energy (q. Ed) • Particle must therefore have lost Potential Energy U=-q. Ed

Electrostatic Potential Energy Change in electric potential energy is work done against electric force (from b to a): PEa – PEb = q. Ed a--Compare Ug b--- Ug = mg (a-b) =mgh

Electric Potential (Not Electric Potential Energy) • Just as Electric field depends on space and allows us to compute force on any charge, Electric Potential depends on space and allows us to calculate Uelec for any charge.

Electric Potential compare with the Electric Field and Coulomb Force If we know the potential field this allows us to calculate changes in potential energy for any charge introduced

Electrostatic Potential Energy and Potential Difference Electric potential is defined as potential energy per unit charge: Unit of electric potential: the volt (V). 1 V = I J/C.

Greater at B, Greater yet at C

Ue= q. V

U e= q V Ue(B) = 10 n. C * 400 V

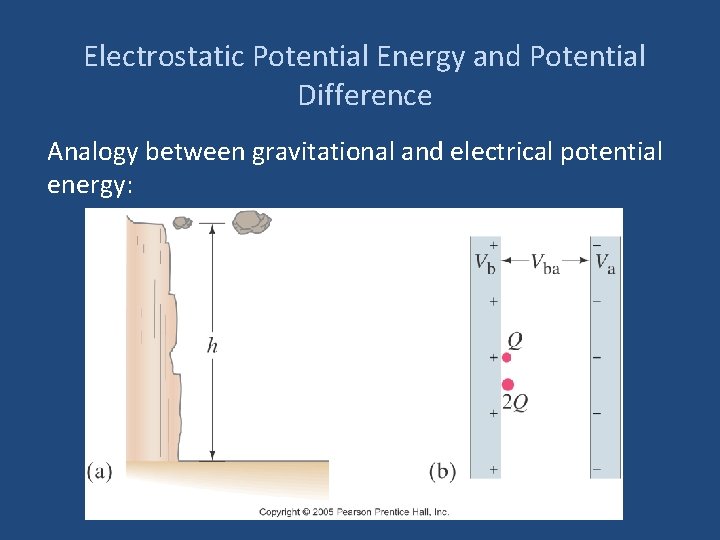
Electrostatic Potential Energy and Potential Difference Analogy between gravitational and electrical potential energy:

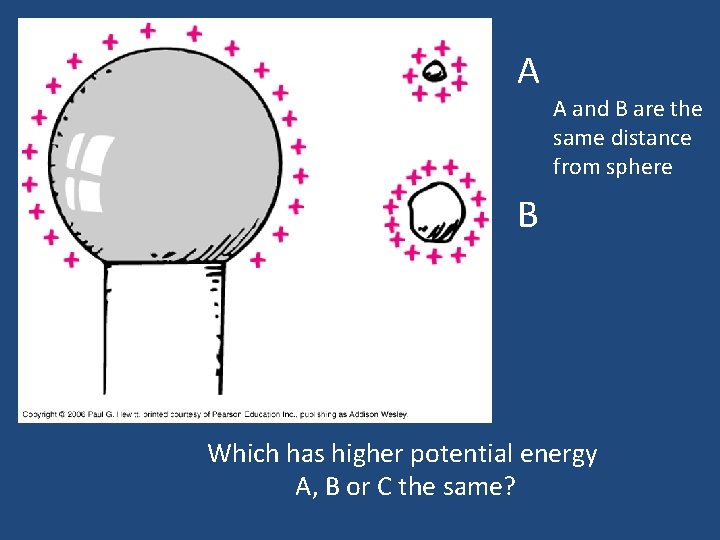
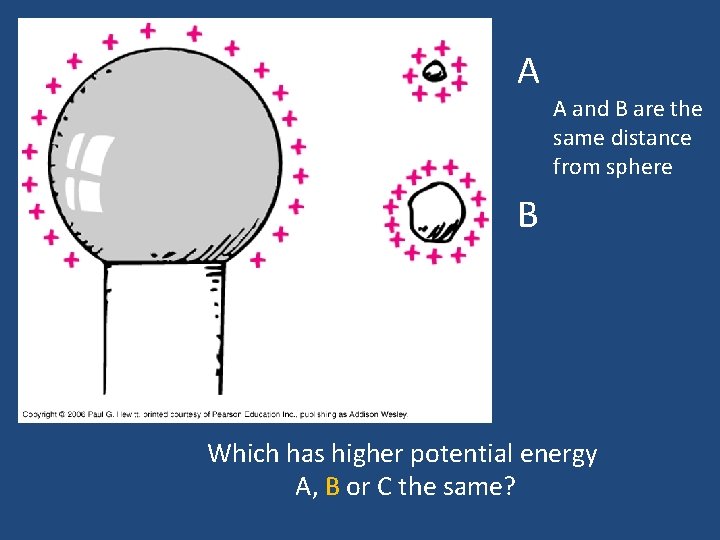
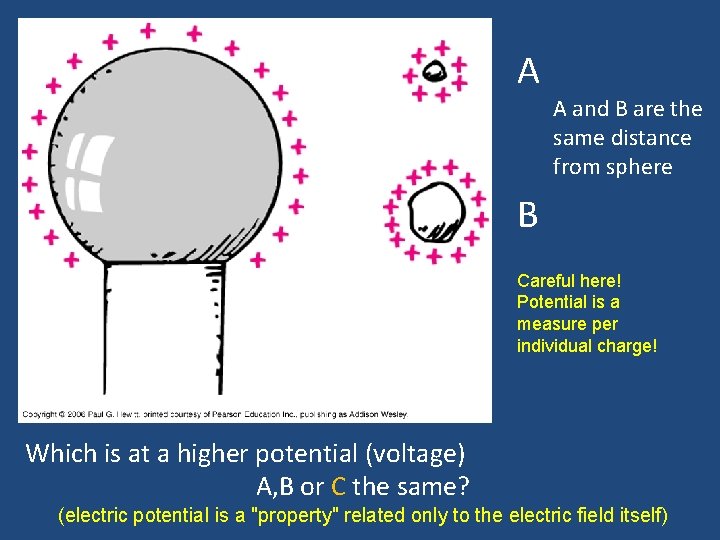
A A and B are the same distance from sphere B Which has higher potential energy A, B or C the same?

A A and B are the same distance from sphere B Which has higher potential energy A, B or C the same?

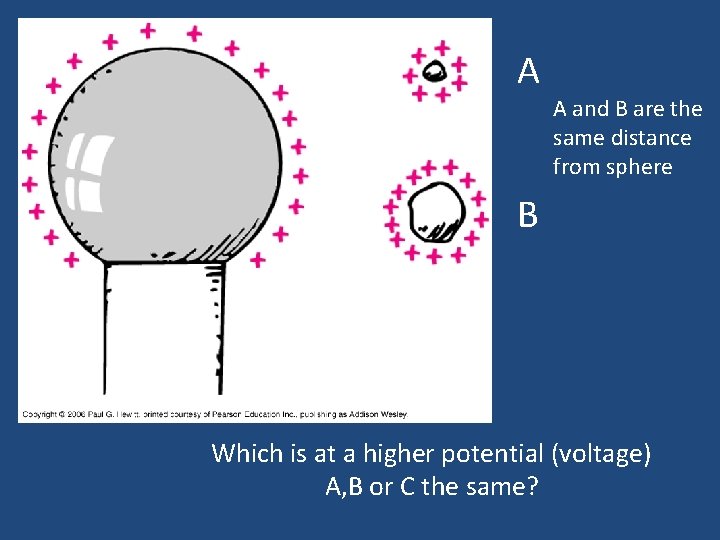
A A and B are the same distance from sphere B Which is at a higher potential (voltage) A, B or C the same?

A A and B are the same distance from sphere B Careful here! Potential is a measure per individual charge! Which is at a higher potential (voltage) A, B or C the same? (electric potential is a "property" related only to the electric field itself)

Electrostatic Potential Energy and Potential Difference Only changes in potential can be measured, allowing free assignment of V = 0… where there is no change there is no potential difference. Vba = Vb – Va = Ue(b) –Ue (a) q Therefore Potential (V) is unaffected by position change within equipotential surfaces! For Potential Difference… defining ‘zero’ is arbitrary… just like choosing a frame of reference for Ug

Electric Potential is a scalar it is defined everywhere it doesn’t depend on a charge being there but it does not have any direction

Super Fun Review Challenge!

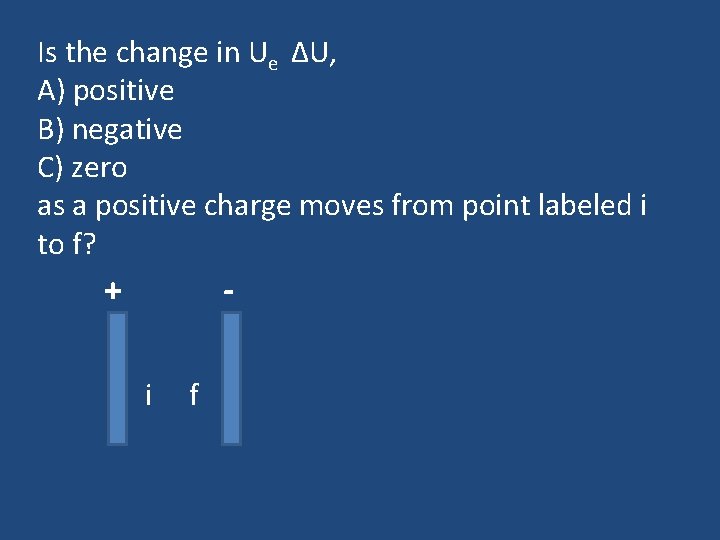
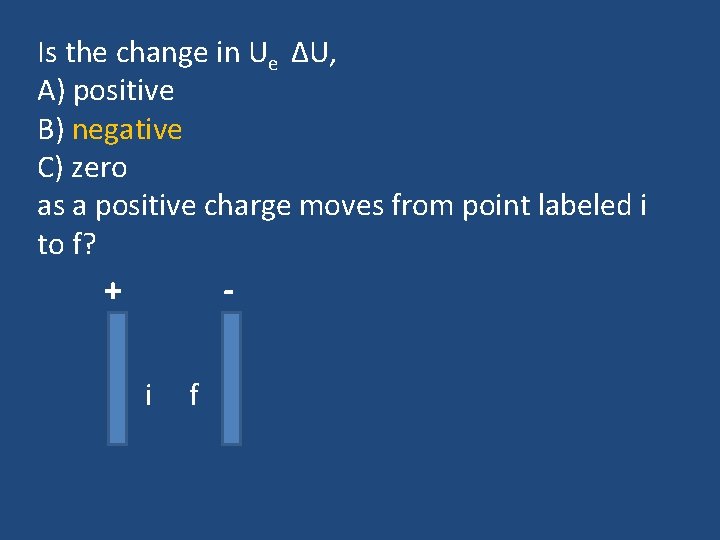
Is the change in Ue ΔU, A) positive B) negative C) zero as a positive charge moves from point labeled i to f? + i f

Is the change in Ue ΔU, A) positive B) negative C) zero as a positive charge moves from point labeled i to f? + i f

Is the change in Ue ΔU, A) positive B) negative C) zero as a negative charge moves from point labeled i to f? + i f

Is the change in Ue ΔU, A) positive B) negative C) zero as a negative charge moves from point labeled i to f? + i f

Is the change in Ue ΔU, A) positive B) negative C) zero as a positive charge moves from point labeled i to f? + i f

Is the change in Ue ΔU, A) positive B) negative C) zero as a positive charge moves from point labeled i to f? + i f

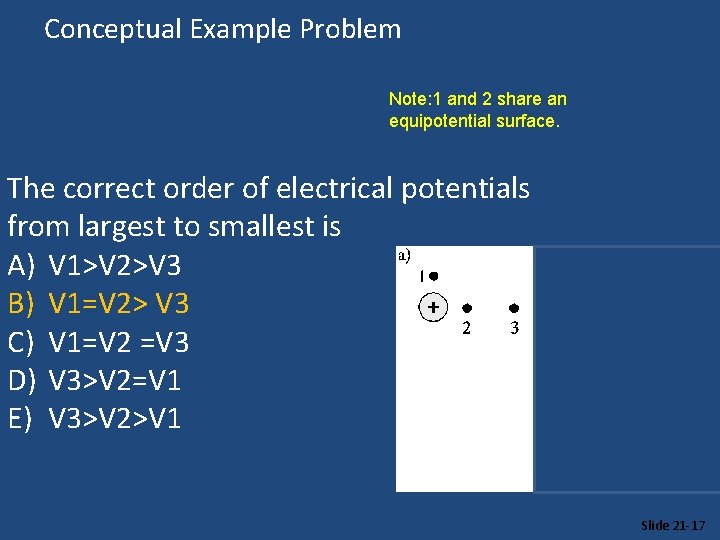
Conceptual Example Problem Note: q 1, q 2, & q 3 are positive test charges The correct order of electrical potentials from largest to smallest is A) V 1>V 2>V 3 B) V 1=V 2> V 3 C) V 1=V 2 =V 3 D) V 3>V 2=V 1 E) V 3>V 2>V 1 Slide 21 -17

Conceptual Example Problem Note: 1 and 2 share an equipotential surface. The correct order of electrical potentials from largest to smallest is A) V 1>V 2>V 3 B) V 1=V 2> V 3 C) V 1=V 2 =V 3 D) V 3>V 2=V 1 E) V 3>V 2>V 1 Slide 21 -17

Conceptual Example Problem The correct order of electrical potentials from largest to smallest is A) V 1>V 2>V 3 B) V 1=V 2> V 3 Note: q , & q are positive test charges C) V 1=V 2 =V 3 D) V 3>V 2=V 1 E) V 3>V 2>V 1 1 2 3 Slide 21 -17

Conceptual Example Problem The correct order of electrical potentials from largest to smallest is A) V 1>V 2>V 3 B) V 1=V 2> V 3 Note: We are asked about the Electric Potential… not C) V 1=V 2 =V 3 the Force the charge Feels! D) V 3>V 2=V 1 E) V 3>V 2>V 1 Slide 21 -17

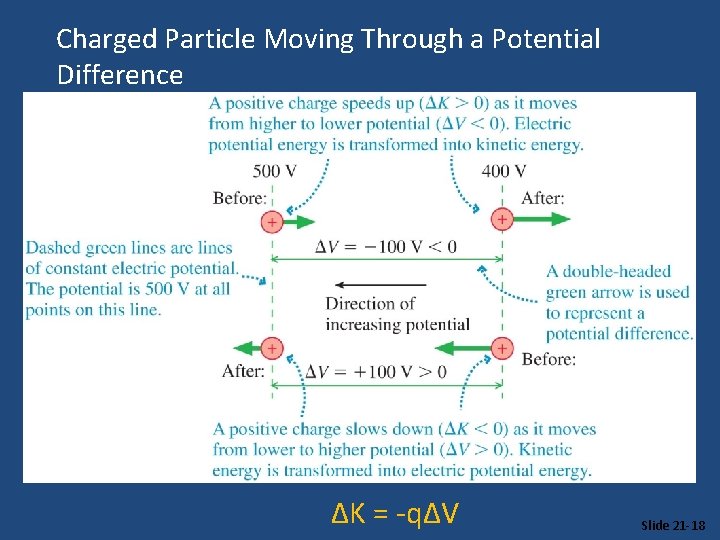
Energy Conservation in Electric Potentials • Just as for mechanical systems Energy is conserved. We can change potential energy to kinetic energy and vice versa. • Kf + q. Vf = Ki + q. Vi • Kf –Ki = q. Vi –q Vf =-q(Vf –Vi) ΔK = -qΔV The more Potential is lost… the more Kinetic is gained

Charged Particle Moving Through a Potential Difference ΔK = -qΔV Slide 21 -18

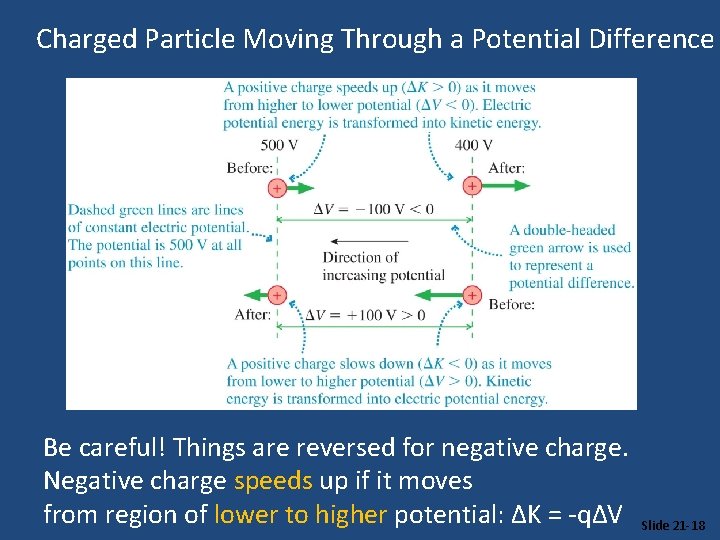
Charged Particle Moving Through a Potential Difference Be careful! Things are reversed for negative charge. Negative charge speeds up if it moves from region of lower to higher potential: ΔK = -qΔV Slide 21 -18

The Electron Volt, a Unit of Energy One electron volt (e. V) is the energy (not charge) gained by an electron moving through a potential difference of one volt.

Slide 21 -19

Example Problem A proton has a speed of 3. 5 x 105 m/s at a point where the electrical potential is 600 V. It moves through a point where the electric potential is 1000 V. What is its speed at this second point? Slide 21 -20