Electric Forces and Fields GIANCOLI CHAPTER 16 Electric


























- Slides: 34

Electric Forces and Fields GIANCOLI- CHAPTER 16

Electric Charge Electric charge is conserved Electric Charge is quantized One unit of charge : e= 1. 60219 x 10 -19 C C stands for Coulomb, the unit of electric charge A proton has a charge of +1. 60 x 10 -19 C An electron has a charge of -1. 60 x 10 -19 C

Conductors & Insulators Conductors: Materials in which electric charges move freely Examples: most metals Insulators: Materials in which electric charges do not move freely Examples: Plastic, glass, silk, rubber

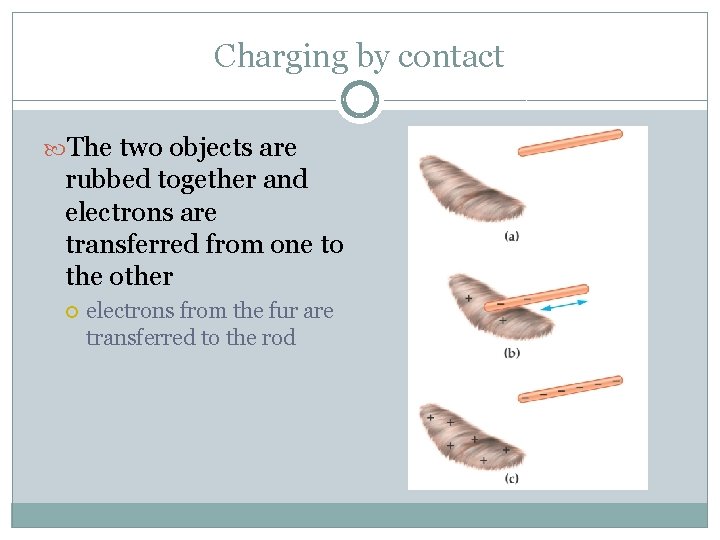
Charging by contact The two objects are rubbed together and electrons are transferred from one to the other electrons from the fur are transferred to the rod

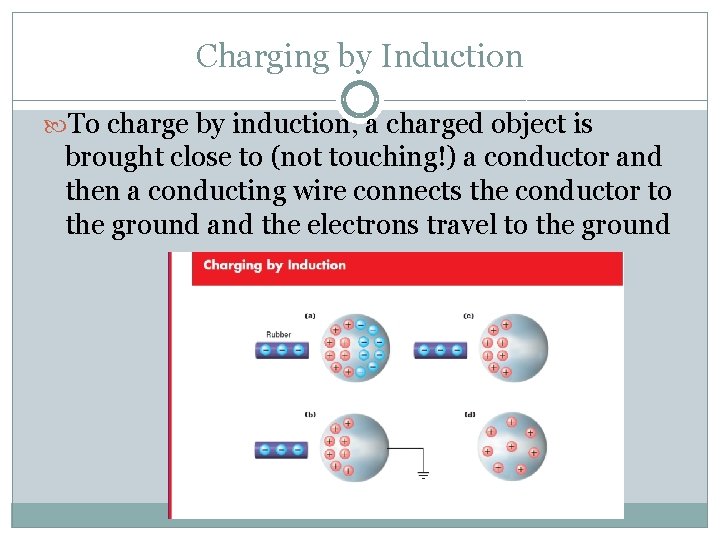
Charging by Induction To charge by induction, a charged object is brought close to (not touching!) a conductor and then a conducting wire connects the conductor to the ground and the electrons travel to the ground

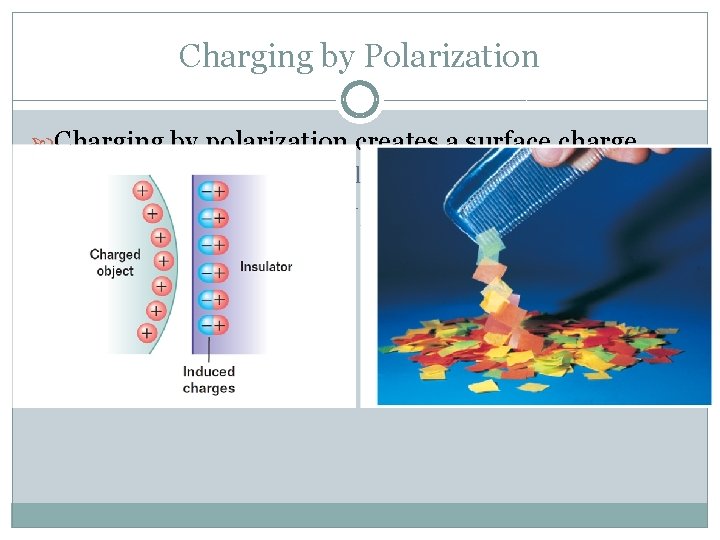
Charging by Polarization Charging by polarization creates a surface charge A charged object is brought close to an insulator and the electrons and protons realign themselves to create one side that is more positive and one that is more negative

Coulomb’s Law describes the mathematical relationship between electric force, distance and electric charge for two objects k. C= 8. 99 x 109 Nm 2 C 2 Electric force= Coulomb’s Constant x (charge 1)(charge 2) distance 2

Coulomb’s Law Remember that force is a vector! For problems involving two charges, the direction is either “attractive” or “repulsive” the direction of the force between a positive charge and negative charge is attractive a the direction of the force between two negative charges is repulsive

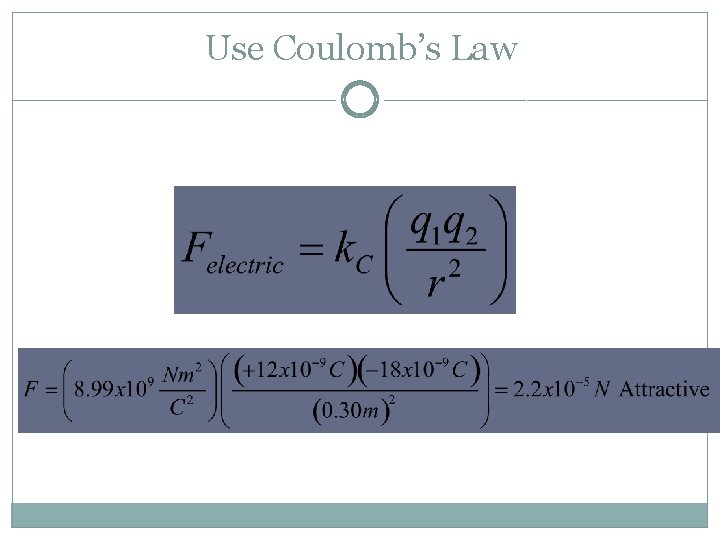
Example Problem Two identical conducting spheres are placed with their centers 0. 30 m apart. One is given a charge of +12 x 10 -9 C and the other is given a charge of -18 x 10 -9 C A. Find the electric force exerted on one sphere by the other B. The spheres are connected by a conducting wire. After equilibrium has occurred, find the electric force between the two spheres.

Use Coulomb’s Law

What does it mean “after equilibrium has occurred”? The charge on each sphere is the same

Three charges in a line Three charges are arranged in a line as shown below. The distance between Q 1 and Q 2 is 0. 35 m and the distance between Q 2 and Q 3 is 0. 45 m. What is the net electrostatic force acting on Q 3? Q 1 +4 µC Q 2 -5 µC Q 3 +8µC

Find the force acting on Q 3 from Q 1 Find the force acting on Q 3 from Q 2 Net force acting on Q 3= 1. 33 N Left

Two Dimensional Problem Three charges are arranged in a triangular pattern as shown below. The distance between Q 1 and Q 2 is 0. 35 m and the distance between Q 2 and Q 3 is 0. 45 m. Find the net electrostatic force on Q 2 Q 1 +4 µC Q 2 -5 µC Q 3 +8µC

Solving the Problem We already have the numerical values for the force acting on Q 2 from Q 3…but the direction is different F 32= 1. 78 N Right Find the force from Q 1 on Q 2

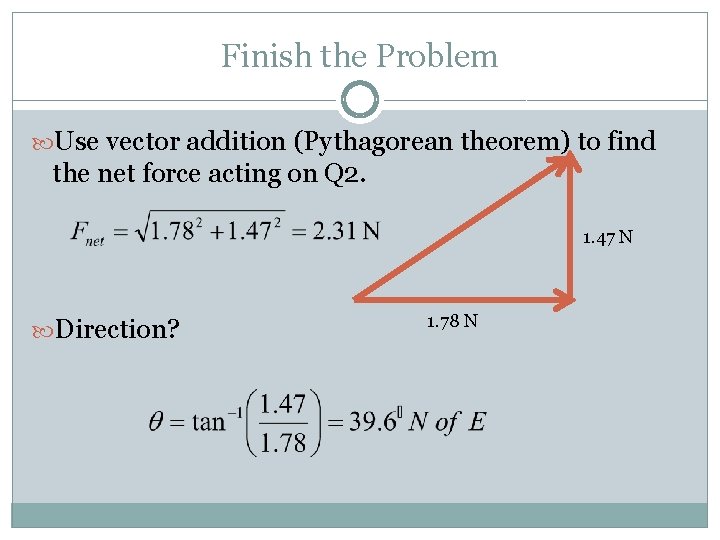
Finish the Problem Use vector addition (Pythagorean theorem) to find the net force acting on Q 2. 1. 47 N Direction? 1. 78 N

Electric Field �Electric force, like gravitational force, is a field force Remember: Field forces can act through space even when there is no physical contact between the objects involved �A charged object has an electric field in the space around it

Electric Field Lines �Electric Field Lines point in the direction of the electric field �The number and spacing of field lines is proportional to the electric field strength The electric field is strong where the field lines are close together and weaker when they are far apart

Electric Field Lines �The lines for a positive charge point away from the charge �The lines for a negative charge point towards the charge

Electric Field Lines �This diagram shows the electric field lines for two equal and opposite point charges Notice that the lines begin on the positive charge and end on the negative charge

Electric Field Lines �This diagram shows the electric field lines for two positive point charges Notice that the same number of lines emerges from each charge because they are equal in magnitude

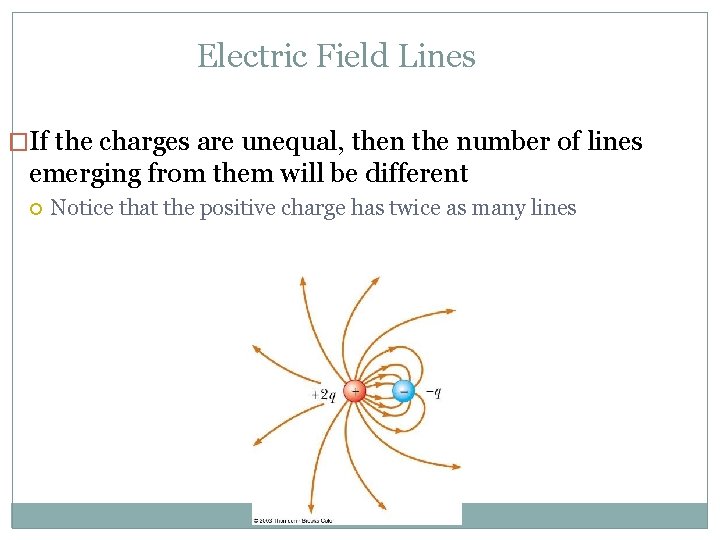
Electric Field Lines �If the charges are unequal, then the number of lines emerging from them will be different Notice that the positive charge has twice as many lines

Calculating Electric Field Strength �The equation for the electric field produced by a point charge is: Kc=9 x 109 Nm 2/C 2 , r is the distance from the charge and q is the charge producing the field The unit for E is N/C �Electric field strength is a vector!! If q is positive, then E is directed away from q If q is negative, then E is directed toward q

Calculating the force from an electric field �If a charged object is placed in an electric field, we can calculate the force acting on it from the electric field �Remember that F is a vector!!

Sample Problem p. 647 #3 �An electric field of 2. 0 x 104 N/C is directed along the positive x-axis a. What is the electric force on an electron in this field? b. What is the electric force on a proton in this field?

Sample Problem p. 647 #3 �E= 2. 0 x 104 N/C , q= 1. 6 x 10 -19 C �F=q. E= 3. 2 x 10 -15 N for both the electron and the proton �What about the direction? The electric field is pointing along the positive x axis (to the right) which means there’s a positive charge to the left E field +

For the proton �Since the electric field is pointing to the right, if you put a proton in it, the proton will want to move away towards the right and the direction of the force on it will be to the right + + F �Answer: 3. 2 x 10 -15 N along the positive x axis (to the right)

For the electron Since there’s a positive charge causing the electric field to point towards the right, an electron would feel attracted to the positive charge. Therefore, the force acting on it is toward the left Answer: 3. 2 x 10 -15 N along the negative x axis (to the left) + F -

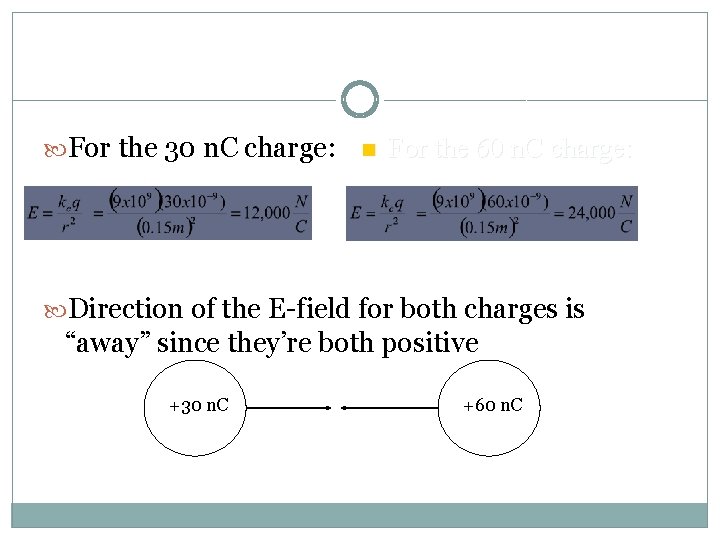
Sample Problem Find the electric field at a point midway between two charges of +30 n. C and 60 n. C separated by a distance of 30. 0 cm +30 n. C +60 n. C

For the 30 n. C charge: n For the 60 n. C charge: Direction of the E-field for both charges is “away” since they’re both positive +30 n. C +60 n. C

Which one will win? At the midway point, the 30 n. C charge’s field strength is 12000 N/C toward the 60 n. C charge and the 60 n. C charge’s field strength is 24, 000 N/C toward the 30 n. C charge. The 60 n. C charge will win. Since the field’s point in opposite directions, you have to subtract Answer: 12, 000 N/C toward the 30 n. C charge

Sample Problem A constant electric field directed along the positive x- axis has a strength of 2. 0 x 103 N/C. Find the electric force exerted on a proton by the field Find the acceleration of the proton

Answer F=q. E=(1. 6 x 10 -19 C)(2. 0 x 103 N/C)= 3. 2 x 10 -16 N Direction? E field + + F Answer: 3. 2 x 10 -16 N along the positive x-axis (to the right)

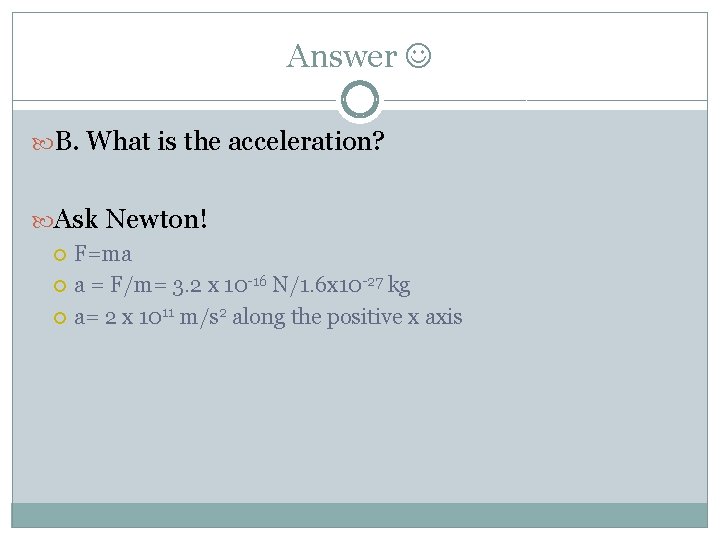
Answer B. What is the acceleration? Ask Newton! F=ma a = F/m= 3. 2 x 10 -16 N/1. 6 x 10 -27 kg a= 2 x 1011 m/s 2 along the positive x axis