Electric field Chapter 22 Week2 Electric Fields 22

Electric field Chapter 22 Week-2

Electric Fields (22 -1) In this chapter we will introduce the concept of an electric field. As long as charges are stationary Coulomb’s law described adequately the forces among charges. If the charges are not stationary we must use an alternative approach by introducing the electric field (symbol ). In connection with the electric field, the following topics will be covered: -Calculate the electric field generated by a point charge. -Using the principle of superposition determine the electric field created by a collection of point charges as well as continuous charge distributions. -Once the electric field at a point P is known we will be calculate the electric force on any charge placed at P Define the notion of an “electric dipole”. Determine the net force , the net torque, exerted on an electric dipole by a uniform electric field, as well as the dipole potential energy.

Fields n Imagine an object is placed at a particular point in n n space. When placed there, the object experiences a force F. We may not know WHY there is a force on the object, although we usually will. Suppose further that if we double some property of the object (mass, charge, …) then the force is found to double as well. Then the object is said to be in a force field. The strength of the field (field strength) is defined as the ratio of the force to the property that we are dealing with.

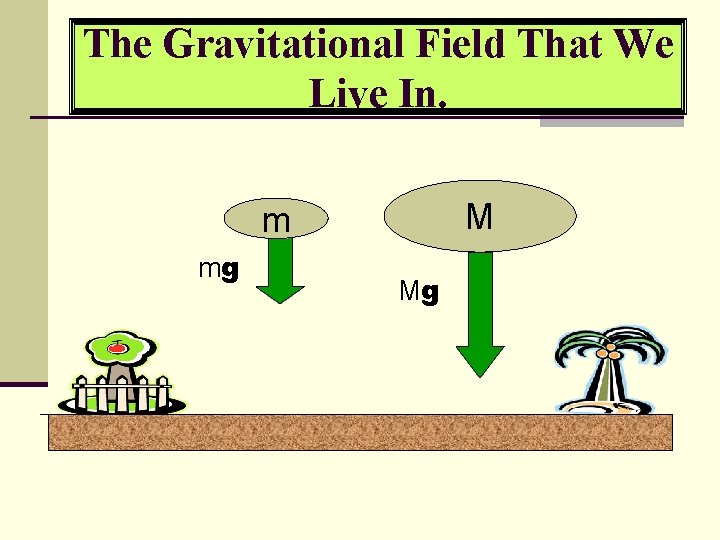
Example – Gravitational Field. n Property is MASS (m). n Force is mg. n Field strength is defined as Force/Property

The Gravitational Field That We Live In. M m mg Mg

Properties of a force field n It is a property of the position in space. n There is a cause but that cause may not be known. n The force on an object is usually proportional to some property of an object which is placed into the field.

Mysterious Force F

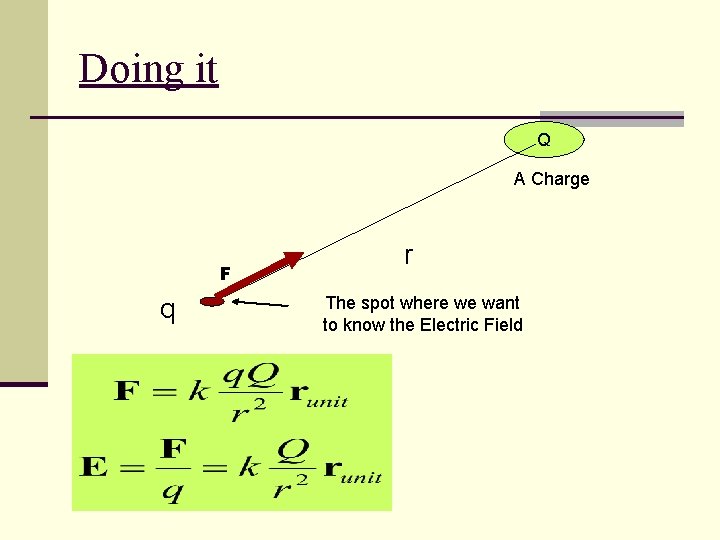
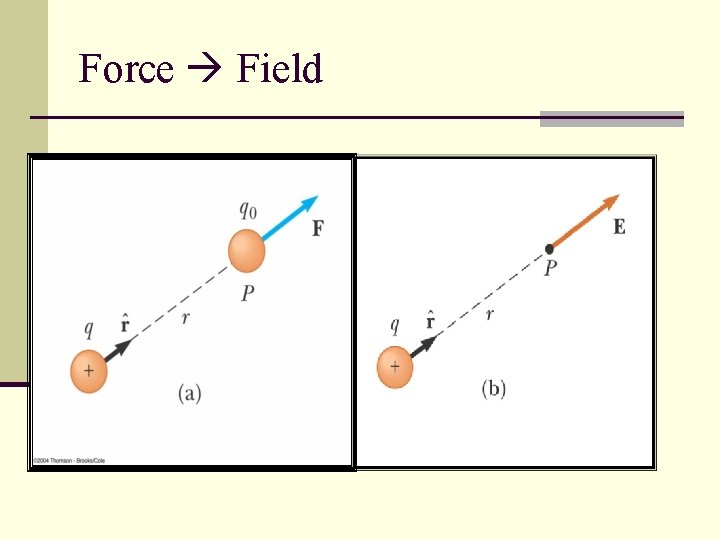
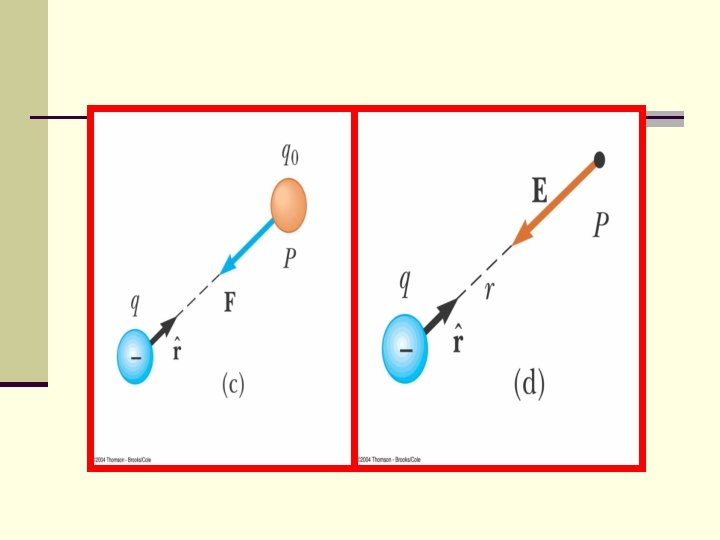
Electric Field n If a charge Q is in an electric field E then it will experience a force F. n The Electric Field is defined as the force per unit charge at the point. n Electric fields are caused by charges and consequently we can use Coulombs law to calculate it. n For multiple charges, add the fields as VECTORS.

Two Charges

Doing it Q A Charge F q r The spot where we want to know the Electric Field

General-

Force Field

Two Charges What is the Electric Field at Point P?

qo. P q (22 -4) r

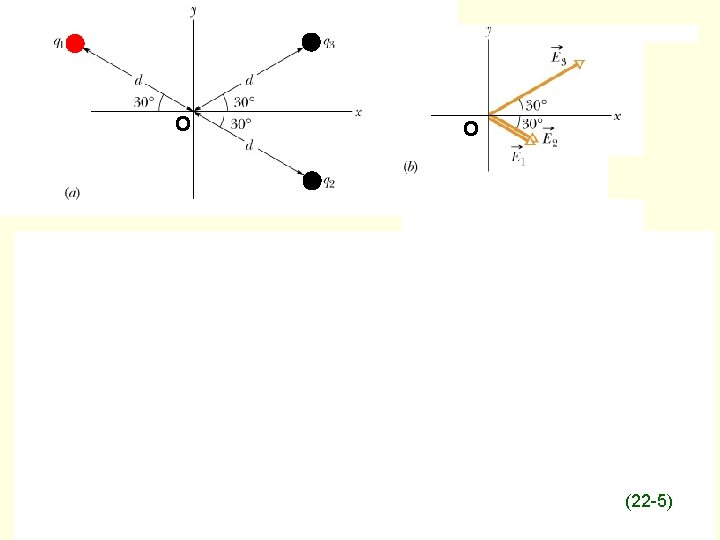
O O (22 -5)

What is the electric field at the center of the square array?

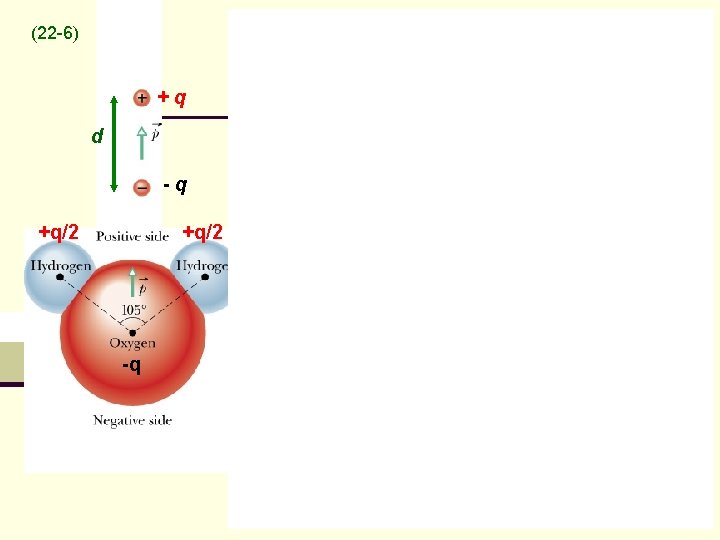
(22 -6) +q d -q +q/2 -q

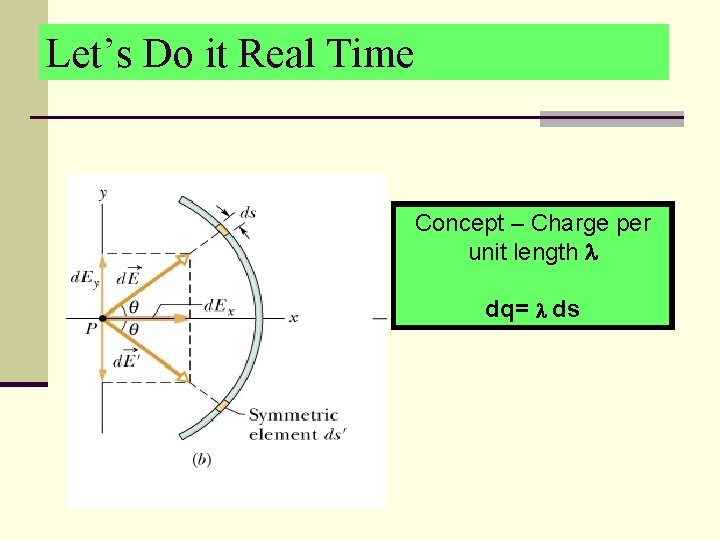
Kinds of continuously distributed charges n Line of charge n m or sometimes l = the charge per unit length. n dq=mds (ds= differential of length along the line) n Area n s = charge per unit area n dq=sd. A n d. A = dxdy (rectangular coordinates) n d. A= 2 prdr for elemental ring of charge n Volume n r=charge per unit volume n dq=rd. V n d. V=dxdydz or 4 pr 2 dr or some other expressions we will look at later.

Kinds of continuously distributed charges n Line of charge n l = the charge per unit length. n dq= lds (ds= differential of length along the line) n Area n s = charge per unit area n dq=sd. A n d. A = dxdy (rectangular coordinates) n d. A= 2 prdr for elemental ring of charge n Volume n r=charge per unit volume n dq=rd. V n d. V=dxdydz or 4 pr 2 dr or some other expressions we will look at later.

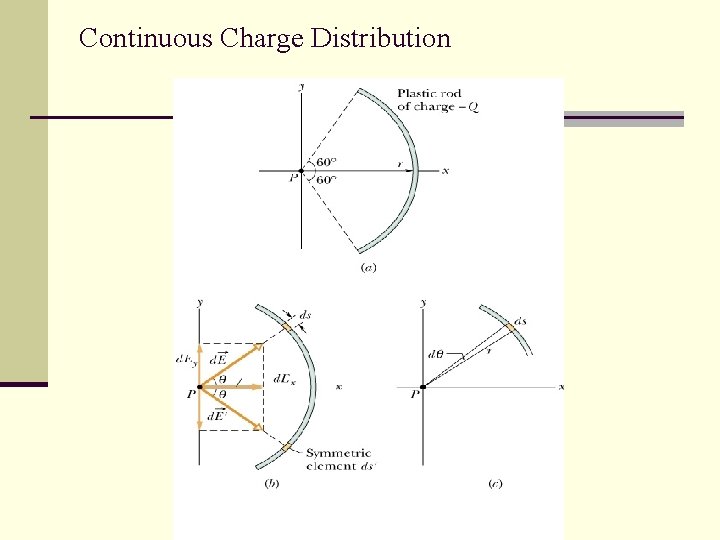
Continuous Charge Distribution

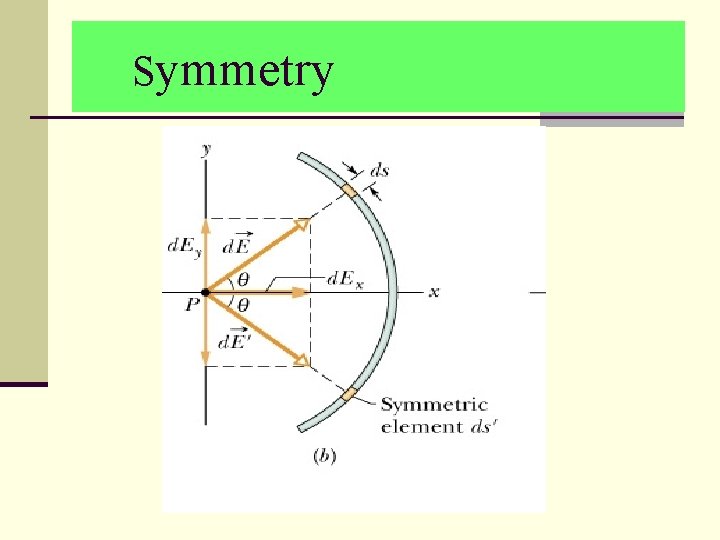
Symmetry

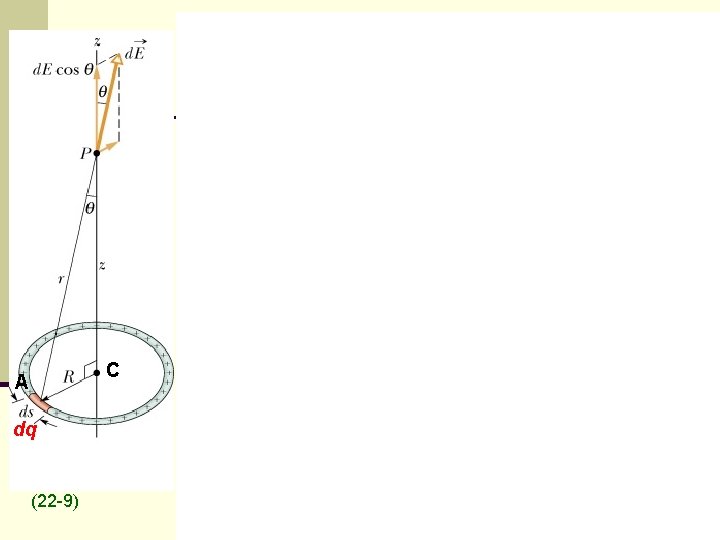
Let’s Do it Real Time Concept – Charge per unit length dq= ds

The math Why?

C A dq (22 -9)

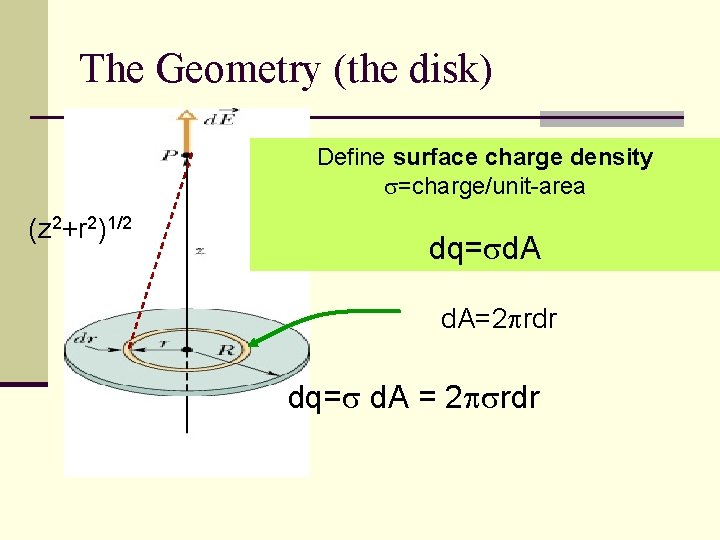
The Geometry (the disk) Define surface charge density s=charge/unit-area (z 2+r 2)1/2 dq=sd. A=2 prdr dq=s d. A = 2 psrdr

(z 2+r 2)1/2 q

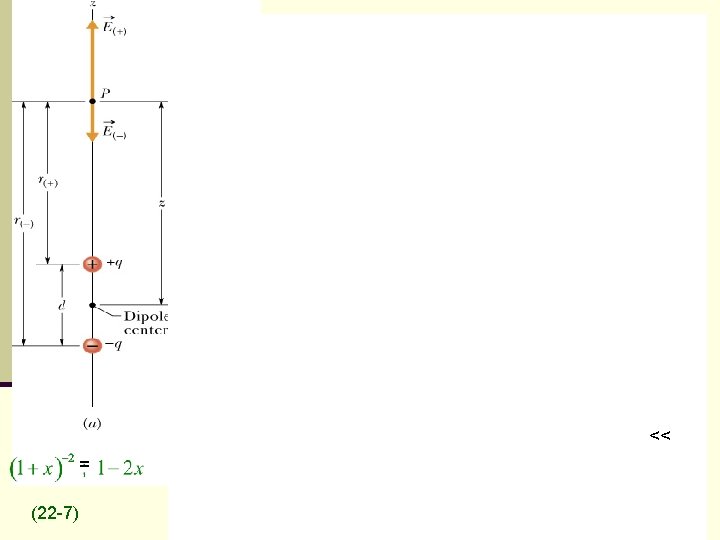
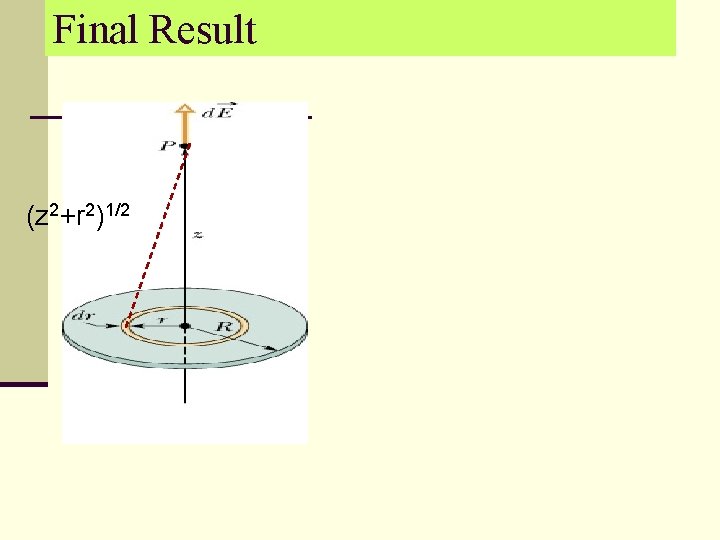
Final Result (z 2+r 2)1/2

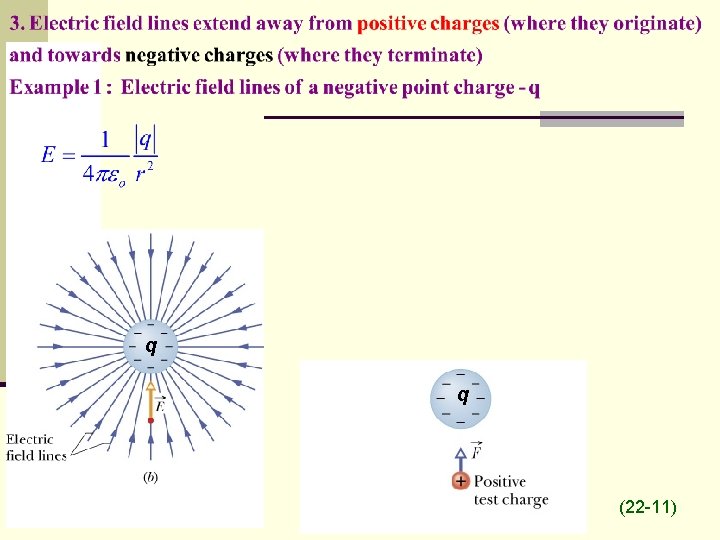
q q (22 -11)

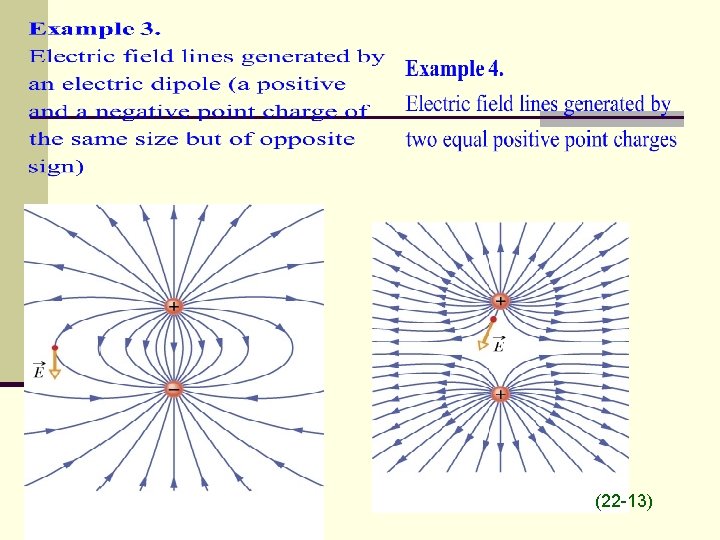
(22 -13)

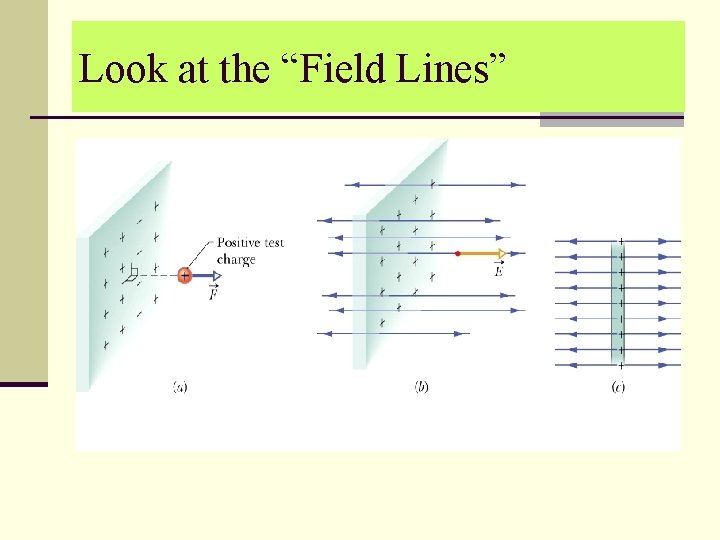
Look at the “Field Lines”

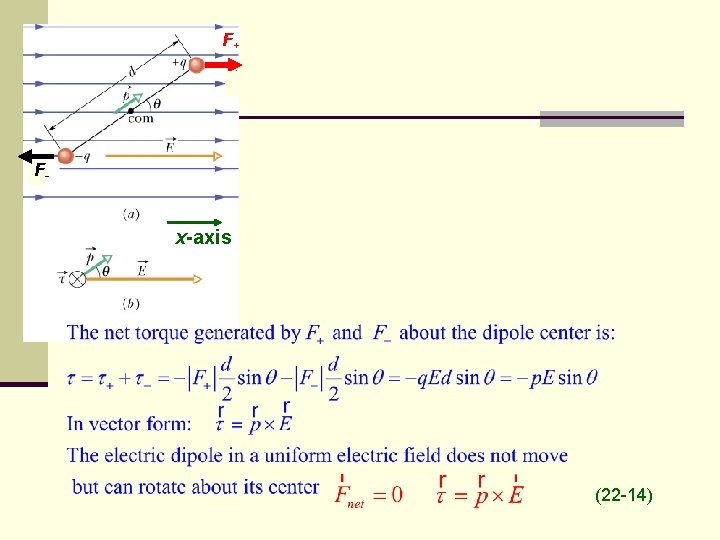
F+ F- x-axis (22 -14)

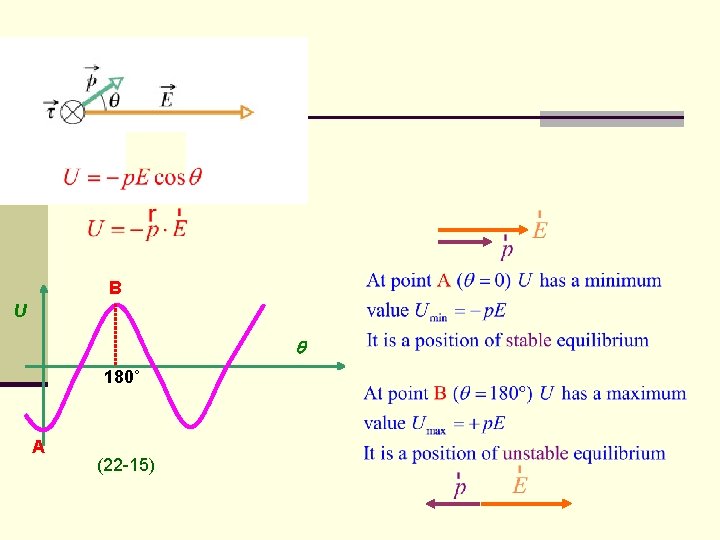
B U 180˚ A (22 -15)

Fig. a Fig. b (22 -16)

What did we learn in this chapter? ? n We introduced the concept of the Electric FIELD We may not know what causes the field. (The evil Emperor Ming) n If we know where all the charges are we can CALCULATE E. n E is a VECTOR. n The equation for E is the same as for the force on a charge from Coulomb’s Law but divided by the “q of the test charge”. n

What else did we learn in this chapter? n We introduced continuous distributions of charge rather than individual discrete charges. n Instead of adding the individual charges we must INTEGRATE the (dq)s. n There are three kinds of continuously distributed charges.

Kinds of continuously distributed charges n Line of charge n l = the charge per unit length. n dq= lds (ds= differential of length along the line) n Area n s = charge per unit area n dq=sd. A n d. A = dxdy (rectangular coordinates) n d. A= 2 prdr for elemental ring of charge n Volume n r=charge per unit volume n dq=rd. V n d. V=dxdydz or 4 pr 2 dr or some other expressions we will look at later.

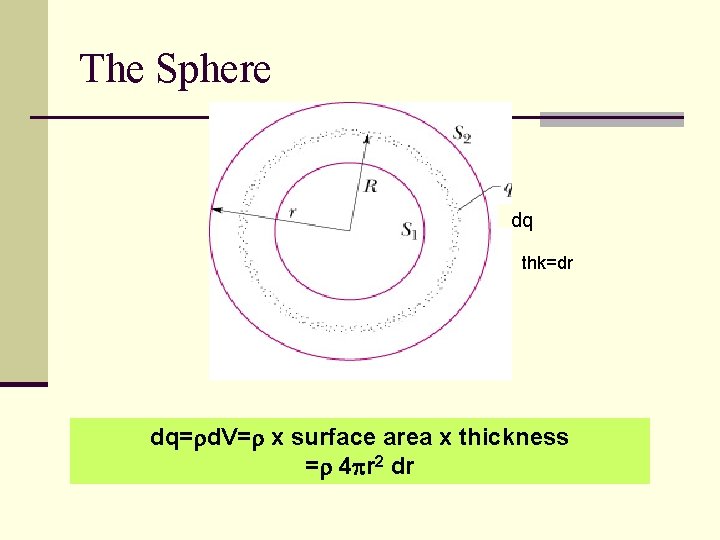
The Sphere dq thk=dr dq=rd. V=r x surface area x thickness =r 4 pr 2 dr

Summary (Note: I left off the unit vectors in the last equation set, but be aware that they should be there. )

To be remembered … n If the ELECTRIC FIELD at a point is E, then n E=F/q (This is the definition!) n Using some advanced mathematics we can derive from this equation, the fact that: