Electric currents Electromagnetism Microworld Macroworld Lecture 9 Electric















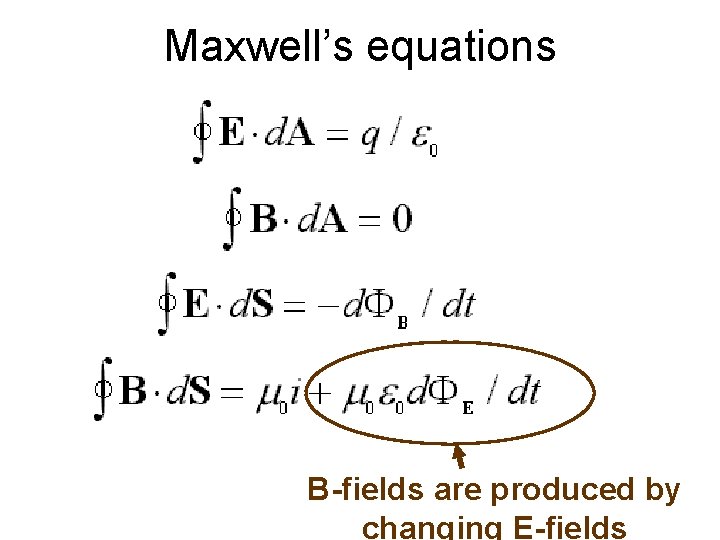





- Slides: 67

Electric currents & Electromagnetism Micro-world Macro-world Lecture 9

Electric currents (M oti on of ele c tri cc ha rge s) Micro-world Macro-world Lecture 9

Alessandro Volta

Positive Ions Atoms with one or more electrons removed _ _ _ + ++ ++ _ ”net” charge = +2 qe _ _

Battery C ++ -- + ++ + Zn Zn++ Zn - - Zn++ Zn Zn++ acid Zn Zn -Zn -

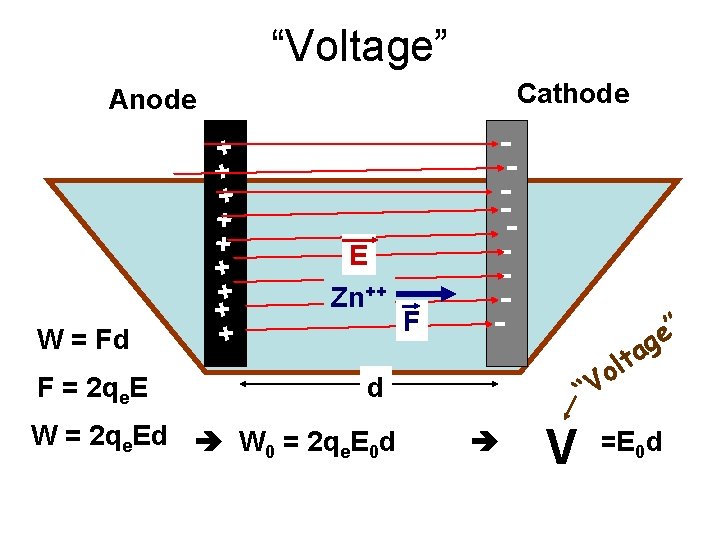
“Voltage” Cathode Anode F = 2 qe. E + + + ++ + W = Fd E Zn++ F -- ” e g “V d W = 2 qe. Ed W 0 = 2 qe. E 0 d a t l o W 0 =E 0 d 2 qe V

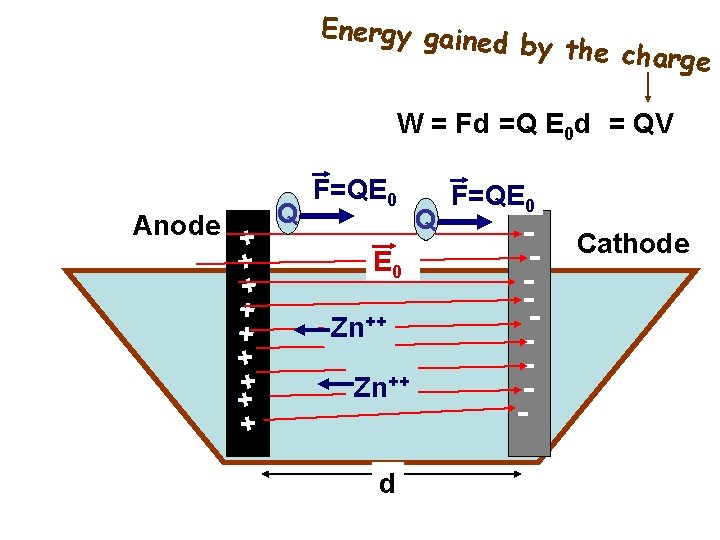
Energy gaine d by the cha rge W = Fd =Q E 0 d = QV Q + + + ++ + Anode F=QE 0 Zn++ d Q F=QE 0 -- Cathode

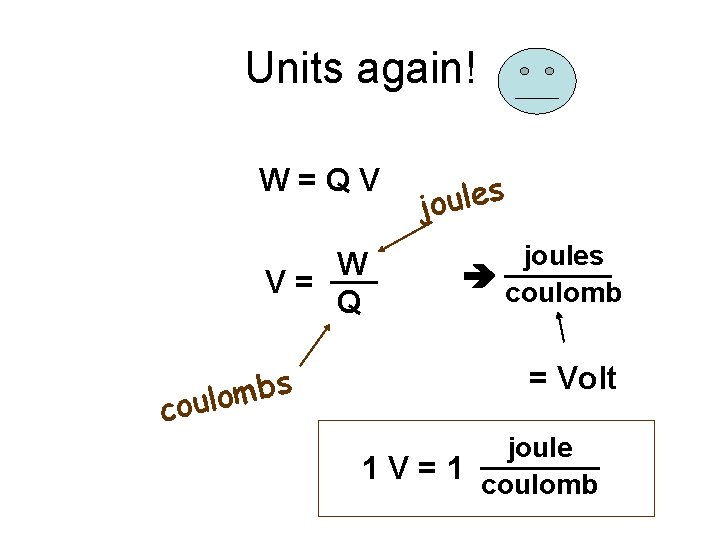
Units again! W=QV W V= Q s b m coulo s e l u o j joules coulomb = Volt joule 1 V = 1 coulomb

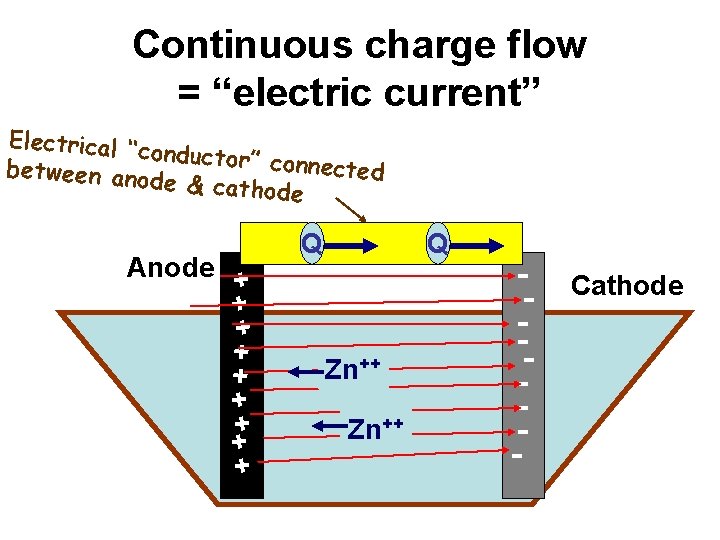
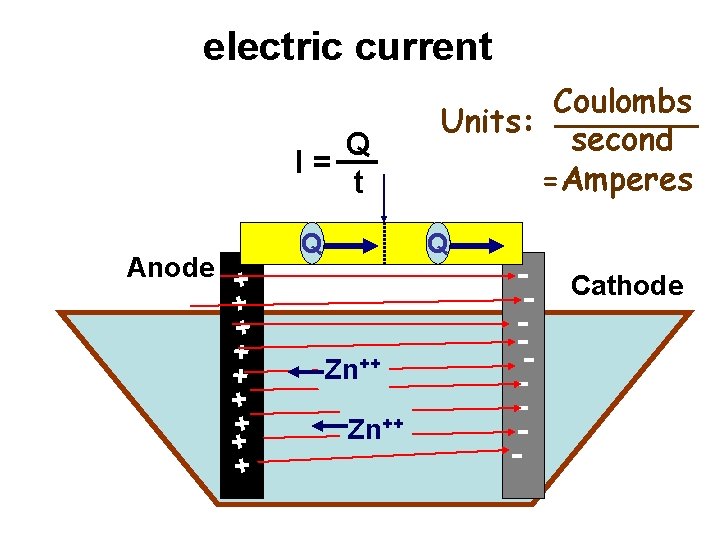
Continuous charge flow = “electric current” Electrical “c onductor” co nnected between ano de & cathod e + + + ++ + Anode Q Q Zn++ -- Cathode

electric current Q I= t + + + ++ + Anode Q Coulombs Units: second =Amperes Q Zn++ -- Cathode

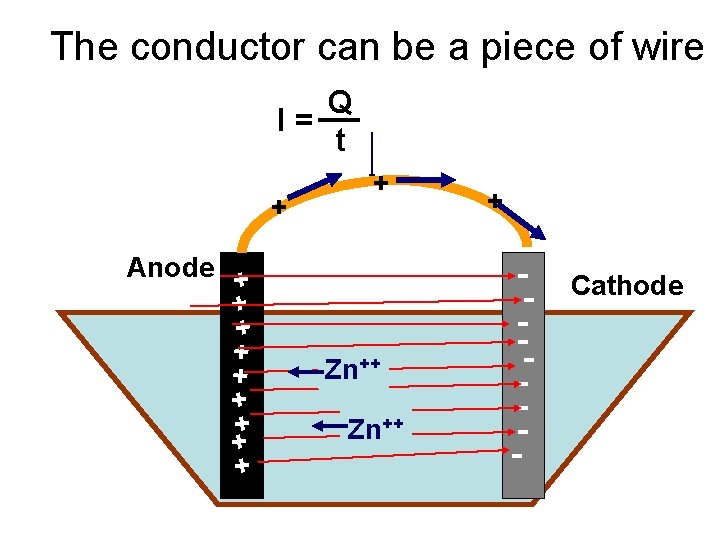
The conductor can be a piece of wire Q I= t + + + ++ + Anode + Zn++ + -- Cathode

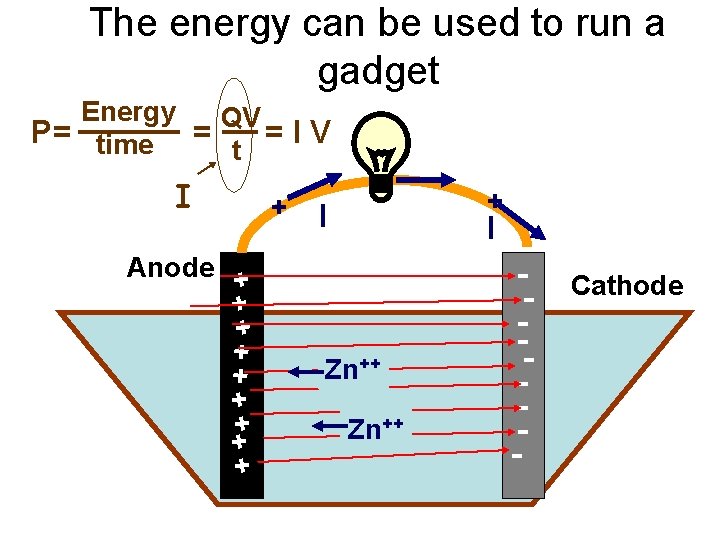
The energy can be used to run a gadget Energy QV P= time = =IV t I + + + ++ + Anode + I + + I Zn++ -- Cathode

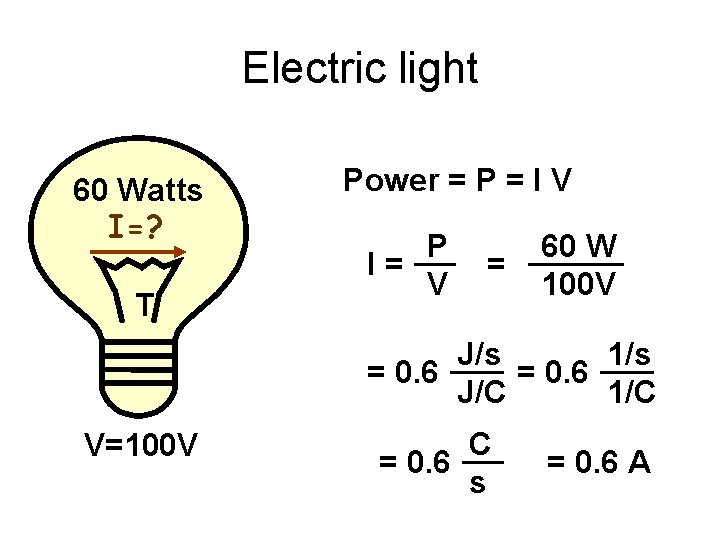
Electric light 60 Watts I=? T Power = P = I V P I= V = 60 W 100 V J/s 1/s = 0. 6 J/C 1/C V=100 V C = 0. 6 s = 0. 6 A

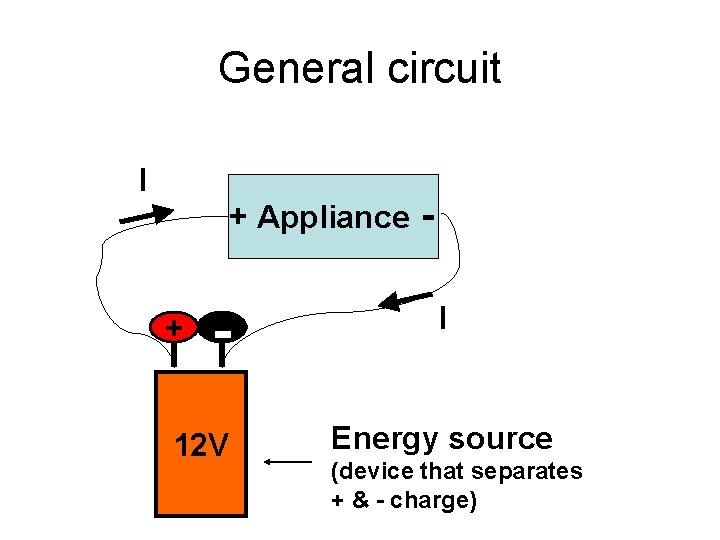
General circuit I + Appliance + - 12 V I Energy source (device that separates + & - charge)

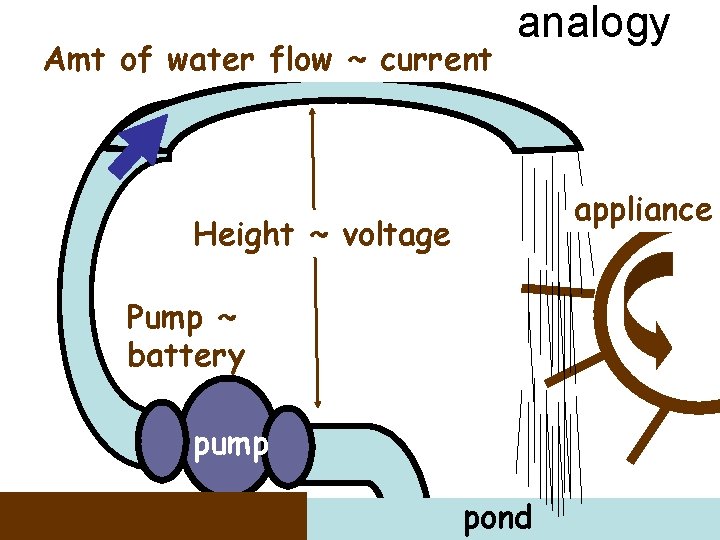
Amt of water flow ~ current analogy appliance Height ~ voltage Pump ~ battery pump pond

Voltas’ 1 st batteries

Christian Oersted

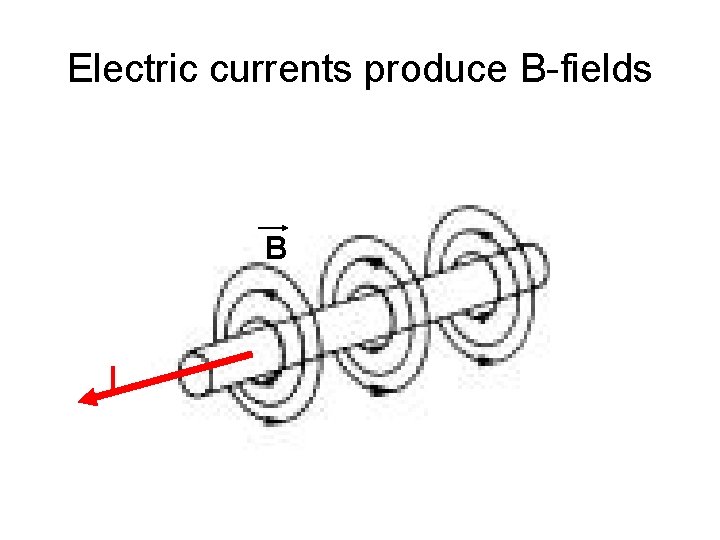
Electric currents produce B-fields B I

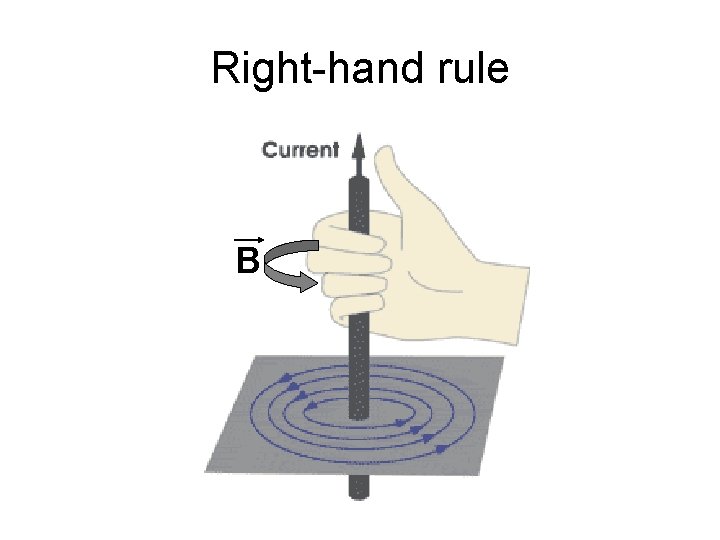
Right-hand rule B

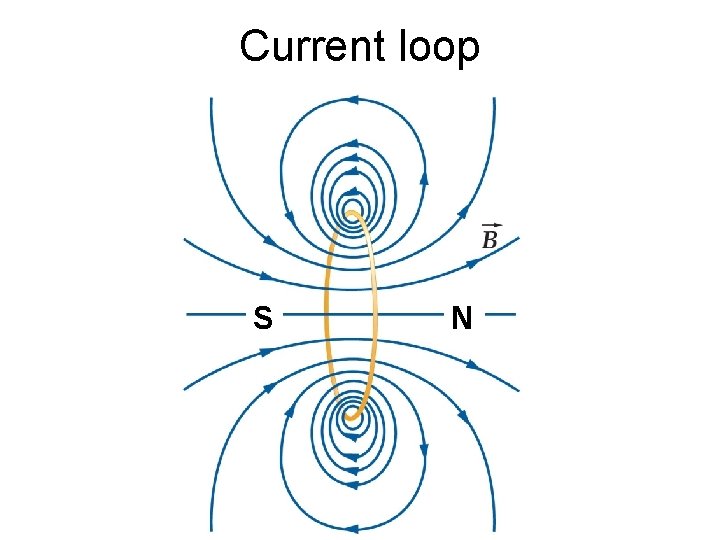
Current loop S N

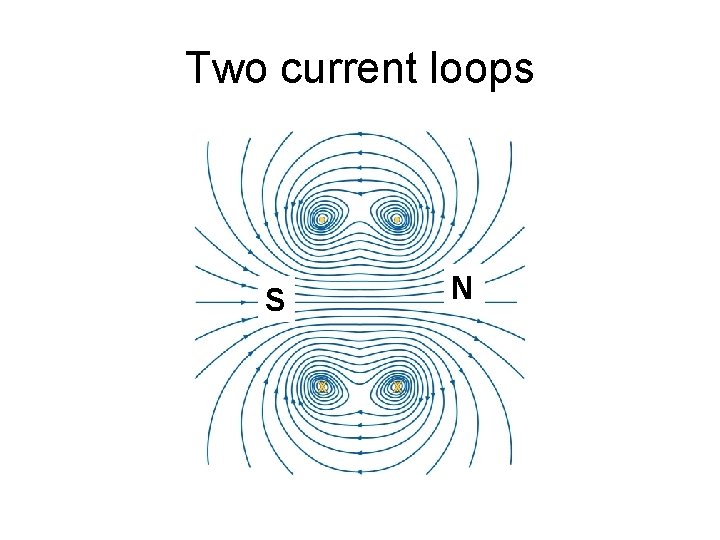
Two current loops S N

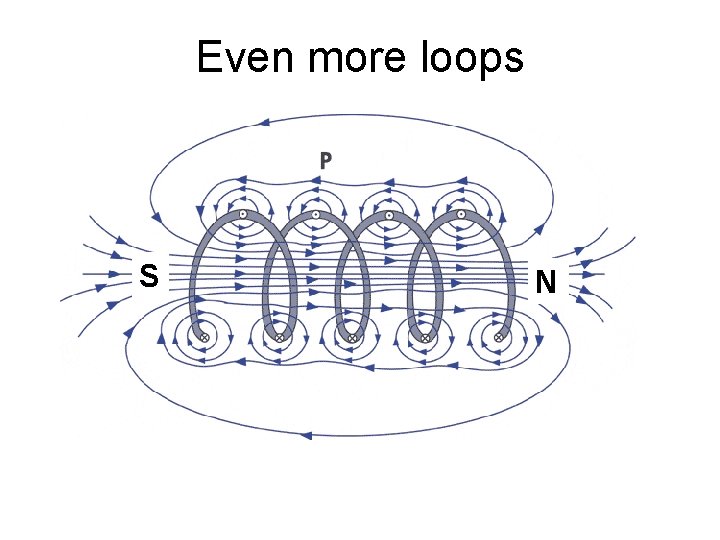
Even more loops S N

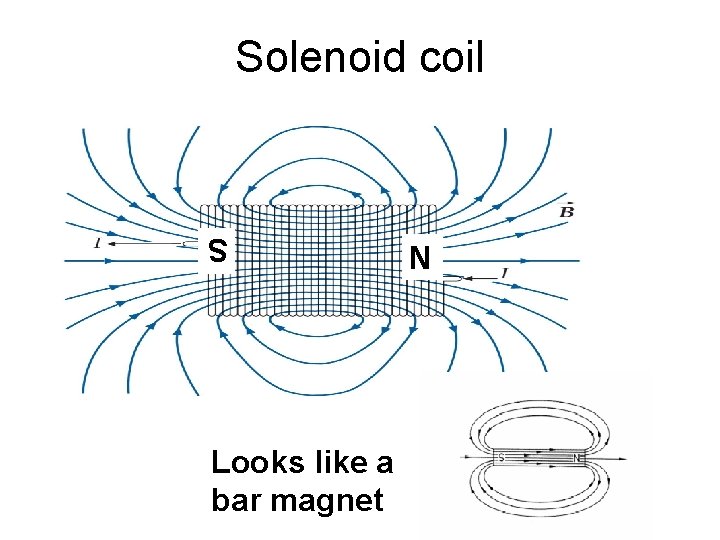
Solenoid coil S Looks like a bar magnet N

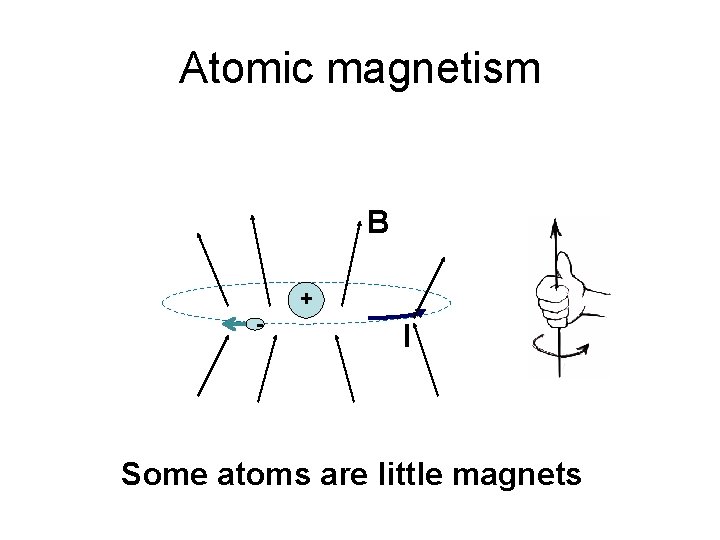
Atomic magnetism B + - I Some atoms are little magnets

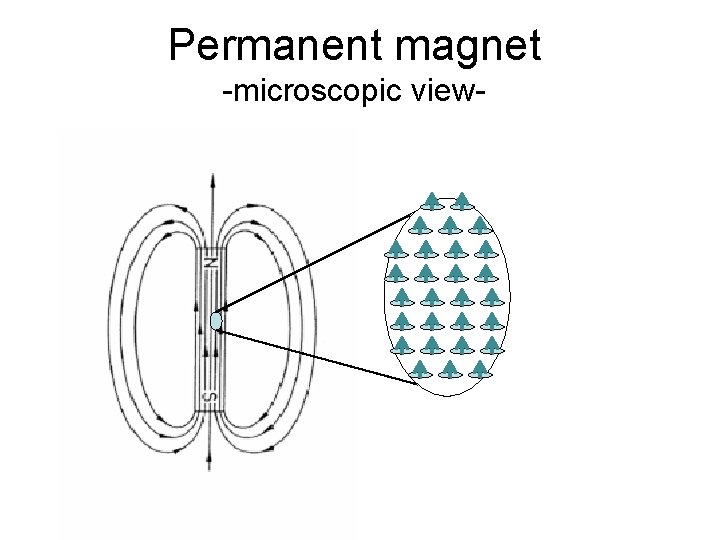
Permanent magnet -microscopic view-

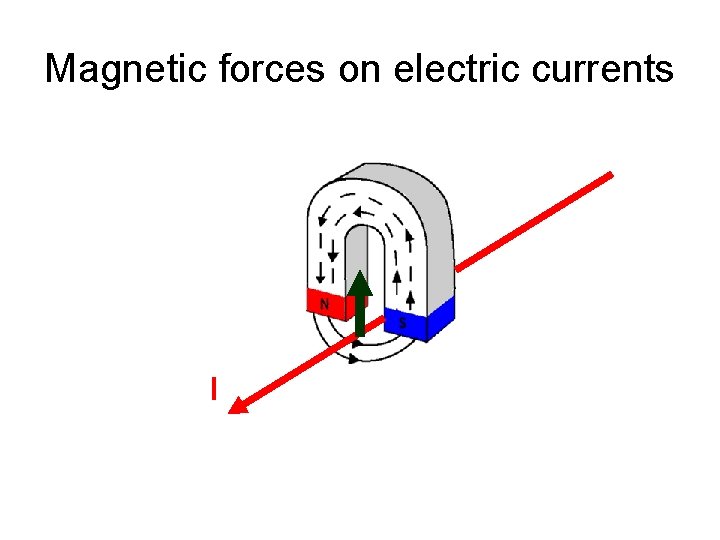
Magnetic forces on electric currents I

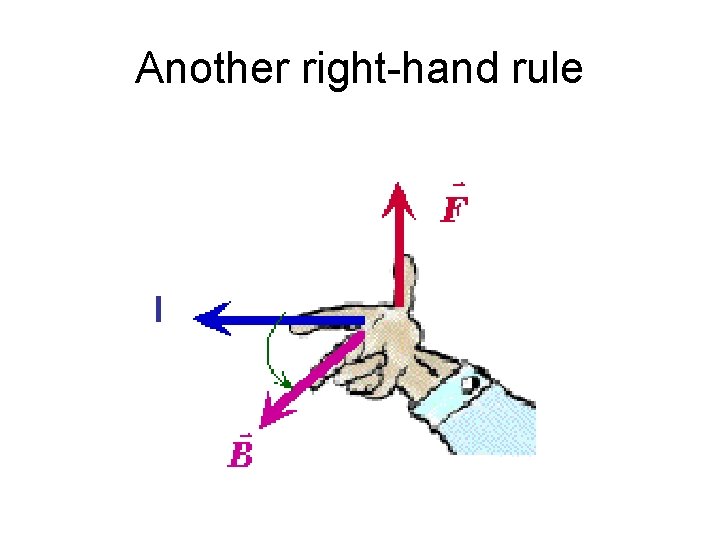
Another right-hand rule I

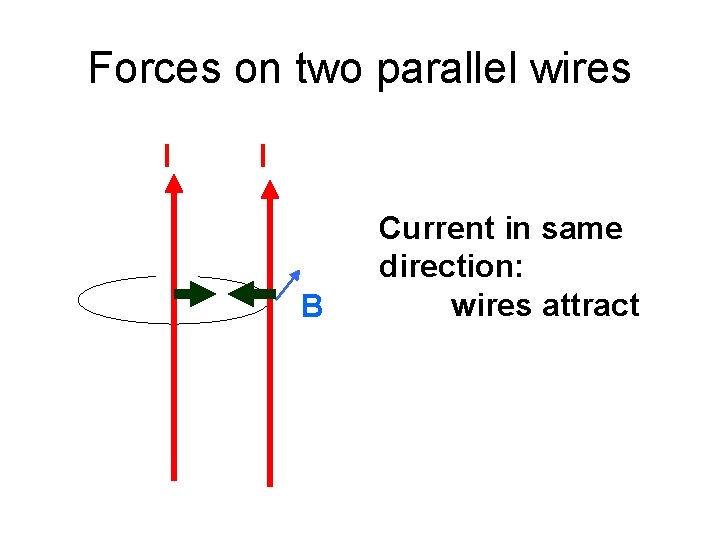
Forces on two parallel wires I I B Current in same direction: wires attract

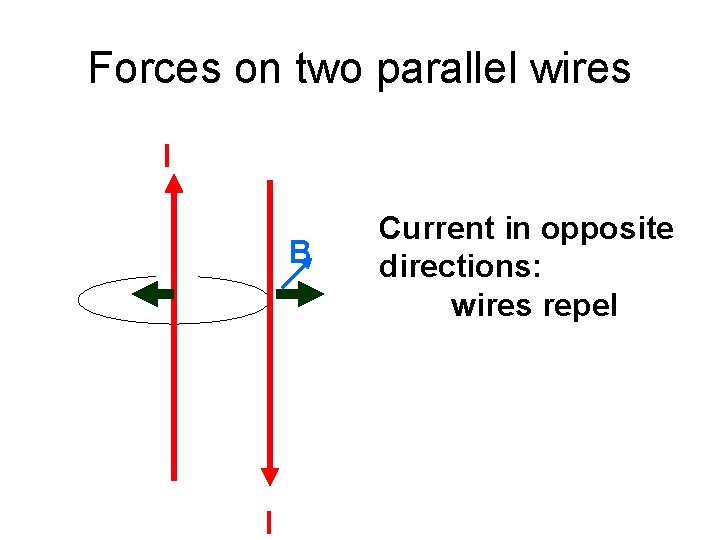
Forces on two parallel wires I B I Current in opposite directions: wires repel

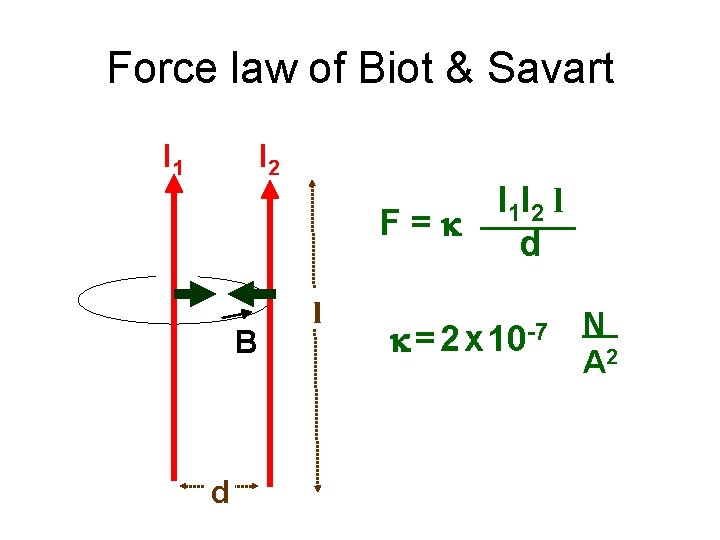
Force law of Biot & Savart I 1 I 2 I 1 I 2 l F=k d B d l k = 2 x 10 -7 N A 2

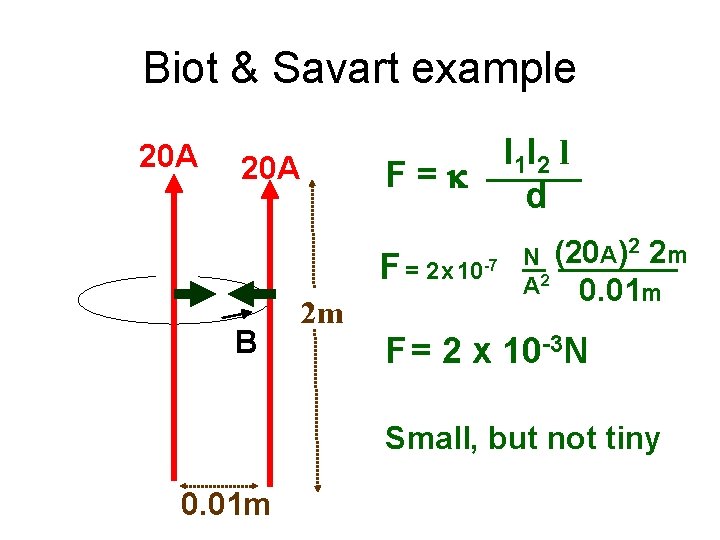
Biot & Savart example 20 A I 1 I 2 l F=k d 20 A F = 2 x 10 -7 B 2 m N (20 A)2 2 m A 2 0. 01 m F = 2 x 10 -3 N Small, but not tiny 0. 01 m

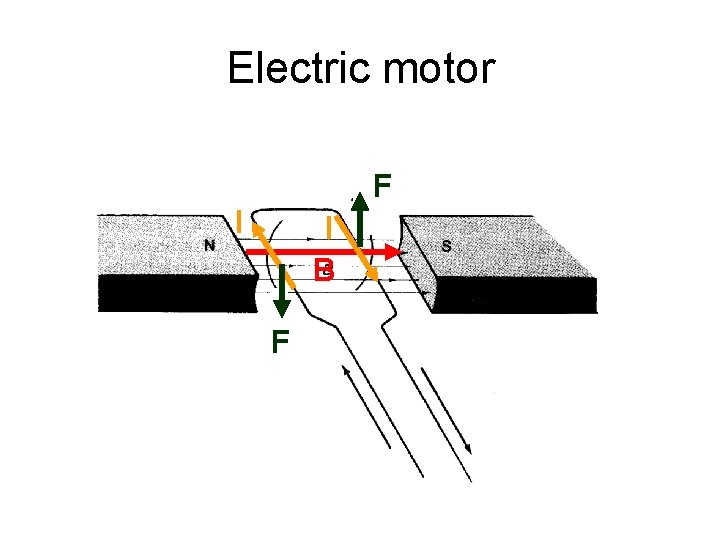
Electric motor F I I B F

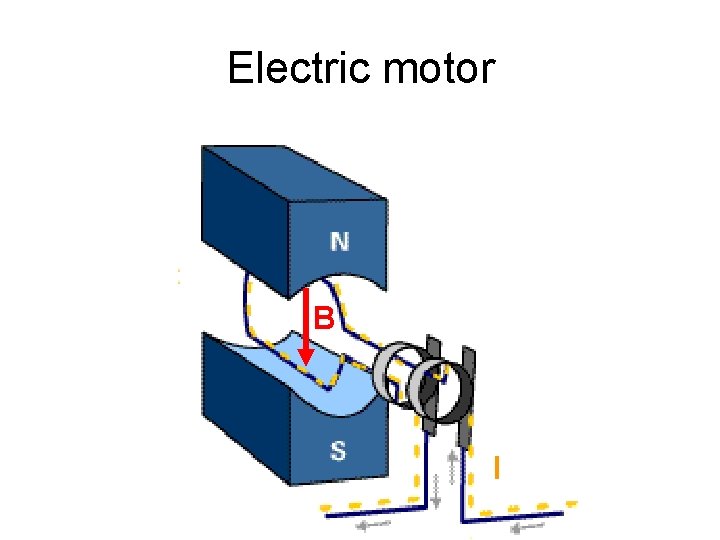
Electric motor B I

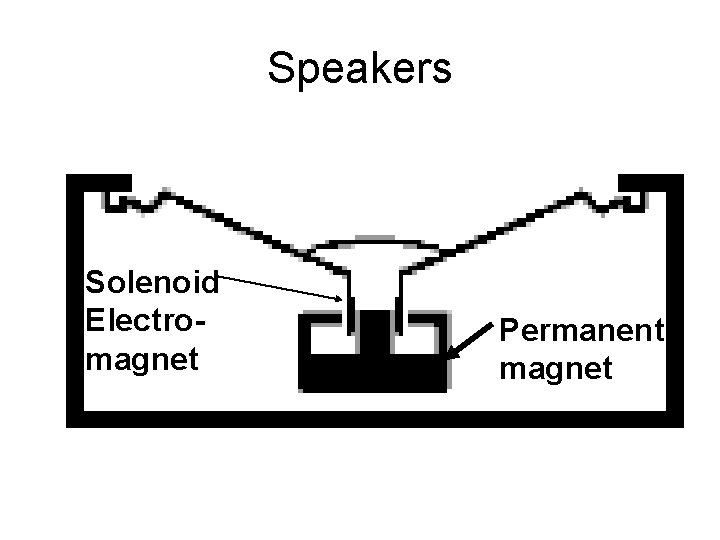
Speakers Solenoid Electromagnet Permanent magnet

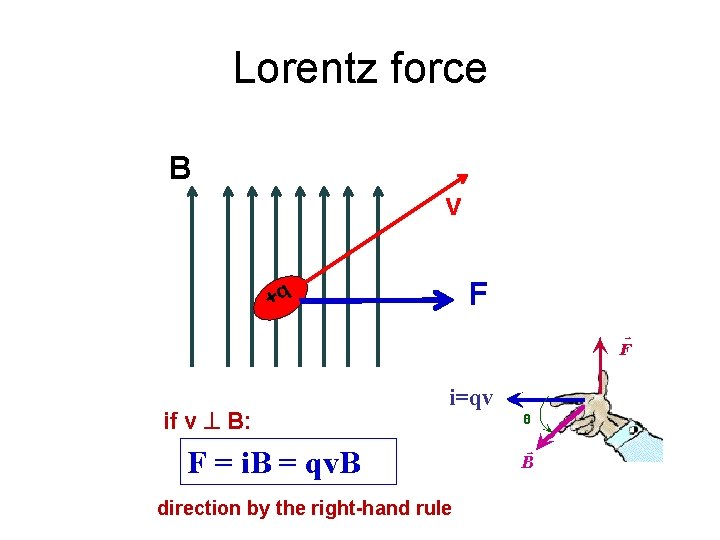
Lorentz force B v F +q if v B: i=qv F = i. B = qv. B direction by the right-hand rule

Electromagnetism Michael Faraday’s Law

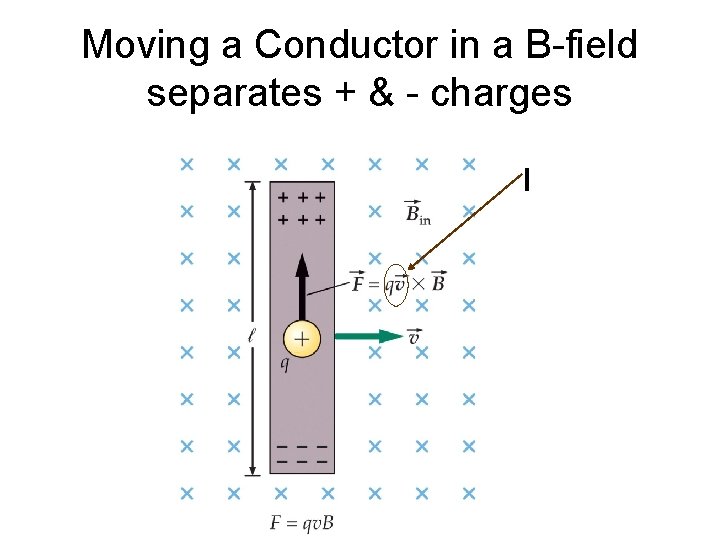
Moving a Conductor in a B-field separates + & - charges I

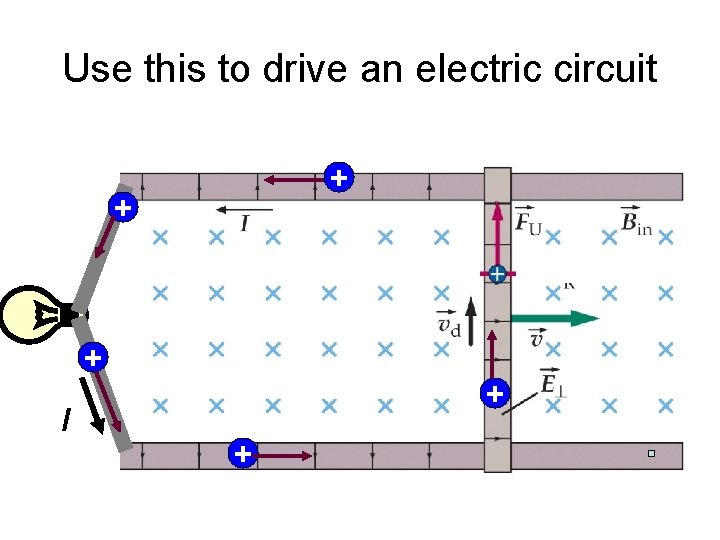
Use this to drive an electric circuit + + + I + +

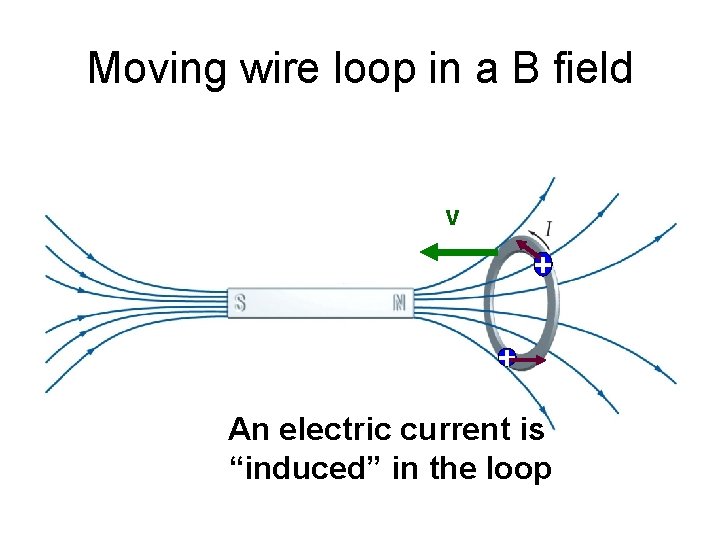
Moving wire loop in a B field v + + An electric current is “induced” in the loop

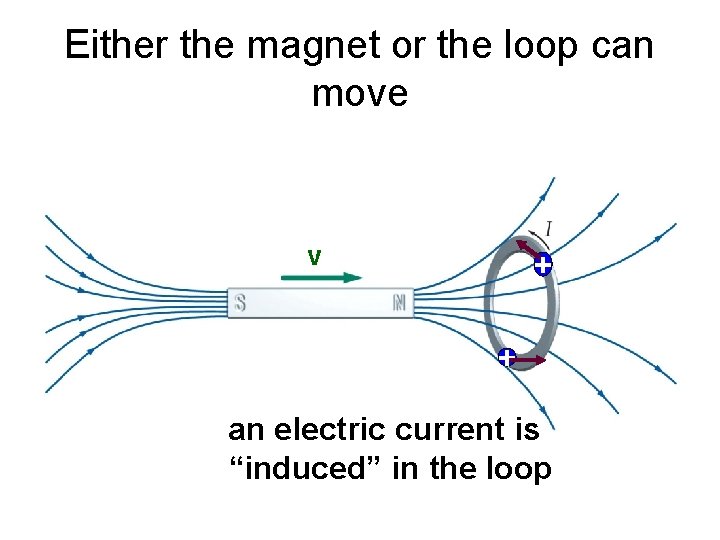
Either the magnet or the loop can move v + + an electric current is “induced” in the loop

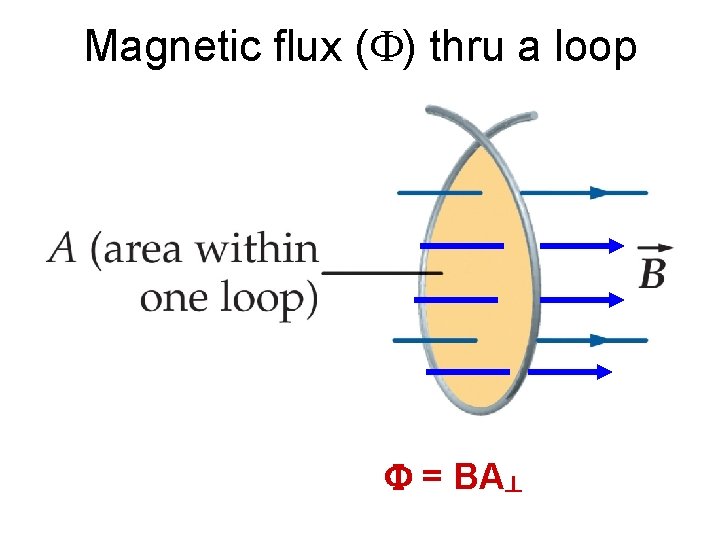
Magnetic flux (F) thru a loop F = BA┴

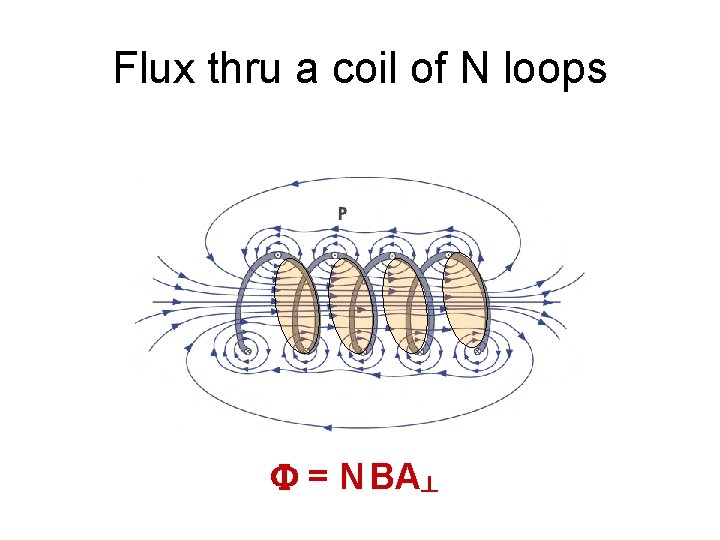
Flux thru a coil of N loops F = N BA┴

Faraday’s law Michael Faraday Induced voltage in a circuit = EMF = change in F elapsed time change in N BA┴ elapsed time “Electro-Motive Force”

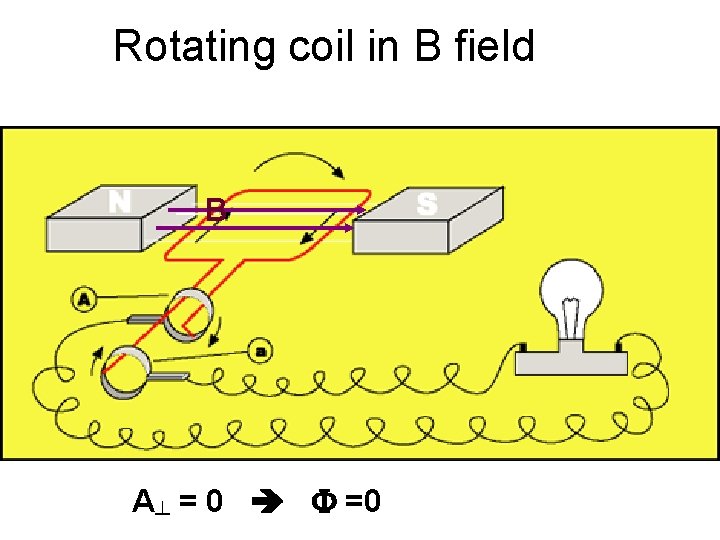
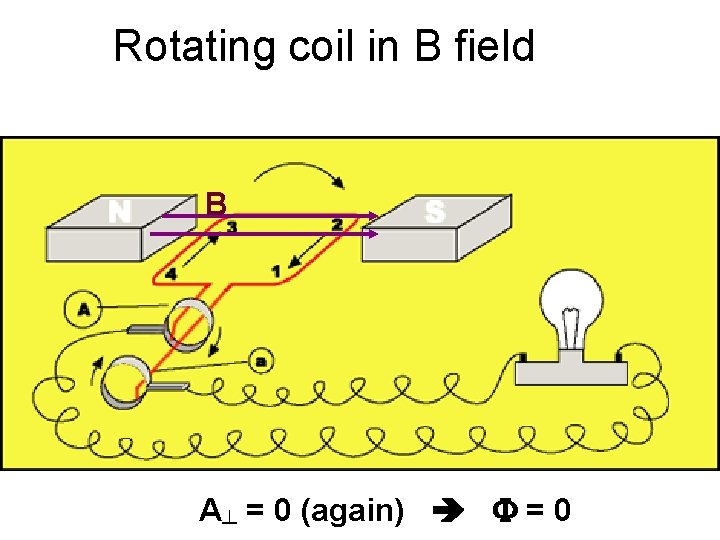
Rotating coil in B field B A┴ = 0 F =0

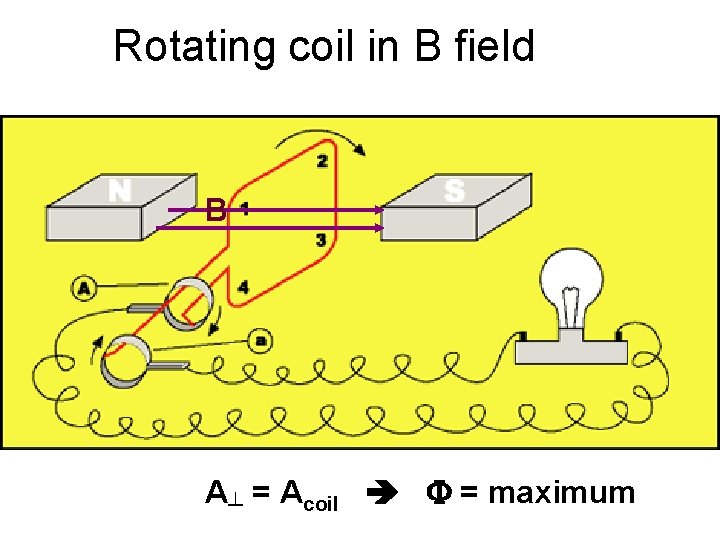
Rotating coil in B field B A┴ = Acoil F = maximum

Rotating coil in B field B A┴ = 0 (again) F = 0

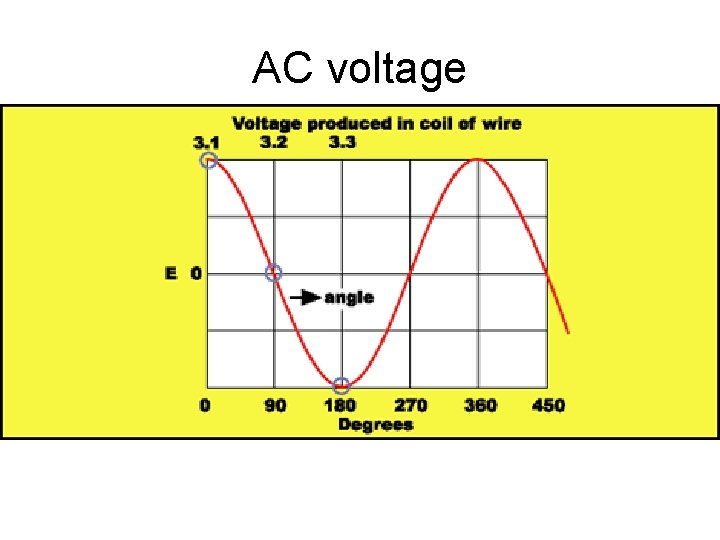
AC voltage

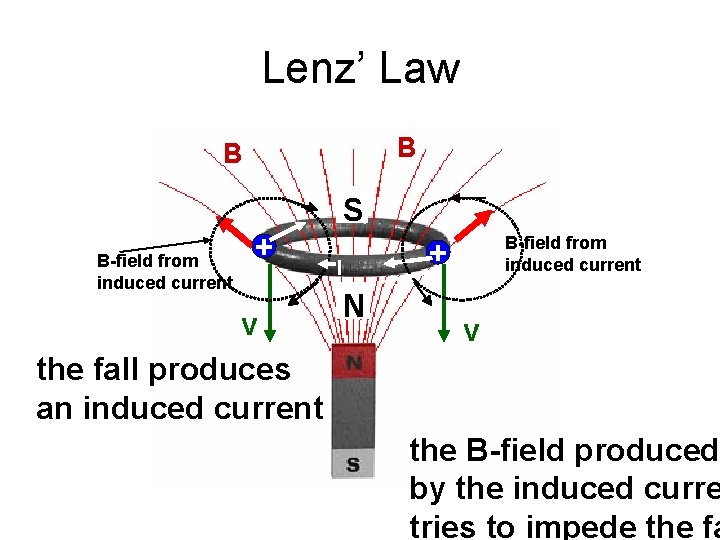
Lenz’ Law B B S B-field from induced current + v the fall produces an induced current B-field from induced current + I N v the B-field produced by the induced curre tries to impede the fa

Lenz’ law An induced voltage always gives rise to an electric current that creates a magnetic field that opposes the influence that produced it.

Maglev trains

Maglev

Maxwell’s Equations James Clerk Maxwell “…and then there was light. ”

Properties of E & B fields • Coulomb’s law: E-field lines start on + charge & end on – charge • Ampere’s law: B-fields are produced by electric currents • Faraday’s law: Changing B-fields produce E-fields • (un-named law): B-field lines never end

In equation form: E-field lines start on +charges & end on - charges B-field lines never end E-fields are produced by changing B fields B-fields are produced by electric currents

Maxwell The previous equations, as written, are mathematically inconsistent with the conservation of electric charge. He found he could fix this by adding one more term: B-fields are produced by changing E-fields
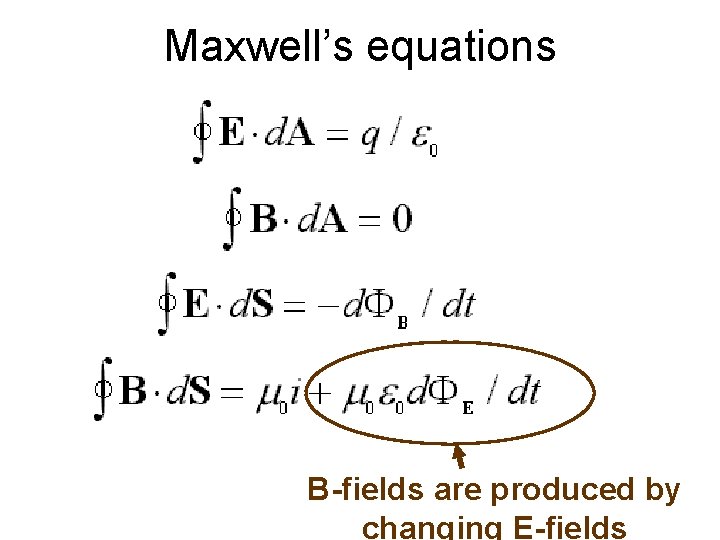
Maxwell’s equations B-fields are produced by changing E-fields

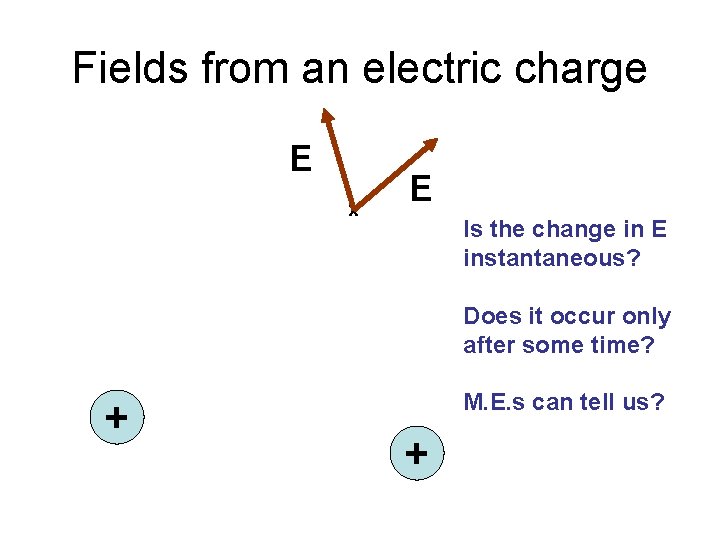
Fields from an electric charge E x E Is the change in E instantaneous? Does it occur only after some time? + M. E. s can tell us? +

fun in the bathtub Water level will increase but not instantaneously 1 st waves will propagate from her entrance point to the edge of the tub

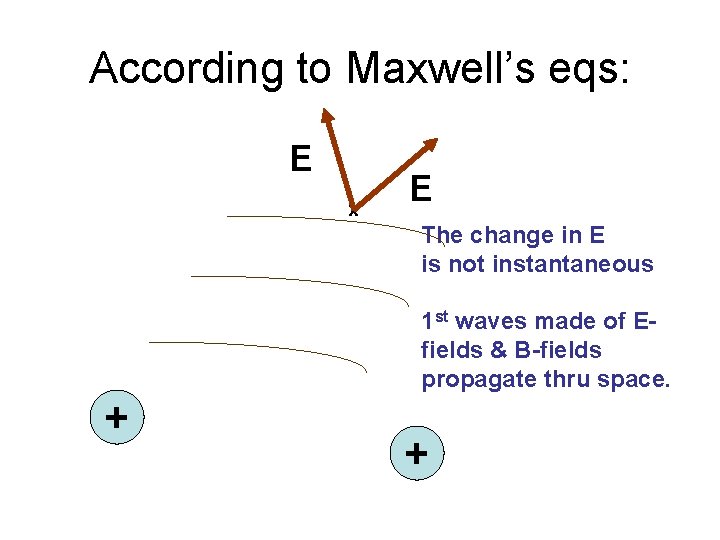
According to Maxwell’s eqs: E x E The change in E is not instantaneous 1 st waves made of Efields & B-fields propagate thru space. + +

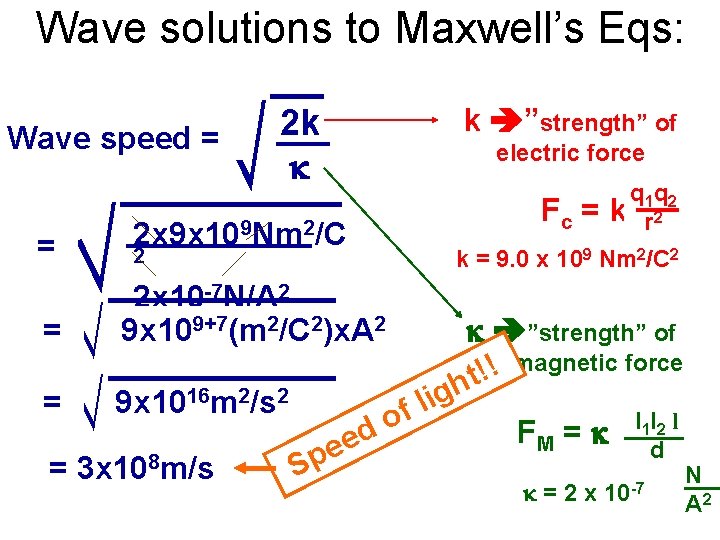
Wave solutions to Maxwell’s Eqs: Wave speed = = = electric force k = 9. 0 x 109 Nm 2/C 2 2 x 10 -7 N/A 2 9 x 109+7(m 2/C 2)x. A 2 3 x 108 m/s k ”strength” of magnetic force ! ! ht g i l f 16 m 2/s 2 e p S q 1 q 2 k r 2 Fc = 2 x 9 x 109 Nm 2/C 2 = 9 x 10 = k ”strength” of 2 k k o d e FM = k k=2 x I 1 I 2 l d 10 -7 N A 2

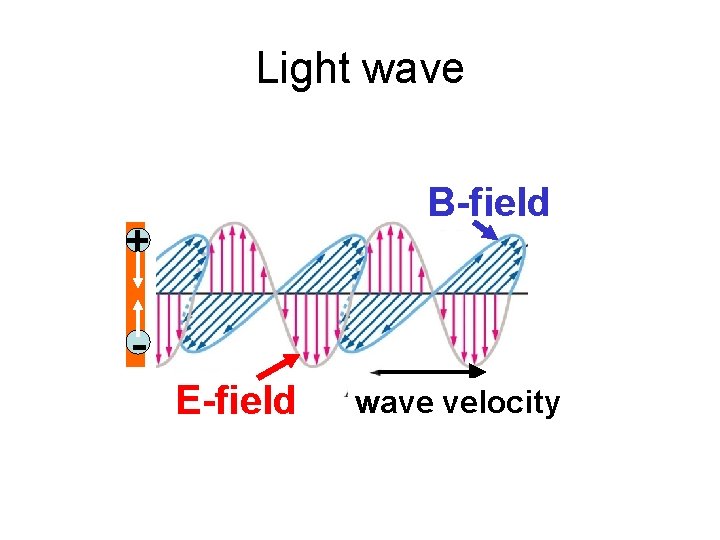
“…let there be light. ” Maxwell’s equations have solutions that are waves of oscillating E- & B-fields that travel at the speed of light. Faraday & Maxwell made the immediate (& correct) inference that these waves are, in fact, light waves.

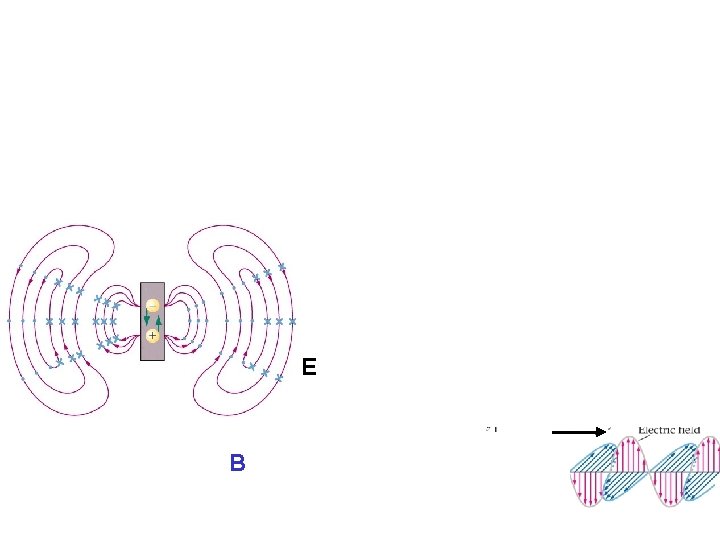
EM waves + + + -

antenna E B

antenna E B

Light wave B-field + E-field wave velocity

Light wave animation E B

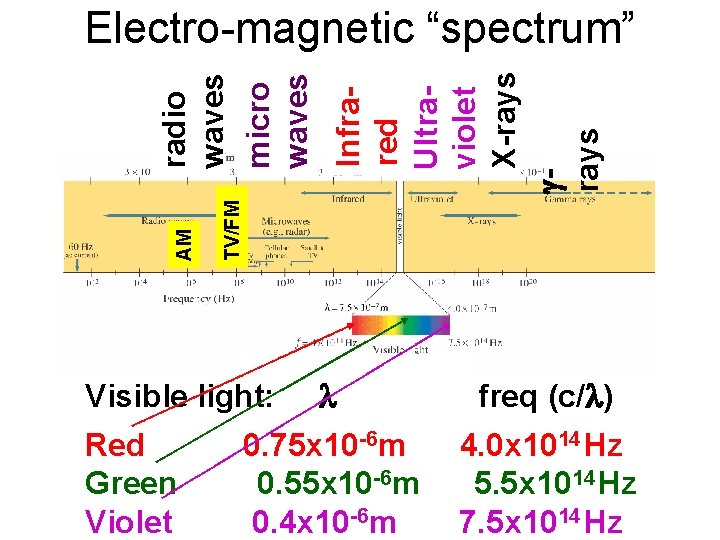
l freq (c/l) 0. 75 x 10 -6 m 0. 55 x 10 -6 m 0. 4 x 10 -6 m 4. 0 x 1014 Hz 5. 5 x 1014 Hz 7. 5 x 1014 Hz Visible light: Red Green Violet Infrared Ultraviolet X-rays grays TV/FM AM radio waves micro waves Electro-magnetic “spectrum”