Electric Current Electricity Lesson 1 Learning Objectives n

Electric Current Electricity Lesson 1

Learning Objectives n To establish what you already understand about electricity. n To know what is meant by an electric current. n To know how to calculate the charge flow in a circuit.

The Plan. . . n To check what you remember from GCSE. n Build some circuits to check/change your ideas. n Discuss what is meant by electric current. n Practice some calculations.

Electricity Random Fact n Electrons only move through a wire at a speed of about 1 mm/sec.

Electric Current n n The electric current is the rate of flow of charge in a wire or component. unit is the ampere (A) n Due to the passage of charge particles referred to as charge carriers. n In metals the charge carriers are electrons.

The Coulomb n The unit of charge is the coulomb (C), which is defined as the charge flow in one second when the current is one ampere. n n The symbol for charge is Q. The symbol for the unit, coulomb is C. n The charge on an electron is e=1. 6 × 10 -19

Charge Flow n For a current I, the charge flow ΔQ in a time Δt is given by: - n The symbol Δ is delta, a Greek capital letter Δ, meaning “change in”.

Current n For a current I, the charge flow ΔQ in a time Δt is given by: -

Question n If the charge on one electron is e=1. 6 × 1019 C, how many electrons are needed to make up 1 C of charge?

Answer n If the charge on one electron is e=1. 6 × 1019 C, how many electrons are needed to make up 1 C of charge?

Possible Trap n There are some important multipliers for current: n 1 microamp (1 μA) = 1 × 10 -6 A 1 milliamp (1 m. A) = 1 × 10 -3 A n n You must use current in amps, charge in coulombs and time in seconds for calculations.

Worked Example n What is the charge passing a point if a current of 10 p. A flows for 1 year?

Learning Objectives n To establish what you already understand about electricity. n To know what is meant by an electric current. n To know how to calculate the charge flow in a circuit.

End

Calculating the number of electrons n Knowing that the charge on an electron is – 1. 6 ´ 10– 19 C, you can calculate the number of electrons in a 'spoonful' of charge. A typical spoonful of negative charge is – 2 n. C. So the number of electrons is:

Discussion: Defining current, the coulomb n n n Current is defined as rate of change of charge. This can be done graphically. Current is the gradient of a graph of charge transferred against time. I = d. Q/dt. The idea of the gradient can be introduced by asking how the charge transferred by the shuttling ball increases with time - it will go up in a series of steps but, given a large number of transfers, these will approximate to a constant slope. The average current is equal to its gradient. The equation I = Q/t (familiar from pre-16 science lessons) is useful but stress that this refers to an average current I and care must be taken when I is changing. A current of one amp is equivalent to a flow of one coulomb per second. The coulomb defined as the charge passed by a current of 1 A in 1 s, i. e. 1 C = 1 A s.

Introductory questions on charge and current n n n n n Convert 25 m. A to A 2. Convert 0. 50 A to m. A 3. A torch bulb passes a current of 120 m. A. (a) How many coulombs of charge flow through the lamp in 1 minute? (b) How many coulombs of charge flow through the lamp in 1 hour? (c) How many electrons leave the negative terminal of the cell each second? 4. A car battery is rated as 36 A h. In principle this means it could pass a current of 1 A for 36 h before it runs down. How much charge passes through the battery if it is completely run down? 5. An electron beam in a beam tube carries a current of 125 A. (a) What charge is delivered to the screen of the tube every second?

Circuit rules Current rules n At any junction in a circuit the total current leaving the junction is equal to the total current entering the junction (Kirchhoff’s current Law) n The current entering a component is the same as the current leaving the component (from KS 3 and 4) n The current passing through 2 or more components in series is the same through each component. (from KS 3 and 4)

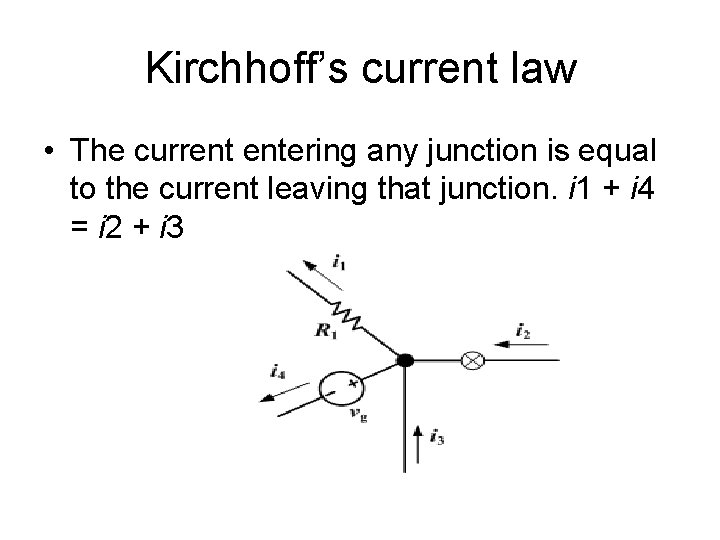
Kirchhoff’s current law • The current entering any junction is equal to the current leaving that junction. i 1 + i 4 = i 2 + i 3

Conclusions n n The current is the charge per second : I = d. Q/dt. At any junction in a circuit the total current leaving the junction is equal to the total current entering the junction (Kirchhoff’s current Law) The current entering a component is the same as the current leaving the component The current passing through 2 or more components in series is the same through each component.