Electric Current chapters 22 23 Electric Current n

Electric Current chapters 22 23

Electric Current n n Whenever electric charges of like signs move, an electric current is said to exist The current is the rate at which the charge flows through this surface n n Look at the charges flowing perpendicularly to a surface of area A The SI unit of current is Ampere (A) n 1 A = 1 coulomb/sec

What makes the charge flow? n n …. a potential difference in energy levels …. similar to n n the way heat flows from hot surface to cold surface The way objects fall from location of high PE to location of low PE

n Potential difference charge flows when there is a difference in voltage across the ends of a conductor

Electric Current, cont n The direction of the current is the direction positive charge would flow n This is known as conventional current direction n In a common conductor, such as copper, the current is due to the motion of the negatively charged electrons Technically, negative charges leave the (-) end of the battery and return to the (+) end BUT the current is said to flow the opposite way : (+) to (-) Blame Ben Franklin for this definition for the direction

More about current n n Ex: 5 amps = movement of 5 coulombs of charge in one second or about 31. 25 billion electrons each second. The net charge of any wire is zero because just as many electrons leave the wire that enter it.

Charges form a conga line. . n n n Everything already contains electrons so… A circuit doesn’t provide electrons but. . It does provide all the requirements for charges to get energized and start moving and doing work

Sources of potential difference n n A voltage source provides a sustained potential difference to allow charges to flow. Examples: dry cells, wet cells, i. e. batteries, and generators/powerplants Dry cells and wet cells are the result of a chemical reaction. Generators/powerplants convert mechanical energy to electrical energy.

Voltage n n n This is like the electric pressure pushing the electrons. Example: The potential difference between two slots in a household outlet is ~120 volts or 120 joules/coulomb of charge. Voltage is the potential energy /unit of charge that pushes the electrons.

Analogy for electricity n n n n Charges…. water molecules Electric current…flow of water current Voltage source…pump Voltage…pressure Wires…pipes Do work of lighting a bulb…do work of turning a water wheel to grind grain Resistance to electricity…rocks, gunk in pipes

Resistance n n In a conductor, the voltage applied across the ends of the conductor is proportional to the current through the conductor The constant of proportionality is the resistance of the conductor

Resistance, cont n Units of resistance are ohms (Ω) n n n 1 Ω = 1 V / A Resistance in a circuit arises due to collisions between the electrons carrying the current with the fixed atoms inside the conductor Mostly depends on material, thickness and length of wire

n Electric resistance can slow down the flow of electrons. n Thick wires have less resistance. n Short wires have less resistance.

Ohm’s Law n n Experiments show that for many materials, including most metals, the resistance remains constant over a wide range of applied voltages or currents This statement has become known as Ohm’s Law n n ΔV = I R Ohm’s Law is an empirical relationship that is valid only for certain materials n Materials that obey Ohm’s Law are said to be ohmic

Units for Ohm’s law n n V = I R Voltage = current x resistance equatio n V= I R variable voltage current resistance unit volt ampere ohm Unit symbol v A Ω Basic units Joules/ coulomb Coulomb Not /sec applicable

Ohm’s Law and shock n Example of 1. 5 volt battery n Touching battery and exposed Christmas bulb wires in class produces no shock or sensation at all n n Resistance of dry hands was very high, resulting current very low If you touched battery and wires with wet hands… n n Might feel something sensation Resistance of wet hands is lower, resulting current is higher

Birds on exposed wire, no shock? ? n n IF the bird has one foot on our original wire, and the other foot on, for example, the ground or on a different wire with less voltage, THEN the bird would be electrocuted. The electricity would pass through the bird on its way from the high-voltage line to the lowervoltage line or the ground. BUT as long as both of the bird’s feet are on the same wire (or wires of the same voltage), the bird is safe. The current doesn’t have anywhere else to go, so the electricity won’t pass through the bird–it stays on the path of least resistance, the wire.

Person dangling from high tension wire? n n It’s like being part of a huge Vande. Graf machine! Don’t make contact with ‘ground’! Turn power off, then rescue… http: //www. dailymail. co. uk/news/article-2244478/Paraglider-tangled-high-powered-powerlines-man-dices-death-spending-hours-dangling-100 m-ground. html

Squirrels on the other hand… When one end of a squirrel touches ground or a transformer and the other end is still on an electrified wire……. n The circuit is complete! Surprising reason for some power outages! n

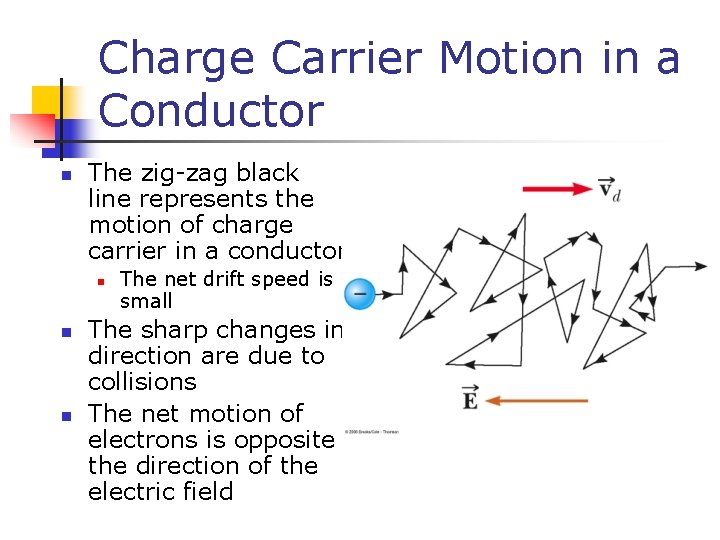
Charge Carrier Motion in a Conductor n The zig-zag black line represents the motion of charge carrier in a conductor n n n The net drift speed is small The sharp changes in direction are due to collisions The net motion of electrons is opposite the direction of the electric field

Electrons in a Circuit n n n The drift speed is much smaller than the average speed between collisions When a circuit is completed, the electric field travels with a speed close to the speed of light Although the drift speed is on the order of 10 -4 m/s the effect of the electric field is felt on the order of 108 m/s

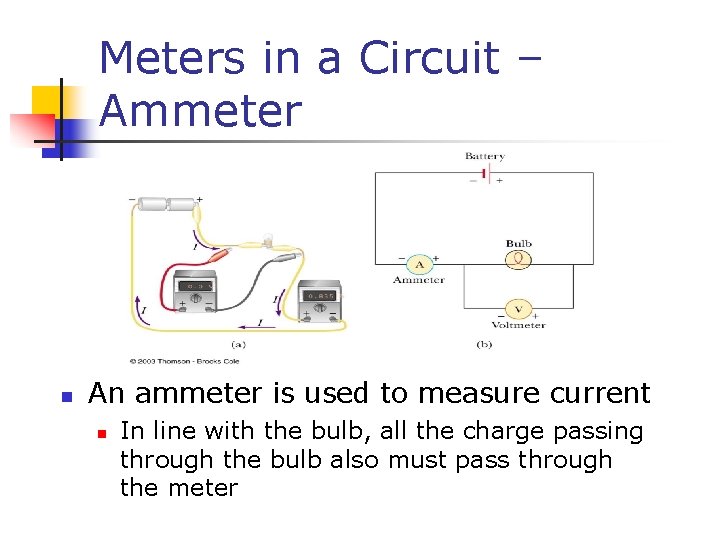
Meters in a Circuit – Ammeter n An ammeter is used to measure current n In line with the bulb, all the charge passing through the bulb also must pass through the meter

Meters in a Circuit – Voltmeter n A voltmeter is used to measure voltage (potential difference) n Connects to the two ends of the bulb

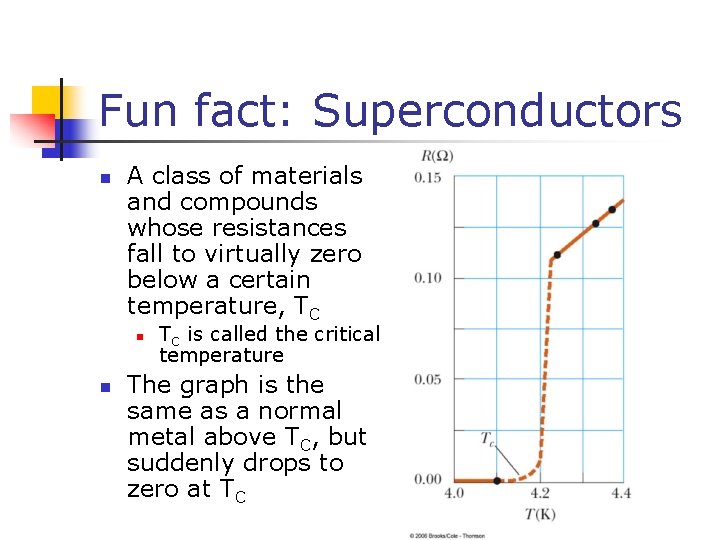
Fun fact: Superconductors n A class of materials and compounds whose resistances fall to virtually zero below a certain temperature, TC n n TC is called the critical temperature The graph is the same as a normal metal above TC, but suddenly drops to zero at TC

Superconductor, final n n Good conductors do not necessarily exhibit superconductivity One application is superconducting magnets

Electrical Energy and Power n In a circuit, as a charge moves through the battery, the electrical potential energy of the system is increased by ΔQΔV n n The chemical potential energy of the battery decreases by the same amount As the charge moves through a resistor, it loses this potential energy during collisions with atoms in the resistor n The temperature of the resistor will increase

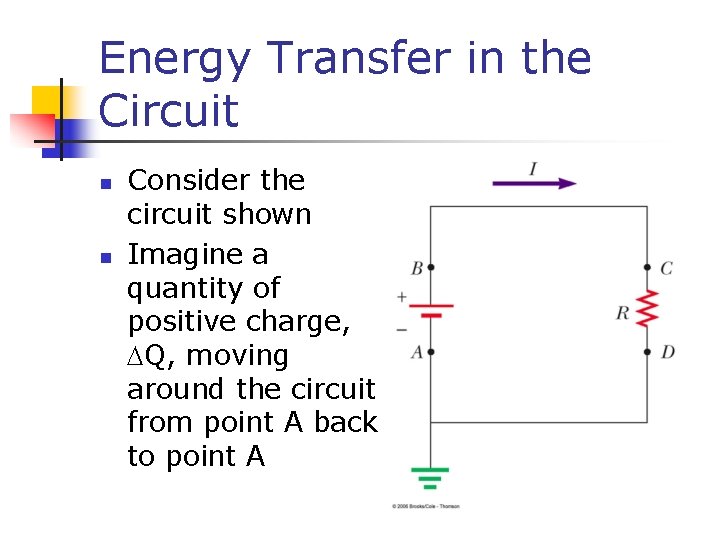
Energy Transfer in the Circuit n n Consider the circuit shown Imagine a quantity of positive charge, DQ, moving around the circuit from point A back to point A

Energy Transfer in the Circuit, cont n Point A is the reference point n n It is grounded and its potential is taken to be zero As the charge moves through the battery from A to B, the potential energy of the system increases by DQDV n The chemical energy of the battery decreases by the same amount

Energy Transfer in the Circuit, final n n n As the charge moves through the resistor, from C to D, it loses energy in collisions with the atoms of the resistor The energy is transferred to internal energy When the charge returns to A, the net result is that some chemical energy of the battery has been delivered to the resistor and caused its temperature to rise

Electrical Energy and Power, cont n n n The rate at which the energy is used is the power Electrical appliances are often described in terms of power required or watts Power determines the brightness of a lamp n More voltage, more current or both

What does the electric company sell? n n Electrons? No, all matter has that Electricity? Power? n n Be more specific Energy! n n Our units - Joules Their units – k. Whr n Kilowatt x hr

Electrical Energy and Power, final n The SI unit of power is Watt (W) n n Watt = joules/sec What’s a kilowatt-hour ? n n amount of energy used in one hour at a rate of 1 kilojoule/sec (1 k. W) 1 k. Wh = 3. 60 x 106 J

Using electrical energy n n Produced at power plant To your house converted to any variety of energies by appliances Ex: transfer to heat energy n n Toaster, iron, curling iron, heater 100 % efficient or not?

Calculate cost of operation n Ex: 1500 watt microwave oven n Estimate hours of operation/ day n n Determine rate charged by electric co per kwhr n n ~ 1. 5 hours (must be in hours!) From electric bill- $0. 18/k. Whr or 18 cents Cost = k. W x hrs x rate n n = (1500/1000) x (1. 5) x ($0. 18) = $0. 405 or about 41 cents per day

Chapter 35 n Electric Circuits

What makes a good circuit? n n n Must use all conductors Must include voltage source Complete path n n From (+) to (-) end of voltage source No short circuits No breaks, gaps All electrical devices working

What is a circuit? n Path along which the charges flow Electrical devices, voltage sources, wiring can be connected in a variety of ways • Series – single loop or path • Parallel – circuit has branches

Observations about Series circuits n n Same current throughout the single loop Voltage at battery = sum of voltage drops across the bulbs = V 1 +V 2, etc n n Add more bulbs, bulbs get dimmer, less power One bulb is unscrewed, all bulbs go out – disadvantage total resistance increases as more bulbs are added to the circuit n R total = R 1 + R 2 + etc. Advantage – uses less power, batteries last longer

Observations about parallel circuits n Same voltage throughout the circuit n n Current at the battery=sum of currents in all branches n n Voltage at battery = v 1 = v 2 = etc. I total = I 1 + I 2 + etc. One bulb unscrewed, rest stay on – advantage Add more bulbs, total resistance decreases Add more bulbs, total current increases n Disadvantage – can overload the circuit causing overheating of wires n Can protect the circuit by including circuit breaker or fuse in the main branch

Resistors/resistances in circuits n In series n n n Total or equivalent R = R 1 +R 2 + etc total increases with more resistors In parallel n Total or equivalent R n n 1 / R total = 1/R 1 + 1/R 2 + etc. Total decreases with more resistors

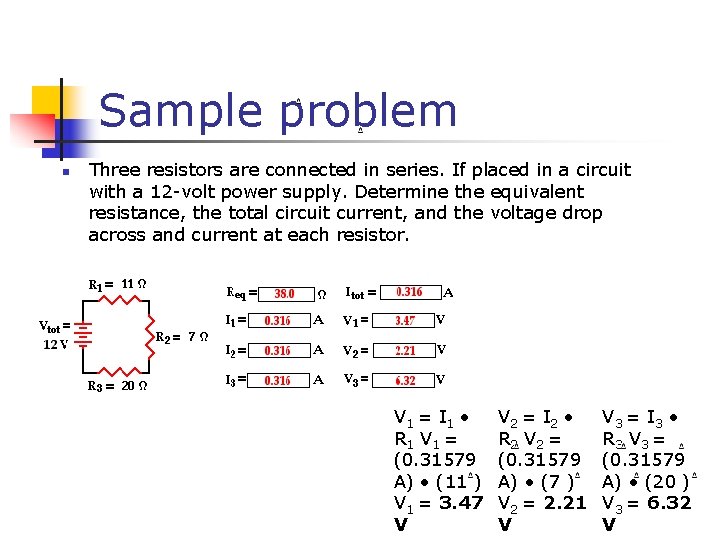
Sample problem n Three resistors are connected in series. If placed in a circuit with a 12 -volt power supply. Determine the equivalent resistance, the total circuit current, and the voltage drop across and current at each resistor. V 1 = I 1 • R 1 V 1 = (0. 31579 A) • (11 ) V 1 = 3. 47 V V 2 = I 2 • R 2 V 2 = (0. 31579 A) • (7 ) V 2 = 2. 21 V V 3 = I 3 • R 3 V 3 = (0. 31579 A) • (20 ) V 3 = 6. 32 V

The analysis begins by using the resistance values for the individual resistors in order to determine the equivalent resistance of the circuit. Req = R 1 + R 2 + R 3 = 11 + 7 + 20 = 38 Now that the equivalent resistance is known, the current through the battery can be determined using Ohm's law equation. In using the Ohm's law equation ( V = I • R) to determine the current in the circuit, it is important to use the battery voltage for V and the equivalent resistance for R. The calculation is shown here: Itot = Vbattery / Req = (12 V) / (38 ) = 0. 31579 Amp The 1. 5 Amp value for current is the current at the battery location. For a series circuit with no branching locations, the current is everywhere the same. The current at the battery location is the same as the current at each resistor location. Subsequently, the 0. 316 Amp (rounded) is the value of I 1, I 2, and I 3. Ibattery = I 1 = I 2 = I 3 = 0. 316 Amp (rounded) There are three values left to be determined - the voltage drops across each of the individual resistors. Ohm's law is used once more to determine the voltage drops for each resistor - it is simply the product of the current at each resistor (calculated above as 0. 31579 Amp) and the resistance of each resistor (given in the problem statement). The calculations are shown below. As a check of the accuracy of the mathematics performed, it is wise to see if the calculated values satisfy the principle that the sum of the voltage drops for each individual resistor is equal to the voltage rating of the battery. In other words, is Vbattery = V 1 + V 2 + V 3 ? Is Vbattery = V 1 + V 2 + V 3 ? Is 12 V = 3. 47 V + 2. 21 V + 6. 32 V ? Is 12 V = 12 V? Yes!!

Sample problem parallel n Three resistors are connected in parallel. If placed in a circuit with a 12 -volt power supply. Determine the equivalent resistance, the total circuit current, and the voltage drop across and current in each resistor. I 1 = V 1 / R 1 I 1 = (12 V) / (11 ) I 1 = 1. 091 Amp V 2 = V 2 / R 2 I 2 = (12 V) / (7 ) I 2 = 1. 714 Amp V 3 = V 3 / R 3 I 3 = (12 V) / (20 ) I 3 = 0. 600 Amp

The analysis begins by using the resistance values for the individual resistors in order to determine the equivalent resistance of the circuit. 1 / Req = 1 / R 1 + 1 / R 2 + 1 / R 3 = (1 / 11 ) + (1 / 7 ) + (1 / 20 ) 1 / Req = 0. 283766 -1 Req = 1 / (0. 283766 -1) Req = 3. 52 (rounded from 3. 524027 ) Now that the equivalent resistance is known, the current in the battery can be determined using the Ohm's law equation. In using the Ohm's law equation ( V = I • R) to determine the current in the circuit, it is important to use the battery voltage for V and the equivalent resistance for R. The calculation is shown here: Itot = Vbattery / Req = (12 V) / (3. 524027 ) Itot = 3. 41 Amp (rounded from 3. 4051948 Amp) The 12 V battery voltage represents the gain in electric potential by a charge as it passes through the battery. The charge loses this same amount of electric potential for any given pass through the external circuit. That is, the voltage drop across each one of the three resistors is the same as the voltage gained in the battery: V battery = V 1 = V 2 = V 3 = 12 V There are three values left to be determined - the current in each of the individual resistors. Ohm's law is used once more to determine the current values for each resistor - it is simply the voltage drop across each resistor (12 Volts) divided by the resistance of each resistor (given in the problem statement). The calculations are shown below. As a check of the accuracy of the mathematics performed, it is wise to see if the calculated values satisfy the principle that the sum of the current values for each individual resistor is equal to the total current in the circuit (or in the battery). In other words, is I tot = I 1 + I 2 + I 3 ? Is Itot = I 1 + I 2 + I 3 ? Is 3. 405 Amp = 1. 091 Amp + 1. 714 Amp + 0. 600 Amp ? Is 3. 405 Amp = 3. 405 Amp? Yes!!

Parallel circuits and overloading n n n More and more appliances operated in parallel in one circuit… n Washer, dryer, fridge, etc. at same time? n Too many Christmas lights? n Blowdryer, hair straightener, hot curlers all at once? n Causes current in main branch to increase, wires can overheat Circuit breaker ‘pops’, opens a switch when specified maximum current is reached in main branch Ex: circuit breakers for 15 A, 20 A, etc.