ELECTRIC CIRCUIT ANALYSIS I Chapter 8 Methods of

ELECTRIC CIRCUIT ANALYSIS - I Chapter 8 – Methods of Analysis Lecture 9 A - Tutorial by Moeen Ghiyas 21/01/2022 1

TODAY’S LESSON CONTENTS �Branch Current Analysis �Mesh Analysis Method (General Approach) �Super Mesh Currents

Branch Current Analysis � # 16 – For the transistor configuration of Fig: a) Solve for the currents IB, IC, and IE using the fact that VBE = 0. 7 V and VCE = 8 V. b) Find the voltages VB, VC, and VE with respect to ground. c) What is the ratio of output current IC to input current IB? [Note: In transistor analysis this ratio is referred to as the dc beta of the transistor (βdc)].

Branch Current Analysis a) Solve for the currents IB, IC, and IE using the fact that VBE = 0. 7 V and VCE = 8 V. � Solution: o KVL in loop 1 o KVL in loop 2 o KCL at 1 node o Solving simultaneously

Branch Current Analysis b) Find the voltages VB, VC, and VE with respect to ground. � Solution : Using basic tools of electrical engineering. .

Branch Current Analysis c) What is the ratio of output current IC to input current IB? [Note: In transistor analysis this ratio is referred to as the dc beta of the transistor (βdc)].

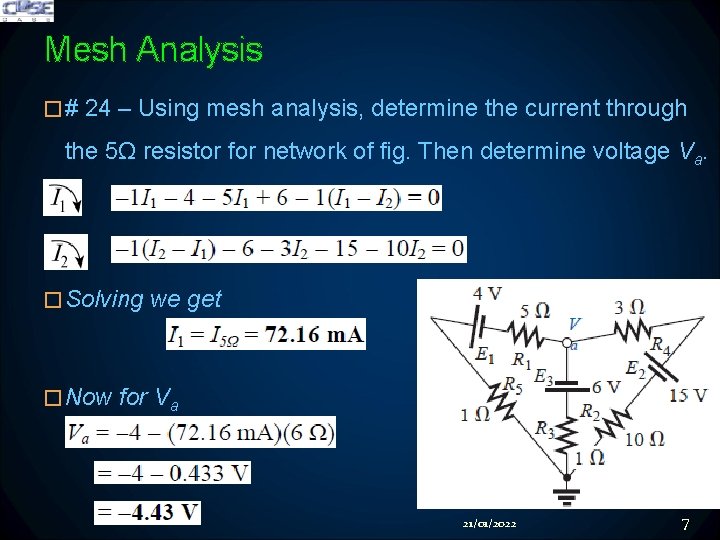
Mesh Analysis �# 24 – Using mesh analysis, determine the current through the 5Ω resistor for network of fig. Then determine voltage Va. �Solving we get �Now for Va 21/01/2022 7

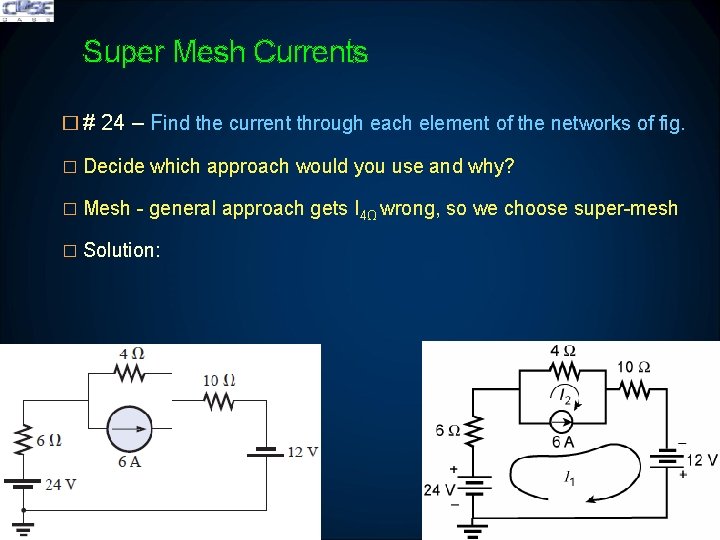
Super Mesh Currents � # 24 – Find the current through each element of the networks of fig. � Decide which approach would you use and why? � Mesh - general approach gets I 4Ω wrong, so we choose super-mesh � Solution:

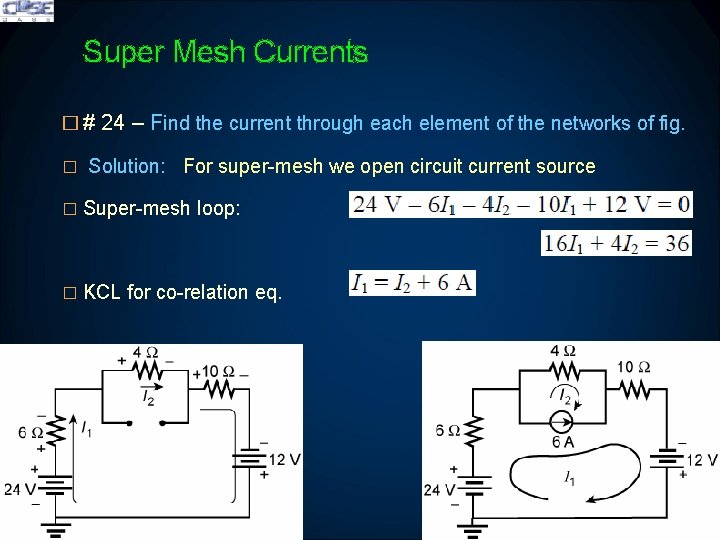
Super Mesh Currents � # 24 – Find the current through each element of the networks of fig. � Solution: For super-mesh we open circuit current source � Super-mesh loop: � KCL for co-relation eq.

Super Mesh Currents � # 24 – Find the current through each element of the networks of fig. � Simultaneous solving &

Summary / Conclusion �Determinants – (Appendix C of Book) �Mesh Analysis Method (General Approach) �Super Mesh Currents �Mesh Analysis Method (Format Approach) 21/01/2022 11

21/01/2022 12

Determinants - (2 nd Order) �Consider the following equations, where x and y are the unknown variables and a 1, a 2, b 1, b 2, c 1, and c 2 are constants: 21/01/2022 13

Determinants � Example: Solve for x and y. � Solution: � Check your answer by putting the calculated values in original equation and see if it tallies 21/01/2022 14

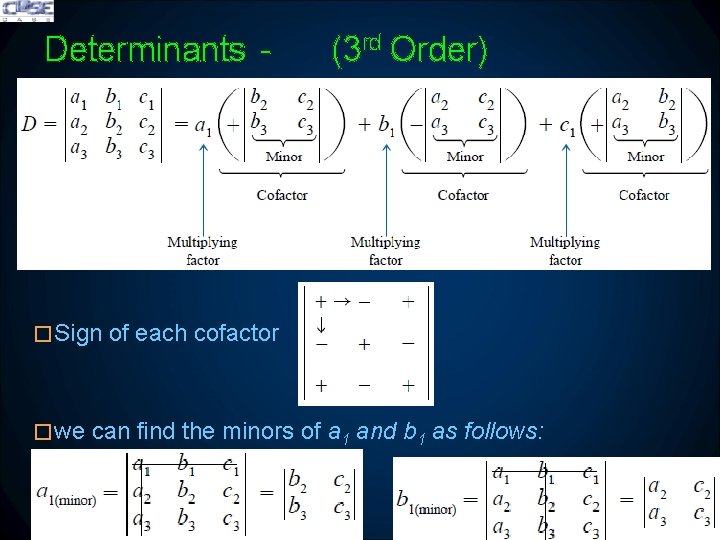
Determinants - (3 rd Order) � Consider the three following simultaneous equations in which x, y, and z are the variables, and a 1, 2, 3, b 1, 2, 3, c 1, 2, 3, and d 1, 2, 3 are constants: � where 21/01/2022 15

Determinants - (3 rd Order) �Sign of each cofactor �we can find the minors of a 1 and b 1 as follows: 21/01/2022 16