ELECTRIC CIRCUIT ANALYSIS I Chapter 15 Series Parallel

ELECTRIC CIRCUIT ANALYSIS - I Chapter 15 – Series & Parallel ac Circuits Chapter 16 – Series–Parallel ac Networks Lecture 22 by Moeen Ghiyas 30/01/2022 1

Chapter 15 – Series & Parallel ac Circuits TODAY’S lesson – Part I

Today’s Lesson Contents Chapter 15 - Series & Parallel ac Circuits � Equivalent Circuits Chapter 16 - Series-Parallel ac Networks � Reduction Methods � Ladder Networks Assignment # 4 - Submission by 10: 30 am 23 Apr 30/01/2022 3

EQUIVALENT CIRCUITS �The term equivalent refers only to the fact that for the same applied potential, the same impedance and input current will result (in the equivalent circuit). �Whether a series or parallel ac circuit, the total impedance of two or more elements in series is often equivalent to an impedance that can be achieved with fewer elements of different values �However, the equivalent elements and their values are determined by the frequency applied.

EQUIVALENT CIRCUITS � For example, for circuit of fig � The total impedance at the frequency applied is equivalent to a capacitor with a reactance of 10Ω , as shown

EQUIVALENT CIRCUITS �Always keep in mind that this equivalence is true only at the applied frequency. If the frequency changes, the reactance of each element changes, and the equivalent circuit will change — perhaps from capacitive to inductive in the above example

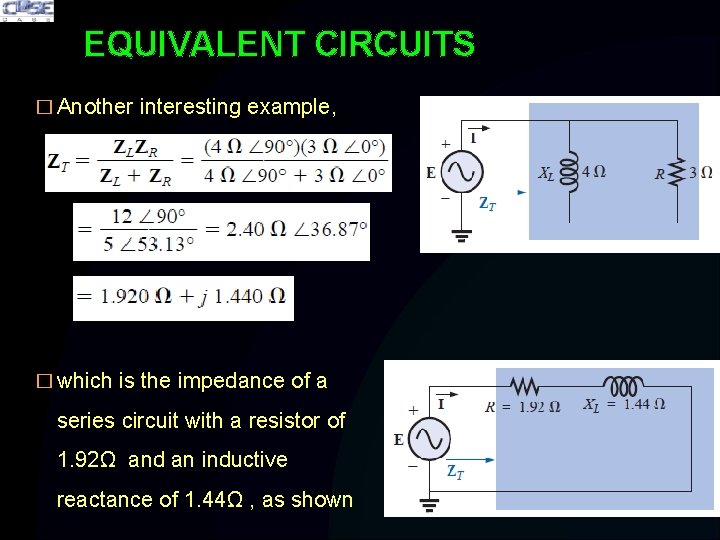
EQUIVALENT CIRCUITS � Another interesting example, � which is the impedance of a series circuit with a resistor of 1. 92Ω and an inductive reactance of 1. 44Ω , as shown

EQUIVALENT CIRCUITS � Current I will be same in equivalent circuit for same input voltage E � For a parallel circuit of one resistive element and one reactive element, the series circuit with the same input impedance will always be composed of one resistive and one reactive element. � The impedance of each element of the series circuit will be different from that of the parallel circuit, but the reactive elements will always be of the same type; i. e. , an R-L circuit and an R-C parallel circuit will have an equivalent R-L and R-C series circuit respectively � The same is true when converting from a series to a parallel circuit.

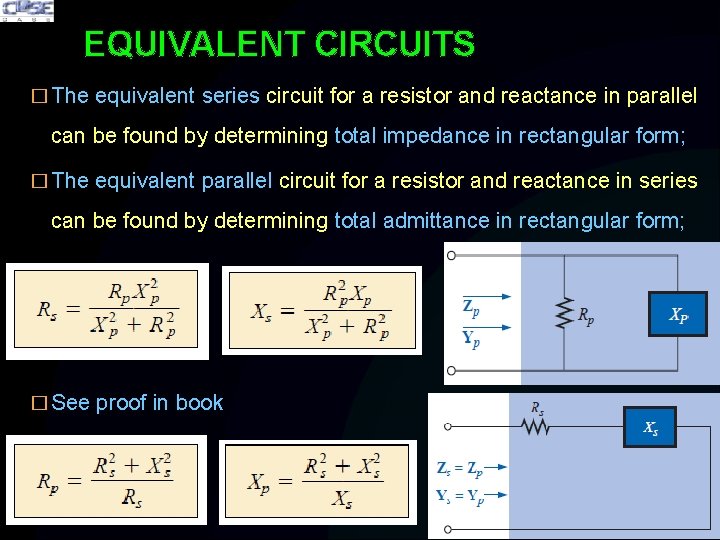
EQUIVALENT CIRCUITS � The equivalent series circuit for a resistor and reactance in parallel can be found by determining total impedance in rectangular form; � The equivalent parallel circuit for a resistor and reactance in series can be found by determining total admittance in rectangular form; � See proof in book

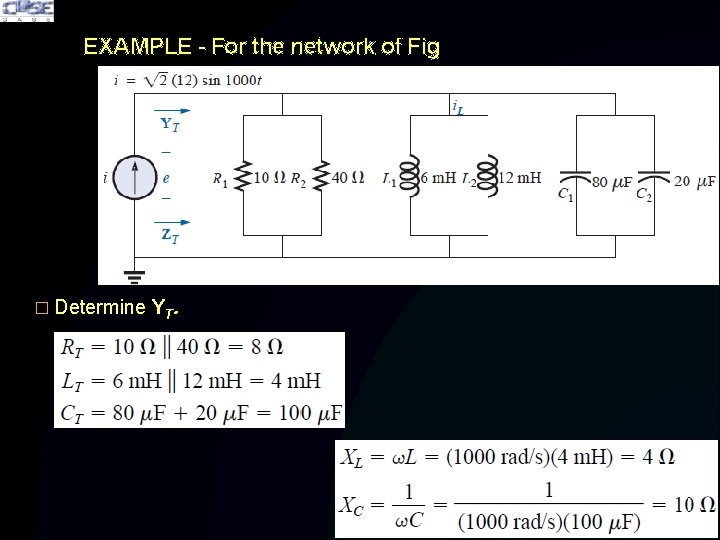
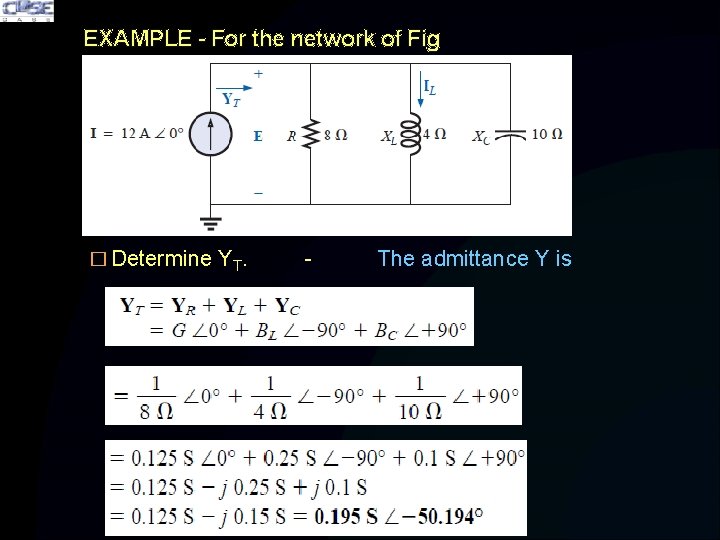
EXAMPLE - For the network of Fig � Determine YT.

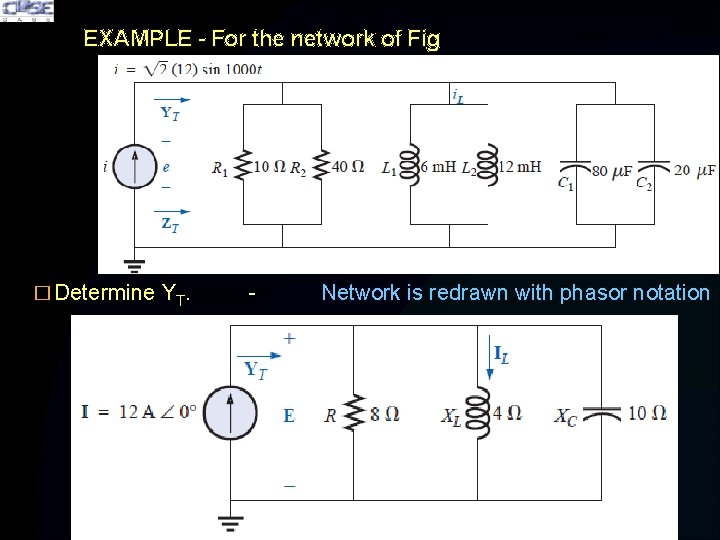
EXAMPLE - For the network of Fig � Determine YT. - Network is redrawn with phasor notation

EXAMPLE - For the network of Fig � Determine YT. - The admittance Y is

EXAMPLE - For the network of Fig � Sketch the admittance diagram.

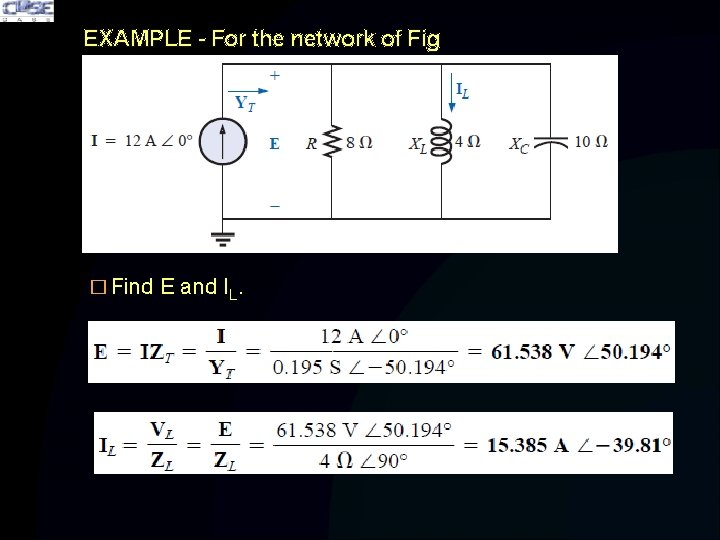
EXAMPLE - For the network of Fig � Find E and IL.

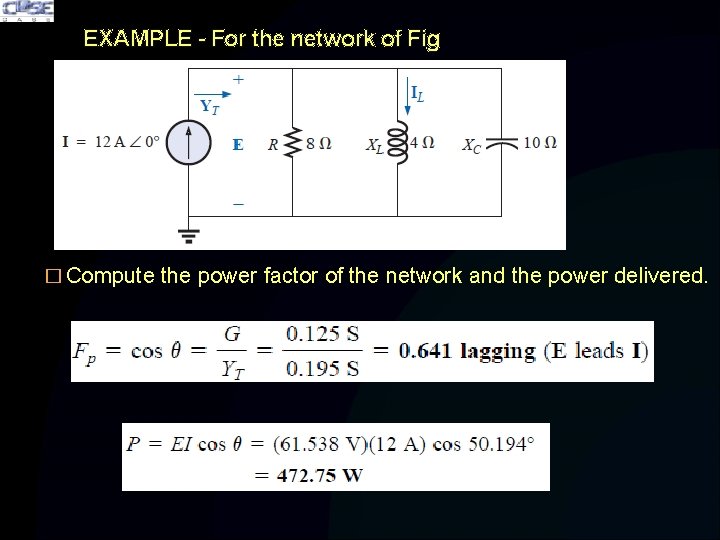
EXAMPLE - For the network of Fig � Compute the power factor of the network and the power delivered.

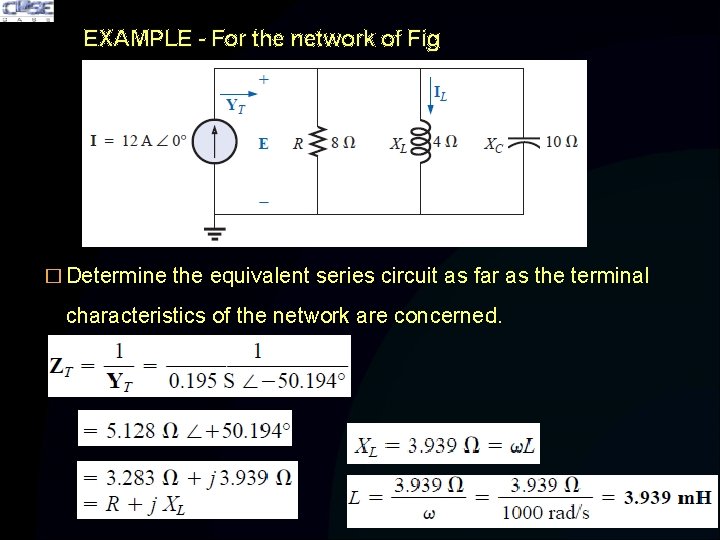
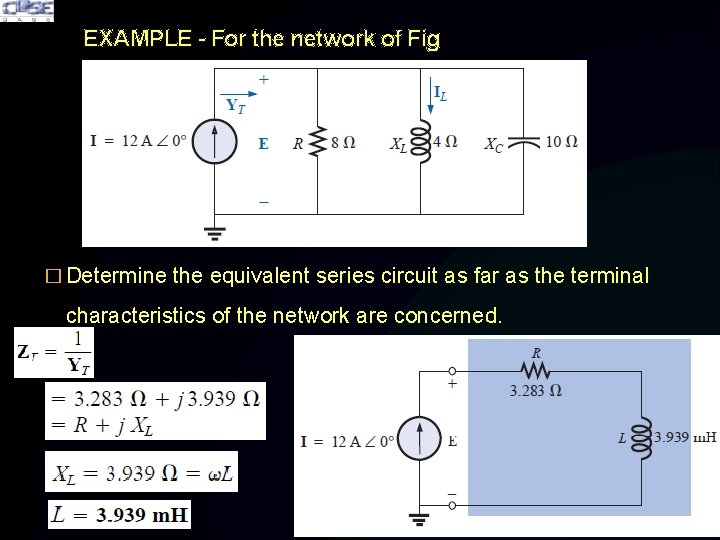
EXAMPLE - For the network of Fig � Determine the equivalent series circuit as far as the terminal characteristics of the network are concerned.

EXAMPLE - For the network of Fig � Determine the equivalent series circuit as far as the terminal characteristics of the network are concerned.

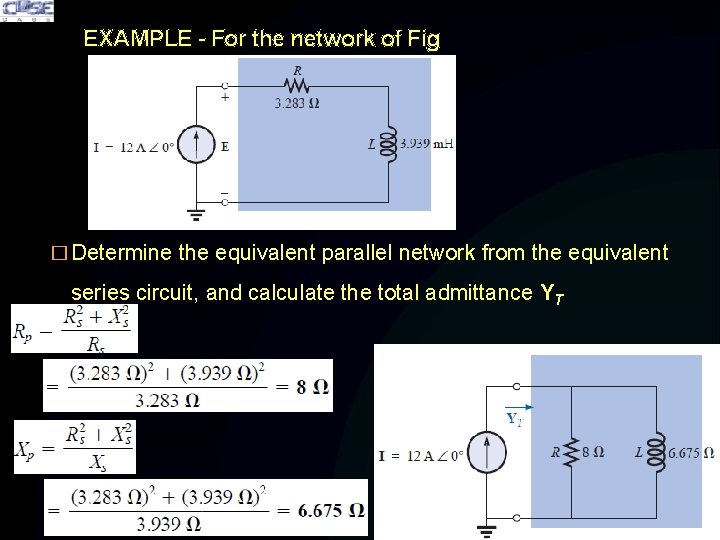
EXAMPLE - For the network of Fig � Determine the equivalent parallel network from the equivalent series circuit, and calculate the total admittance YT

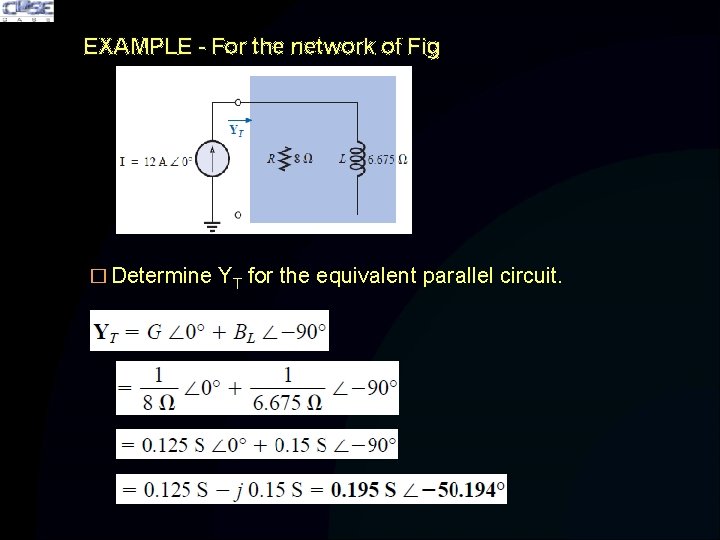
EXAMPLE - For the network of Fig � Determine YT for the equivalent parallel circuit.

Chapter 16 – Series–Parallel ac Networks TODAY’S lesson – Part II

Series-Parallel ac Networks - Approach � Reduce the network to the fundamental structure preferably towards source to determine the total impedance of the network and redraw network by combining series and parallel elements. � The source current and voltages can then be determined. � Later work back (Expand) from the source through the network to find specific quantities. � When you have arrived at a solution, check to see that it is reasonable by considering the magnitudes. If not, either solve the network using another approach, or check over your work very carefully

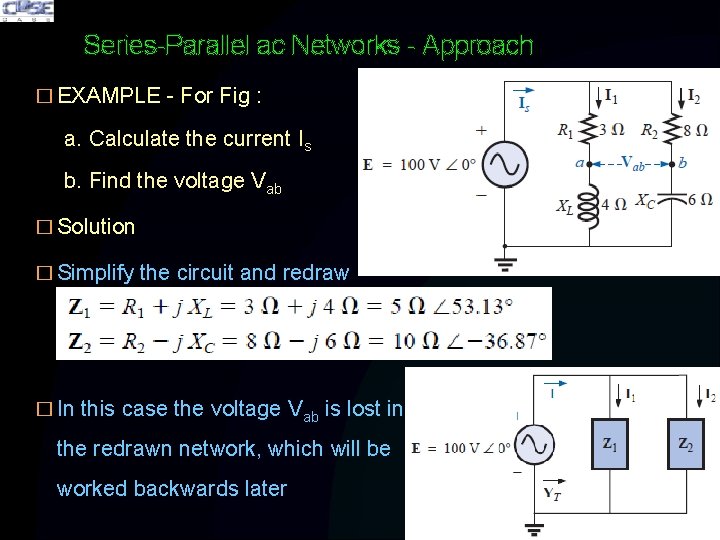
Series-Parallel ac Networks - Approach � EXAMPLE - For Fig : a. Calculate the current Is b. Find the voltage Vab � Solution � Simplify the circuit and redraw � In this case the voltage Vab is lost in the redrawn network, which will be worked backwards later

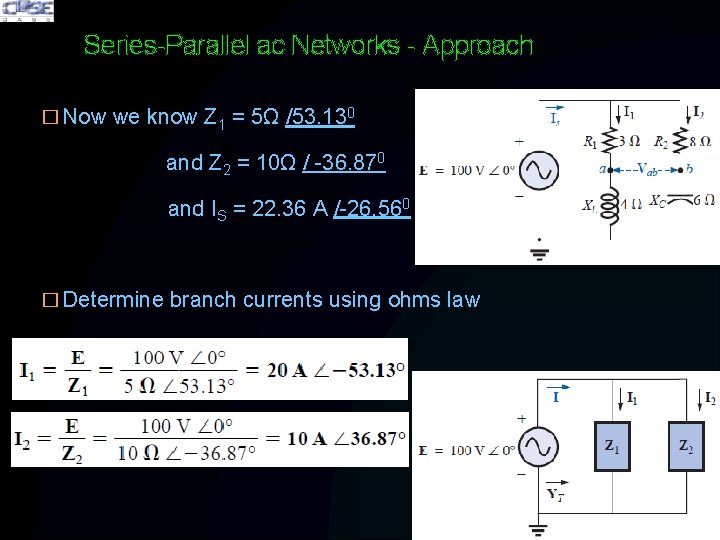
Series-Parallel ac Networks - Approach � Now we know Z 1 = 5Ω /53. 130 and Z 2 = 10Ω / -36. 870 � Determine ZT � Calculate I or IS

Series-Parallel ac Networks - Approach � Now we know Z 1 = 5Ω /53. 130 and Z 2 = 10Ω / -36. 870 and IS = 22. 36 A /-26. 560 � Determine branch currents using ohms law

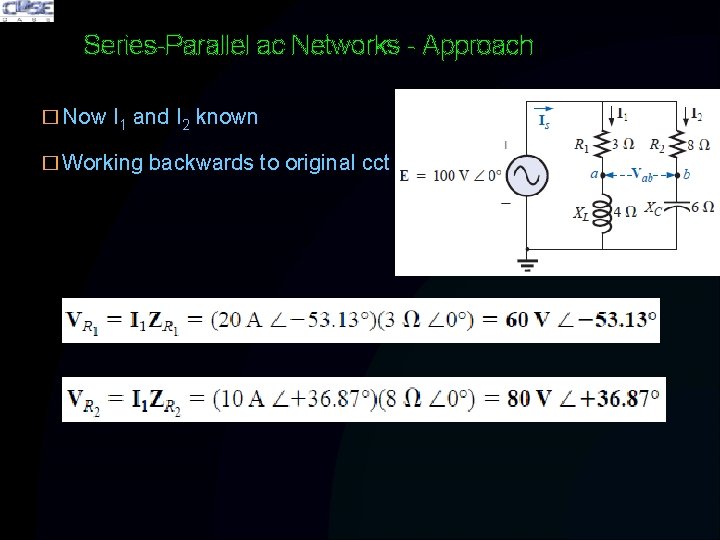
Series-Parallel ac Networks - Approach � Now I 1 and I 2 known � Working backwards to original cct

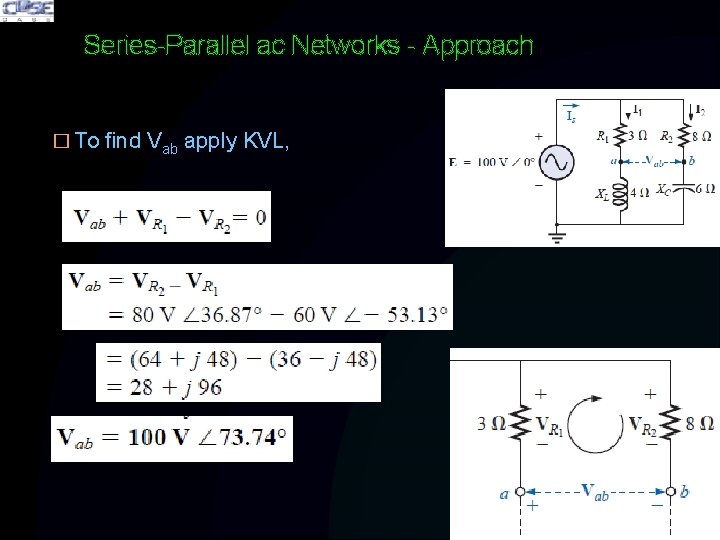
Series-Parallel ac Networks - Approach � To find Vab apply KVL,

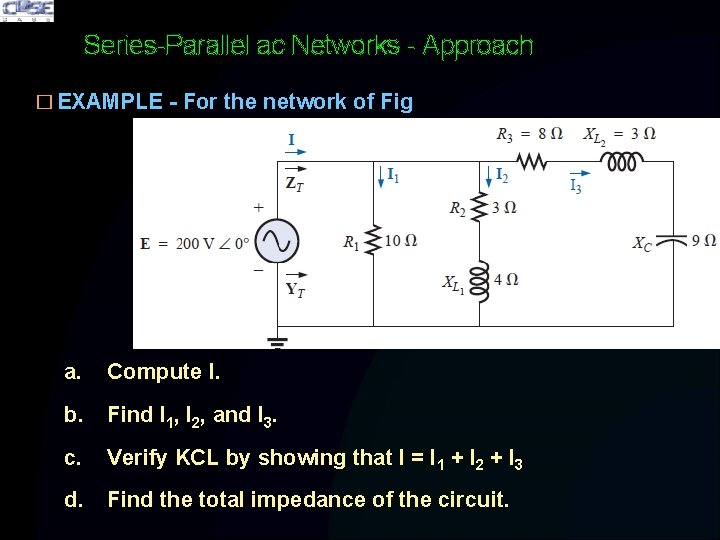
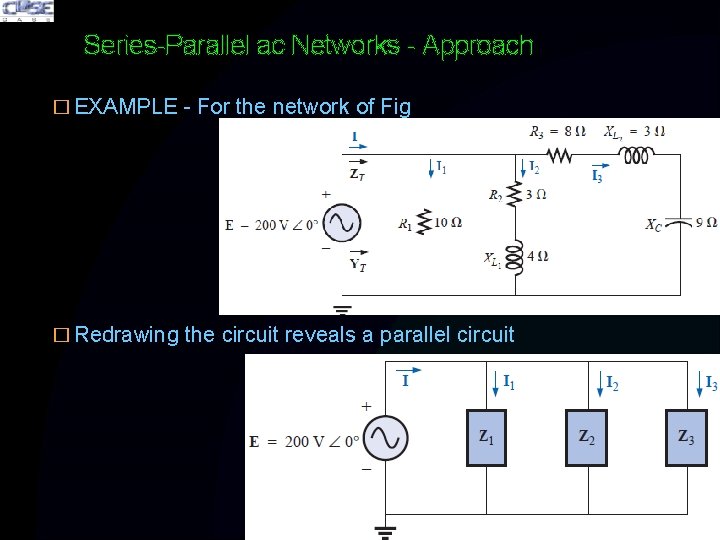
Series-Parallel ac Networks - Approach � EXAMPLE - For the network of Fig a. Compute I. b. Find I 1, I 2, and I 3. c. Verify KCL by showing that I = I 1 + I 2 + I 3 d. Find the total impedance of the circuit.

Series-Parallel ac Networks - Approach � EXAMPLE - For the network of Fig � Redrawing the circuit reveals a parallel circuit

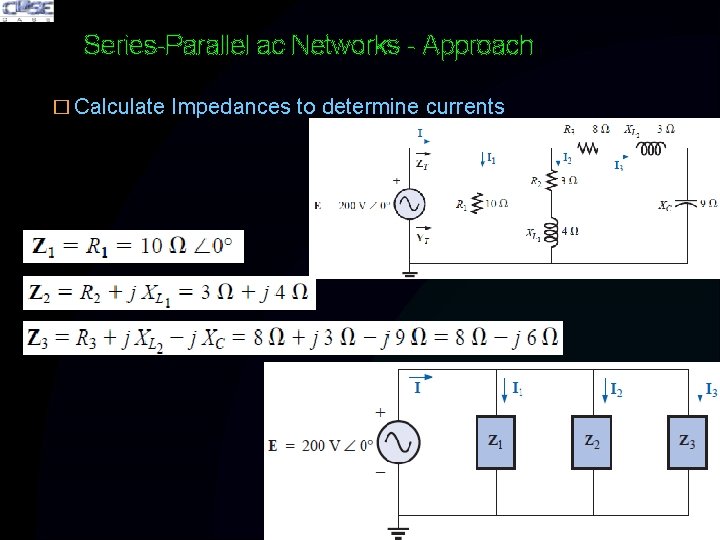
Series-Parallel ac Networks - Approach � Calculate Impedances to determine currents

Series-Parallel ac Networks - Approach � The total admittance is � The current I becomes

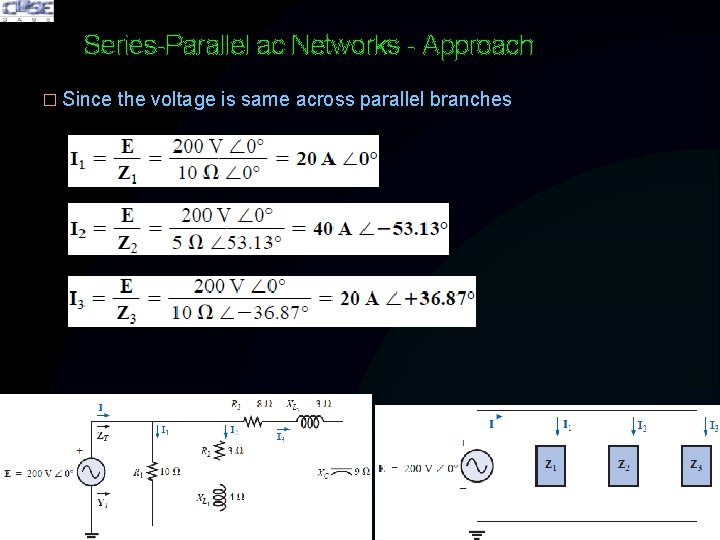
Series-Parallel ac Networks - Approach � Since the voltage is same across parallel branches

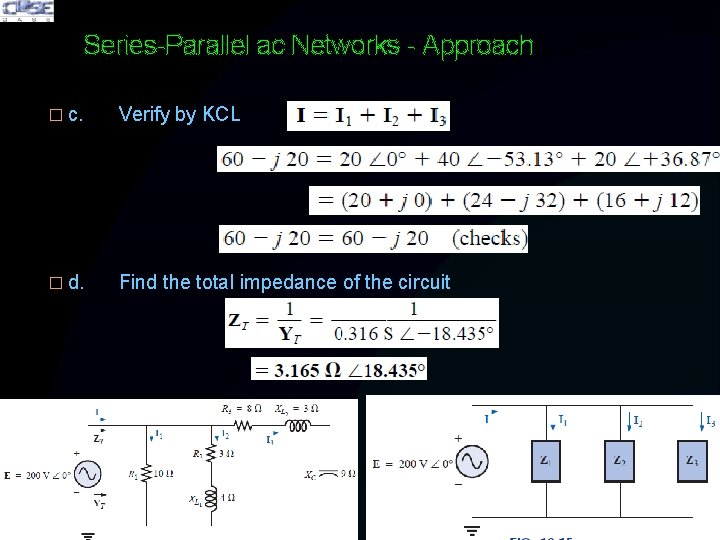
Series-Parallel ac Networks - Approach � c. Verify by KCL � d. Find the total impedance of the circuit

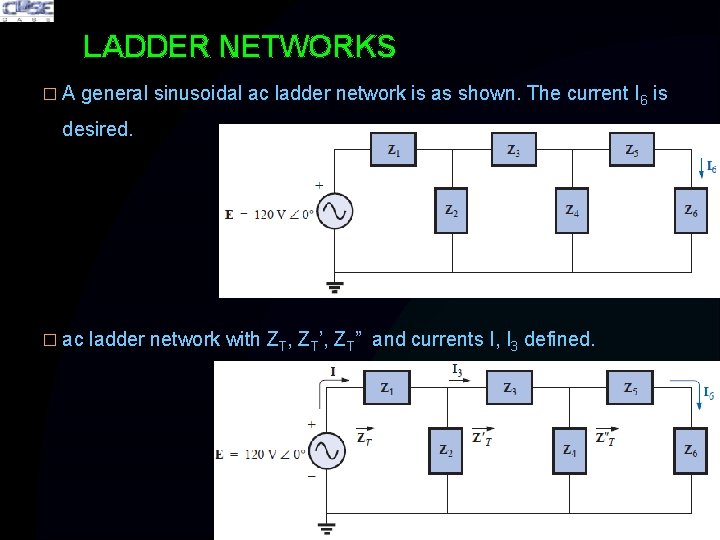
LADDER NETWORKS � A general sinusoidal ac ladder network is as shown. The current I 6 is desired. � ac ladder network with ZT, ZT’, ZT” and currents I, I 3 defined.

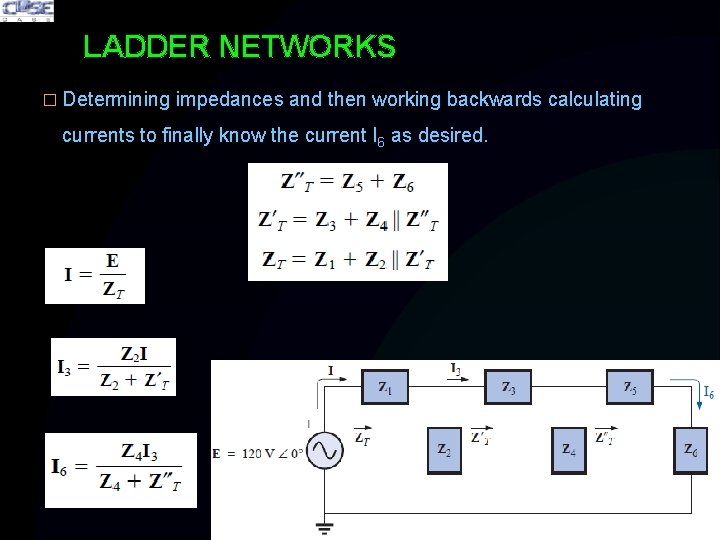
LADDER NETWORKS � Determining impedances and then working backwards calculating currents to finally know the current I 6 as desired.

Assignment # 4 � Ch 15 - Q. 17, 23, 31 � Ch 16 - Q. 11, 13 � Submission by 09: 00 am 23 Apr 2012 30/01/2022 35

Summary / Conclusion Chapter 15 - Series & Parallel ac Circuits � Equivalent Circuits Chapter 16 - Series-Parallel ac Networks � Reduction Methods � Ladder Networks Assignment # 4 - Submission by 10: 30 am 23 Apr

30/01/2022 37