ELECTRIC CIRCUIT ANALYSIS I Chapter 13 Sinusoidal Alternating

ELECTRIC CIRCUIT ANALYSIS - I Chapter 13 – Sinusoidal Alternating Waveforms Lecture 12 by Moeen Ghiyas 17/12/2021 1

CHAPTER 13 – Sinusoidal Alternating Waveforms TODAY’S lesson

TODAY’S LESSON CONTENTS �Introduction – Sinusoidal Alternating Waveforms �Definitions �Defined Polarities & Direction �The Sine Wave

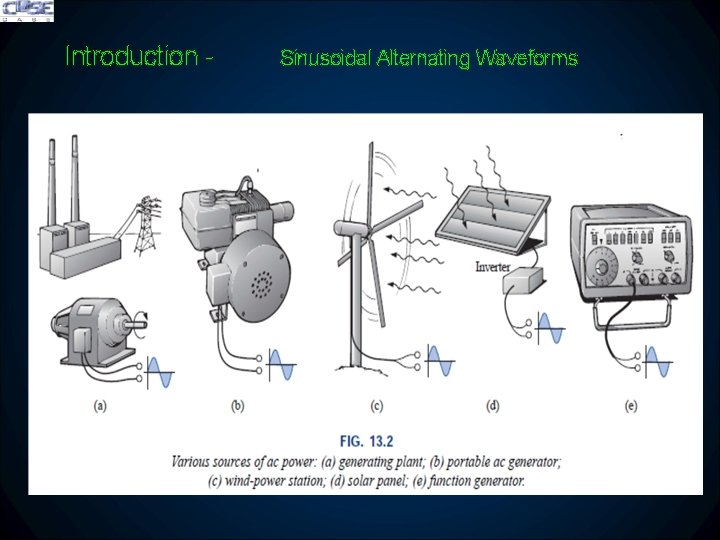
Introduction - Sinusoidal Alternating Waveforms � AC networks are those in which the magnitude of the source is the time-varying voltage or current � Letters ac are an abbreviation for alternating current � The term alternating indicates only that the waveform alternates between two prescribed levels in a set time sequence � The pattern of particular interest is the sinusoidal ac waveform for voltage

Introduction - Sinusoidal Alternating Waveforms

Definitions � Referance the diagram, the vertical scaling is in volts or amperes and the horizontal scaling is always in units of time � Waveform: The path traced by a quantity, such as the voltage � Instantaneous value: The magnitude of a waveform at any instant of time; denoted by lowercase letters (e 1, e 2) � Peak amplitude: The maximum value of a waveform as measured from its average, or mean, value, denoted by uppercase letters (such as Em for sources Vm for the voltage drop across a load)

Definitions � Peak value: The maximum instantaneous value of a function as measured from the zero-volt level. For the waveform of Fig shown, the peak amplitude and peak value are the same, since the average value of the function is zero volts. � Peak-to-peak value: Denoted by Ep-p or Vp-p, the full voltage between positive and negative peaks of the waveform � Periodic waveform: A waveform that continually repeats itself after the same time interval. � Period (T ): The time interval between successive repetitions

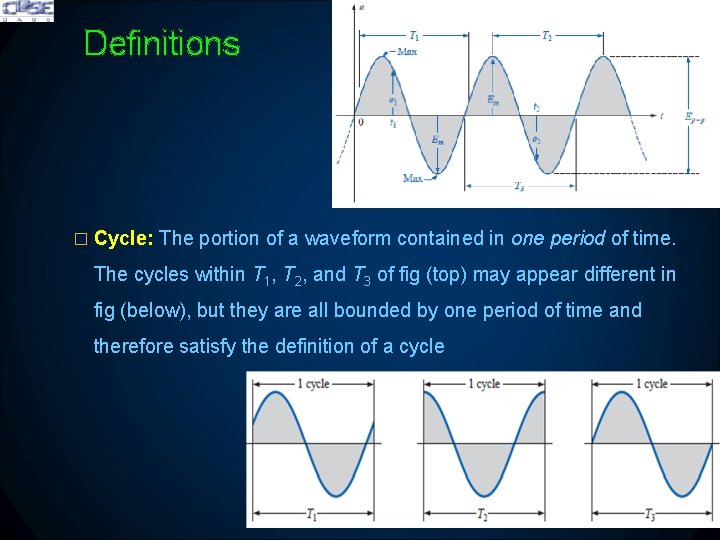
Definitions � Cycle: The portion of a waveform contained in one period of time. The cycles within T 1, T 2, and T 3 of fig (top) may appear different in fig (below), but they are all bounded by one period of time and therefore satisfy the definition of a cycle

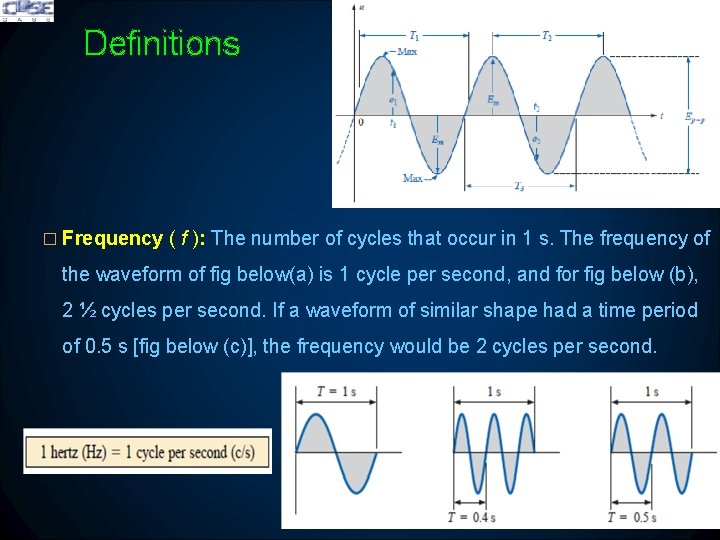
Definitions � Frequency ( f ): The number of cycles that occur in 1 s. The frequency of the waveform of fig below(a) is 1 cycle per second, and for fig below (b), 2 ½ cycles per second. If a waveform of similar shape had a time period of 0. 5 s [fig below (c)], the frequency would be 2 cycles per second.

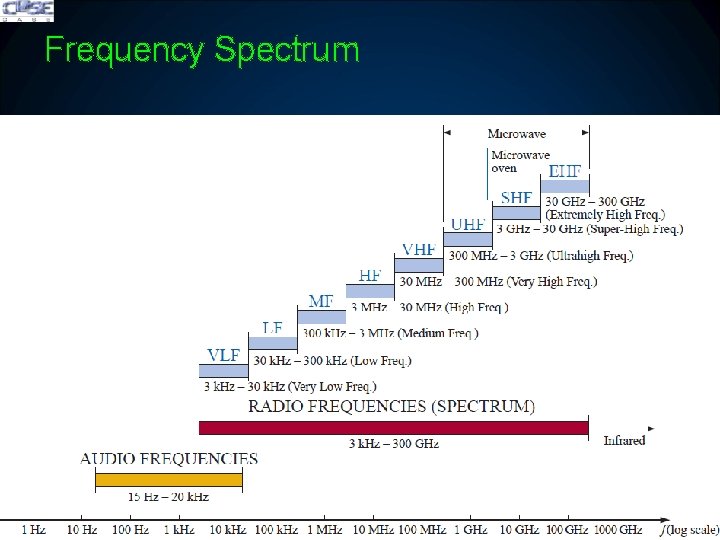
Frequency Spectrum 17/12/2021 10

Frequency Spectrum 17/12/2021 11

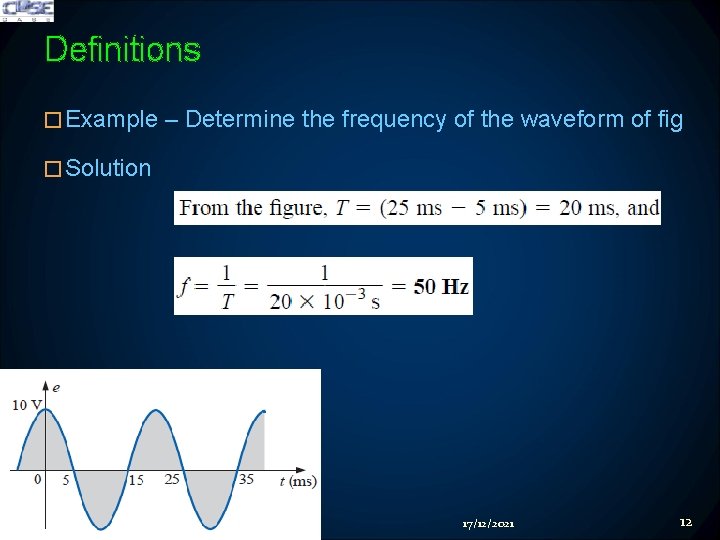
Definitions �Example – Determine the frequency of the waveform of fig �Solution 17/12/2021 12

Defined Polarities & Direction � The polarity and current direction will be for an instant of time � A lowercase letter is employed for each to indicate that the quantity is time dependent

The Sine Wave � Why use sinusoidal waveform in ac and why not square or triangular? � Ans. The sinusoidal waveform is the only alternating waveform whose shape is unaffected by the response characteristics of resistor R, inductor L, and capacitor C elements.

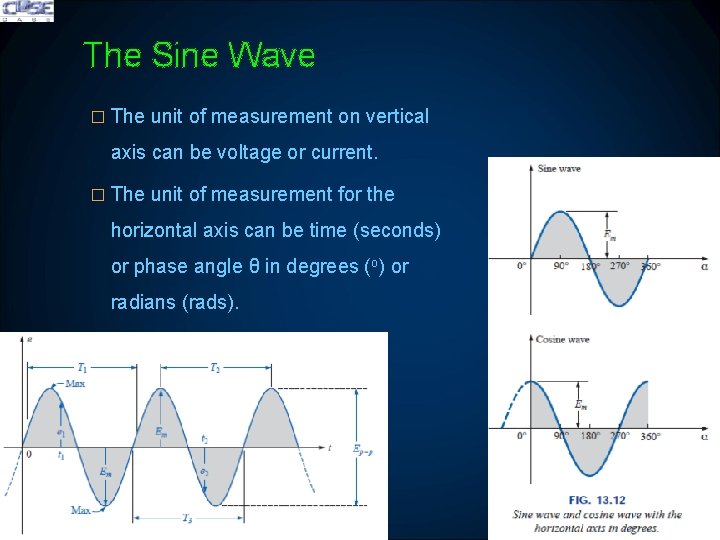
The Sine Wave � The unit of measurement on vertical axis can be voltage or current. � The unit of measurement for the horizontal axis can be time (seconds) or phase angle θ in degrees (o) or radians (rads).

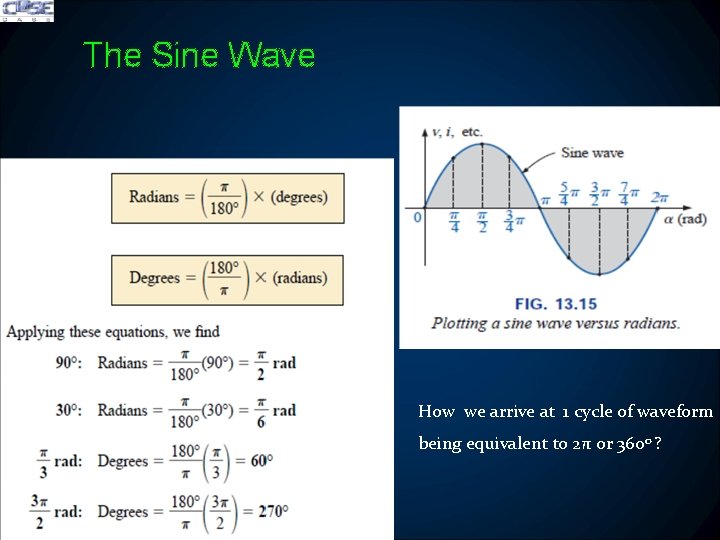
The Sine Wave How we arrive at 1 cycle of waveform being equivalent to 2π or 3600 ?

The Sine Wave � We define radian as shown in diagram � We know that circumference of the circle is C = 2 π r � Thus the quantity π is the ratio of the circumference of a circle to its diameter i. e, π = C / 2 r or π=C/d

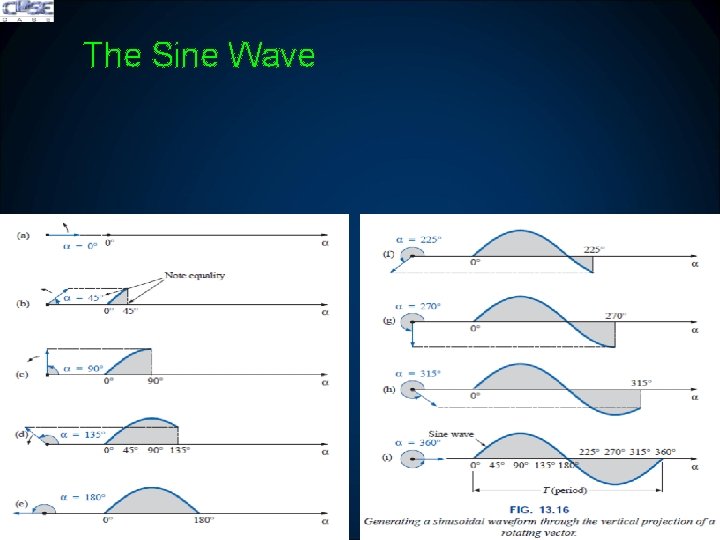
The Sine Wave � A sinusoidal waveform can be derived from the length of the vertical projection of a radius vector rotating in a uniform circular motion about a fixed point � The velocity with which the radius vector rotates about the centre, called the angular velocity, can be determined from the following equation (S = vt):

The Sine Wave

The Sine Wave � The velocity with which the radius vector rotates about the centre, called the angular velocity, can be determined from the following equation (S = vt): � Substituting into equation (above) and assigning the Greek letter omega (ω) to the angular velocity, we have

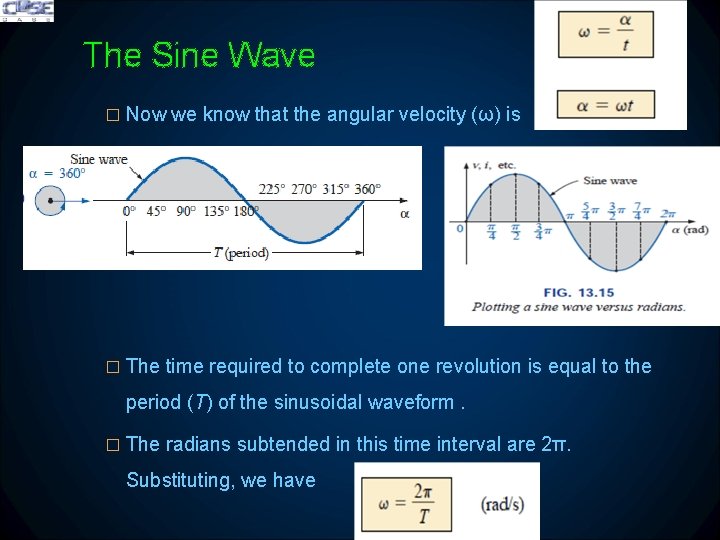
The Sine Wave � Now we know that the angular velocity (ω) is � The time required to complete one revolution is equal to the period (T) of the sinusoidal waveform. � The radians subtended in this time interval are 2π. Substituting, we have

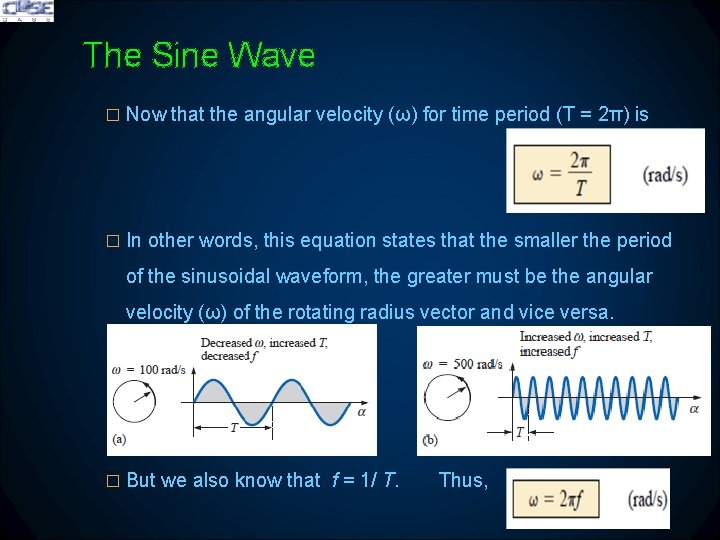
The Sine Wave � Now that the angular velocity (ω) for time period (T = 2π) is � In other words, this equation states that the smaller the period of the sinusoidal waveform, the greater must be the angular velocity (ω) of the rotating radius vector and vice versa. � But we also know that f = 1/ T. Thus,

The Sine Wave - Class Test � EXAMPLE - Determine the angular velocity of a sine wave having a frequency of 60 Hz. � EXAMPLE - Given ω = 200 rad/s, determine how long it will take the sinusoidal waveform to pass through an angle of 90°. � EXAMPLE - Find the angle through which a sinusoidal waveform of 60 Hz will pass in a period of 5 ms.

The Sine Wave - Class Test Solution � EXAMPLE - Determine the angular velocity of a sine wave having a frequency of 60 Hz. � Solution � EXAMPLE - Given ω = 200 rad/s, determine how long it will take the sinusoidal waveform to pass through an angle of 90°. � Solution

The Sine Wave - Class Test Solution � EXAMPLE - Find the angle through which a sinusoidal waveform of 60 Hz will pass in a period of 5 ms. � Solution � Note: Whenever, the relationship involving ω is to be used α will be used or interpreted in radians, because of π factor in ω = 2πf.

Summary / Conclusion � Introduction – Sinusoidal Alternating Waveforms � Definitions � Defined Polarities & Direction � The Sine Wave

17/12/2021 27