ELECTRIC CIRCUIT 2 EET 141 Chapter 1 INDUCTANCE




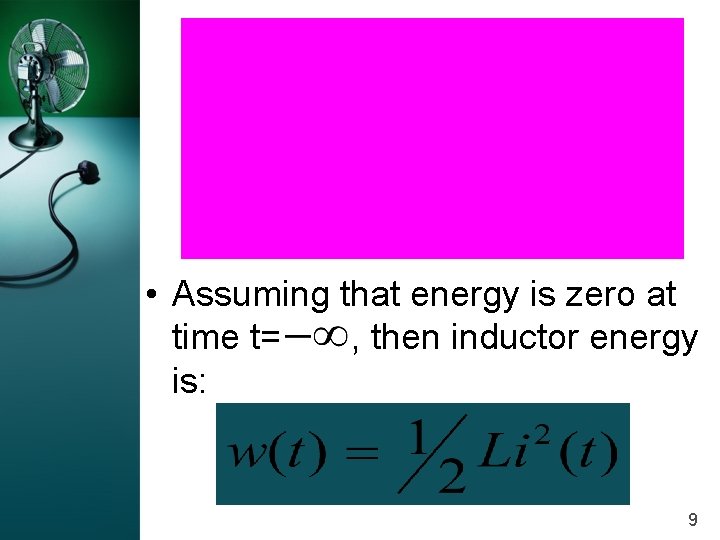


















- Slides: 47

ELECTRIC CIRCUIT 2 EET 141 (Chapter 1) INDUCTANCE & CAPACITANCE

INDUCTANCE • Characteristic of inductor • Relationship between voltage, current, power, and energy for inductance • Series parallel combinations for inductance

Inductors • An inductor is a passive two terminal electrical component designed to store energy in its magnetic field. • A practical inductor is usually formed into a cylindrical coil with many turns of conducting wire. 3

Inductors • Inductance, L is the property whereby an inductor exhibits opposition to the change of current flowing through it, measured in henrys (H). • The unit of inductors is Henry (H), m. H (10– 3) and H (10– 6). • Inductance of an inductor depends on its physical dimension and construction. 4

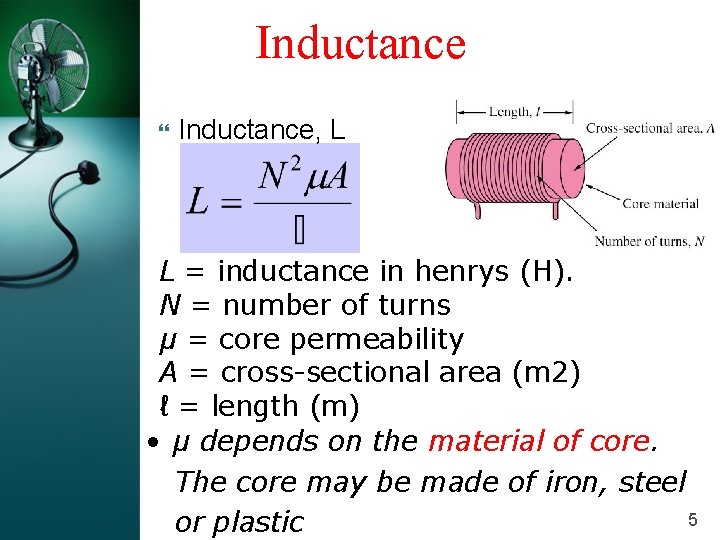
Inductance Inductance, L L = inductance in henrys (H). N = number of turns µ = core permeability A = cross-sectional area (m 2) ℓ = length (m) • µ depends on the material of core. The core may be made of iron, steel 5 or plastic

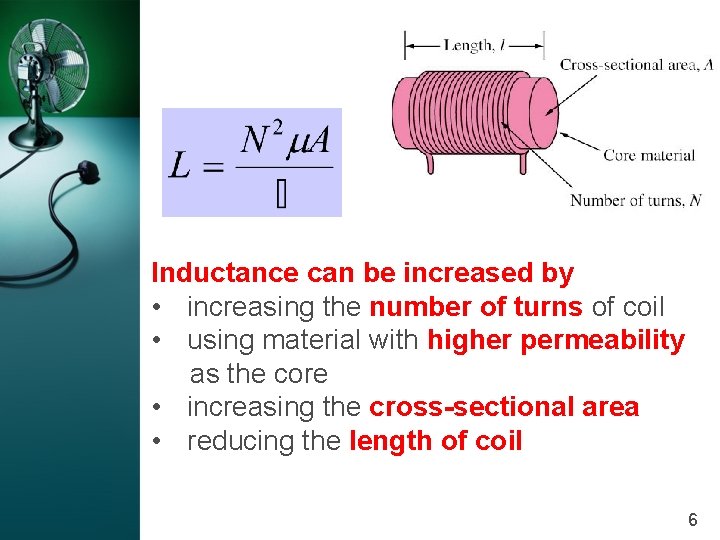
Inductance can be increased by • increasing the number of turns of coil • using material with higher permeability as the core • increasing the cross-sectional area • reducing the length of coil 6

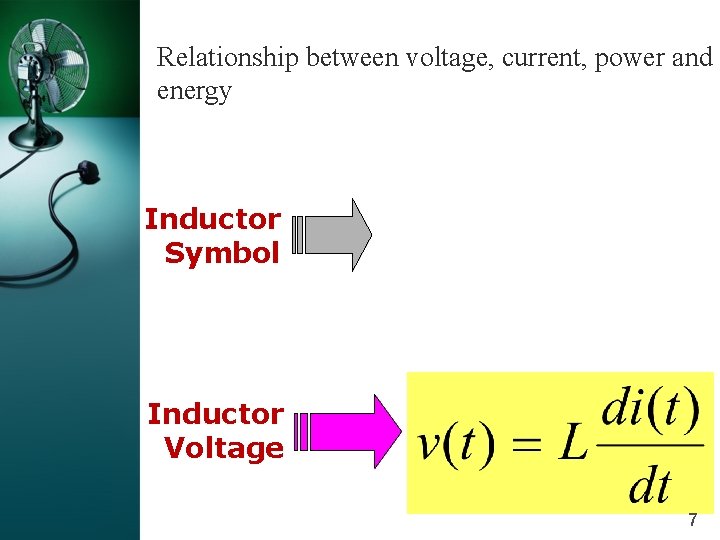
Relationship between voltage, current, power and energy Inductor Symbol Inductor Voltage 7

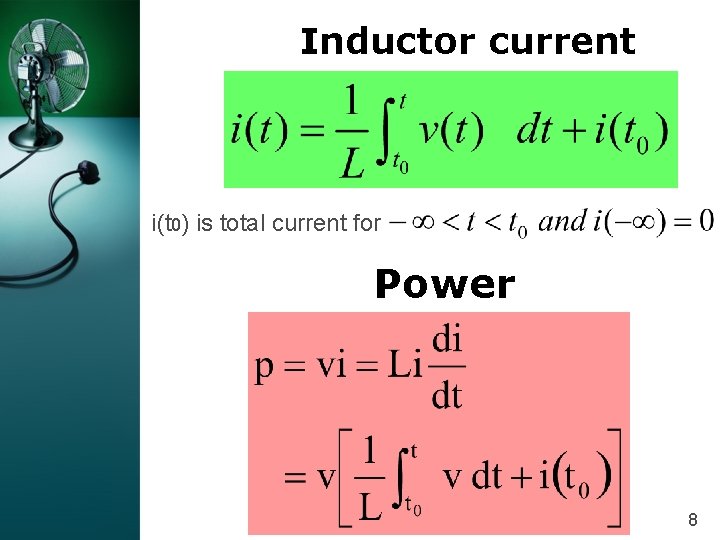
Inductor current i(t 0) is total current for Power 8
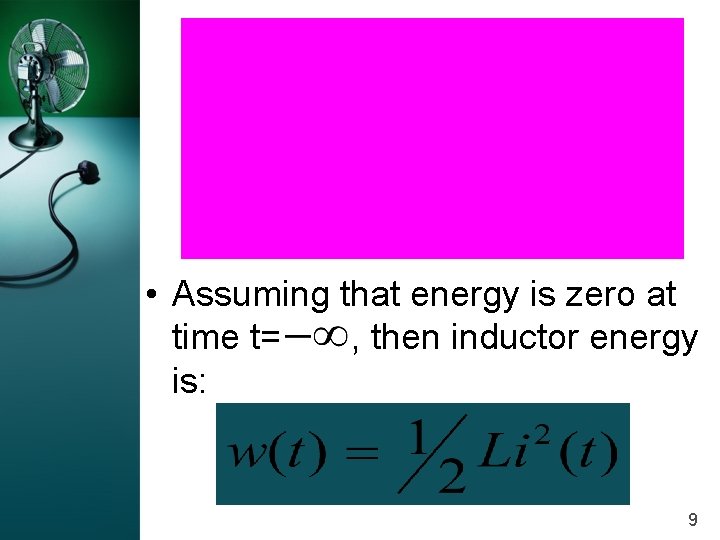
• Assuming that energy is zero at time t= , then inductor energy is: 9

An inductor: ØActs like a short circuit to dc ØThe current through an inductor cannot change instantaneously Ø Voltage across an inductor can change abruptly ØAn ideal inductor does not dissipate energy Ø Practically, non-ideal inductor has significant resistive components so it will dissipate energy 10

Example 1 The terminal voltage of a 2 -H inductor is v = 10(1 -t) V. Find the current flowing through it at t = 4 s and the energy stored in it within 0 < t < 4 s. Assume i(0) = 2 A. Answer: i(4 s) = -18 A w(4 s) = 320 J 11

v = 10(1 -t) V, L=2 H 0 < t < 4 s. Assume i(0) = 2 A 12

v = 10(1 -t) V, L=2 H 0 < t < 4 s. Assume i(0) = 2 A 13

Exercise 1 Determine the current through a 10 H inductor if the voltage across it is. Also find the energy stored at t=3 s. Assume i(0)=0. Ans: i(t) = 0. 3 t 3+2 t A W = 994. 05 J

Example 2 If the current through a 1 m. H inductor is i(t)=20 cos (100 t) m. A, find the terminal voltage and energy stored. 15

To find terminal voltage 16

To find energy stored 17

Exercise 2 Determine the current through 3 m. H inductor if the voltage is Then find the energy stored. Assume i(0)=0. Ans: i(t) = 75 sin 200 t A W = 8. 4375 sin 2 200 t J

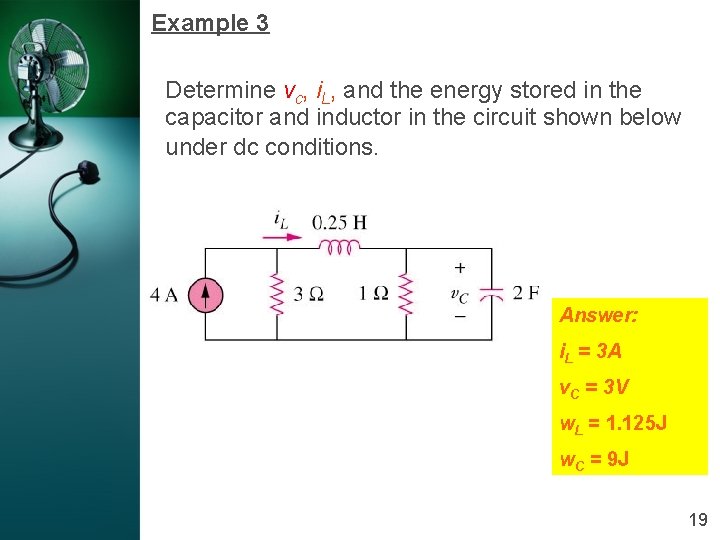
Example 3 Determine vc, i. L, and the energy stored in the capacitor and inductor in the circuit shown below under dc conditions. Answer: i. L = 3 A v. C = 3 V w. L = 1. 125 J w. C = 9 J 19

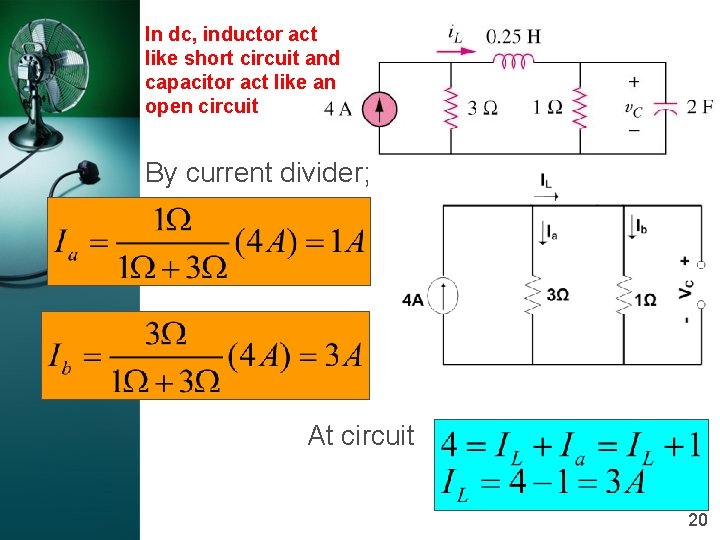
In dc, inductor act like short circuit and capacitor act like an open circuit By current divider; At circuit 20

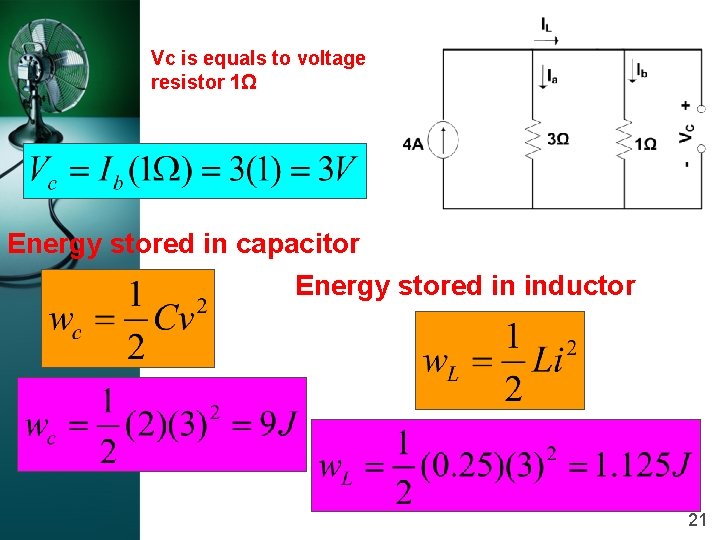
Vc is equals to voltage at resistor 1Ω Energy stored in capacitor Energy stored in inductor 21

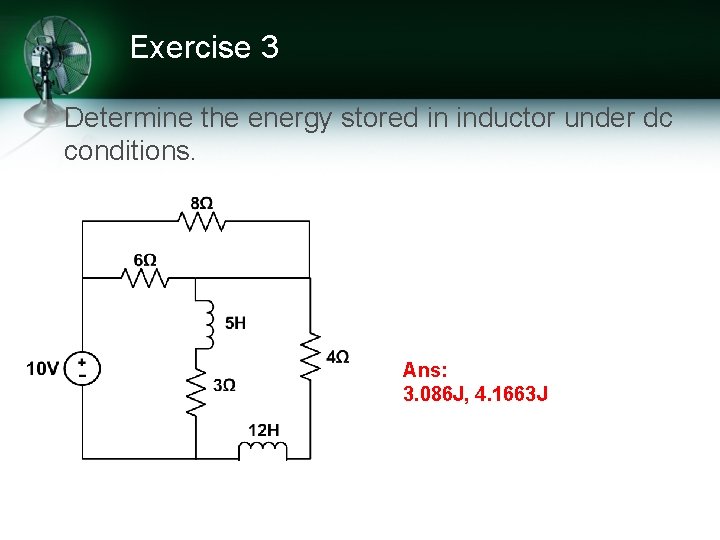
Exercise 3 Determine the energy stored in inductor under dc conditions. Ans: 3. 086 J, 4. 1663 J

Exercise 4 Determine the energy stored in the capacitor and inductor in the circuit shown below under dc conditions. Ans: WC 1 = 4. 564 J WC 2 = 24. 792 J WL = 23. 867 J

Series and Parallel Inductors • The equivalent inductance of series-connected inductors is the sum of the individual inductances. 24

Series and Parallel Inductors • The equivalent capacitance of parallel inductors is the reciprocal of the sum of the reciprocals of the Individual inductances. 25

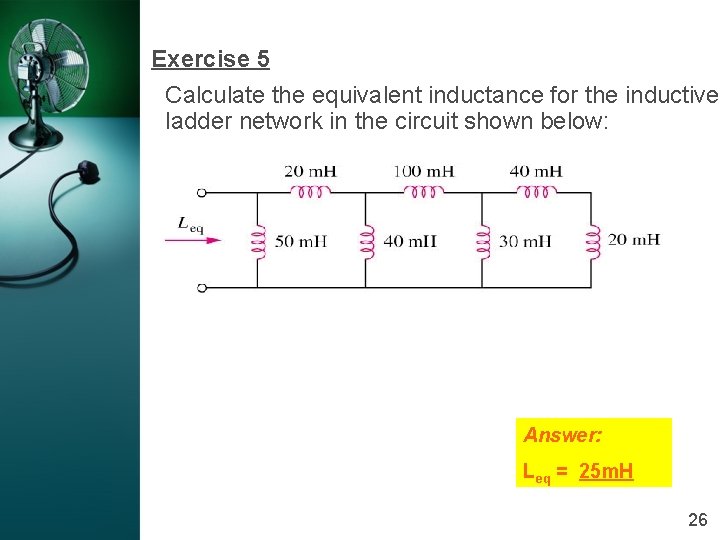
Exercise 5 Calculate the equivalent inductance for the inductive ladder network in the circuit shown below: Answer: Leq = 25 m. H 26

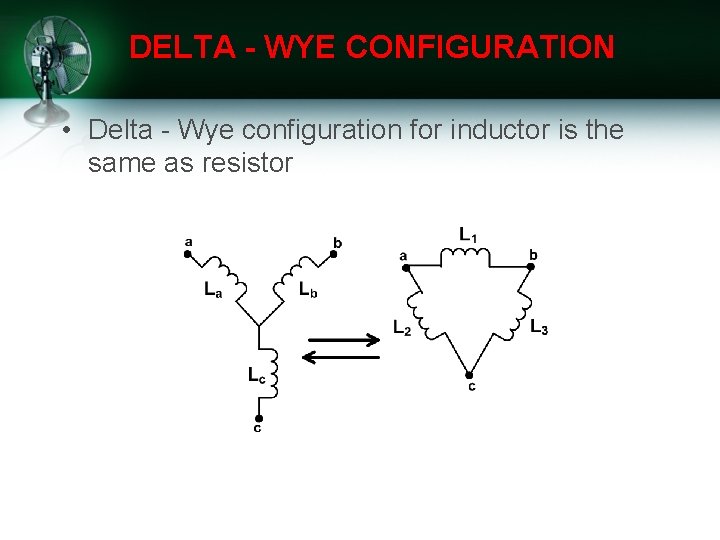
DELTA - WYE CONFIGURATION • Delta - Wye configuration for inductor is the same as resistor

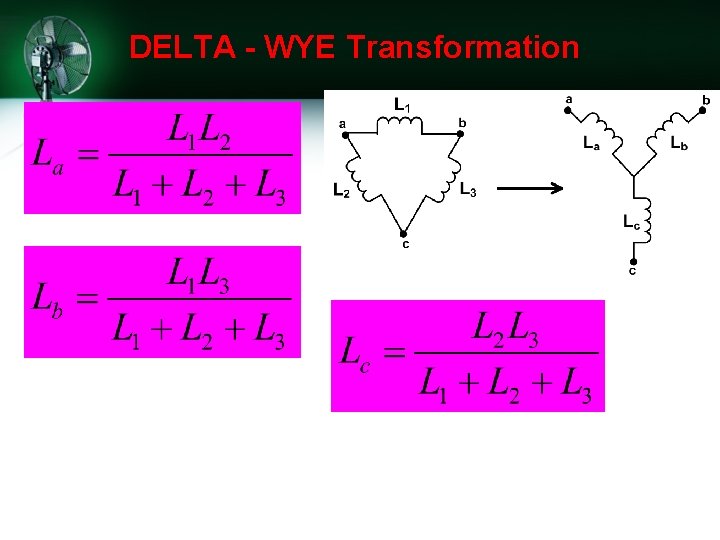
DELTA - WYE Transformation

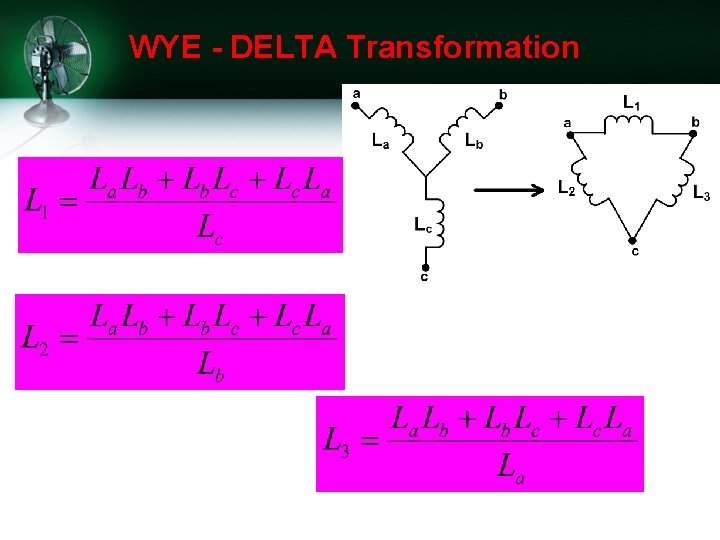
WYE - DELTA Transformation

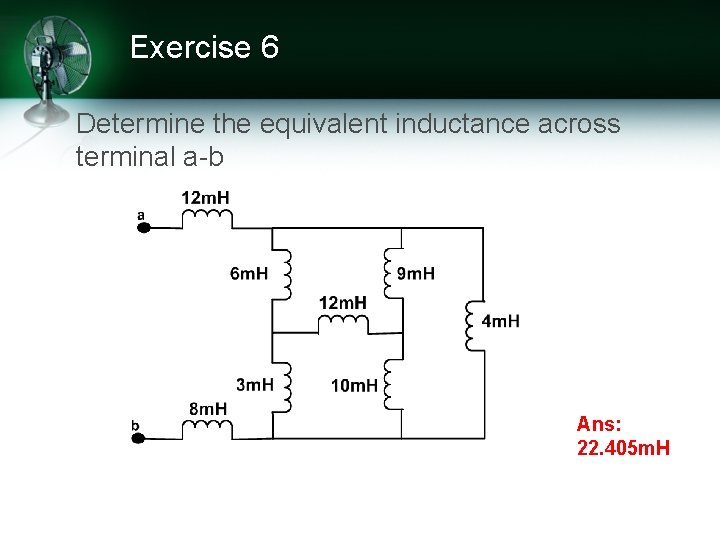
Exercise 6 Determine the equivalent inductance across terminal a-b Ans: 22. 405 m. H

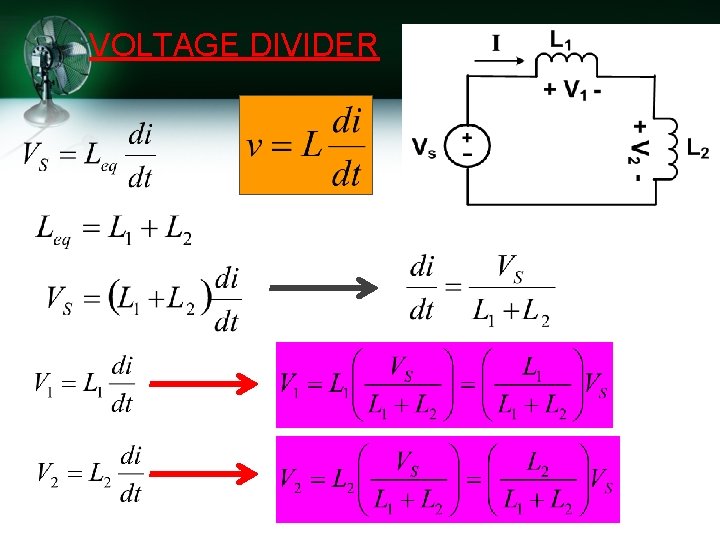
VOLTAGE DIVIDER

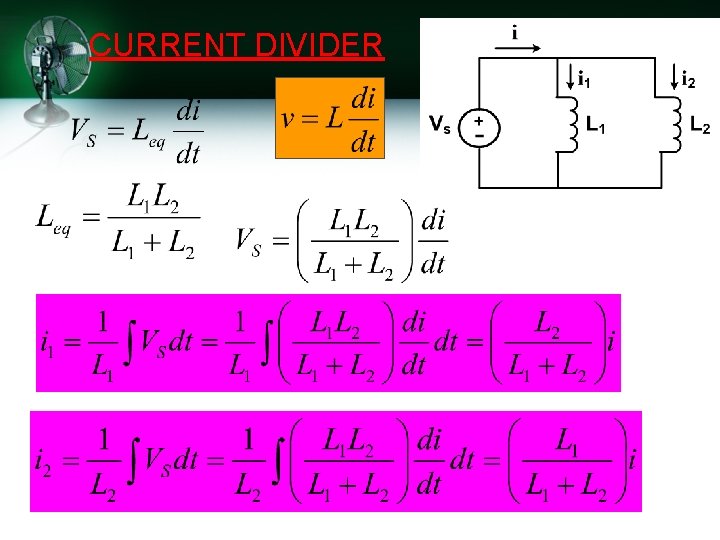
CURRENT DIVIDER

SUMMARY • Current and voltage relationship for R, L, C + + + 33

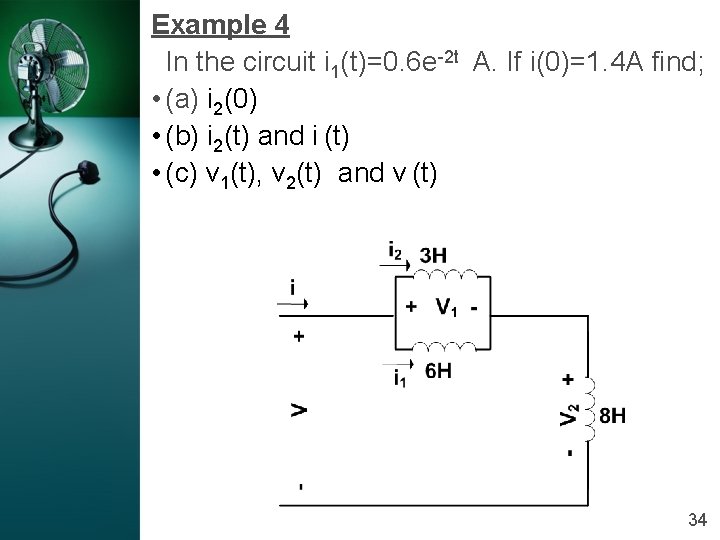
Example 4 In the circuit i 1(t)=0. 6 e-2 t A. If i(0)=1. 4 A find; • (a) i 2(0) • (b) i 2(t) and i (t) • (c) v 1(t), v 2(t) and v (t) 34

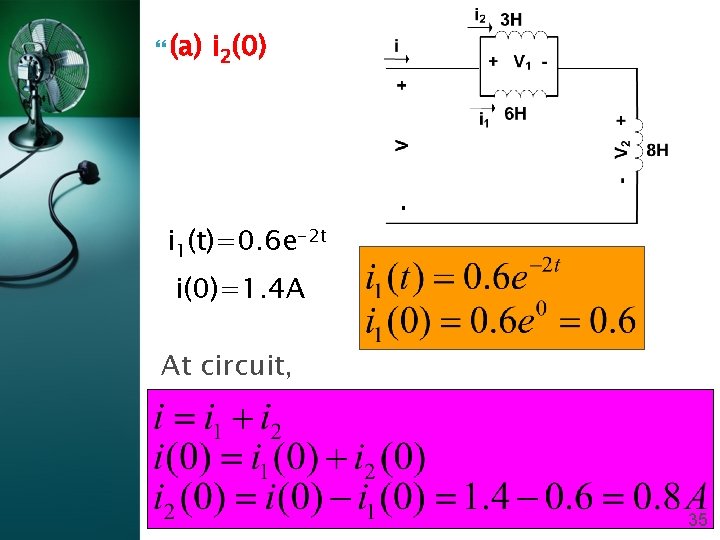
(a) i 2(0) i 1(t)=0. 6 e-2 t i(0)=1. 4 A At circuit, 35

(b) i 2(t) and i (t) i 1(t)=0. 6 e-2 t 36

37

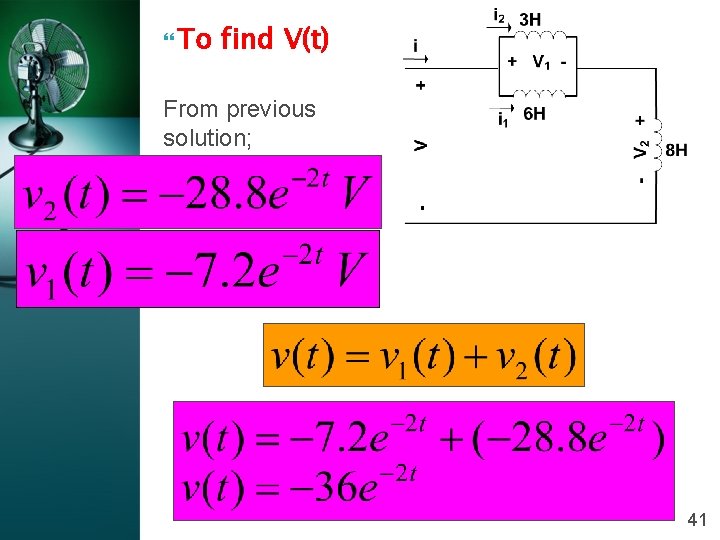
To find i (t) i 1(t)=0. 6 e-2 t From previous solution; 38

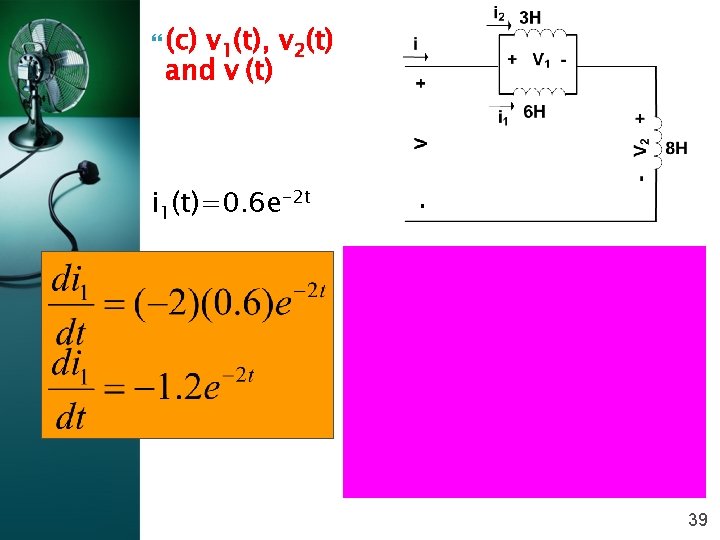
(c) v 1(t), v 2(t) and v (t) i 1(t)=0. 6 e-2 t 39

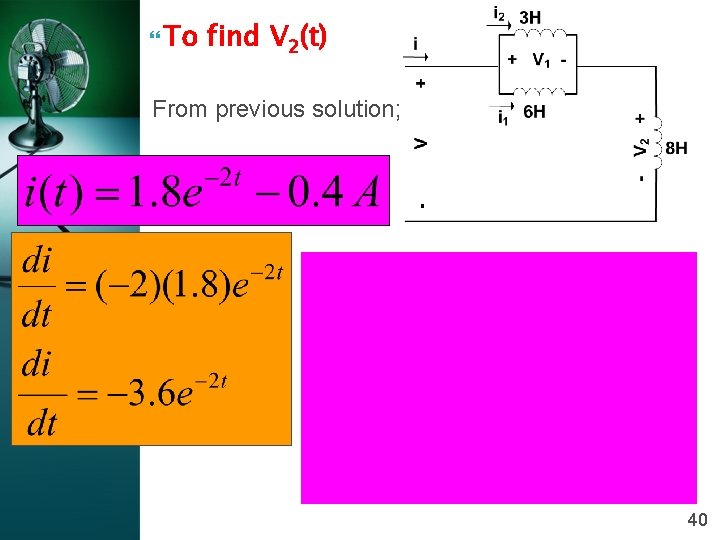
To find V 2(t) From previous solution; 40

To find V(t) From previous solution; 41

IMPORTANT NOTES! • From v =L di/dt, if current is constant, v = 0. Therefore inductor acts like a short cct to dc • Inductor opposes the change of current flowing through it. Therefore the current through inductor cannot change abruptly • Ideal inductors are assume to have zero internal resistance but non ideal (practical) inductors always have internal resistance r. L 42

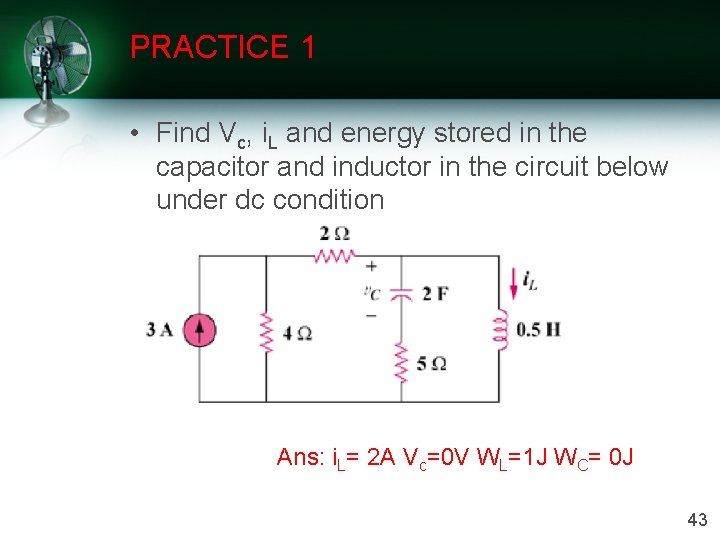
PRACTICE 1 • Find Vc, i. L and energy stored in the capacitor and inductor in the circuit below under dc condition Ans: i. L= 2 A Vc=0 V WL=1 J WC= 0 J 43

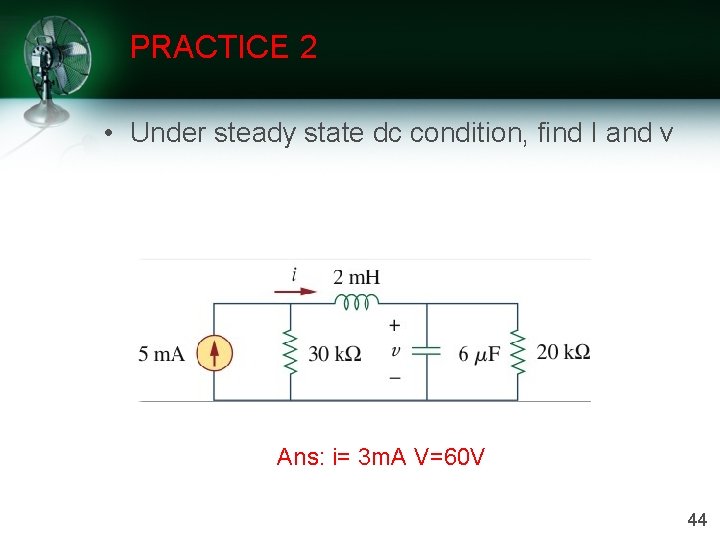
PRACTICE 2 • Under steady state dc condition, find I and v Ans: i= 3 m. A V=60 V 44

PRACTICE 3 • Determine Leq at terminal a-b Ans: Leq=7. 7778 m. H 45

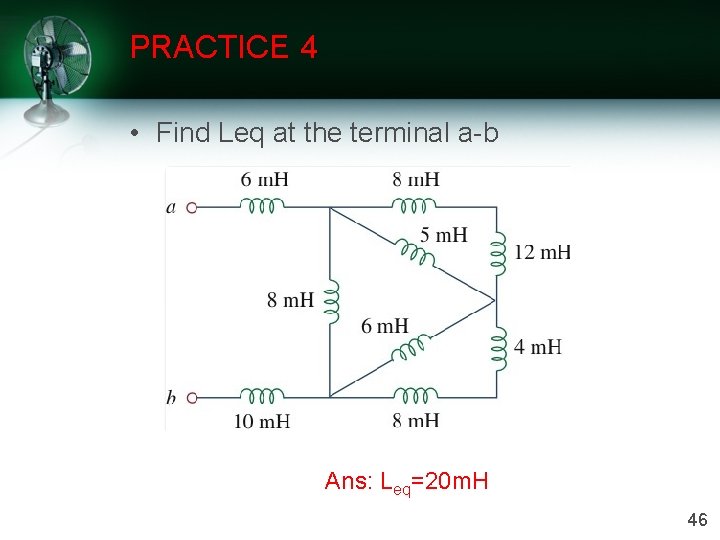
PRACTICE 4 • Find Leq at the terminal a-b Ans: Leq=20 m. H 46

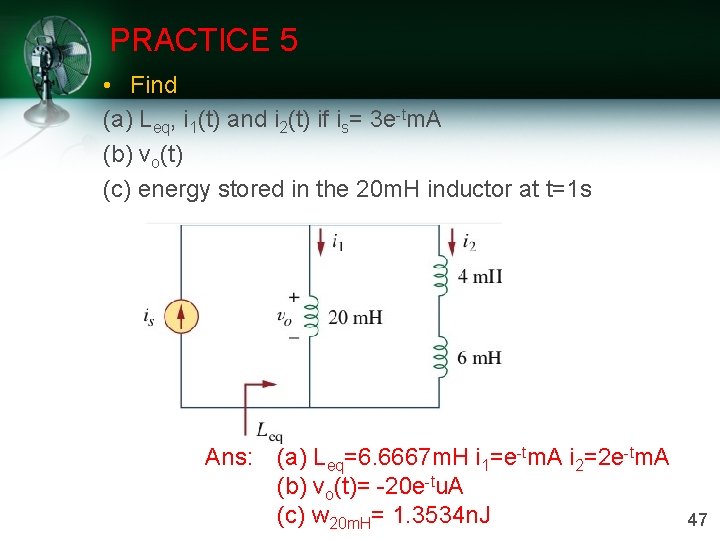
PRACTICE 5 • Find (a) Leq, i 1(t) and i 2(t) if is= 3 e-tm. A (b) vo(t) (c) energy stored in the 20 m. H inductor at t=1 s Ans: (a) Leq=6. 6667 m. H i 1=e-tm. A i 2=2 e-tm. A (b) vo(t)= -20 e-tu. A (c) w 20 m. H= 1. 3534 n. J 47