Electric Charge Fields and Potential AP PHYSICS UNIT

Electric Charge, Fields and Potential AP PHYSICS UNIT 8 GIANCOLI CH. 16 & 17

Electric Charges Use the PHET simulation to learn about electric charges and their effects.

Electric Charges Understanding of electricity originates within the atom. Why? Full of + and – charged particles Like charges attract and unlike charges repel Most material is electrically neutral same # of + & - charges Excess Charge Accumulation happens when two dissimilar materials rub against one another. One material gains electrons (- charge) the other loses electrons (+charge) Balloon and Sweater (balloon is - and the sweater is + ) Charge by induction Bringing a charged object close to a neutral object produces a temporary charge separation in the object.

Electroscopes Shows the presence of electric charge & can Metal plate and plastic(metal plate is + and the plastic is - ) Wooden stick and fur (wood is - and the fur is + ) Put a picture of an electroscope here

Electric Forces Finding the electric force between two charged particles is easy (with the help of Coulomb’s Law). But the problems get more difficult when more than two charges are involved. Strategy: 1. Calculate the individual forces on the charge from each additional charge 2. Add the force vectors to find the sum or net force.

Equilibrium Problems The place where a charge can be located for it to experience zero total force is called its equilibrium position. Strategy: 1. Use logic to find the general region of space for the equilibrium position. 2. Set the force due to one charge equal to the force due to a second charge.

Gravitational Fields A field represents the size and direction of the force felt by test particle. Size : acceleration of gravity (m/s 2) at a particular point is equal to the gravitational field strength (N/kg). Sea level = 9. 81 N/kg Everest = 9. 80 N/kg 1/10 of the distance to the Moon = 0. 27 N/kg Moon = 0. 0027 N/kg ½ of the distance to the center of the Earth = 39. 3 N/kg

Visual Representation of Earth’s Grav. Field Arrows / Vectors represent the size and direction of the gravitational field strength.

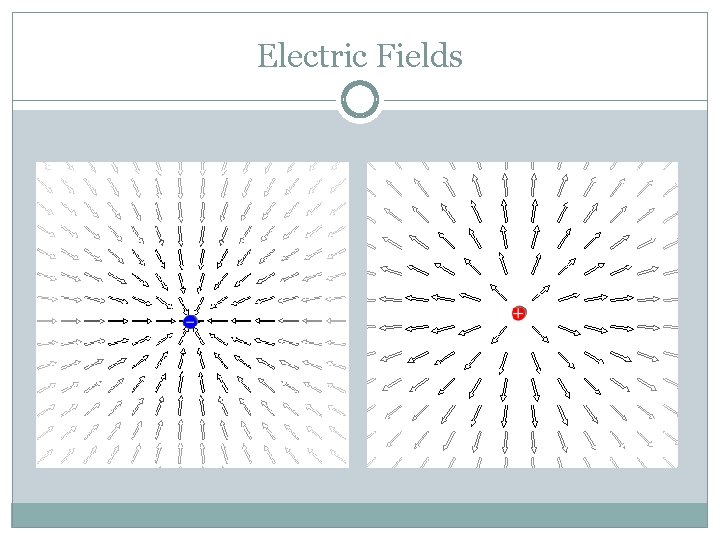
Electric Fields

Electric Fields A charged particle can be thought of as filling the space around it with an electric field waiting to exert forces on any test charge that enters into it. The Efield at any point in space is a vector whose magnitude is the force per unit charge that would act on the test charge, and whose direction is the same as the direction of force that would act on a positive point charge.

Ch. 17 Homework Assignment Read: 17. 1 -17. 5 and 17. 7 – 17. 9 Textbook (pg. 488) Questions: 1 -3, 5, 9 and 12 Problems: 1 -4, 12, 14, 15, 19, 20, 22, 31, 32, 34, 35, 44 and 47 Due: Monday (11. 07)

Electric Fields and Conductors + - Euniform - + + + - + - - A charge is induced on the surface of the conductor which creates an additional E-field same in size and opposite in direction to the external E-field, canceling it! “Shielding”

Shielding and Faraday Cages

Electric Fields and Conductors A charge inside a neutral spherical shell induces charge on its surfaces. The electric field exists even beyond the shell but not within the conductor itself. + + +Q + - - +

Electrical Energy and Potential Difference As a charge moves from point A to B in some path, the electric force does work on the charge. (W = Fd) Potential energy is important when dealing with charges moving in E-fields, but we also define a new quantity electric potential as the electric potential energy per unit charge. + - Euniform + A B + - Units: 1 V = 1 J/C

Electrical Energy and Potential Difference Electric potential depends on the charge outside the field, not on any charge that is inside the field. Because potential energy is dependent upon some arbitrary potential, only changes in potential energy are meaningful. Similarly, we will most always speak in terms of the change in potential (or potential difference) between two points. + - Euniform + A B + - Units: 1 V = 1 J/C

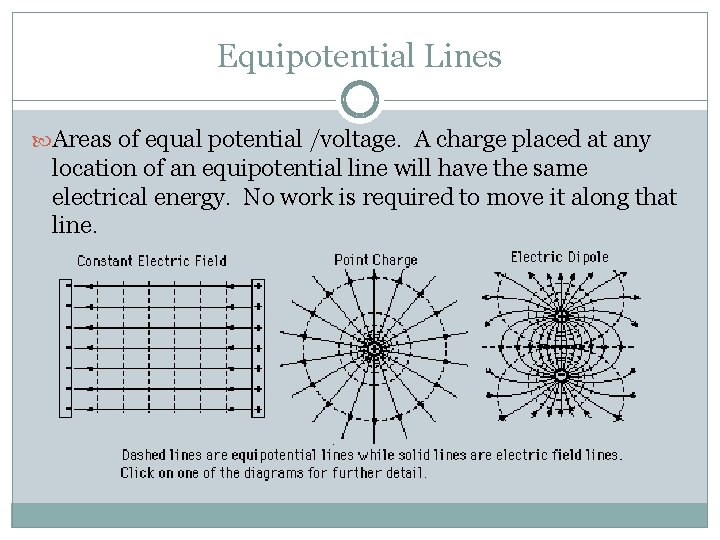
Equipotential Lines Areas of equal potential /voltage. A charge placed at any location of an equipotential line will have the same electrical energy. No work is required to move it along that line.

Gravitational Analogy Think about a rock falling from the top of a cliff. The amount of work that the gravitational field will do on the rock as it falls depends on how much its energy changes during the fall – which really depends on the height of the cliff and the mass of the rock. A large rock and a small rock can be at the same height and therefore have the same gravitational potential (J/kg), but the larger rock has the greater energy because of its larger mass. M 2 M H

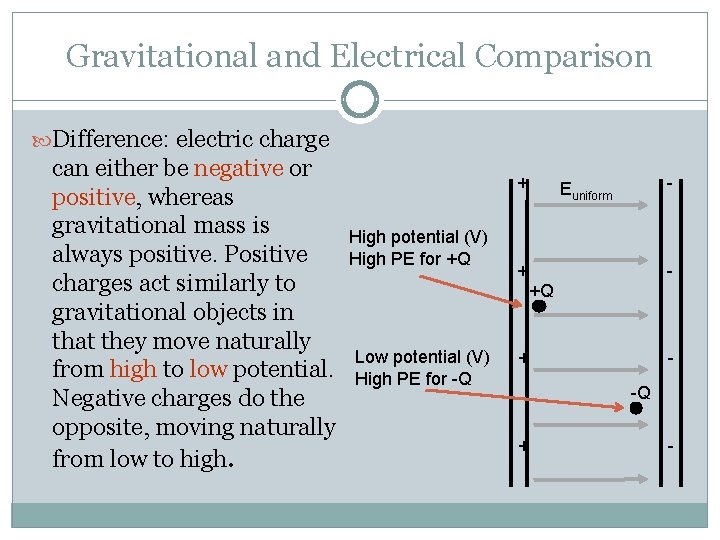
Gravitational and Electrical Comparison Both charges and both masses have the same potential (J/C or J/kg), but the larger charge and mass have more energy because of their size. + Euniform 2 M M + 2 Q + + Q H - -

Gravitational and Electrical Comparison The work done by the E-field in moving the charge from one charged plate to the other depends on both the potential difference (like the height of the cliff), and the charge placed in the field (like the mass of the rock). + Euniform 2 M M + 2 Q + + Q H - -

Gravitational and Electrical Comparison Difference: electric charge can either be negative or positive, whereas gravitational mass is always positive. Positive charges act similarly to gravitational objects in that they move naturally from high to low potential. Negative charges do the opposite, moving naturally from low to high. + High potential (V) High PE for +Q - Euniform + +Q Low potential (V) High PE for -Q + -

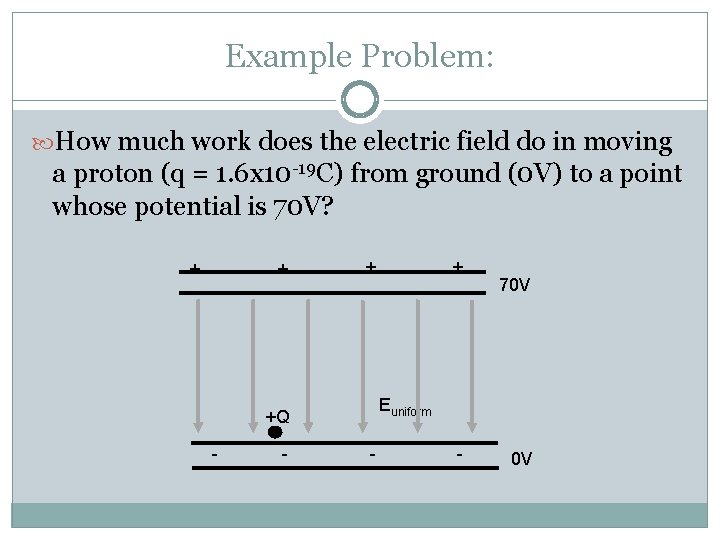
Example Problem: How much work does the electric field do in moving + + a proton (q = 1. 6 x 10 -19 C) from ground (0 V) to a point whose potential is 70 V? 70 V Euniform +Q - - 0 V

Potential and E-Fields Derivation… Units: 1 V = 1 J/C

Example Problem A +5 C charge moves 3 cm parallel to a uniform electric field of magnitude 300 V/m. What potential difference did the charge move through? Potential Difference (V) = 9 volts

The Electron Volt The S. I. unit of work or energy, the Joule, is a very large unit if you dealing with energies of very small particles (like electrons, for example). So we define a new unit of energy, the electron volt, as the energy acquired by an electron (or similarly charged particle) as a result of moving through a potential difference of 1 Volt.

Potential Due to Point Charges You can calculate the potential at a distance r from a single point charge. (This is similar to calculating the E-field created by a point charge) Because only a difference in potential is meaningful, we must define a location at which potential equals zero. For a point charge at some point in space, we say V = 0 at infinity. Potential is a scalar quantity, but its sign still matters.

Example Problem Three charges are arranged as shown in the figure. Find the electric potential at the position of the 3 n. C charge. Then find how much energy would be expended in moving the 3 n. C charge to infinity. 2 n. C + 50 cm 1. 5 m - -5 n. C 1. 58 m + 3 n. C Potential Difference (V) = 64 V, Energy = 1. 92 x 10 -7 J

Capacitance Capacitors are devices used in circuits to store charge and energy. They usually consist of two parallel metal plates separated by some distance. When each plate is hooked up to a terminal of a battery, electrons are pulled off one of the plates and deposited on the other plate. It is found that the amount of charge acquired by each plate is proportional to the magnitude of the potential difference between them. Capacitance is the constant of proportionality, relating charge to potential difference.

Various Capacitors

Capacitors The capacitance of a capacitor depends on the geometric arrangement of the plates (size, shape and relative position). For a parallel plate capacitor: εo = permitivity of free space A = area of plates d = plate separation distance

Example Problem Each plate of a parallel-plate capacitor has an area of 4. 0 cm 2 and the plates are separated by a distance of 2. 3 mm. If it stores a charge of 300 p. C, what is the potential difference across the plates of the capacitor? Potential Difference (V) = 195 volts

Dielectrics The previous expression for capacitance based on the geometric arrangement of the plates assumes that the space between the plates is filled with air or a vacuum. In most capacitors there is actually a sheet of material, such as paper or plastic, called a dielectric between the plates. The purpose of this dielectric is that dielectrics do not break down (allow electric charge to flow) as easily as air. So the plates may be closer together, and the voltage across the capacitor may be increased when using a dielectric.

Capacitance with Dielectrics Material Dielectric Constant (K) Vacuum 1. 0000 Air (1 atm) 1. 0006 Vinyl (plastic) 2 -4 Paper 3. 7 Oil 4 Glass, Pyrex 5 Strontium titanate 300 Table on pg. 483 K = dielectric constant εo = permitivity of free space A = area of plates d = plate separation distance

Example Problem What is the capacitance of two plates of area 25 cm 2 that are separated by 8 mm of paper? Capacitance = 1. 02 x 10 -11 F or 10. 2 p. F

Storing Electric Energy The energy stored in a capacitor is equal to the work needed to move all of the charge from one plate to another, across the potential difference (V) between the plates. Ex: How much energy is stored in a 2200 p. F capacitor that is connected across a 650 V source? Uc = 4. 6 x 10 -4 J