ELEC 7770 Advanced VLSI Design Spring 2008 Constraint

ELEC 7770 Advanced VLSI Design Spring 2008 Constraint Graph and Performance Optimization Vishwani D. Agrawal James J. Danaher Professor ECE Department, Auburn University Auburn, AL 36849 vagrawal@eng. auburn. edu http: //www. eng. auburn. edu/~vagrawal/COURSE/E 7770_Spr 08/course. html Spring 08, Mar 4, 6 ELEC 7770: Advanced VLSI Design (Agrawal) 1

Retiming Theorem § Given a network G(V, E, W) and a cycle time T, (r 1, . . . ) is a feasible retiming if and only if: § ri – rj ≤ wij for all edges (vi, vj) ε E § ri – rj ≤ W(vi, vj) – 1 for all node-pairs vi, vj such that D(vi, vj) > T Where, W(vi, vj) is the minimum weight path between vi and vj D(vi, vj) is the maximum delay among all minimum weight paths between vi and vj Spring 08, Mar 4, 6 ELEC 7770: Advanced VLSI Design (Agrawal) 2

Timing Optimization § Find the clock period (T) by path analysis. § Set clock period to T/2 and find a feasible § § retiming. If feasible, further reduce the clock period to half. If not feasible, increase clock period. Do a binary search for optimum clock period. Retime the circuit. Spring 08, Mar 4, 6 ELEC 7770: Advanced VLSI Design (Agrawal) 3

Representing a Constraint ri – rj ≤ wij rj Spring 08, Mar 4, 6 or – wij rj ≥ ri – wij ri ELEC 7770: Advanced VLSI Design (Agrawal) 4

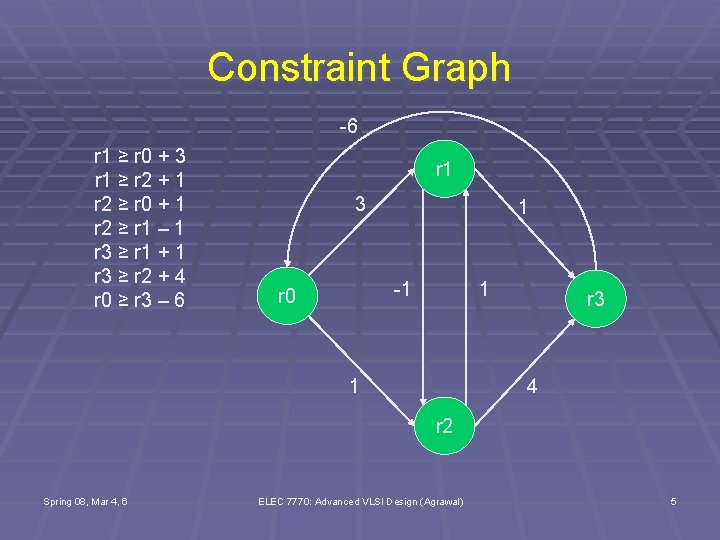
Constraint Graph -6 r 1 ≥ r 0 + 3 r 1 ≥ r 2 + 1 r 2 ≥ r 0 + 1 r 2 ≥ r 1 – 1 r 3 ≥ r 1 + 1 r 3 ≥ r 2 + 4 r 0 ≥ r 3 – 6 r 1 3 1 -1 r 0 1 1 r 3 4 r 2 Spring 08, Mar 4, 6 ELEC 7770: Advanced VLSI Design (Agrawal) 5

Feasibility Condition § A set of values for variables can be found if and § only if the constraint graph has no positive cycles. This is also the condition for the solvability of the longest path problem, which provides a solution to the set of constraints. Spring 08, Mar 4, 6 ELEC 7770: Advanced VLSI Design (Agrawal) 6

Example: Infeasible Constraints x 2 x 1 ≥ x 2 + 6 x 2 ≥ x 1 – 3 6 x 1 3 x 2 ≥ x 1 – 3 x 2 -3 Positive cycle mean no longest path can be found. Spring 08, Mar 4, 6 x 1 ≥ x 2 + 6 0 3 ELEC 7770: Advanced VLSI Design (Agrawal) 6 x 1 7

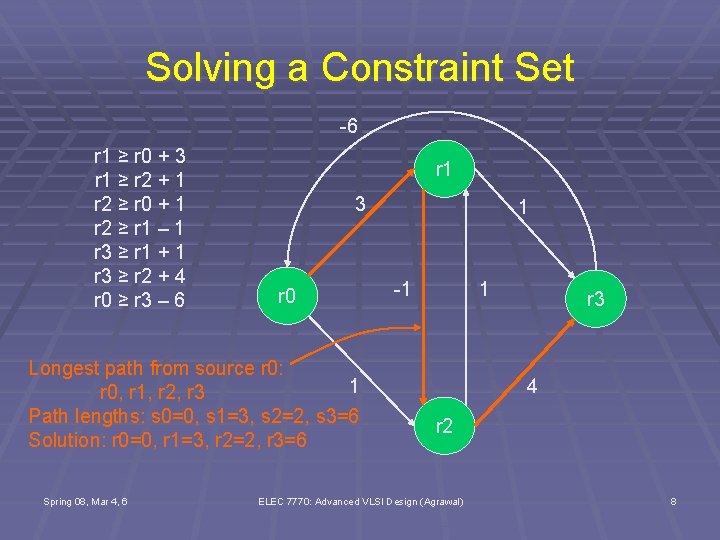
Solving a Constraint Set -6 r 1 ≥ r 0 + 3 r 1 ≥ r 2 + 1 r 2 ≥ r 0 + 1 r 2 ≥ r 1 – 1 r 3 ≥ r 1 + 1 r 3 ≥ r 2 + 4 r 0 ≥ r 3 – 6 r 1 3 r 0 Longest path from source r 0: 1 r 0, r 1, r 2, r 3 Path lengths: s 0=0, s 1=3, s 2=2, s 3=6 Solution: r 0=0, r 1=3, r 2=2, r 3=6 Spring 08, Mar 4, 6 1 -1 1 r 3 4 r 2 ELEC 7770: Advanced VLSI Design (Agrawal) 8

The General Path Problem § Find the shortest (or longest) path in a graph § from a source vertex to all other vertices. Graph has vertices and directed edges: § Edge weights can be positive or negative § Graph can be cyclic § Single source vertex – a vertex with 0 in-degree (not a necessary condition) § Inconsistent problems § Negative weight cycles for shortest path § Positive weight cycles for longest path Spring 08, Mar 4, 6 ELEC 7770: Advanced VLSI Design (Agrawal) 9

Dijkstra’s Shortest Path Algorithm § Greedy algorithm. § Applies to directed acyclic graphs (DAG) with positive § § edge weights. Computational complexity O(|E| + |V| log |V|) ≤ O(n 2) References: § A. Aho, J. Hopcroft and J. Ullman, Data Structures and Algorithms, Reading, Massachusetts: Addison-Wesley, 1983. § T. Cormen, C. Leiserson and R. Rivest, Introduction to Algorithms, New York: Mc. Graw-Hill, 1990. Spring 08, Mar 4, 6 ELEC 7770: Advanced VLSI Design (Agrawal) 10

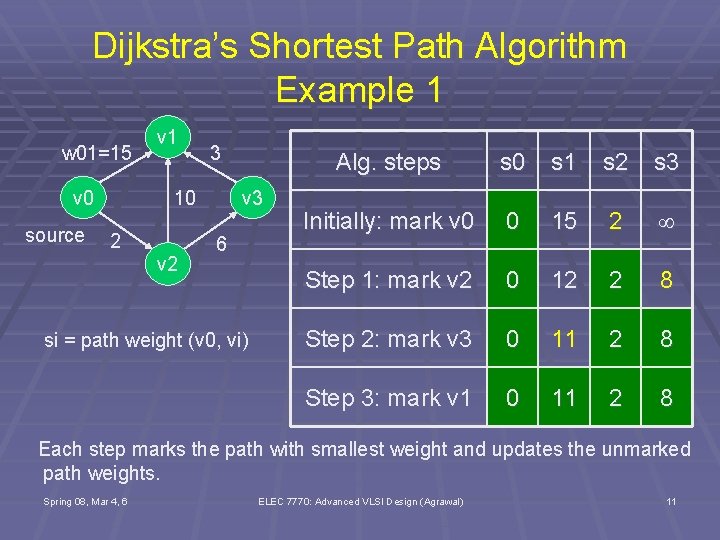
Dijkstra’s Shortest Path Algorithm Example 1 w 01=15 v 0 source v 1 3 v 3 10 2 v 2 6 si = path weight (v 0, vi) Alg. steps s 0 s 1 s 2 s 3 Initially: mark v 0 0 15 2 Step 1: mark v 2 0 12 2 8 Step 2: mark v 3 0 11 2 8 Step 3: mark v 1 0 11 2 8 Each step marks the path with smallest weight and updates the unmarked path weights. Spring 08, Mar 4, 6 ELEC 7770: Advanced VLSI Design (Agrawal) 11

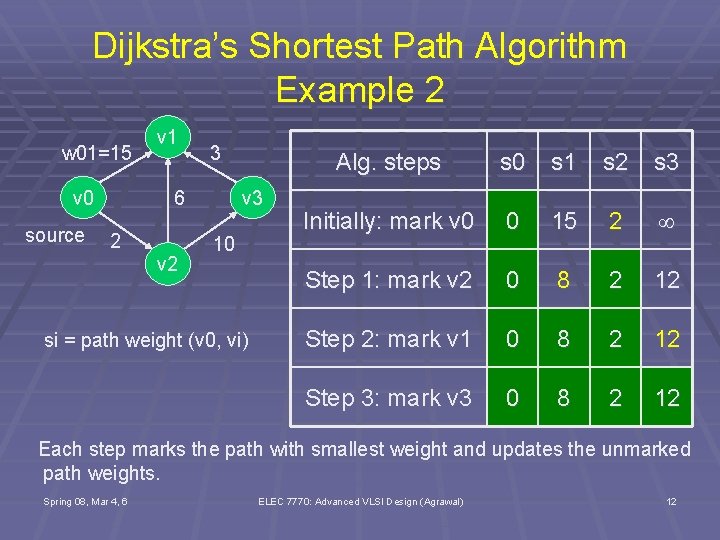
Dijkstra’s Shortest Path Algorithm Example 2 w 01=15 v 0 source v 1 3 v 3 6 2 v 2 10 si = path weight (v 0, vi) Alg. steps s 0 s 1 s 2 s 3 Initially: mark v 0 0 15 2 Step 1: mark v 2 0 8 2 12 Step 2: mark v 1 0 8 2 12 Step 3: mark v 3 0 8 2 12 Each step marks the path with smallest weight and updates the unmarked path weights. Spring 08, Mar 4, 6 ELEC 7770: Advanced VLSI Design (Agrawal) 12

Dijkstra’s Algorithm, G(V, E, W) s 0(1) = 0 for ( i = 1 to n ) initialize source initialize path weights, n=|V| – 1 si(1) = w 0 i repeat { Select an unmarked vertex vq such that sq is minimal Mark vq foreach ( unmarked vertex vi ) si = min { si, sq + wqi } } until (all vertices are marked) Spring 08, Mar 4, 6 ELEC 7770: Advanced VLSI Design (Agrawal) 13

Try Dijkstra’s Algorithm for Your Graph http: //www. dgp. toronto. edu/people/James. Stewart/270/9798 s/Laffra/Dijkstra. Applet. html Spring 08, Mar 4, 6 ELEC 7770: Advanced VLSI Design (Agrawal) 14

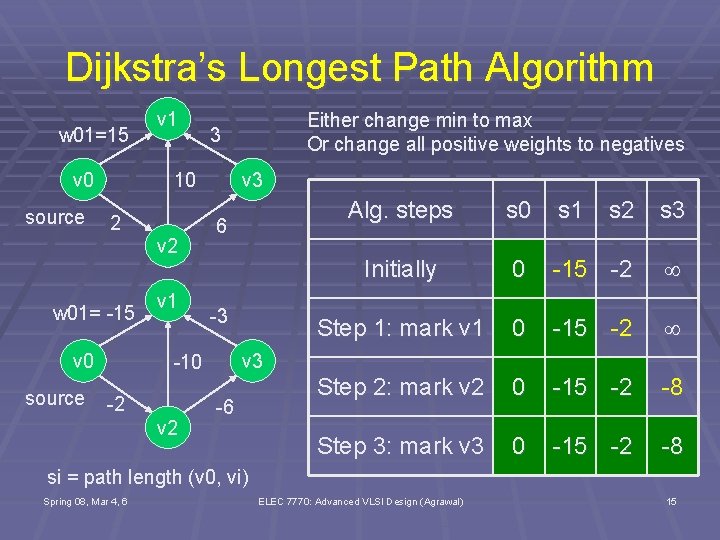
Dijkstra’s Longest Path Algorithm w 01=15 v 0 source v 1 v 2 w 01= -15 v 0 source 3 v 3 10 2 v 1 6 -3 v 2 Alg. steps s 0 s 1 s 2 s 3 Initially 0 -15 -2 Step 1: mark v 1 0 -15 -2 Step 2: mark v 2 0 -15 -2 -8 Step 3: mark v 3 0 -15 -2 -8 v 3 -10 -2 Either change min to max Or change all positive weights to negatives -6 si = path length (v 0, vi) Spring 08, Mar 4, 6 ELEC 7770: Advanced VLSI Design (Agrawal) 15

Dijkstra’s Alg. Does Not Work for Cycles, Mixed Weights -2 w 01=15 v 0 source v 1 3 v 3 5 2 v 2 4 si = path weight (v 0, vi) Alg. steps s 0 s 1 s 2 s 3 Initially: mark v 0 0 15 2 Step 1: mark v 2 0 7 2 6 Step 2: mark v 3 0 7 2 6 Step 3: mark v 1 0 7 2 6? Algorithm stops because all vertices are marked. But, there exists a v 0 to v 3 path of length 5 Spring 08, Mar 4, 6 ELEC 7770: Advanced VLSI Design (Agrawal) 16

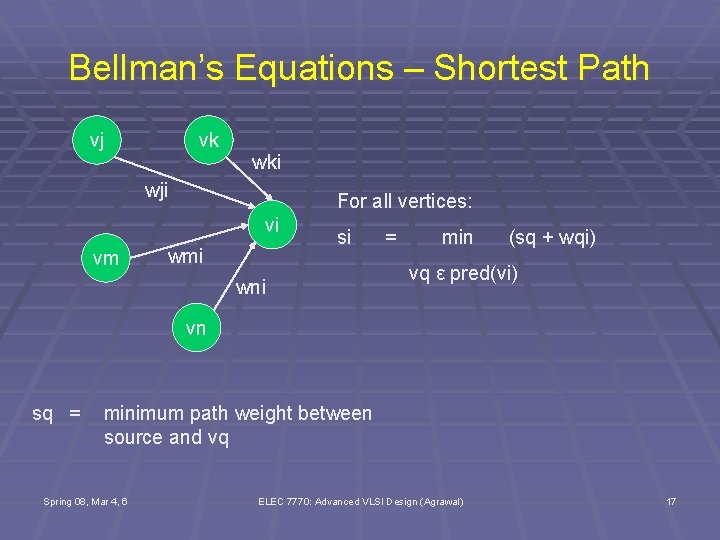
Bellman’s Equations – Shortest Path vj vk wki wji For all vertices: vi vm wmi si wni = min (sq + wqi) vq ε pred(vi) vn sq = minimum path weight between source and vq Spring 08, Mar 4, 6 ELEC 7770: Advanced VLSI Design (Agrawal) 17

Bellman-Ford Algorithm, G(V, E, W) Bellman-Ford { s 0(1) = 0 for ( i = 1 to n ) initialize source initialize path weights, n = |V| – 1 si(1) = w 0 i for ( j = 1 to n ) n iterations for ( i = 1 to n ) si(j+1) = min { si(j), sk(j) + wkj } vk ε pred(vi) } if ( si(j+1) == si(j) i ) return (true) } return (false) Spring 08, Mar 4, 6 Complexity = O(|V||E|) ≤ O(n 3) ELEC 7770: Advanced VLSI Design (Agrawal) 18

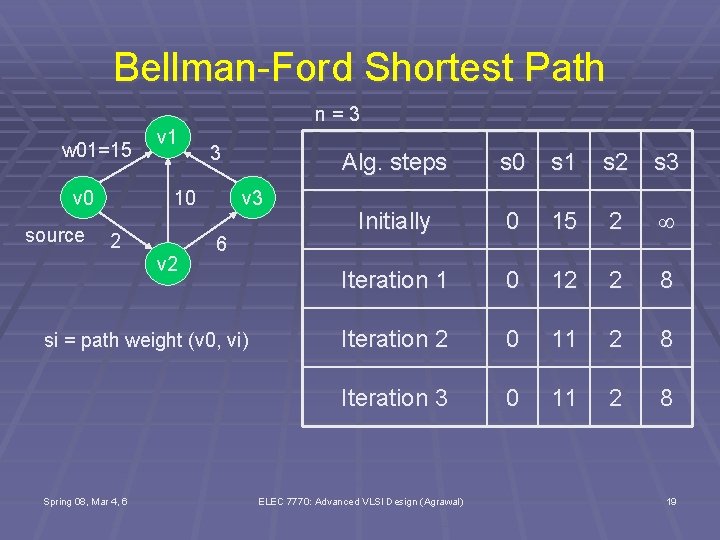
Bellman-Ford Shortest Path n=3 w 01=15 v 0 source v 1 3 v 3 10 2 v 2 6 si = path weight (v 0, vi) Spring 08, Mar 4, 6 Alg. steps s 0 s 1 s 2 s 3 Initially 0 15 2 Iteration 1 0 12 2 8 Iteration 2 0 11 2 8 Iteration 3 0 11 2 8 ELEC 7770: Advanced VLSI Design (Agrawal) 19

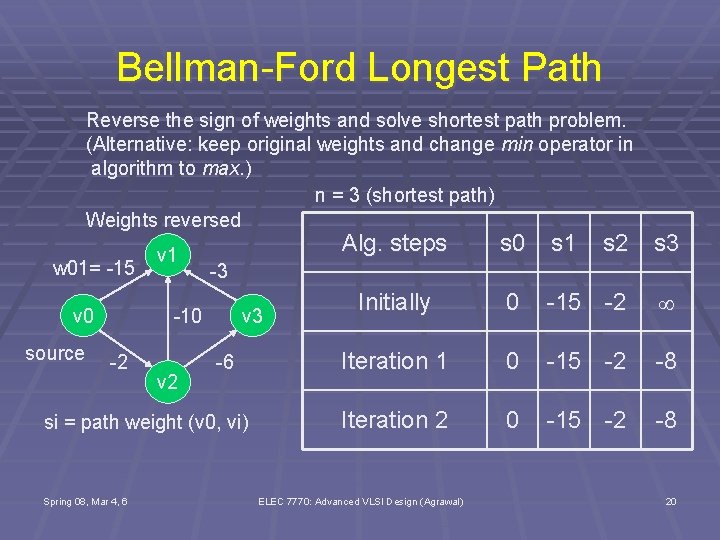
Bellman-Ford Longest Path Reverse the sign of weights and solve shortest path problem. (Alternative: keep original weights and change min operator in algorithm to max. ) n = 3 (shortest path) Weights reversed w 01= -15 v 0 source v 1 v 2 v 3 -6 si = path weight (v 0, vi) Spring 08, Mar 4, 6 s 0 s 1 s 2 s 3 Initially 0 -15 -2 Iteration 1 0 -15 -2 -8 Iteration 2 0 -15 -2 -8 -3 -10 -2 Alg. steps ELEC 7770: Advanced VLSI Design (Agrawal) 20

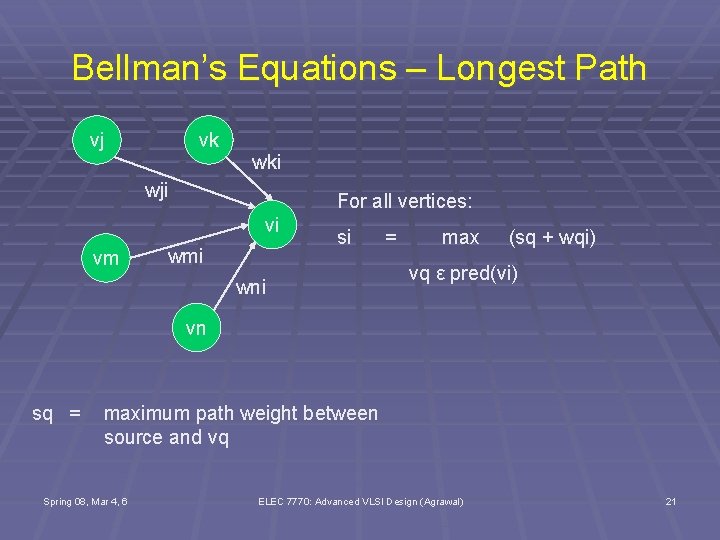
Bellman’s Equations – Longest Path vj vk wki wji For all vertices: vi vm wmi si wni = max (sq + wqi) vq ε pred(vi) vn sq = maximum path weight between source and vq Spring 08, Mar 4, 6 ELEC 7770: Advanced VLSI Design (Agrawal) 21

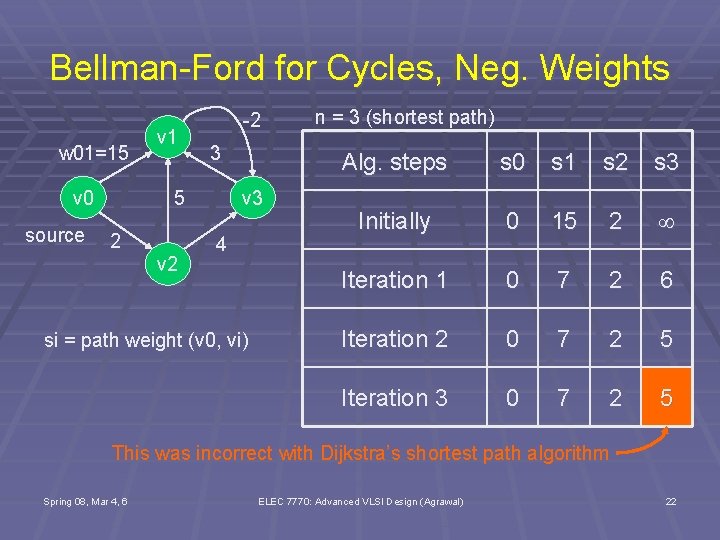
Bellman-Ford for Cycles, Neg. Weights w 01=15 v 0 source v 1 -2 3 v 3 5 2 v 2 4 si = path weight (v 0, vi) n = 3 (shortest path) Alg. steps s 0 s 1 s 2 s 3 Initially 0 15 2 Iteration 1 0 7 2 6 Iteration 2 0 7 2 5 Iteration 3 0 7 2 5 This was incorrect with Dijkstra’s shortest path algorithm Spring 08, Mar 4, 6 ELEC 7770: Advanced VLSI Design (Agrawal) 22

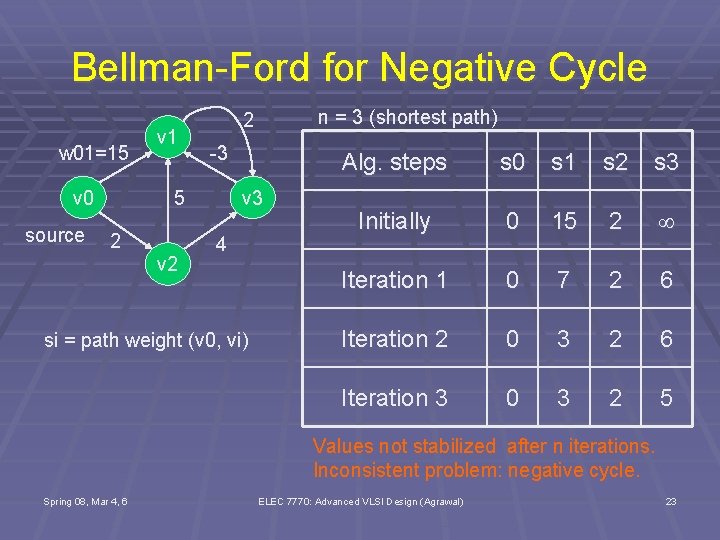
Bellman-Ford for Negative Cycle w 01=15 v 0 source v 1 -3 v 3 5 2 v 2 n = 3 (shortest path) 2 4 si = path weight (v 0, vi) Alg. steps s 0 s 1 s 2 s 3 Initially 0 15 2 Iteration 1 0 7 2 6 Iteration 2 0 3 2 6 Iteration 3 0 3 2 5 Values not stabilized after n iterations. Inconsistent problem: negative cycle. Spring 08, Mar 4, 6 ELEC 7770: Advanced VLSI Design (Agrawal) 23

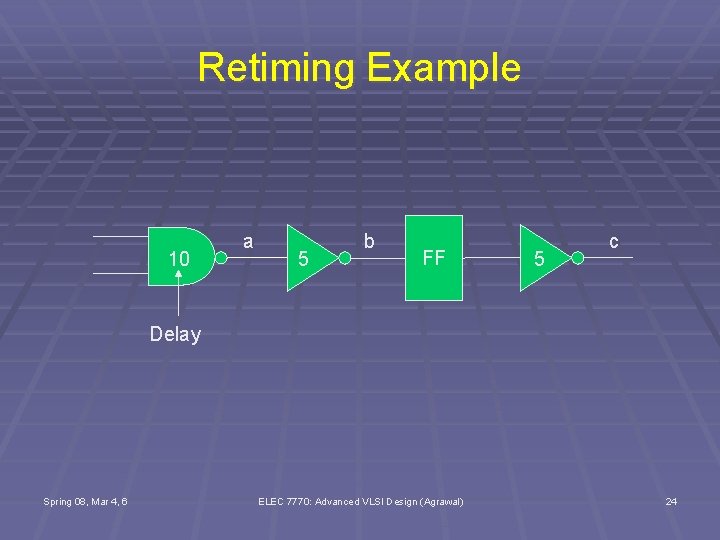
Retiming Example 10 a 5 b FF 5 c Delay Spring 08, Mar 4, 6 ELEC 7770: Advanced VLSI Design (Agrawal) 24

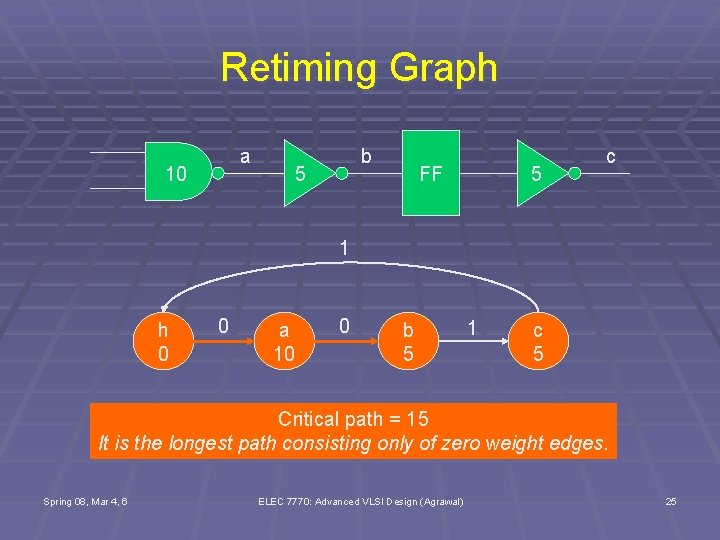
Retiming Graph a 10 b 5 FF 5 c 1 h 0 0 a 10 0 b 5 1 c 5 Critical path = 15 It is the longest path consisting only of zero weight edges. Spring 08, Mar 4, 6 ELEC 7770: Advanced VLSI Design (Agrawal) 25

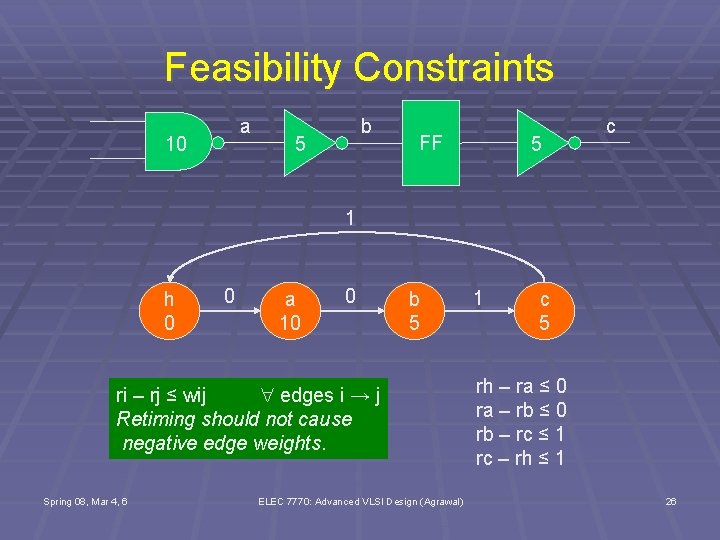
Feasibility Constraints a 10 b 5 FF 5 c 1 h 0 0 a 10 0 b 5 ri – rj ≤ wij edges i → j Retiming should not cause negative edge weights. Spring 08, Mar 4, 6 ELEC 7770: Advanced VLSI Design (Agrawal) 1 c 5 rh – ra ≤ 0 ra – rb ≤ 0 rb – rc ≤ 1 rc – rh ≤ 1 26

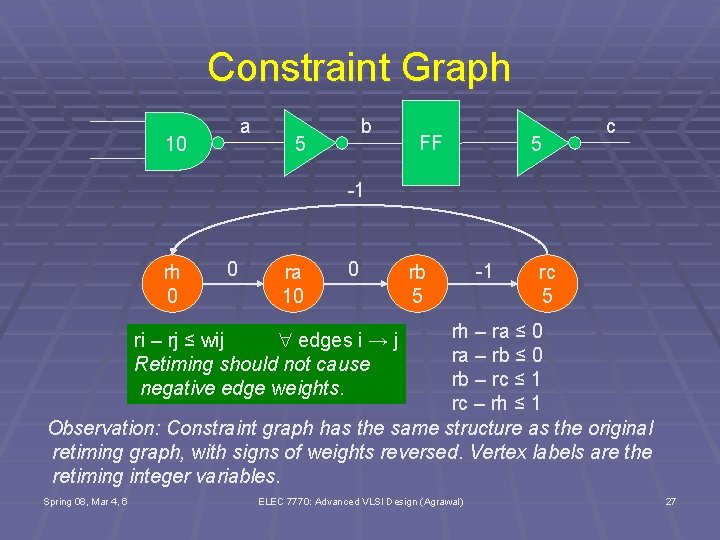
Constraint Graph a 10 b 5 FF 5 c -1 rh 0 0 ra 10 0 rb 5 -1 rc 5 rh – ra ≤ 0 ra – rb ≤ 0 rb – rc ≤ 1 rc – rh ≤ 1 Observation: Constraint graph has the same structure as the original retiming graph, with signs of weights reversed. Vertex labels are the retiming integer variables. ri – rj ≤ wij edges i → j Retiming should not cause negative edge weights. Spring 08, Mar 4, 6 ELEC 7770: Advanced VLSI Design (Agrawal) 27

Max Delay for Min Weight Paths 1 h 0 0 a 10 0 b 5 1 c 5 T = 15 W(h, a) = 0 W(h, b) = 0 W(h, c) = 1 W(a, b) = 0 W(a, c) = 1 W(a, h) = 2 Spring 08, Mar 4, 6 D(h, a) = 10 D(h, b) = 15 D(h, c) = 20 D(a, b) = 15 D(a, c) = 20 D(a, h) = 20 W(b, c) = 1 W(b, h) = 2 W(b, a) = 2 W(c, h) = 1 W(c, a) = 1 W(c, b) = 1 ELEC 7770: Advanced VLSI Design (Agrawal) D(b, c) = 10 D(b, h) = 10 D(b, a) = 20 D(c, h) = 5 D(c, a) = 15 D(c, b) = 20 28

Timing Optimization, T = 7. 5? -1 rh 0 0 ra 10 ri – rj ≤ W(I, j) – 1 W(h, a) = 0 W(h, b) = 0 W(h, c) = 1 W(a, b) = 0 W(a, c) = 1 W(a, h) = 2 Spring 08, Mar 4, 6 0 Constraint graph (feasibility) rb 5 -1 rc 5 paths (i, j) such that D(i, j) > 7. 5 D(h, a) = 10 D(h, b) = 15 D(h, c) = 20 D(a, b) = 15 D(a, c) = 20 D(a, h) = 20 W(b, c) = 1 W(b, h) = 2 W(b, a) = 2 W(c, h) = 1 W(c, a) = 1 W(c, b) = 1 ELEC 7770: Advanced VLSI Design (Agrawal) D(b, c) = 10 D(b, h) = 10 D(b, a) = 20 D(c, h) = 5 D(c, a) = 15 D(c, b) = 20 29

Timing Optimization, T = 7. 5? -1 0 -1 -1 W(h, a) = 0 W(h, b) = 0 W(h, c) = 1 W(a, b) = 0 W(a, c) = 1 W(a, h) = 2 Spring 08, Mar 4, 6 1 1 1 rh 0 Positive cycle No solution 0 0 ra 10 -1 0 rb 5 -1 0 rc 5 0 0 D(h, a) = 10 D(h, b) = 15 D(h, c) = 20 D(a, b) = 15 D(a, c) = 20 D(a, h) = 20 W(b, c) = 1 W(b, h) = 2 W(b, a) = 2 W(c, h) = 1 W(c, a) = 1 W(c, b) = 1 ELEC 7770: Advanced VLSI Design (Agrawal) D(b, c) = 10 D(b, h) = 10 D(b, a) = 20 D(c, h) = 5 D(c, a) = 15 D(c, b) = 20 30

Timing Optimization, T = 11. 25? -1 1 1 rh 0 0 -1 0 ra 10 -1 0 W(h, a) = 0 W(h, b) = 0 W(h, c) = 1 W(a, b) = 0 W(a, c) = 1 W(a, h) = 2 Spring 08, Mar 4, 6 0 D(h, a) = 10 D(h, b) = 15 D(h, c) = 20 D(a, b) = 15 D(a, c) = 20 D(a, h) = 20 0 rb 5 -1 rc 5 rh = 0 rb = 1 rc = 0 ra = 0 0 W(b, c) = 1 W(b, h) = 2 W(b, a) = 2 W(c, h) = 1 W(c, a) = 1 W(c, b) = 1 ELEC 7770: Advanced VLSI Design (Agrawal) D(b, c) = 10 D(b, h) = 10 D(b, a) = 20 D(c, h) = 5 D(c, a) = 15 D(c, b) = 20 31

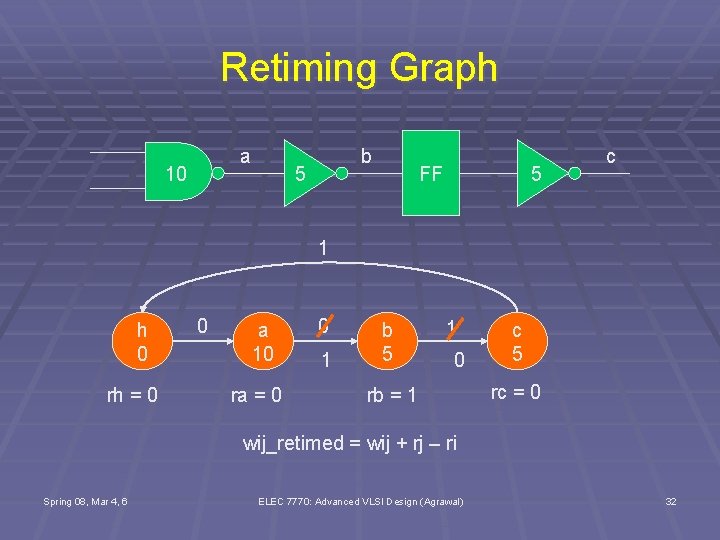
Retiming Graph a 10 b 5 FF 5 c 1 h 0 rh = 0 0 a 10 ra = 0 0 1 b 5 1 0 rb = 1 c 5 rc = 0 wij_retimed = wij + rj – ri Spring 08, Mar 4, 6 ELEC 7770: Advanced VLSI Design (Agrawal) 32

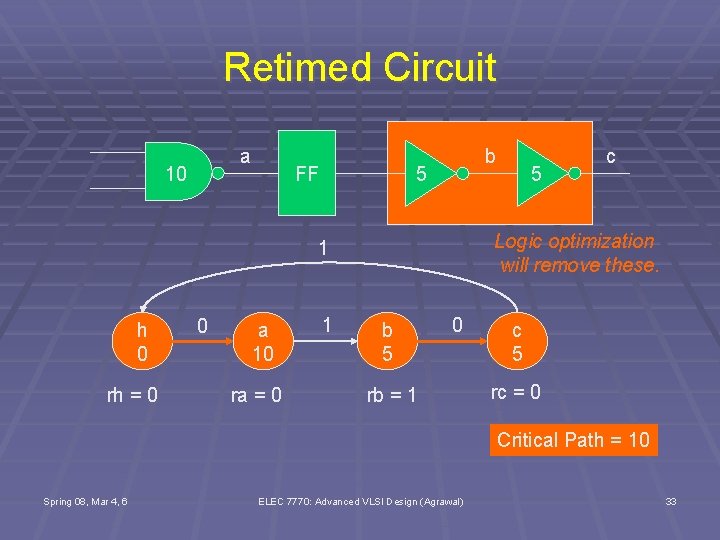
Retimed Circuit a 10 FF b 5 Logic optimization will remove these. 1 h 0 rh = 0 0 a 10 ra = 0 1 5 c b 5 0 rb = 1 c 5 rc = 0 Critical Path = 10 Spring 08, Mar 4, 6 ELEC 7770: Advanced VLSI Design (Agrawal) 33