ELEC 7770 Advanced VLSI Design Spring 2008 Clock









- Slides: 16

ELEC 7770 Advanced VLSI Design Spring 2008 Clock Skew Problem Vishwani D. Agrawal James J. Danaher Professor ECE Department, Auburn University Auburn, AL 36849 vagrawal@eng. auburn. edu http: //www. eng. auburn. edu/~vagrawal/COURSE/E 7770_Spr 08/course. html Spring 08, Feb 26 ELEC 7770: Advanced VLSI Design (Agrawal) 1

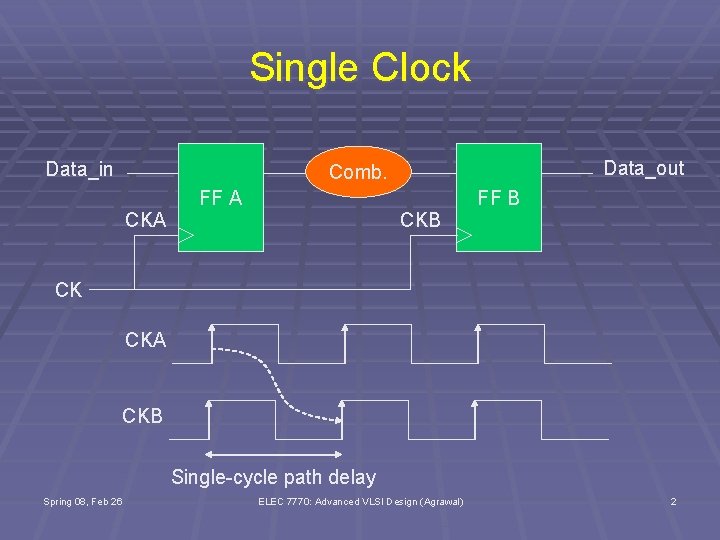
Single Clock Data_in Data_out Comb. CKA FF A CKB FF B CK CKA CKB Single-cycle path delay Spring 08, Feb 26 ELEC 7770: Advanced VLSI Design (Agrawal) 2

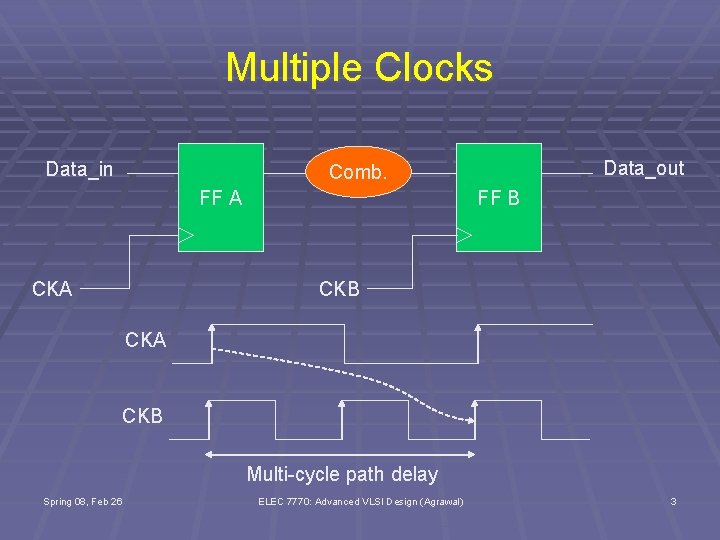
Multiple Clocks Data_in Data_out Comb. FF A CKA FF B CKA CKB Multi-cycle path delay Spring 08, Feb 26 ELEC 7770: Advanced VLSI Design (Agrawal) 3

Clock Skew § Skew is the time delay of clock signal at a flip§ § flop with respect to some time reference. For a given layout each flip-flop has a skew, measured with respect to the a common reference. Skews of flip-flops separated by combinational paths affect the short-path and long-path constraints. Spring 08, Feb 26 ELEC 7770: Advanced VLSI Design (Agrawal) 4

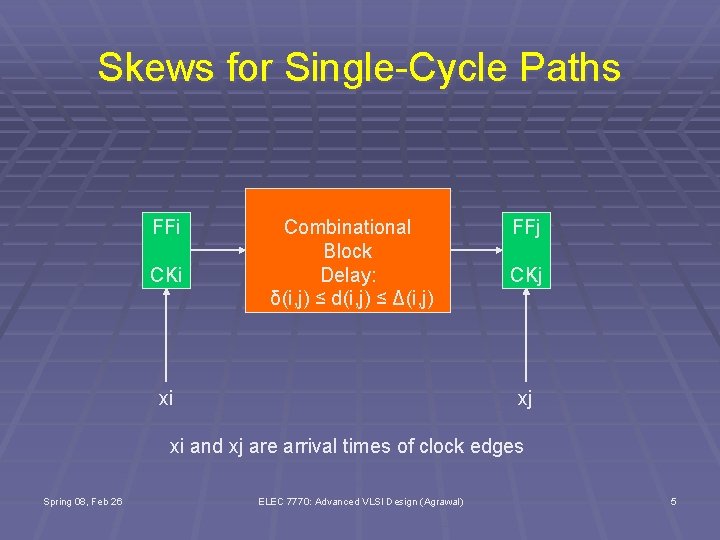
Skews for Single-Cycle Paths FFi CKi Combinational Block Delay: δ(i, j) ≤ d(i, j) ≤ Δ(i, j) xi FFj CKj xj xi and xj are arrival times of clock edges Spring 08, Feb 26 ELEC 7770: Advanced VLSI Design (Agrawal) 5

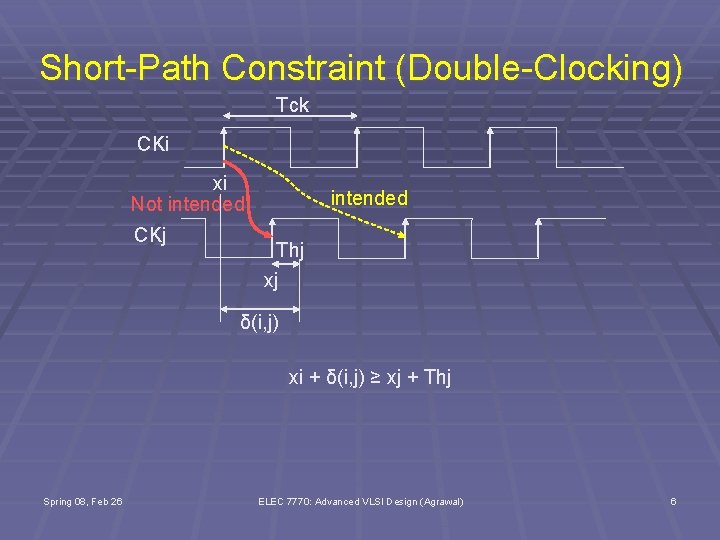
Short-Path Constraint (Double-Clocking) Tck CKi xi Not intended CKj intended Thj xj δ(i, j) xi + δ(i, j) ≥ xj + Thj Spring 08, Feb 26 ELEC 7770: Advanced VLSI Design (Agrawal) 6

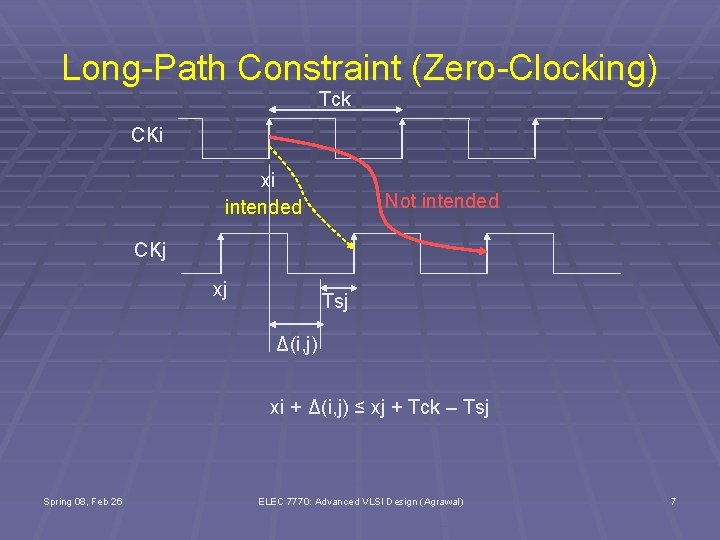
Long-Path Constraint (Zero-Clocking) Tck CKi xi intended Not intended CKj xj Tsj Δ(i, j) xi + Δ(i, j) ≤ xj + Tck – Tsj Spring 08, Feb 26 ELEC 7770: Advanced VLSI Design (Agrawal) 7

Maximum Clock Frequency Linear program: Minimize Tck Subject to: For all flip-flop pairs (i, j), xi + δ(i, j) ≥ xj + Thj xi + Δ(i, j) ≤ xj + Tck – Tsj Spring 08, Feb 26 ELEC 7770: Advanced VLSI Design (Agrawal) 8

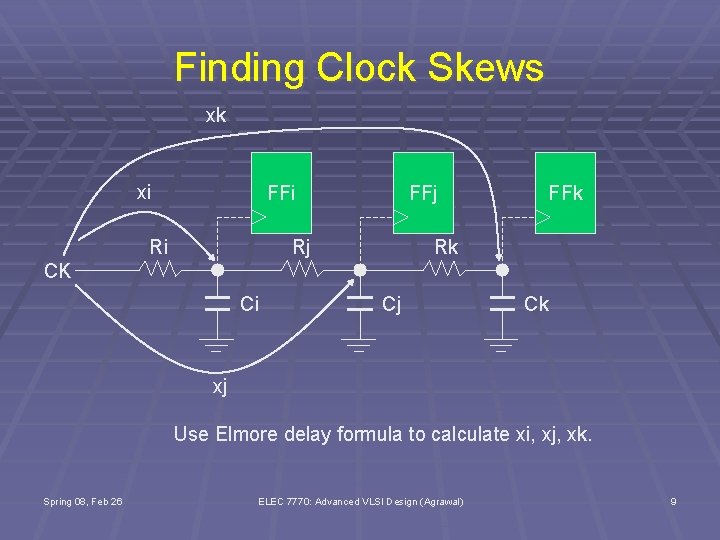
Finding Clock Skews xk xi FFi Ri FFj Rj FFk Rk CK Ci Cj Ck xj Use Elmore delay formula to calculate xi, xj, xk. Spring 08, Feb 26 ELEC 7770: Advanced VLSI Design (Agrawal) 9

Interconnect Delay: Elmore Delay Model § W. Elmore, “The Transient Response of Damped Linear Networks with Particular Regard to Wideband Amplifiers, ” J. Appl. Phys. , vol. 19, no. 1, pp. 55 -63, Jan. 1948. CK Shared resistance: Rii = Ri Rij = Rji = Ri Rik = Rki = Ri Rjj = Ri + Rj Rjk = Rkj = Ri + Rj Rkk = Ri + Rj + Rk Spring 08, Feb 26 Ri i Rj Ci Rk j Cj ELEC 7770: Advanced VLSI Design (Agrawal) k Ck 10

Elmore Delay Calculation Delay at node k, xk = 0. 69 (Ci × Rik + Cj × Rjk + Ck × Rkk ) = 0. 69 [Ri Ci + (Ri + Rj) Cj + (Ri + Rj + Rk)Ck] Spring 08, Feb 26 ELEC 7770: Advanced VLSI Design (Agrawal) 11

Finding δ(I, j) and Δ(I, j) Minimum delay Maximum delay , - A 1 , - 0, 0 B 3 3, 3 i , - Spring 08, Feb 26 C 1 D 2 H 9, 10 j 3 E 1 4, 4 G 2 , - F 1 5, 5 ELEC 7770: Advanced VLSI Design (Agrawal) 6, 7 J 6, 8 1 k 12

Maximum Clock Frequency for Tolerance ±q/2 in Skew Linear program: Minimize Tck Subject to: For all flip-flop pairs (i, j), xi + δ(i, j) ≥ xj + Thj + q xi + Δ(i, j) ≤ xj + Tck – Tsj – q Where q is a constant xi are variables, ximin ≤ xi Tck is a variable Spring 08, Feb 26 ELEC 7770: Advanced VLSI Design (Agrawal) 13

Maximum Tolerance for Given Clock Frequency Linear program: Maximize q Subject to: For all flip-flop pairs (i, j), xi + δ(i, j) ≥ xj + Thj + q xi + Δ(i, j) ≤ xj + Tck – Tsj – q Where Tck is a constant xi are variables, ximin ≤ xi q is a variable Spring 08, Feb 26 ELEC 7770: Advanced VLSI Design (Agrawal) 14

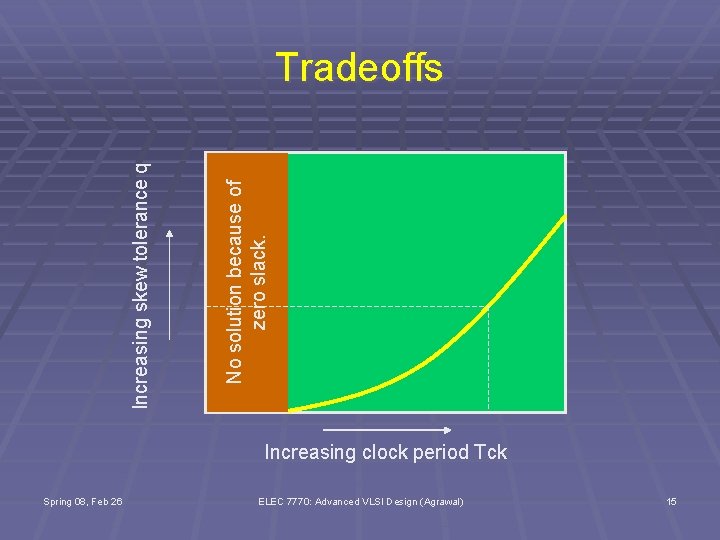
No solution because of zero slack. Increasing skew tolerance q Tradeoffs Increasing clock period Tck Spring 08, Feb 26 ELEC 7770: Advanced VLSI Design (Agrawal) 15

Clock Skew Problem § N. Maheshwari and S. S. Sapatnekar, Timing § Analysis and Optimization of Sequential Circuits, Springer, 1999. J. P. Fishburn, “Clock Skew Optimization, ” IEEE Trans. Computers, vol. 39, no. 7, pp. 945 -951, July 1990. Spring 08, Feb 26 ELEC 7770: Advanced VLSI Design (Agrawal) 16