ELEC 52706270 Spring 2009 LowPower Design of Electronic

ELEC 5270/6270 Spring 2009 Low-Power Design of Electronic Circuits Linear Programming – A Mathematical Optimization Technique Vishwani D. Agrawal James J. Danaher Professor Dept. of Electrical and Computer Engineering Auburn University, Auburn, AL 36849 vagrawal@eng. auburn. edu http: //www. eng. auburn. edu/~vagrawal/COURSE/E 6270_Spr 09/course. html Copyright Agrawal, 2009 ELEC 6270 Spring 09, Lecture 8 1

What is Linear Programming Linear programming (LP) is a mathematical method for selecting the best solution from the available solutions of a problem. l Method: l l State the problem and define variables whose values will be determined. l Develop a linear programming model: l l Write the problem as an optimization formula (a linear expression to be minimized or maximized) Write a set of linear constraints l An available LP solver (computer program) gives the values of variables. Copyright Agrawal, 2009 ELEC 6270 Spring 09, Lecture 8 2

Types of LPs LP – all variables are real. l ILP – all variables are integers. l MILP – some variables are integers, others are real. l A reference: l l S. I. Gass, An Illustrated Guide to Linear Programming, New York: Dover, 1990. Copyright Agrawal, 2009 ELEC 6270 Spring 09, Lecture 8 3

A Single-Variable Problem Consider variable x l Problem: find the maximum value of x subject to constraint, 0 ≤ x ≤ 15. l Solution: x = 15. l Constraint satisfied 0 15 x Solution x = 15 Copyright Agrawal, 2009 ELEC 6270 Spring 09, Lecture 8 4

Single Variable Problem (Cont. ) l l Consider more complex constraints: Maximize x, subject to following constraints: l l x≥ 0 5 x ≤ 75 6 x ≤ 30 x ≤ 10 0 (1) (2) (3) (4) 5 10 15 (2) (3) x (1) (4) All constraints satisfied Solution, x = 5 Copyright Agrawal, 2009 ELEC 6270 Spring 09, Lecture 8 5

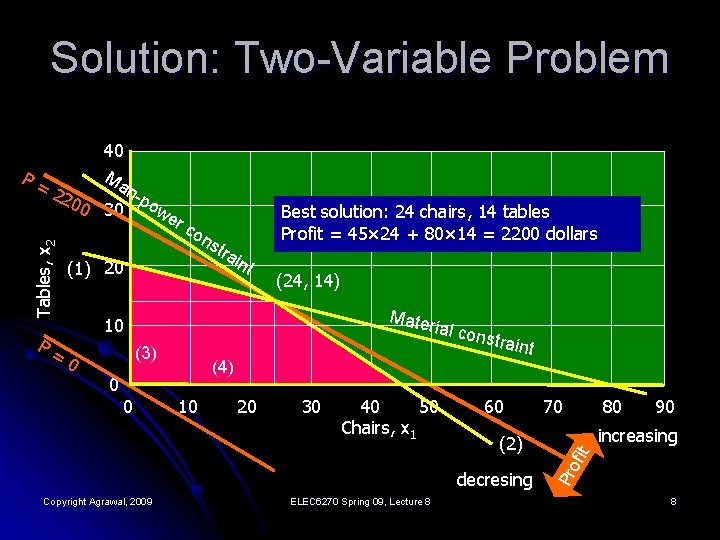
A Two-Variable Problem l Manufacture of chairs and tables: l Resources available: l Material: 400 boards of wood l Labor: 450 man-hours l Profit: l Chair: $45 l Table: $80 l Resources needed: l Chair l l l Table l l l 5 boards of wood 10 man-hours 20 boards of wood 15 man-hours Problem: How many chairs and how many tables should be manufactured to maximize the total profit? Copyright Agrawal, 2009 ELEC 6270 Spring 09, Lecture 8 6

Formulating Two-Variable Problem Manufacture x 1 chairs and x 2 tables to maximize profit: P = 45 x 1 + 80 x 2 dollars l Subject to given resource constraints: l l 400 boards of wood, 5 x 1 + 20 x 2 ≤ 400 l 450 man-hours of labor, 10 x 1 + 15 x 2 ≤ 450 l x 1 ≥ 0 l x 2 ≥ 0 Copyright Agrawal, 2009 ELEC 6270 Spring 09, Lecture 8 (1) (2) (3) (4) 7

Solution: Two-Variable Problem n 00 30 -pow er co ns P= (1) 20 tra i Best solution: 24 chairs, 14 tables Profit = 45× 24 + 80× 14 = 2200 dollars nt (24, 14) Mater ia 10 l cons (3) 0 (4) 0 0 10 20 30 40 50 Chairs, x 1 traint 60 (2) decresing Copyright Agrawal, 2009 ELEC 6270 Spring 09, Lecture 8 70 80 90 increasing Pro fit 22 Tables, x 2 P= 40 Ma 8

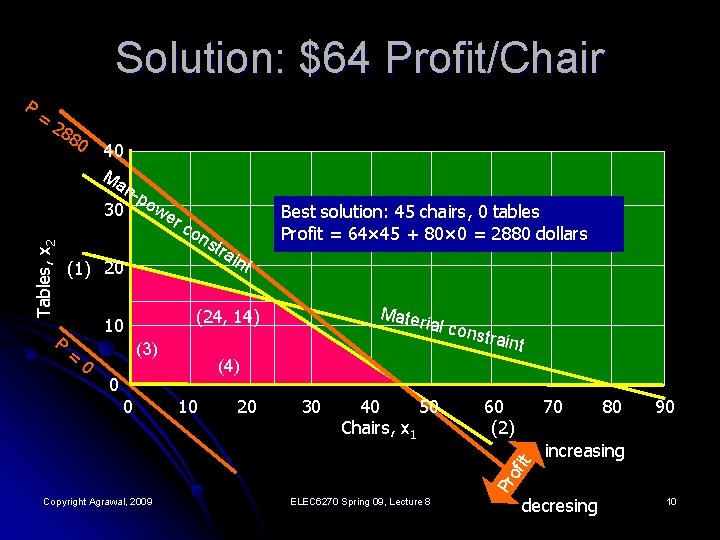
Change Profit of Chair to $64/Unit Manufacture x 1 chairs and x 2 tables to maximize profit: P = 64 x 1 + 80 x 2 dollars l Subject to given resource constraints: l l 400 boards of wood, 5 x 1 + 20 x 2 ≤ 400 l 450 man-hours of labor, 10 x 1 + 15 x 2 ≤ 450 l x 1 ≥ 0 l x 2 ≥ 0 Copyright Agrawal, 2009 ELEC 6270 Spring 09, Lecture 8 (1) (2) (3) (4) 9

Solution: $64 Profit/Chair = 28 80 40 Ma n-p 30 owe rc Tables, x 2 P on s (1) 20 (3) 0 nt Mater ia (24, 14) 10 = tra i Best solution: 45 chairs, 0 tables Profit = 64× 45 + 80× 0 = 2880 dollars traint (4) 0 10 20 30 40 50 Chairs, x 1 60 (2) 70 it 0 l cons 80 90 increasing Pr of P Copyright Agrawal, 2009 ELEC 6270 Spring 09, Lecture 8 decresing 10

A Dual Problem Explore an alternative. l Questions: l Should we make tables and chairs? l Or, auction off the available resources? l l To answer this question we need to know: What is the minimum price for the resources that will provide us with same amount of revenue from sale as the profits from tables and chairs? l This is the dual of the original problem. l Copyright Agrawal, 2009 ELEC 6270 Spring 09, Lecture 8 11

Formulating the Dual Problem l Revenue received by selling off resources: For each board, w 1 l For each man-hour, w 2 l Minimize 400 w 1 + 450 w 2 l Subject to constraints: l l 5 w 1 + 10 w 2 l 20 w 1 + 15 w 2 l w 1 ≥ 0 l w 2 ≥ 0 Copyright Agrawal, 2009 ≥ 45 ≥ 80 Resources: Material: 400 boards Labor: 450 man-hrs Profit: Chair: $45 Table: $80 Resources needed: Chair 5 boards of wood 10 man-hours Table 20 boards of wood 15 man-hours ELEC 6270 Spring 09, Lecture 8 12

The Duality Theorem l If the primal has a finite optimum solution, so does the dual, and the optimum values of the objective functions are equal. Copyright Agrawal, 2009 ELEC 6270 Spring 09, Lecture 8 13

Primal-Dual Problems l Primal problem l l l Fixed resources Maximize profit l l l l x 1 (number of chairs) x 2 (number of tables) Maximize profit 45 x 1+80 x 2 Subject to: l 5 x 1 + 20 x 2 10 x 1 + 15 x 2 x 1 x 2 l Variables: l l l l w 1 ($ value/board of wood) w 2 ($ value/man-hour) Minimize value 400 w 1+450 w 2 Subject to: l x 1 = 24 chairs, x 2 = 14 tables Profit = $2200 Copyright Agrawal, 2009 Fixed profit Minimize value l ≤ 400 ≤ 450 ≥ 0 Solution: l Dual Problem l Variables: l l l 5 w 1 + 10 w 2 20 w 1 + 15 w 2 w 1 w 2 ≥ 45 ≥ 80 ≥ 0 Solution: l l ELEC 6270 Spring 09, Lecture 8 w 1 = $1, w 2 = $4 value = $2200 14

LP for n Variables n minimize Σ cj xj Objective function j =1 n subject to Σ aij xj ≤ bi, i = 1, 2, . . . , m j =1 n Σ cij xj = di, i = 1, 2, . . . , p j =1 Variables: xj Constants: cj, aij, bi, cij, di Copyright Agrawal, 2009 ELEC 6270 Spring 09, Lecture 8 15

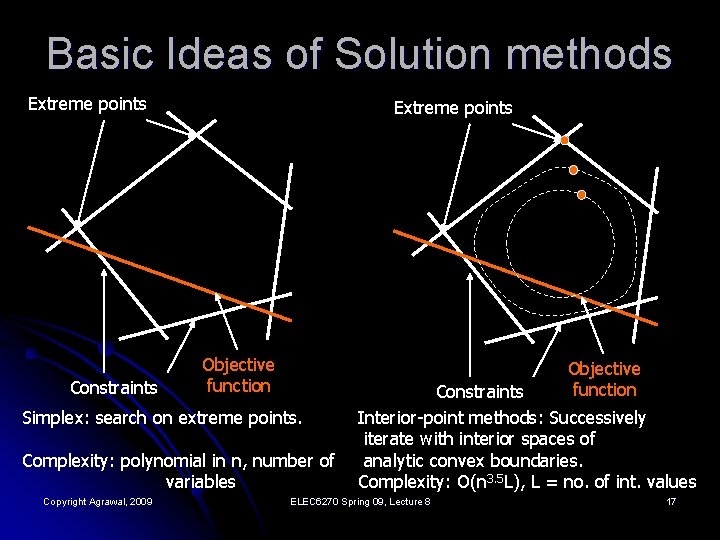
Algorithms for Solving LP l Simplex method l l Ellipsoid method l l L. G. Khachiyan, “A Polynomial Algorithm for Linear Programming, ” Soviet Math. Dokl. , vol. 20, pp. 191 -194, 1984. Interior-point method l l G. B. Dantzig, Linear Programming and Extension, Princeton, New Jersey, Princeton University Press, 1963. N. K. Karmarkar, “A New Polynomial-Time Algorithm for Linear Programming, ” Combinatorica, vol. 4, pp. 373 -395, 1984. Course website of Prof. Lieven Vandenberghe (UCLA), http: //www. ee. ucla. edu/ee 236 a. html Copyright Agrawal, 2009 ELEC 6270 Spring 09, Lecture 8 16

Basic Ideas of Solution methods Extreme points Constraints Extreme points Objective function Simplex: search on extreme points. Complexity: polynomial in n, number of variables Copyright Agrawal, 2009 Constraints Interior-point methods: Successively iterate with interior spaces of analytic convex boundaries. Complexity: O(n 3. 5 L), L = no. of int. values ELEC 6270 Spring 09, Lecture 8 17

Integer Linear Programming (ILP) Variables are integers. l Complexity is exponential – higher than LP. l LP relaxation l l Convert all variables to real, preserve ranges. l LP solution provides guidance. l Rounding LP solution can provide a nonoptimal solution. Copyright Agrawal, 2009 ELEC 6270 Spring 09, Lecture 8 18

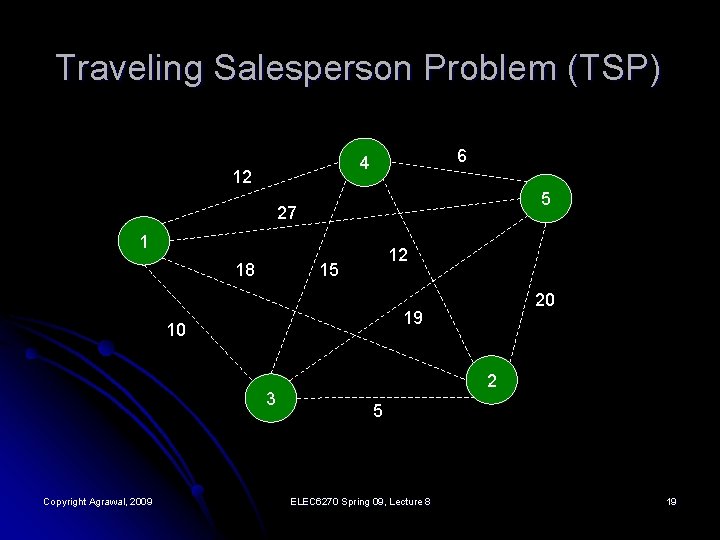
Traveling Salesperson Problem (TSP) 6 4 12 5 27 1 18 12 15 19 10 3 Copyright Agrawal, 2009 20 2 5 ELEC 6270 Spring 09, Lecture 8 19

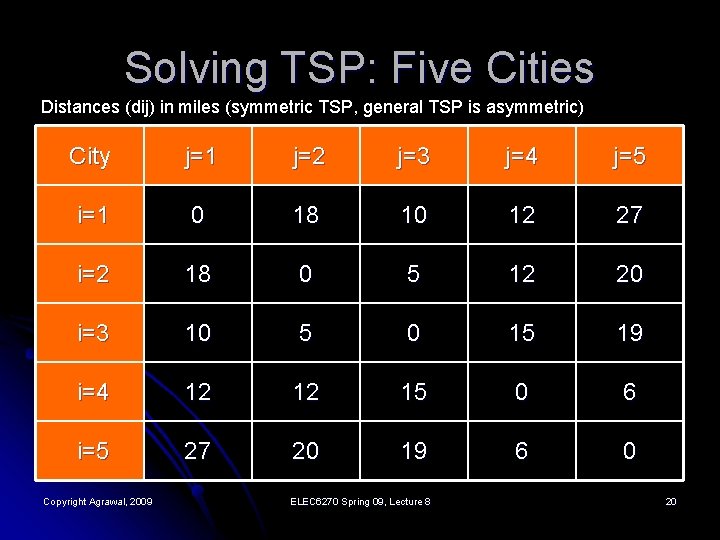
Solving TSP: Five Cities Distances (dij) in miles (symmetric TSP, general TSP is asymmetric) City j=1 j=2 j=3 j=4 j=5 i=1 0 18 10 12 27 i=2 18 0 5 12 20 i=3 10 5 0 15 19 i=4 12 12 15 0 6 i=5 27 20 19 6 0 Copyright Agrawal, 2009 ELEC 6270 Spring 09, Lecture 8 20

Search Space: No. of Tours l Asymmetric TSP tours l Five-city problem: 4 × 3 × 2 × 1 = 24 tours l Ten-city problem: 362, 880 tours l 15 -city problem: 87, 178, 291, 200 tours l 50 -city problem: 49! = 6. 08× 1062 tours Time for enumerative search assuming 1 μs per tour evaluation = 1. 93× 1055 years Copyright Agrawal, 2009 ELEC 6270 Spring 09, Lecture 8 21

A Greedy Heuristic Solution Tour length = 10 + 5 + 12 + 6 + 27 = 60 miles (non-optimal) City j=1 j=2 j=3 j=4 j=5 i=1 (start) 0 18 10 12 27 i=2 18 0 5 12 20 i=3 10 5 0 15 19 i=4 12 12 15 0 6 i=5 27 20 19 6 0 Copyright Agrawal, 2009 ELEC 6270 Spring 09, Lecture 8 22

ILP Variables, Constants and Constraints x 14 ε [0, 1] d 14 = 12 4 5 x 15 ε [0, 1] d 15 = 27 x 12 ε [0, 1] d 12 = 18 1 x 13 ε [0, 1] d 13 = 10 Integer variables: xij = 1, travel i to j xij = 0, do not travel i to j 2 3 Real constants: dij = distance from i to j x 12 + x 13 + x 14 + x 15 = 1 four other similar equations Copyright Agrawal, 2009 ELEC 6270 Spring 09, Lecture 8 23

Objective Function and ILP Solution 5 i-1 Minimize ∑ ∑ xij × dij i=1 j=1 ∑ xij = 1 j≠i Copyright Agrawal, 2009 for all i xij j=1 2 3 4 5 i=1 0 0 2 1 0 0 3 0 1 0 0 0 4 0 0 1 5 0 0 0 1 0 ELEC 6270 Spring 09, Lecture 8 24

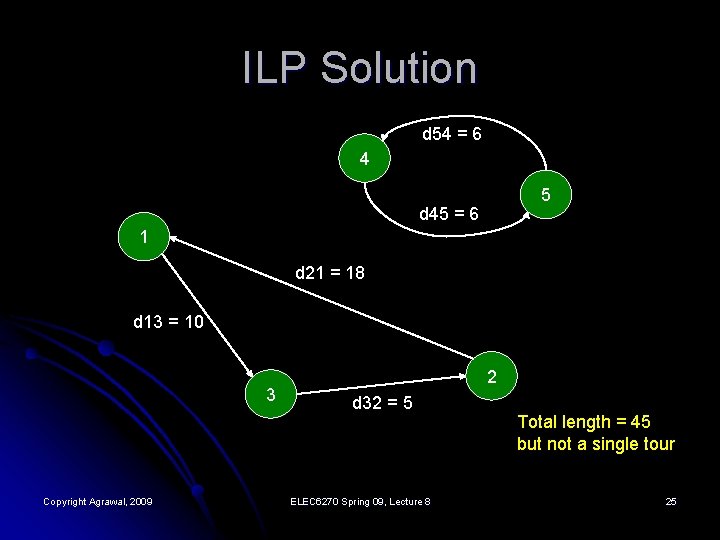
ILP Solution d 54 = 6 4 5 d 45 = 6 1 d 21 = 18 d 13 = 10 3 Copyright Agrawal, 2009 2 d 32 = 5 ELEC 6270 Spring 09, Lecture 8 Total length = 45 but not a single tour 25

Additional Constraints for Single Tour l Following constraints prevent split tours. For any subset S of cities, the tour must enter and exit that subset: ∑ xij ≥ 2 for all S, |S| < 5 i ε S j ε S Remaining set At least two arrows must cross this boundary. Any subset Copyright Agrawal, 2009 ELEC 6270 Spring 09, Lecture 8 26

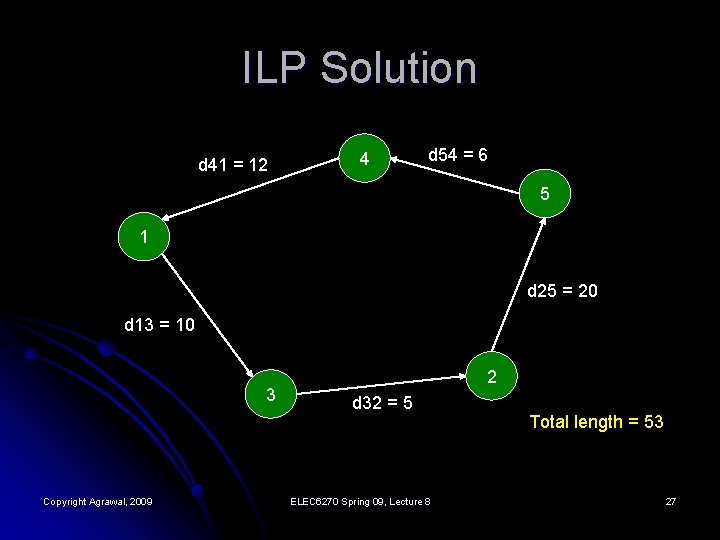
ILP Solution d 41 = 12 4 d 54 = 6 5 1 d 25 = 20 d 13 = 10 3 Copyright Agrawal, 2009 2 d 32 = 5 ELEC 6270 Spring 09, Lecture 8 Total length = 53 27

Characteristics of ILP l l l Worst-case complexity is exponential in number of variables. Linear programming (LP) relaxation, where integer variables are treated as real, gives a lower bound on the objective function. Recursive rounding of relaxed LP solution to nearest integers gives an approximate solution to the ILP problem. l K. R. Kantipudi and V. D. Agrawal, “A Reduced Complexity Algorithm for Minimizing N-Detect Tests, ” Proc. 20 th International Conf. VLSI Design, January 2007, pp. 492 -497. Copyright Agrawal, 2009 ELEC 6270 Spring 09, Lecture 8 28

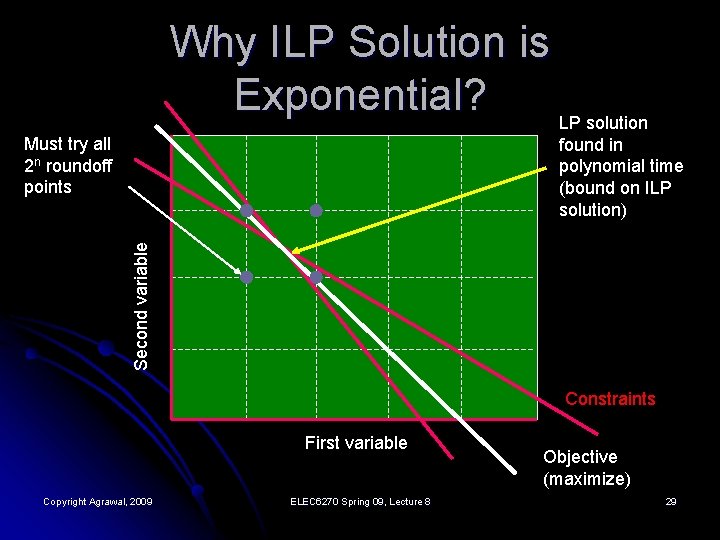
Why ILP Solution is Exponential? LP solution Must try all 2 n roundoff points Second variable found in polynomial time (bound on ILP solution) Constraints First variable Copyright Agrawal, 2009 ELEC 6270 Spring 09, Lecture 8 Objective (maximize) 29

ILP Example: Test Minimization l l A combinational circuit has n test vectors that detect m faults. Each test detects a subset of faults. Find the smallest subset of test vectors that detects all m faults. ILP model: l l Assign an integer variable ti ε [0, 1] to ith test vector such that ti = 1, if we select ti, otherwise ti= 0. Define an integer constant fij ε [0, 1] such that fij = 1, if ith vector detects jth fault, otherwise fij = 0. Values of constants fij are determined by fault simulation. Copyright Agrawal, 2009 ELEC 6270 Spring 09, Lecture 8 30

Test Minimization by ILP n Σ ti minimize Objective function i=1 n subject to Σ fij ti ≥ 1, j = 1, 2, . . . , m i=1 Copyright Agrawal, 2009 ELEC 6270 Spring 09, Lecture 8 31

3 V 3 F: A 3 -Vector 3 -Fault Example Test vector i fij i=1 i=2 i=3 Variables: t 1, t 2, t 3 ε [0, 1] Minimize t 1 + t 2 + t 3 Fault j j=1 1 1 0 Subject to: t 1 + t 2 ≥ 1 j=2 0 1 1 j=3 1 0 1 Copyright Agrawal, 2009 ELEC 6270 Spring 09, Lecture 8 t 2 + t 3 ≥ 1 t 1 + t 3 ≥ 1 32

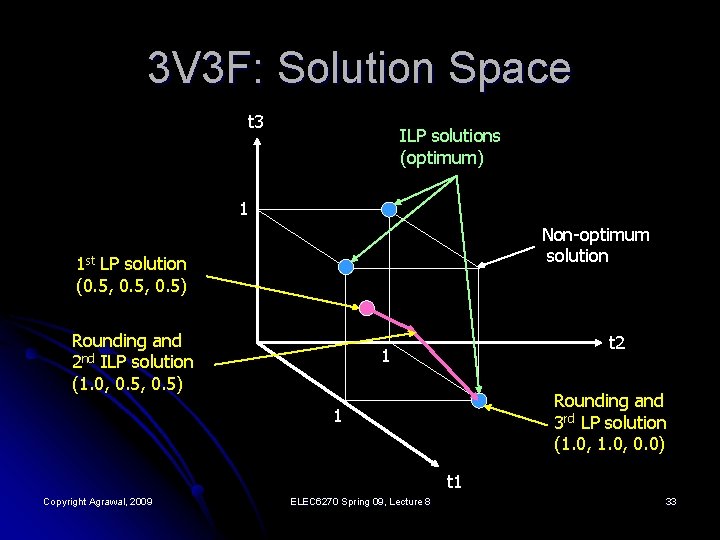
3 V 3 F: Solution Space t 3 ILP solutions (optimum) 1 Non-optimum solution 1 st LP solution (0. 5, 0. 5) Rounding and 2 nd ILP solution (1. 0, 0. 5) t 2 1 Rounding and 3 rd LP solution (1. 0, 0. 0) 1 t 1 Copyright Agrawal, 2009 ELEC 6270 Spring 09, Lecture 8 33

3 V 3 F: LP Relaxation and Rounding ILP – Variables: t 1, t 2, t 3 ε [0, 1] LP relaxation: t 1, t 2, t 3 ε (0. 0, 1. 0) Minimize t 1 + t 2 + t 3 Solution: t 1 = t 2 = t 3 = 0. 5 Subject to: Recursive rounding: t 1 + t 2 ≥ 1 t 2 + t 3 ≥ 1 t 1 + t 3 ≥ 1 (1) round one variable, t 1 = 1. 0 Two-variable LP problem: Minimize t 2 + t 3 subject to t 2 + t 3 ≥ 1. 0 LP solution t 2 = t 3 = 0. 5 (2) round a variable, t 2 = 1. 0 ILP constraints are satisfied solution is t 1 = 1, t 2 = 1, t 3 = 0 Copyright Agrawal, 2009 ELEC 6270 Spring 09, Lecture 8 34

Recursive Rounding Algorithm 1. 2. 3. 4. Obtain a relaxed LP solution. Stop if each variable in the solution is an integer. Round the variable closest to an integer. Remove any constraints that are now unconditionally satisfied. Go to step 1. Copyright Agrawal, 2009 ELEC 6270 Spring 09, Lecture 8 35

Recursive Rounding l l ILP has exponential complexity. Recursive rounding: l l ILP is transformed into k LPs with progressively reducing number of variables. A solution that satisfies all constraints is guaranteed; this solution is often close to optimal. Number of LPs, k, is the size of the final solution, i. e. , the number of non-zero variables in the test minimization problem. Recursive rounding complexity is k × O(np), where k ≤ n, n is number of variables. Copyright Agrawal, 2009 ELEC 6270 Spring 09, Lecture 8 36

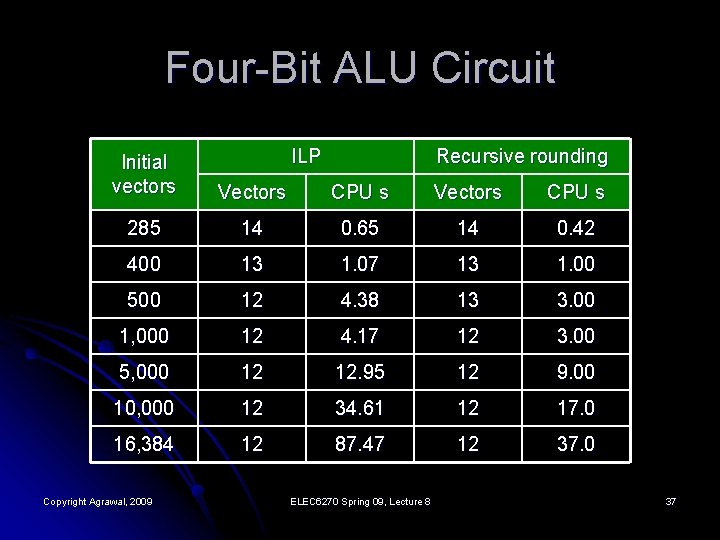
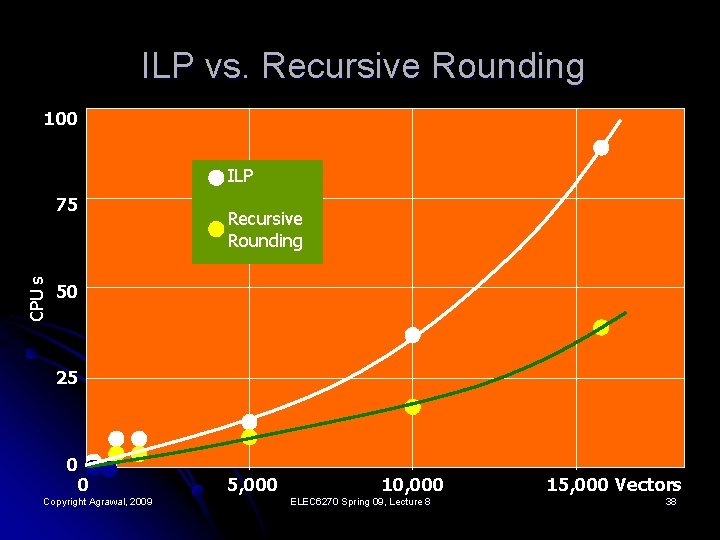
Four-Bit ALU Circuit ILP Recursive rounding Initial vectors Vectors CPU s 285 14 0. 65 14 0. 42 400 13 1. 07 13 1. 00 500 12 4. 38 13 3. 00 1, 000 12 4. 17 12 3. 00 5, 000 12 12. 95 12 9. 00 10, 000 12 34. 61 12 17. 0 16, 384 12 87. 47 12 37. 0 Copyright Agrawal, 2009 ELEC 6270 Spring 09, Lecture 8 37

ILP vs. Recursive Rounding 100 ILP CPU s 75 Recursive Rounding 50 25 0 0 Copyright Agrawal, 2009 5, 000 10, 000 ELEC 6270 Spring 09, Lecture 8 15, 000 Vectors 38

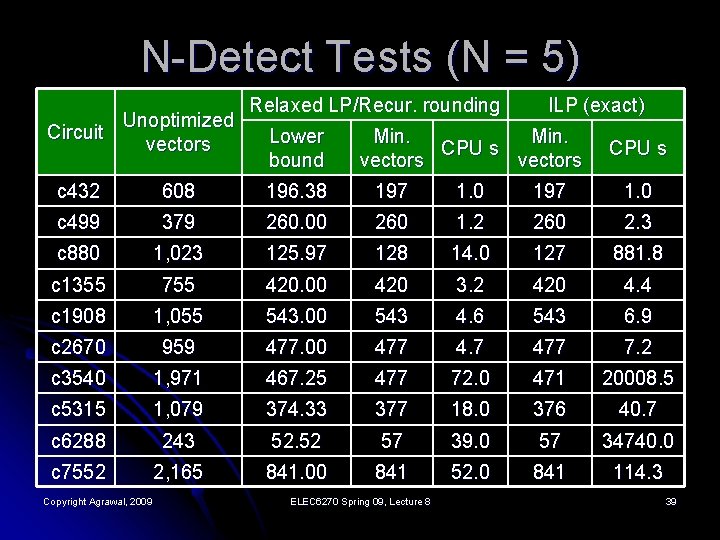
N-Detect Tests (N = 5) Relaxed LP/Recur. rounding ILP (exact) Circuit Unoptimized vectors c 432 608 196. 38 197 1. 0 c 499 379 260. 00 260 1. 2 260 2. 3 c 880 1, 023 125. 97 128 14. 0 127 881. 8 c 1355 755 420. 00 420 3. 2 420 4. 4 c 1908 1, 055 543. 00 543 4. 6 543 6. 9 c 2670 959 477. 00 477 4. 7 477 7. 2 c 3540 1, 971 467. 25 477 72. 0 471 20008. 5 c 5315 1, 079 374. 33 377 18. 0 376 40. 7 c 6288 243 52. 52 57 39. 0 57 34740. 0 c 7552 2, 165 841. 00 841 52. 0 841 114. 3 Copyright Agrawal, 2009 Lower bound Min. CPU s vectors ELEC 6270 Spring 09, Lecture 8 CPU s 39

Finding LP/ILP Solvers l l l R. Fourer, D. M. Gay and B. W. Kernighan, AMPL: A Modeling Language for Mathematical Programming, South San Francisco, California: Scientific Press, 1993. Several of programs described in this book are available to Auburn users. B. R. Hunt, R. L. Lipsman, J. M. Rosenberg, K. R. Coombes, J. E. Osborn and G. J. Stuck, A Guide to MATLAB for Beginners and Experienced Users, Cambridge University Press, 2006. Search the web. Many programs with small number of variables can be downloaded free. Copyright Agrawal, 2009 ELEC 6270 Spring 09, Lecture 8 40

A Circuit Optimization Problem l Given: l Circuit netlist l Cell library with multiple versions for each cell l Select cell versions to optimize a specified characteristic of the circuit. Typical characteristics are: l Area l Power l Delay Copyright Agrawal, 2009 ELEC 6270 Spring 09, Lecture 8 41

Example: NAND(X), X = 0 or 1 l X=0 l Delay = nominal delay (d) l Power = 3 × nominal power (p) l X=1 l Delay = 2 × nominal delay (d) l Power = 0. 5 × nominal power (p) Gate delay = (1 – X) d + 2 X d l Power = 3(1 – X) p + 0. 5 X p l Copyright Agrawal, 2009 ELEC 6270 Spring 09, Lecture 8 42

Constraint: Gate k in the Circuit Ti = signal arrival time at ith input l Tk = signal arrival time at gate output l Tk ≥ Ti + (1 – Xk) dk + 2 Xk dk, for all i l Where, dk = nominal delay of gate Xk = 0 or 1, specifies version of cell l Copyright Agrawal, 2009 ELEC 6270 Spring 09, Lecture 8 43

Clock Constraints Tk = 0, for all primary inputs l Tk ≤ clock period, for all primary outputs Combinational Logic Register l Clock Copyright Agrawal, 2009 ELEC 6270 Spring 09, Lecture 8 44

Optimization Function l Minimize ∑ 3(1 – Xk) pk + 0. 5 Xk pk all k where pk = nominal power consumption of gate k Copyright Agrawal, 2009 ELEC 6270 Spring 09, Lecture 8 45