Elasticity and Equation of State Lars Stixrude University

Elasticity and Equation of State Lars Stixrude University of Michigan

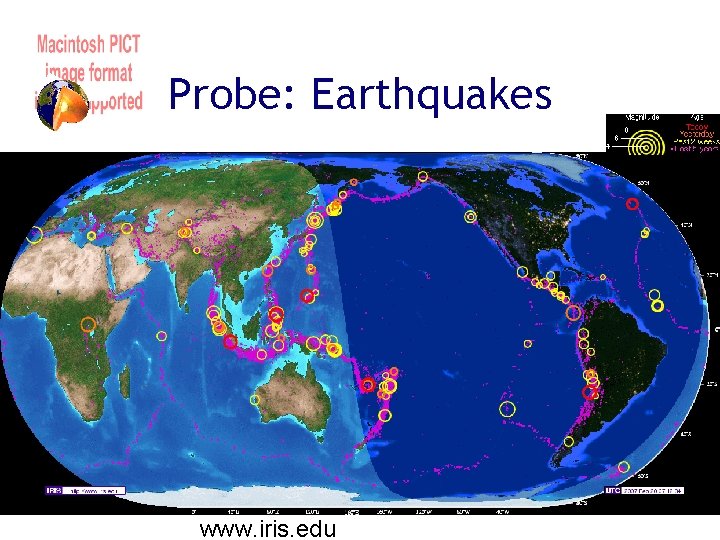
Probe: Earthquakes www. iris. edu

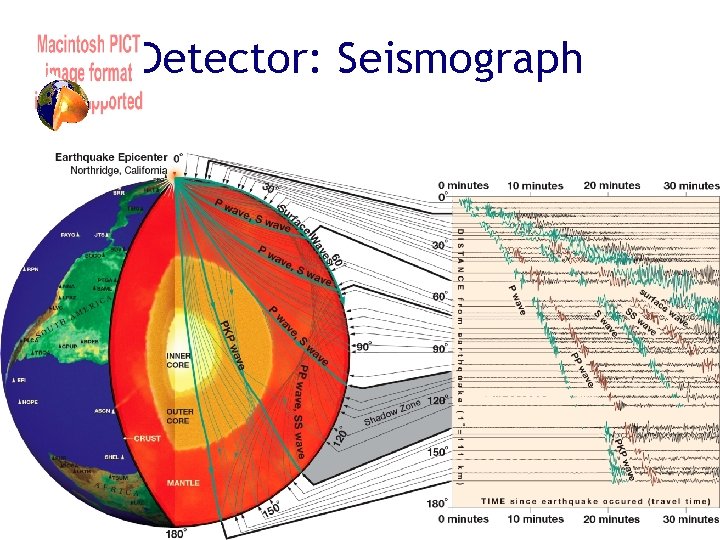
Detector: Seismograph

Determine: Elastic Wave Velocities To a good approximation: Radially homnogeneous Isotropic Small but important: Lateral heterogeneity Anisotropy

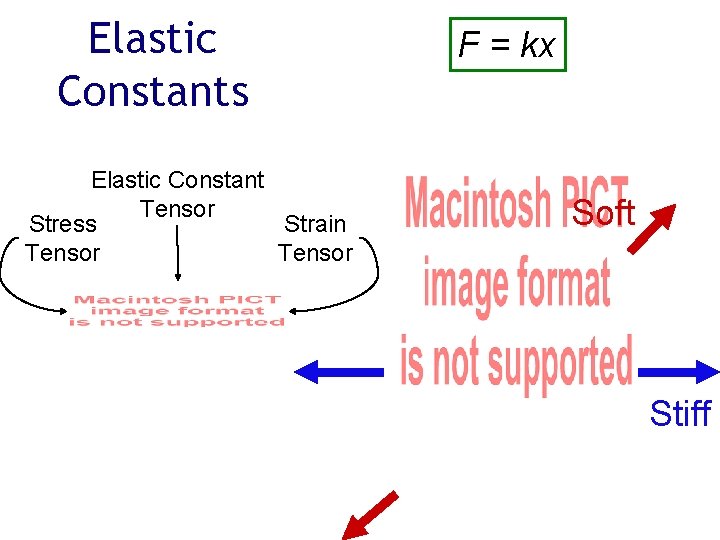
Elastic Constants Elastic Constant Tensor Stress Strain Tensor F = kx Soft Stiff

x, 1 Uniaxial stress (P wave) 11=c 1111 11 Elasticity 11=c 1122 22 y, 2 11 Poisson’s Ratio =- 22/ 11 = c 1122/c 1111 Fluid: =0. 5 i. e. volume conservation 22= 33=- 11/2 22 Crystals don’t conserve volume on uniaxial strain ~ 0. 25 Crystals stiffer, faster Pwave velocity

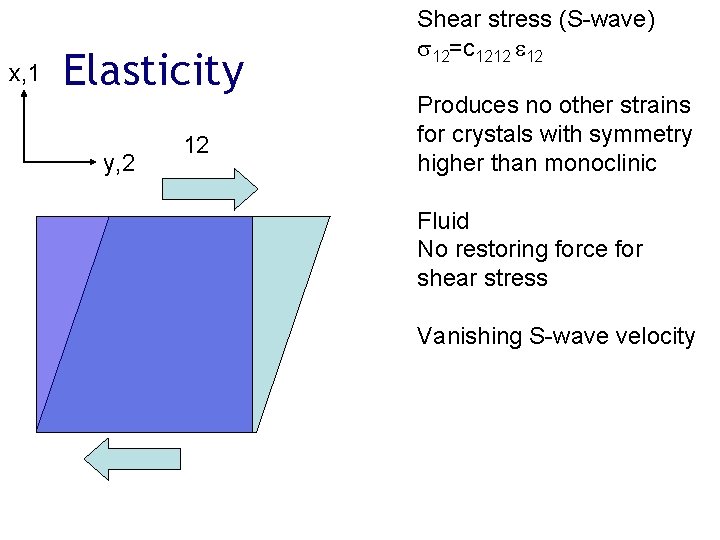
x, 1 Elasticity y, 2 12 Shear stress (S-wave) 12=c 1212 12 Produces no other strains for crystals with symmetry higher than monoclinic Fluid No restoring force for shear stress Vanishing S-wave velocity

cijkl Symmetry of elastic constant tensor Unchanged with respect to interchange of: i, j; k, l; ij, kl Crystalline symmetry: maximum 21 independent elastic constants Cubic: 1, 2, 3 directions equivalent Three independent elastic constants c 1111 (=c 2222=c 3333), c 1122, c 1212 Isotropic material: two independent elastic constants Bulk modulus: K=(c 1111+2 c 1122)/3 Shear modulus: G=(c 1111 -c 1122)/2=c 1212

Upper Mantle Xenolith, Depth ~ 100 km Red=garnet (gt); black=orthopyroxene (opx); green=clinopyroxene (cpx); yellowgreen=olivine (ol)

Isotropic Aggregates • Observation: Earth is nearly isotropic • But crystals are not! • They must be nearly randomly oriented • How to relate crystal cijkl to isotropic K, G? • How to “average” over elastic properties of coexisting crystals? • Constant stress (Voigt) • Constant strain (Reuss)

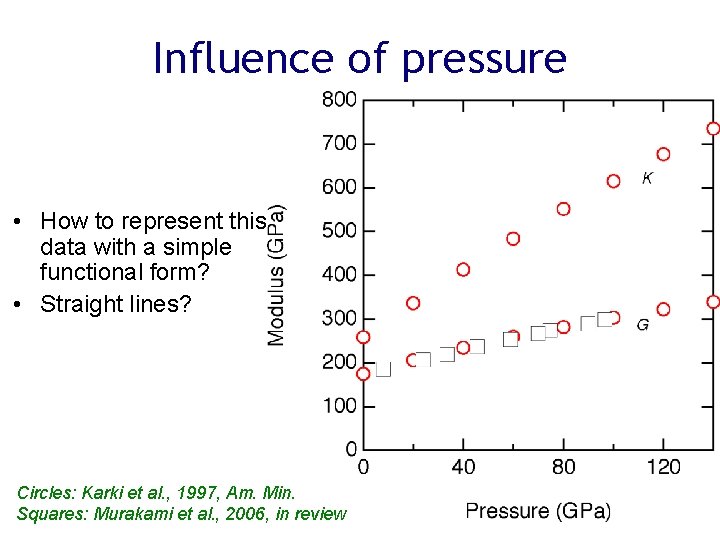
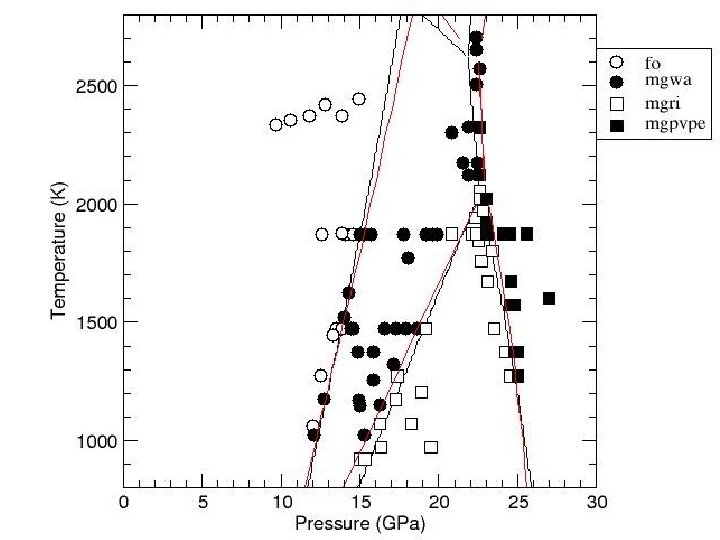
Influence of pressure • How to represent this data with a simple functional form? • Straight lines? Circles: Karki et al. , 1997, Am. Min. Squares: Murakami et al. , 2006, in review

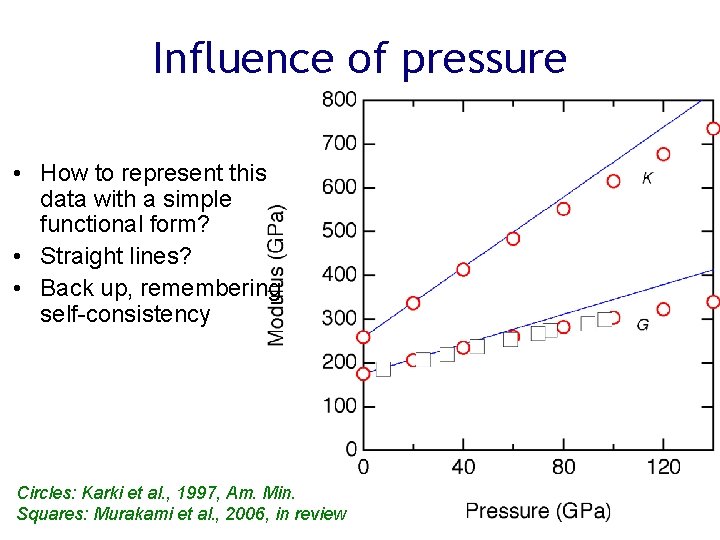
Influence of pressure • How to represent this data with a simple functional form? • Straight lines? • Back up, remembering self-consistency Circles: Karki et al. , 1997, Am. Min. Squares: Murakami et al. , 2006, in review

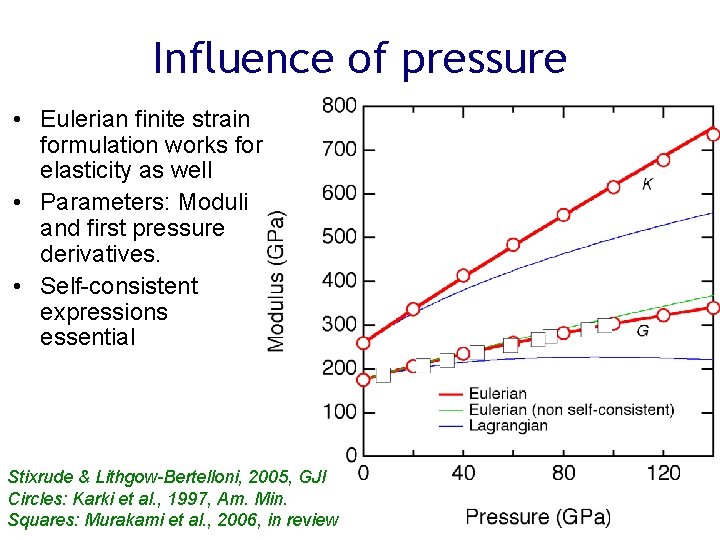
Influence of pressure • Eulerian finite strain formulation works for elasticity as well • Parameters: Moduli and first pressure derivatives. • Self-consistent expressions essential Stixrude & Lithgow-Bertelloni, 2005, GJI Circles: Karki et al. , 1997, Am. Min. Squares: Murakami et al. , 2006, in review

Influence of temperature • Most important effect: • Change in volume (density) • Moduli co-vary with density at similar rates whether density is altered by pressure or temperature • Microscopic picture: Lower density means weaker bonds and smaller moduli

Influence of composition • Iron has by far the largest influence • Most massive major element • Large influence on density • Increasing Fe content decreases velocities • Fe also lowers shear modulus

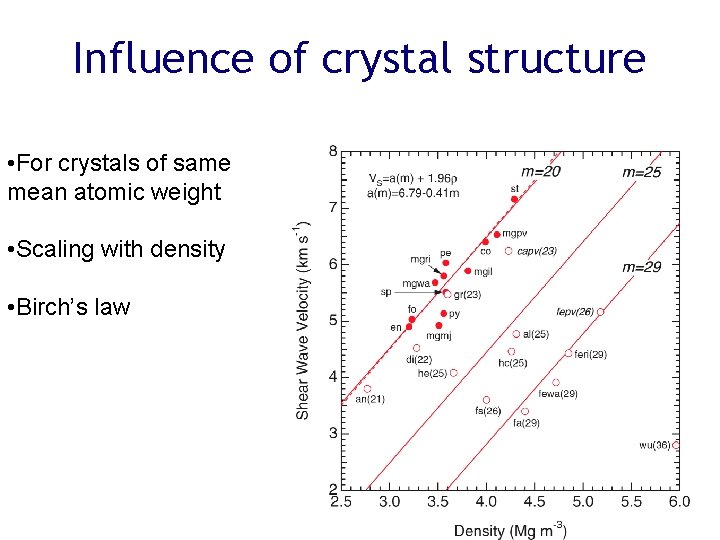
Influence of crystal structure • For crystals of same mean atomic weight • Scaling with density • Birch’s law

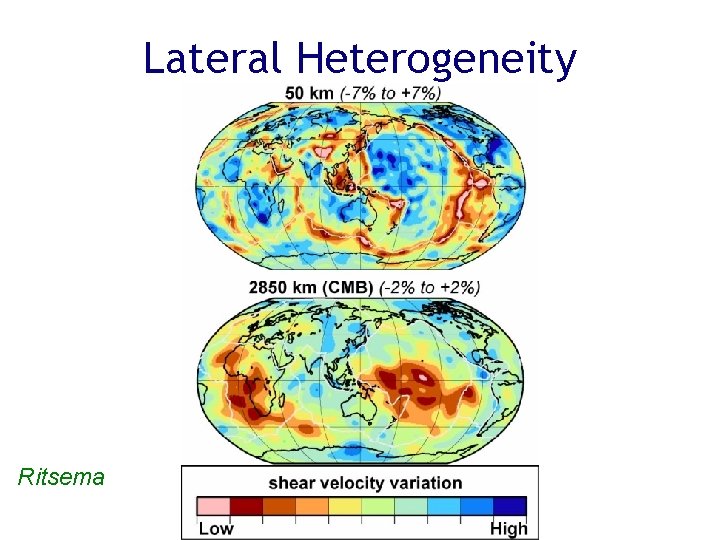
Lateral Heterogeneity Ritsema

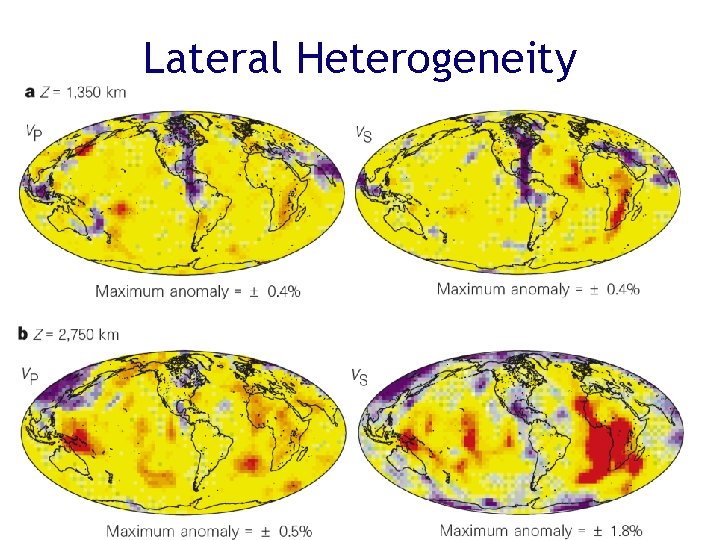
Lateral Heterogeneity

Influence of Temperature • VS and VP should co-vary with temperature! (both depend on G) • But they don’t near core-mantle boundary • Lateral heterogeneity must have other origin • Composition (iron content, reaction with core? ) • Phase (partial melt? )

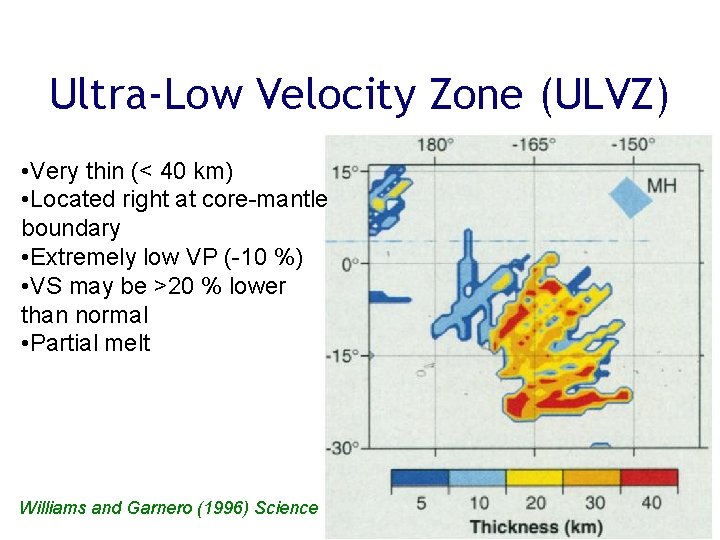
Ultra-Low Velocity Zone (ULVZ) • Very thin (< 40 km) • Located right at core-mantle boundary • Extremely low VP (-10 %) • VS may be >20 % lower than normal • Partial melt Williams and Garnero (1996) Science

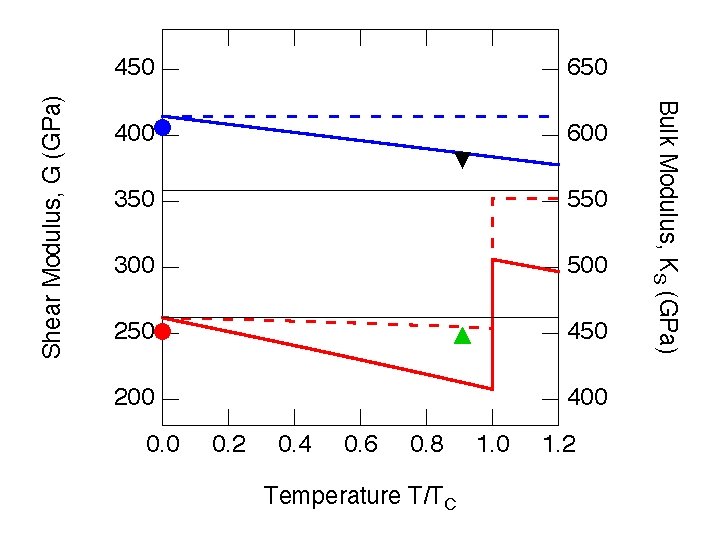
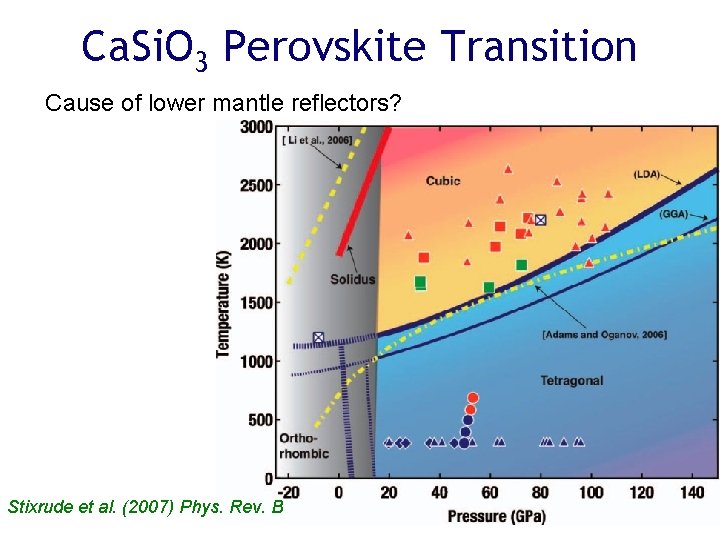
Ca. Si. O 3 Perovskite Transition Cause of lower mantle reflectors? Stixrude et al. (2007) Phys. Rev. B

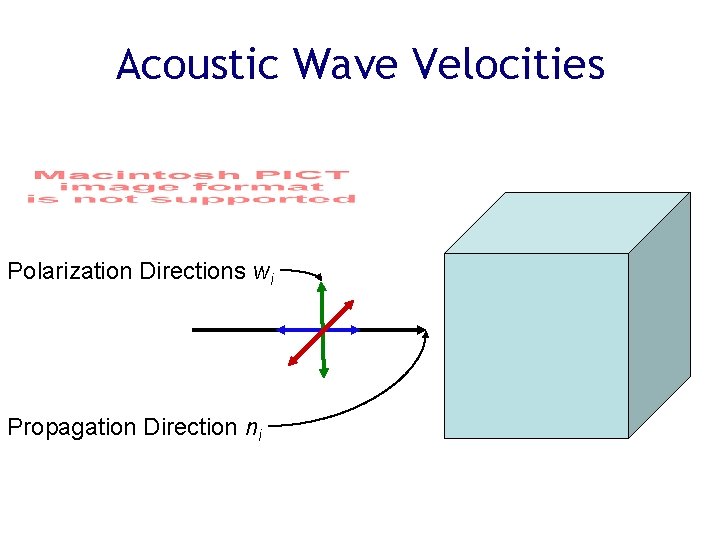
Acoustic Wave Velocities Polarization Directions wi Propagation Direction ni

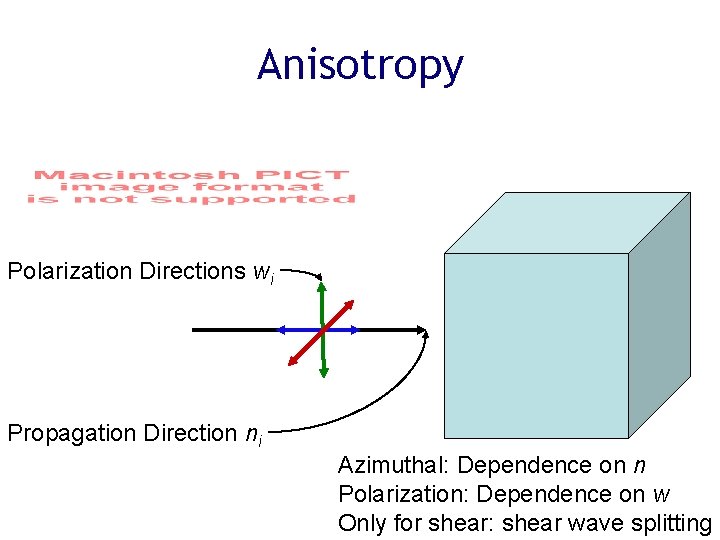
Anisotropy Polarization Directions wi Propagation Direction ni Azimuthal: Dependence on n Polarization: Dependence on w Only for shear: shear wave splitting

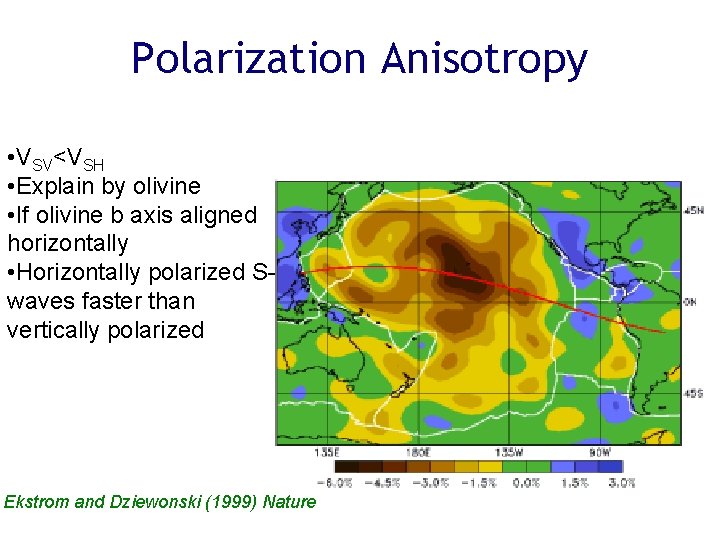
Polarization Anisotropy • VSV<VSH • Explain by olivine • If olivine b axis aligned horizontally • Horizontally polarized Swaves faster than vertically polarized Ekstrom and Dziewonski (1999) Nature

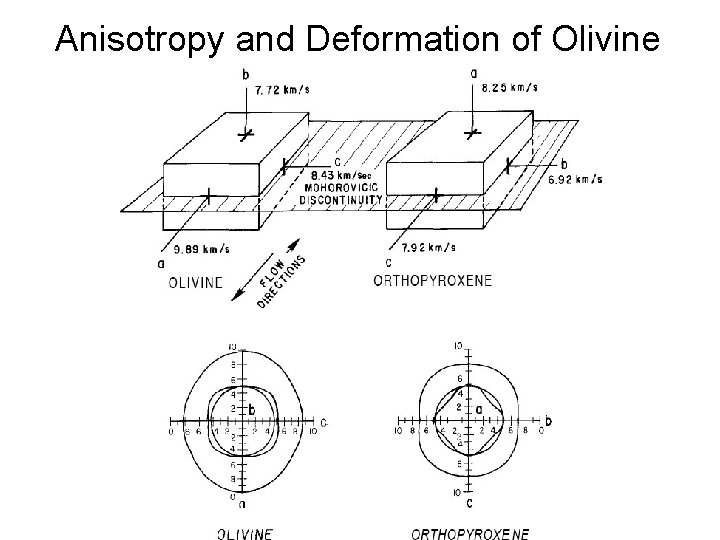
Anisotropy and Deformation of Olivine

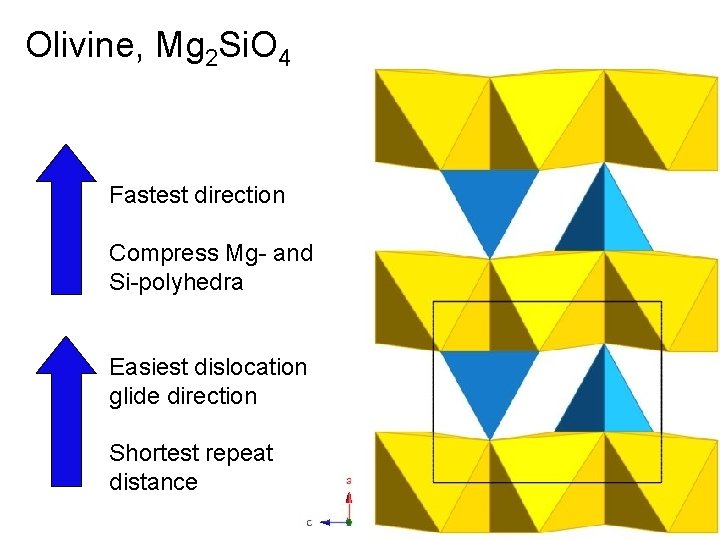
Olivine, Mg 2 Si. O 4 Fastest direction Compress Mg- and Si-polyhedra Easiest dislocation glide direction Shortest repeat distance

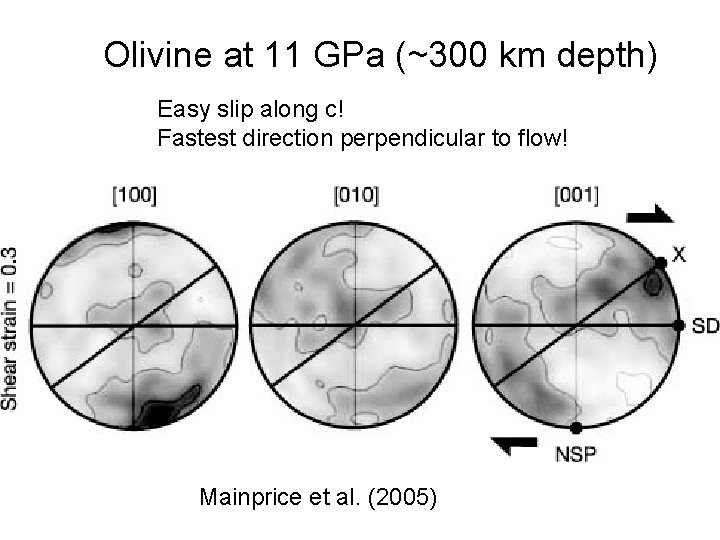
Olivine at 11 GPa (~300 km depth) Easy slip along c! Fastest direction perpendicular to flow! Mainprice et al. (2005)

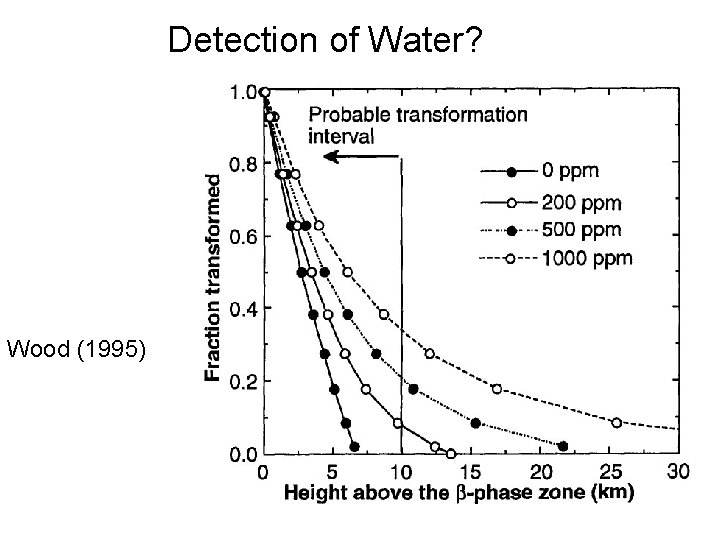
Detection of Water? Wood (1995)

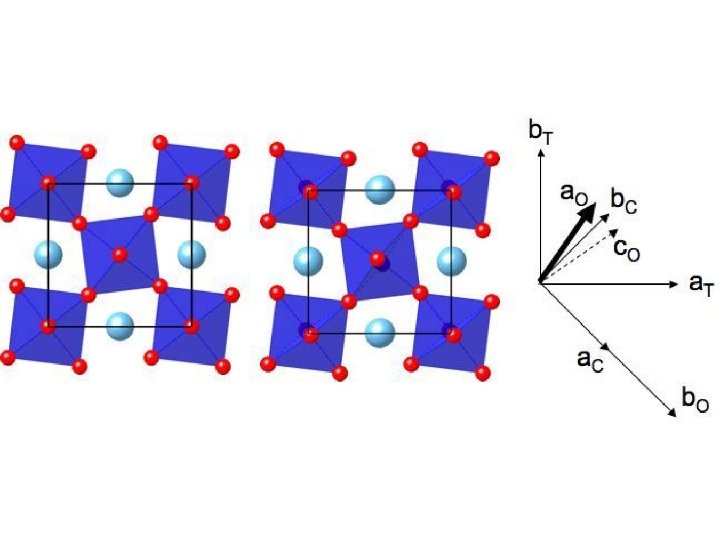
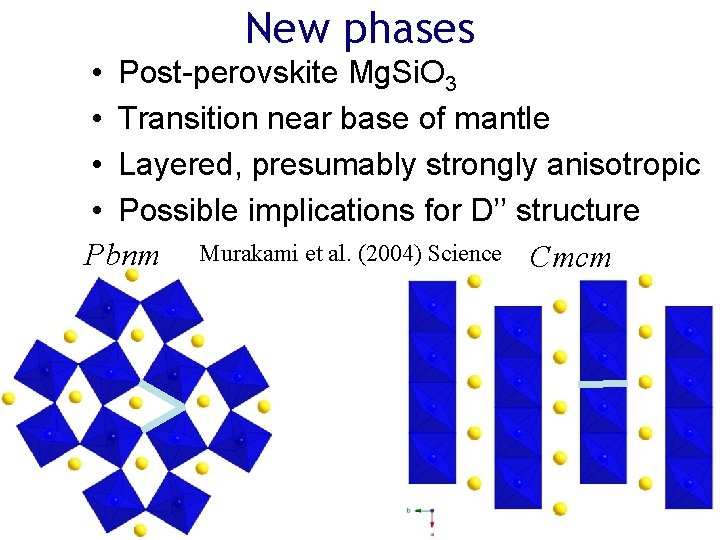
New phases • Post-perovskite Mg. Si. O 3 • Transition near base of mantle • Layered, presumably strongly anisotropic • Possible implications for D’’ structure Pbnm Murakami et al. (2004) Science Cmcm