Elastic properties Youngs moduli Poissons ratios Shear moduli

Elastic properties Young’s moduli Poisson’s ratios Shear moduli Bulk modulus John Summerscales

Elastic properties • Young’s moduli • uniaxial stress/unixaial strain • Poisson’s ratio • - transverse strain/strain parallel to the load • Shear moduli • biaxial stress/biaxial strain • Bulk modulus • triaxial stress (pressure)/triaxial strain

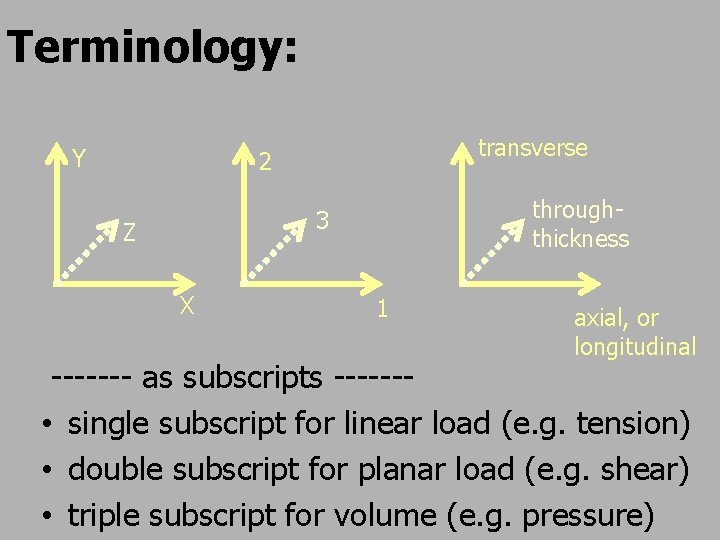
Terminology: Y transverse 2 throughthickness 3 Z X 1 axial, or longitudinal ------- as subscripts ------ • single subscript for linear load (e. g. tension) • double subscript for planar load (e. g. shear) • triple subscript for volume (e. g. pressure)

Stress component notation • first letter in the suffix for plane second letter for direction of stress • normal stress is positive if outward i. e. producing tension • shear stress is positive if it has same sense as corresponding normal stress. • Hooke’s law: σii = Ei ii

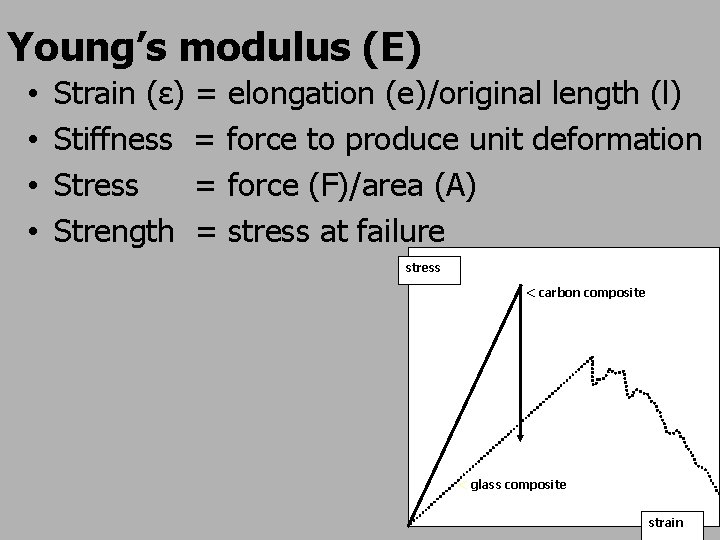
Young’s modulus (E) • • Strain (ε) = elongation (e)/original length (l) Stiffness = force to produce unit deformation Stress = force (F)/area (A) Strength = stress at failure stress < carbon composite < glass composite strain

Young’s moduli (Ei) E = Fl/e. A … but E in composites may vary with direction 3 principal axes (x, y, z)

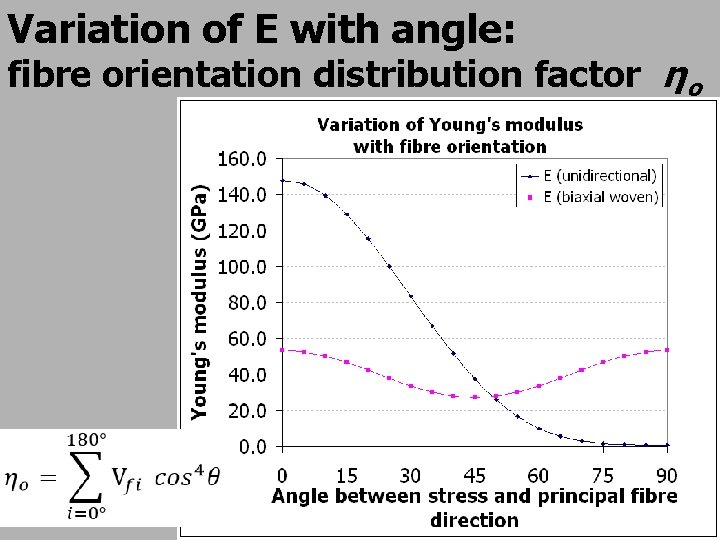
Variation of E with angle: fibre orientation distribution factor ηo

Load sharing models • Reuss model: • up to 0. 5% strain, equal stress in both the fibres and the matrix. • Voigt model • above 0. 5% strain, equal increases in strain in both fibre and matrix.

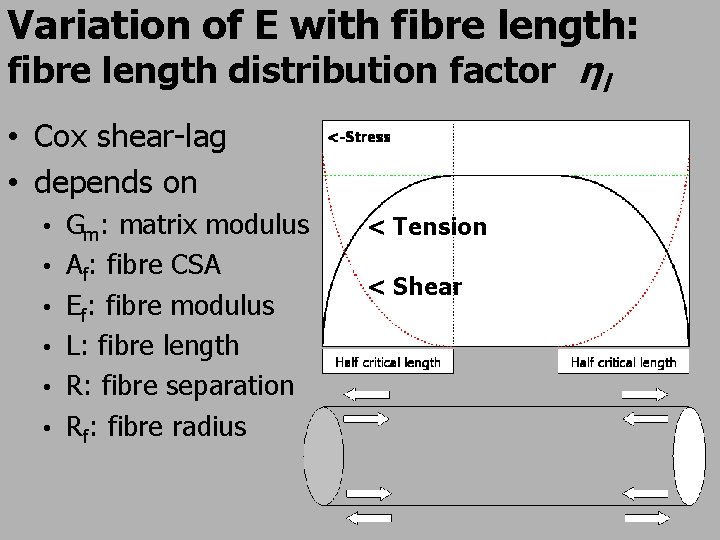
Variation of E with fibre length: fibre length distribution factor ηl • Cox shear-lag • depends on • • • Gm: matrix modulus Af: fibre CSA Ef: fibre modulus L: fibre length R: fibre separation Rf: fibre radius < Tension < Shear

Variation of E with fibre length: fibre length distribution factor ηl • Cox shear-lag equation: where • critical length:

Poisson’s ratio (isotropic: ν) • = - (strain normal to the applied stress) (strain parallel to the applied stress). • thermodynamic constraint restricts the values to -1 < < ½ for isotropic materials

Poisson’s ratio: beware !! • For orthotropic materials, not all authors use the same notation a. subscripts mastimulus* then response b. subscripts maresponse then stimulus*stimulus = driving force The following page uses stimulus then response: • 1= fibres • 2 = resin (UD) or fibre (WR) • 3 = resin

Poisson’s ratio (orthotropic: νij) • Maxwell’s reciprocal theorem • ν 12 E 2 = ν 21 E 1 • Lemprière constraint restricts the values of ν to (1 -ν 23ν 32), (1 -ν 13ν 31), (1 -ν 12ν 21), (1 -ν 12ν 21 -ν 13ν 31 -ν 23ν 32 -2ν 21ν 32ν 13) > 0 hence νij ≤ (Ei/Ej)1/2 and ν 21ν 23ν 13 < 1/2.

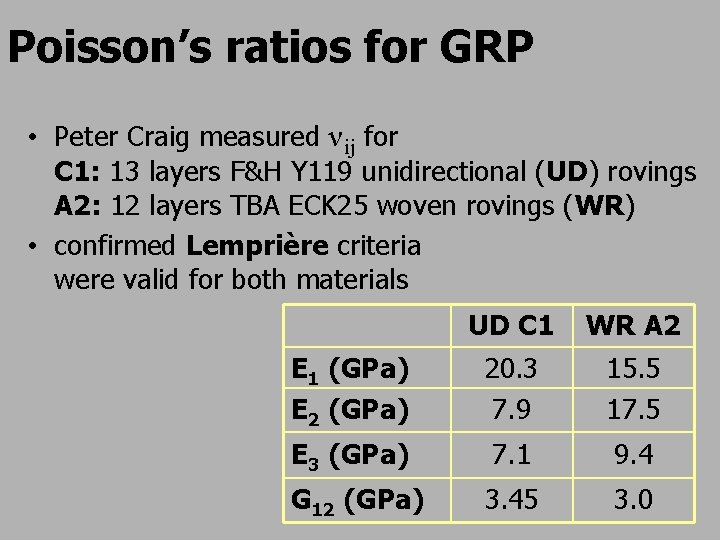
Poisson’s ratios for GRP • Peter Craig measured νij for C 1: 13 layers F&H Y 119 unidirectional (UD) rovings A 2: 12 layers TBA ECK 25 woven rovings (WR) • confirmed Lemprière criteria were valid for both materials UD C 1 WR A 2 E 1 (GPa) E 2 (GPa) 20. 3 7. 9 15. 5 17. 5 E 3 (GPa) 7. 1 9. 4 G 12 (GPa) 3. 45 3. 0

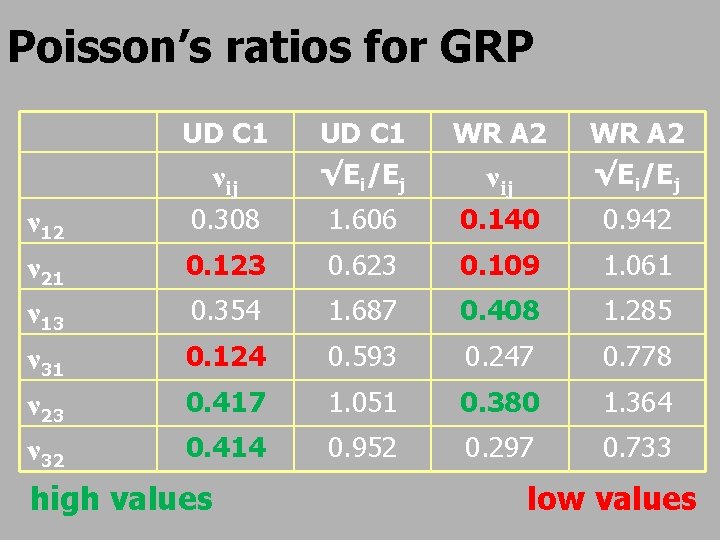
Poisson’s ratios for GRP UD C 1 ν 12 ν 21 ν 13 ν 31 ν 23 ν 32 WR A 2 νij UD C 1 √Ei/Ej νij WR A 2 √Ei/Ej 0. 308 1. 606 0. 140 0. 942 0. 123 0. 623 0. 109 1. 061 0. 354 1. 687 0. 408 1. 285 0. 124 0. 593 0. 247 0. 778 0. 417 1. 051 0. 380 1. 364 0. 414 0. 952 0. 297 0. 733 high values low values

Extreme values of νij • Dickerson and Di Martino (1966): orthotropic (cross-plied) boron/epoxy composites Poisson's ratios range from 0. 024 to 0. 878 • ± 25º laminate boron/epoxy composites Poisson's ratios range from -0. 414 to 1. 97 •

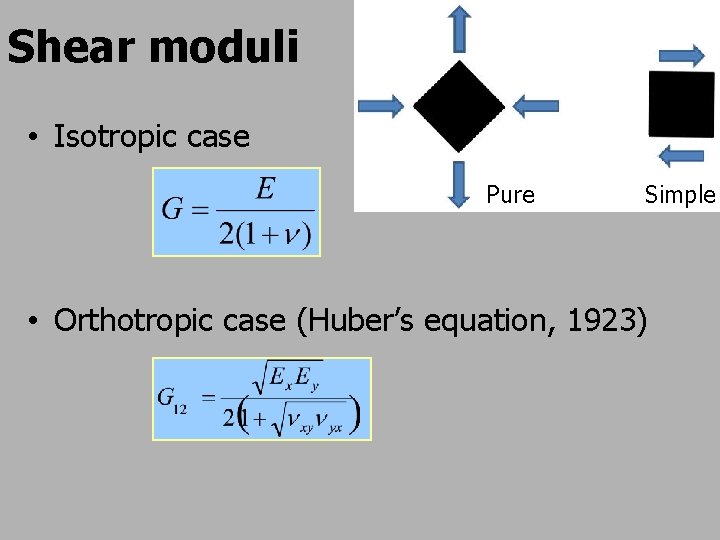
Shear moduli • Isotropic case Pure Simple • Orthotropic case (Huber’s equation, 1923)

Bulk modulus • Isotropic case • Orthotropic case

Negative Poisson’s ratio (auxetic) materials • Re-entrant or chiral structures

Summary • Young’s moduli • Poisson’s ratios, • including reentrant/chiral auxetics • Shear moduli • Bulk modulus