Elastic Collisions Momentum and Kinetic Energy An object
Elastic Collisions
![Momentum and Kinetic Energy ] An object in motion has a momentum based on](http://slidetodoc.com/presentation_image_h2/52c921c02705d008e72f8050f949927a/image-2.jpg "Momentum and Kinetic Energy ] An object in motion has a momentum based on")
Momentum and Kinetic Energy ] An object in motion has a momentum based on its mass and velocity. • p = mv ] The object also has kinetic energy. • K = ½ mv 2 = p 2 / 2 m
![Kinetic Energy at Collision m 1 ] Energy is conserved only for conservative forces.](http://slidetodoc.com/presentation_image_h2/52c921c02705d008e72f8050f949927a/image-3.jpg "Kinetic Energy at Collision m 1 ] Energy is conserved only for conservative forces.")
Kinetic Energy at Collision m 1 ] Energy is conserved only for conservative forces. v 1 i v 2 i m 2 Before: ] ] Internal forces may be nonconservative. The force at the collision is not always conservative. energy lost to heat v 1 f After: v 2 f
![Elastic Collision ] For conservative forces the energy is conserved. Elastic ] After the](http://slidetodoc.com/presentation_image_h2/52c921c02705d008e72f8050f949927a/image-4.jpg "Elastic Collision ] For conservative forces the energy is conserved. Elastic ] After the")
Elastic Collision ] For conservative forces the energy is conserved. Elastic ] After the collision of contact the potential energy is zero. ] The total kinetic energy is conserved – equal before and after the collision. ] This an elastic collision.
![Double Conservation ] ] Elastic collisions conserve both momentum and kinetic energy. Two equations](http://slidetodoc.com/presentation_image_h2/52c921c02705d008e72f8050f949927a/image-5.jpg "Double Conservation ] ] Elastic collisions conserve both momentum and kinetic energy. Two equations")
Double Conservation ] ] Elastic collisions conserve both momentum and kinetic energy. Two equations govern all elastic collisions. m 1 v 1 i m 1 m 2 v 2 i before v 1 f m 2 v 2 f after
![Head-on Collision ] An elastic head-on collision takes place in one dimension. v 1](http://slidetodoc.com/presentation_image_h2/52c921c02705d008e72f8050f949927a/image-6.jpg "Head-on Collision ] An elastic head-on collision takes place in one dimension. v 1")
Head-on Collision ] An elastic head-on collision takes place in one dimension. v 1 i v 2 i ] If the collision is not head-on, the force pair is in a different direction. v 1 i v 2 i m 1 m 2 force and velocity in a line m 1 m 2 force and velocity on different lines
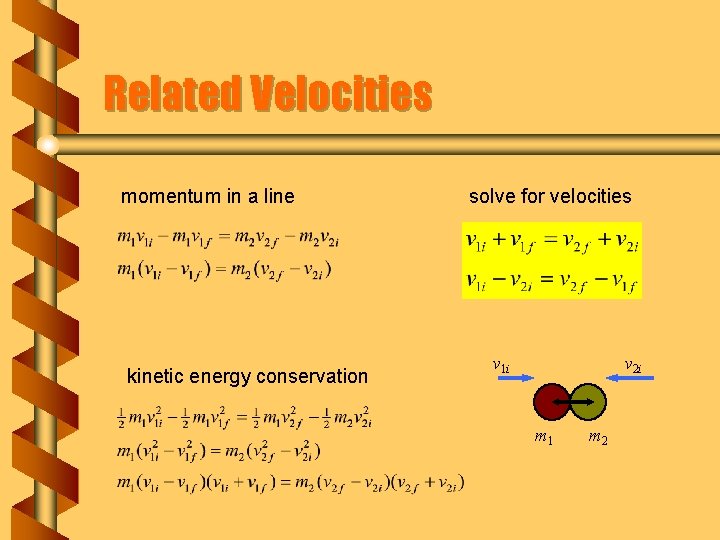
Related Velocities momentum in a line kinetic energy conservation solve for velocities v 1 i v 2 i m 1 m 2
![Equal Masses ] A 150 g ball moves at 1. 4 m/s. • The](http://slidetodoc.com/presentation_image_h2/52c921c02705d008e72f8050f949927a/image-8.jpg "Equal Masses ] A 150 g ball moves at 1. 4 m/s. • The")
Equal Masses ] A 150 g ball moves at 1. 4 m/s. • The momentum is 0. 21 kg m/s ] v 1 i m 1 It strikes an equal mass ball at rest. • • v 1 i = 1. 4 m/s v 2 i = 0 Therefore, v 1 f = 0 and v 2 f = v 1 i momentum: kinetic energy: m 2 m 1 m 2 v 2 f
![Striking a Heavy Mass ] ] Let m 1 << m 2, when a](http://slidetodoc.com/presentation_image_h2/52c921c02705d008e72f8050f949927a/image-9.jpg "Striking a Heavy Mass ] ] Let m 1 << m 2, when a")
Striking a Heavy Mass ] ] Let m 1 << m 2, when a golf ball momentum: bounces off the floor. The floor is at rest. kinetic energy: • v 2 i = 0 ] The final velocity is equal and opposite the initial velocity m 1 v 1 i v 1 f combined:
![Striking a Light Mass ] ] Let m 1 >> m 2, when a](http://slidetodoc.com/presentation_image_h2/52c921c02705d008e72f8050f949927a/image-10.jpg "Striking a Light Mass ] ] Let m 1 >> m 2, when a")
Striking a Light Mass ] ] Let m 1 >> m 2, when a car strikes a ball. The ball is at rest. • v 2 i = 0 ] For a very heavy m 1 , the final velocity of m 2 is twice the initial velocity of m 1. v 2 f m 2 v 1 i momentum: kinetic energy: combined:
- Slides: 10