Elaborazione di immagini Cenni Francesco AMATO framatounina it

Elaborazione di immagini Cenni Francesco AMATO – framato@unina. it ELABORAZIONE DEI SEGNALI E DATI BIOMEDICI – versione 1. 1 Marzo 2019 Corso di Laurea in Ingegneria Biomedica – DIETI- Uni. NA

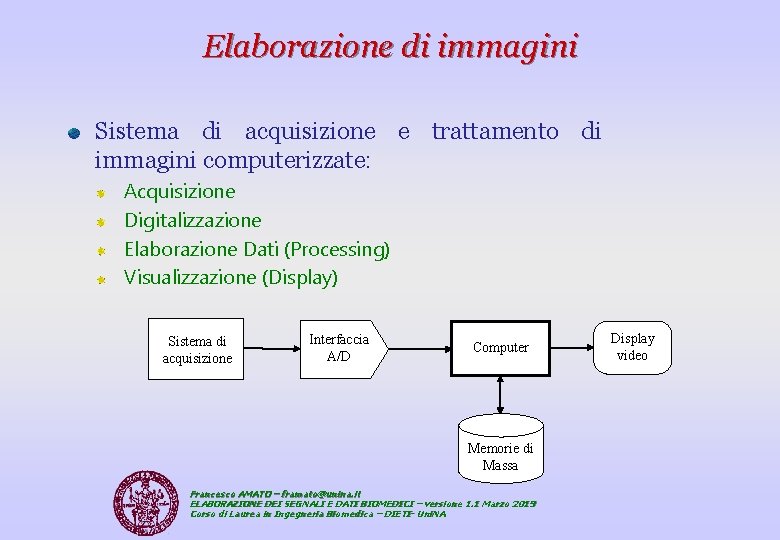
Elaborazione di immagini Sistema di acquisizione e trattamento di immagini computerizzate: Acquisizione Digitalizzazione Elaborazione Dati (Processing) Visualizzazione (Display) Sistema di acquisizione Interfaccia A/D Computer Memorie di Massa Francesco AMATO – framato@unina. it ELABORAZIONE DEI SEGNALI E DATI BIOMEDICI – versione 1. 1 Marzo 2019 Corso di Laurea in Ingegneria Biomedica – DIETI- Uni. NA Display video

1 Campionamento del segnale bidimensionale È possibile rappresentare una immagine in bianco e nero come una funzione a due dimensioni continua f(x, y), intensità luminosa o livello di grigio associato a x e y. Insieme di definizione di questa funzione è il dominio spaziale dell’immagine. Si può pensare di effettuare una operazione di campionamento e quantizzazione del segnale Campionamento spaziale. I campioni dell’immagine sono determinati tramite una moltiplicazione della funzione f(x, y) per una funzione di campionamento del tipo: δc(x, y) = Σn Σm δc (x-nΔx, y-mΔy) Δx e Δy passo di campionamento spaziale lungo l'asse x e l'asse y. Francesco AMATO – framato@unina. it ELABORAZIONE DEI SEGNALI E DATI BIOMEDICI – versione 1. 1 Marzo 2019 Corso di Laurea in Ingegneria Biomedica – DIETI- Uni. NA

2 Campionamento del segnale bidimensionale L’immagine campionata sarà esprimibile secondo la formula seguente: fc(x, y) = f(x, y)δc(x, y) = Σn Σm f(nΔx, mΔy) δc(x-nΔx, y-mΔy) Questa funzione risulta allora definita solo nei punti di campionamento (nΔx, mΔy); i valori così ottenuti f(nΔx, mΔy) sono detti campioni spaziali della funzione f(x, y). Δx Δy Francesco AMATO – framato@unina. it ELABORAZIONE DEI SEGNALI E DATI BIOMEDICI – versione 1. 1 Marzo 2019 Corso di Laurea in Ingegneria Biomedica – DIETI- Uni. NA

Campionamento del segnale bidimensionale 3 ωx ωy A ωx ωy B Francesco AMATO – framato@unina. it ELABORAZIONE DEI SEGNALI E DATI BIOMEDICI – versione 1. 1 Marzo 2019 Corso di Laurea in Ingegneria Biomedica – DIETI- Uni. NA

1 Quantizzazione e codifica binaria La quantizzazione consiste nell’associare ai singoli campioni spaziali f(n 1, n 2) di luminosità un numero, appartenente ad un intervallo numerico finito di livelli di grigio (Q) (risoluzione pari a 1/Q). I livelli possibili ai saranno compresi nell’intervallo: ao ≤ ai ≤ aq ao valore minimo (generalmente pari a zero), a q valore massimo. È possibile definire l’errore di quantizzazione normalizzato all’ampiezza massima aq come: q=aq/Q In definitiva l’immagine risulta trasformata in una matrice di numeri interi x(n 1, n 2). Francesco AMATO – framato@unina. it ELABORAZIONE DEI SEGNALI E DATI BIOMEDICI – versione 1. 1 Marzo 2019 Corso di Laurea in Ingegneria Biomedica – DIETI- Uni. NA

2 Quantizzazione e codifica binaria L’operazione di codifica binaria trasforma la luminosità in un numero finito di livelli, in genere, secondo potenze di 2: Q=2 m m numero di bit necessari a rappresentare il numero totale di livelli di grigio (Q). I campioni spaziali diventano parole di m simboli binari (1, 0) ognuno esprimibile dalla relazione: i = Σk ak 2 k (ak = 0 o 1). Esempio: m = 8 ed i = 109 = 0 • 27 + 1 • 26 + 1 • 25 + 0 • 24 + 1 • 23 + 1 • 22 + 0 • 21 + 1 • 20 0 1 1 Francesco AMATO – framato@unina. it ELABORAZIONE DEI SEGNALI E DATI BIOMEDICI – versione 1. 1 Marzo 2019 Corso di Laurea in Ingegneria Biomedica – DIETI- Uni. NA 0 1

Rapporto segnale rumore Francesco AMATO – framato@unina. it ELABORAZIONE DEI SEGNALI E DATI BIOMEDICI – versione 1. 1 Marzo 2019 Corso di Laurea in Ingegneria Biomedica – DIETI- Uni. NA

1 Qualità delle immagini mediche Nitidezza (Sharpness) Consiste principalmente nella capacità di un sistema di presentare (e dunque permettere di distinguere) i dettagli più fini di un immagine. Il deterioramento dei dettagli è principalmente dovuta alla risposta impulsiva dell’intero sistema di immagini, la cosiddetta Point Spread Function (PSF). PSF δ(s) Fourier Transform MTF Sistema di acquisizione s s Francesco AMATO – framato@unina. it ELABORAZIONE DEI SEGNALI E DATI BIOMEDICI – versione 1. 1 Marzo 2019 Corso di Laurea in Ingegneria Biomedica – DIETI- Uni. NA 1/s

2 Qualità delle immagini mediche La nitidezza è valutata dalla risoluzione spaziale dell'immagine (potere risolutivo), definita come la capacità dell'immagine di un sistema per immagini di distinguere due piccoli punti ad alto contrasto vicini tra loro. La risoluzione spaziale è determinata dalla più piccola distanza tra due punti distinguibili ad alto contrasto o dall’ampiezza della FWHM (Full Width at Half Maximum) o dal parametro LSF (il numero di linee distinguibili per centimetro) o dalla MTF (Modular Transfer Function). δ PSF Sistema di acquisizione s s Francesco AMATO – framato@unina. it ELABORAZIONE DEI SEGNALI E DATI BIOMEDICI – versione 1. 1 Marzo 2019 Corso di Laurea in Ingegneria Biomedica – DIETI- Uni. NA I I/2 FWHM s

3 Qualità delle immagini mediche Contrasto (Contrast) Possibilità di distinguere dettagli dell’immagine a bassa differenza di luminosità rispetto al fondo (background). Per valutare il contrasto di una immagine è usato il termine risoluzione di contrasto (contrast resolution) che è definito come la più piccola differenza di intensità distinguibile tra una piccola area dell’immagine (di specifica forma e grandezza) e lo sfondo (background). Il contrasto può essere quantificato dall’equazione: Francesco AMATO – framato@unina. it ELABORAZIONE DEI SEGNALI E DATI BIOMEDICI – versione 1. 1 Marzo 2019 Corso di Laurea in Ingegneria Biomedica – DIETI- Uni. NA

4 Qualità delle immagini mediche Rumore (Noise) Rumore di natura statistica e dipendente dal segnale, considerato additivo e bianco. Una valutazione del contenuto complessivo di rumore in un’immagine può essere derivato da: la deviazione standard dell’intensità del pixel in un area dell’immagine, dove il segnale è relativamente costante. la densità spettrale di potenza del rumore, valutata dalle componenti armoniche ad alta frequenza dell'immagine, dove prevale il rumore. Parametro generale di qualità di una immagine: Francesco AMATO – framato@unina. it ELABORAZIONE DEI SEGNALI E DATI BIOMEDICI – versione 1. 1 Marzo 2019 Corso di Laurea in Ingegneria Biomedica – DIETI- Uni. NA

1 Elaborazione delle immagini Image enhancement Modello generale di degradazione dell’immagine: y(n 1, n 2) = x(n 1, n 2) *h(n 1, n 2)+ d(n 1, n 2) Il termine di convoluzione sopprime le frequenze medio-alte dell'immagine producendo uno smussamento dei contorni (perdita di dettaglio). h(n 1, n 2) è la Point Spread Function. Il termine d(n 1, n 2) rappresenta il rumore. x(n 1, n 2) IMAGE h(n 1, n 2) P. S. F. y(n 1, n 2) d(n 1, n 2) noise Francesco AMATO – framato@unina. it ELABORAZIONE DEI SEGNALI E DATI BIOMEDICI – versione 1. 1 Marzo 2019 Corso di Laurea in Ingegneria Biomedica – DIETI- Uni. NA

2 Elaborazione delle immagini Image enhancement Categorie di tecniche per il miglioramento della qualità dell’immagine: Image Smoothing per diminuire il rumore Image Sharpening per diminuire lo sfocamento dell’immagine Manipolazione scala dei grigi per aumentare il contrasto Possiamo dividere le tecniche in due grandi categorie: LINEARI NON LINEARI per gli algoritmi lineari varranno tutte le regole più comunemente utilizzate per elaborare segnali digitali. Francesco AMATO – framato@unina. it ELABORAZIONE DEI SEGNALI E DATI BIOMEDICI – versione 1. 1 Marzo 2019 Corso di Laurea in Ingegneria Biomedica – DIETI- Uni. NA

1 Image smoothing - Media locale Caso monodimensionale 1 D 1 D Il processo di degradazione del segnale nel caso 1 D è: y(n)=x(n)*h(n) + d(n) = x'(n) + d(n) Detta hf(n) la risposta impulsiva del filtro, si ha y’(n)=y(n)*hf(n)= x'(n) *hf(n)+ d(n)*hf(n) Considerando come filtro hf(n) un Filtro FIR, si ha: Se il rumore è considerato bianco e a media nulla ci si aspetta che il suo valor medio tenda a zero; più grande sarà M più il secondo termine sarà prossimo a zero. M grande sopprimerà notevolmente anche il contenuto in alta frequenza del segnale. Francesco AMATO – framato@unina. it ELABORAZIONE DEI SEGNALI E DATI BIOMEDICI – versione 1. 1 Marzo 2019 Corso di Laurea in Ingegneria Biomedica – DIETI- Uni. NA

2 Image smoothing Media locale Caso 2 D Il processo di degradazione dell'immagine è: y(n 1, n 2) = x(n 1, n 2) * h(n 1, n 2) + d(n 1, n 2) Il processo di filtraggio : y’(n 1, n 2) = y(n 1, n 2) * lf(n 1, n 2) Considerando il filtro lf(n 1, n 2): L’equazione del filtro diventa: Francesco AMATO – framato@unina. it ELABORAZIONE DEI SEGNALI E DATI BIOMEDICI – versione 1. 1 Marzo 2019 Corso di Laurea in Ingegneria Biomedica – DIETI- Uni. NA

3 Image smoothing Media locale Supponendo M=3, l’equazione precedente ci indica che una matrice 3 x 3 (la cosiddetta Maschera - mask) si muove sull’intera immagine (che a sua volta è una matrice) calcolando localmente la convoluzione bidimensionale. Le maschere 3 x 3 più usate sono: SM 1 SM 2 SM 3 SM 4 Francesco AMATO – framato@unina. it ELABORAZIONE DEI SEGNALI E DATI BIOMEDICI – versione 1. 1 Marzo 2019 Corso di Laurea in Ingegneria Biomedica – DIETI- Uni. NA

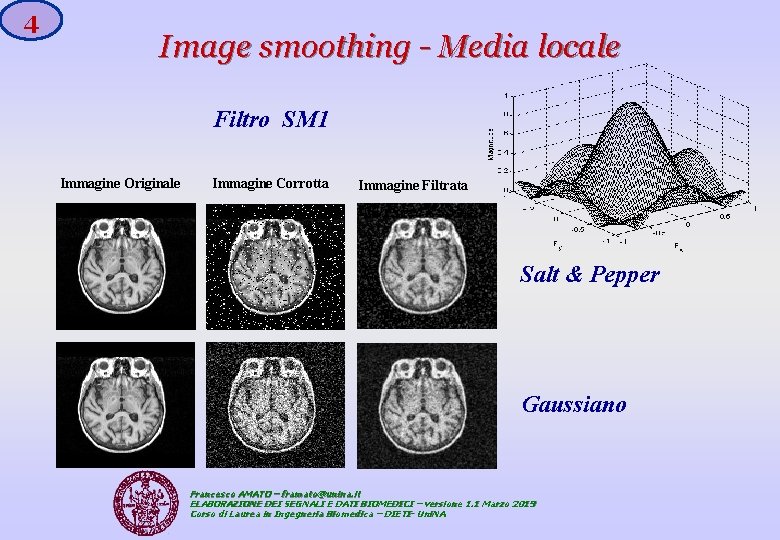
4 Image smoothing - Media locale Filtro SM 1 Immagine Originale Immagine Corrotta Immagine Filtrata Salt & Pepper Gaussiano Francesco AMATO – framato@unina. it ELABORAZIONE DEI SEGNALI E DATI BIOMEDICI – versione 1. 1 Marzo 2019 Corso di Laurea in Ingegneria Biomedica – DIETI- Uni. NA

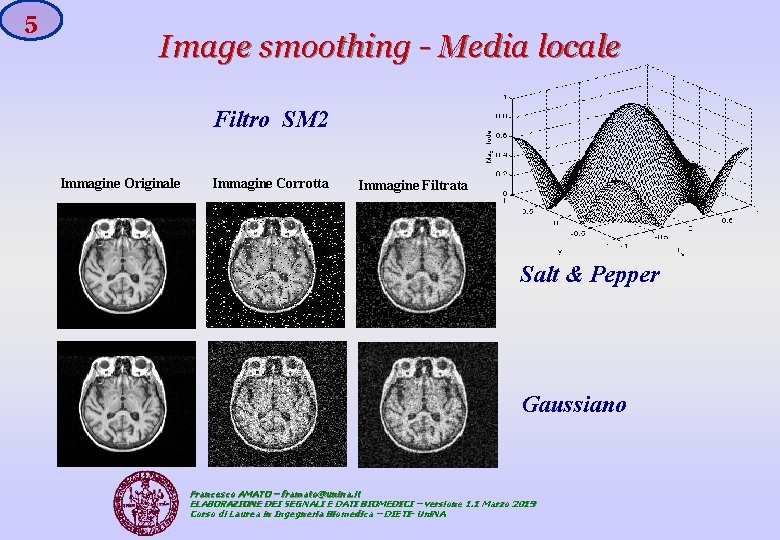
5 Image smoothing - Media locale Filtro SM 2 Immagine Originale Immagine Corrotta Immagine Filtrata Salt & Pepper Gaussiano Francesco AMATO – framato@unina. it ELABORAZIONE DEI SEGNALI E DATI BIOMEDICI – versione 1. 1 Marzo 2019 Corso di Laurea in Ingegneria Biomedica – DIETI- Uni. NA

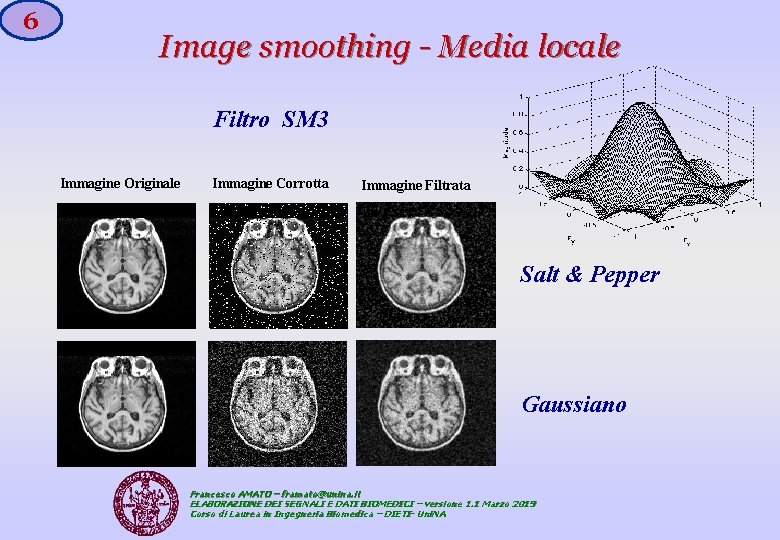
6 Image smoothing - Media locale Filtro SM 3 Immagine Originale Immagine Corrotta Immagine Filtrata Salt & Pepper Gaussiano Francesco AMATO – framato@unina. it ELABORAZIONE DEI SEGNALI E DATI BIOMEDICI – versione 1. 1 Marzo 2019 Corso di Laurea in Ingegneria Biomedica – DIETI- Uni. NA

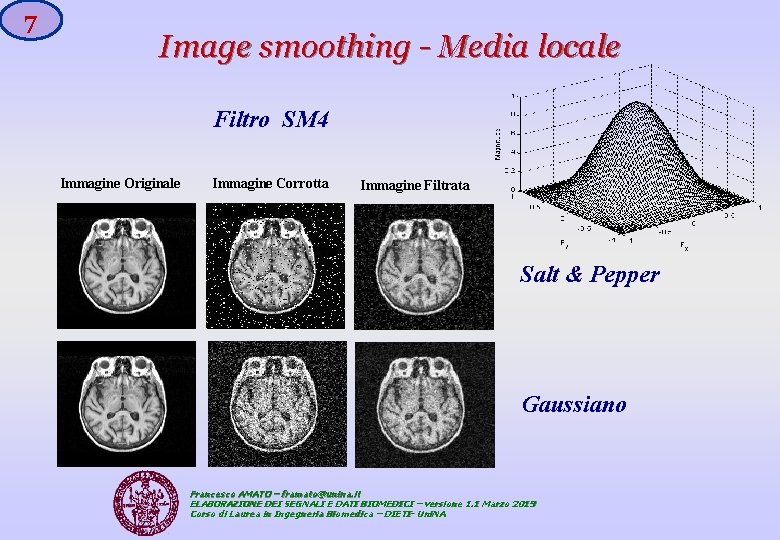
7 Image smoothing - Media locale Filtro SM 4 Immagine Originale Immagine Corrotta Immagine Filtrata Salt & Pepper Gaussiano Francesco AMATO – framato@unina. it ELABORAZIONE DEI SEGNALI E DATI BIOMEDICI – versione 1. 1 Marzo 2019 Corso di Laurea in Ingegneria Biomedica – DIETI- Uni. NA

1 Media locale selettiva – Filtri a mediana La mediana di n campioni (usualmente dispari) si ottiene ordinando i valori dei campioni in ordine crescente o decrescente e prelevando il termine centrale (che bipartisce la sequenza ordinata dei valori in due successioni di egual numero di termini, gli uni di valore inferiore alla mediana stessa, gli altri di valore superiore). Ad esempio consideriamo i 7 seguenti campioni: 18 26 23 14 21 28 25 la mediana si ottiene ordinando e prelevando il valore centrale 14 18 21 23 25 26 28 Francesco AMATO – framato@unina. it ELABORAZIONE DEI SEGNALI E DATI BIOMEDICI – versione 1. 1 Marzo 2019 Corso di Laurea in Ingegneria Biomedica – DIETI- Uni. NA

2 Media locale selettiva – Filtri a mediana A - segnale originario B – segnale filtrato con filtro MA 1 D L=3 C – segnale filtrato con filtro a mediana L=3 Francesco AMATO – framato@unina. it ELABORAZIONE DEI SEGNALI E DATI BIOMEDICI – versione 1. 1 Marzo 2019 Corso di Laurea in Ingegneria Biomedica – DIETI- Uni. NA

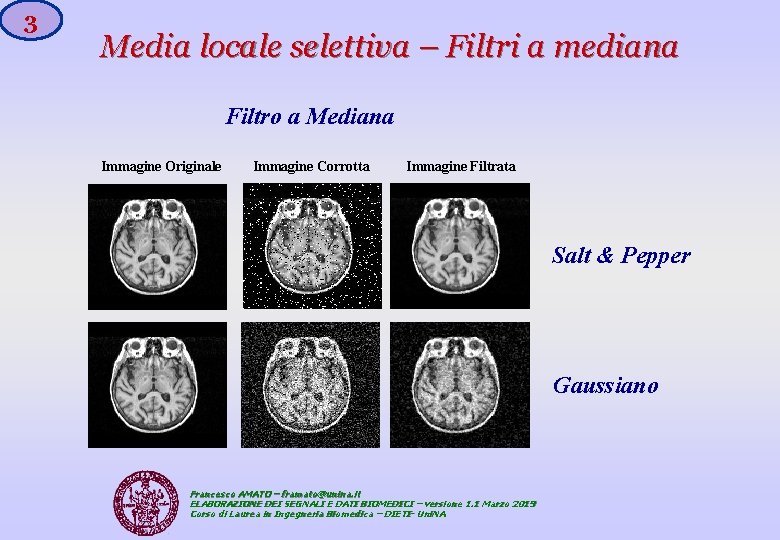
3 Media locale selettiva – Filtri a mediana Filtro a Mediana Immagine Originale Immagine Corrotta Immagine Filtrata Salt & Pepper Gaussiano Francesco AMATO – framato@unina. it ELABORAZIONE DEI SEGNALI E DATI BIOMEDICI – versione 1. 1 Marzo 2019 Corso di Laurea in Ingegneria Biomedica – DIETI- Uni. NA

Image sharpening Vanno sotto il nome di image sharpening le tecniche impiegate per ridurre lo sfuocamento (image blurring) di una immagine dovuto alla Point Spread Function (PSF) del processo di formazione dell’immagine stessa. Ricordiamo che il risultato di questo sfocamento dell’immagine consiste nella perdita di dettaglio dell’immagine e della chiarezza dei contorni, dunque in una soppressione delle frequenze medio-alte. È ovvio quindi che le tecniche di image sharpening (o deblurring) compiano l’operazione di esaltare le alte frequenze, cioè si tratta di un filtraggio passaalto. Comunque si deve esercitare cautela nello scegliere l’intensità di filtraggio passa-alto da applicare poiché il rumore dell’immagine risiede, particolarmente, nelle alte frequenze dello spettro dell'immagine. In questa zona l’ampiezza dello spettro di potenza del rumore può essere comparabile (se non superiore) a quello del segnale, dunque, un filtraggio passa-alto può avere l’effetto negativo di incrementare notevolmente il rumore. Così, usualmente, l'image sharpening può essere applicato dopo che sia stata effettuata una riduzione del rumore oppure in immagini dove il rapporto segnale-rumore sia alto. Francesco AMATO – framato@unina. it ELABORAZIONE DEI SEGNALI E DATI BIOMEDICI – versione 1. 1 Marzo 2019 Corso di Laurea in Ingegneria Biomedica – DIETI- Uni. NA

1 Filtri derivatori: Laplaciani Nel caso monodimensionale, il filtro derivatore è descritto dall’equazione: y(n)=[x(n+1)-x(n)] Consideriamo ora la matrice: dove con v 1, v 2, v 3 e v 4 sono stati indicati i vicini del punto x; Considerando ora le differenze: A 1=v 1 -x; A 2=v 2 -x; A 3=v 3 -x; A 4=v 4 -x Volendo calcolare la derivata bidimensionale, una sua semplice stima è data dalla somma delle 4 precedenti differenze: y=A 1+A 2+A 3+A 4=v 1+v 2+v 3+v 4 -4 x Francesco AMATO – framato@unina. it ELABORAZIONE DEI SEGNALI E DATI BIOMEDICI – versione 1. 1 Marzo 2019 Corso di Laurea in Ingegneria Biomedica – DIETI- Uni. NA

Filtri derivatori: Laplaciani 2 Ordinando diversamente i vari termini, si ha: dove Δ 2 H e Δ 2 V sono le derivate seconde orizzontali e verticali, ovvero, l’operatore Laplaciano nella direzione orizzontale e verticale. Questa è la ragione per cui il filtro descritto è usualmente denominato Filtro Laplaciano. Più formalmente tale filtro può essere descritto come dove Francesco AMATO – framato@unina. it ELABORAZIONE DEI SEGNALI E DATI BIOMEDICI – versione 1. 1 Marzo 2019 Corso di Laurea in Ingegneria Biomedica – DIETI- Uni. NA

3 Filtri derivatori: Laplaciani Se coinvolgiamo più punti di una immagine possiamo disegnare più maschere Laplaciane. Le maschere popolari sono: Usando questi filtri possiamo imbatterci nel caso in cui vi siano risultati negativi. Normalmente, i livelli di grigio assumono valori tutti positivi, per cui non è possibile assegnare ad un pixel un valore negativo. In una tale evenienza si usa assegnare, per convenzione, a questo pixel il valore 0, ovvero il più piccolo valore possibile. In formule: Francesco AMATO – framato@unina. it ELABORAZIONE DEI SEGNALI E DATI BIOMEDICI – versione 1. 1 Marzo 2019 Corso di Laurea in Ingegneria Biomedica – DIETI- Uni. NA

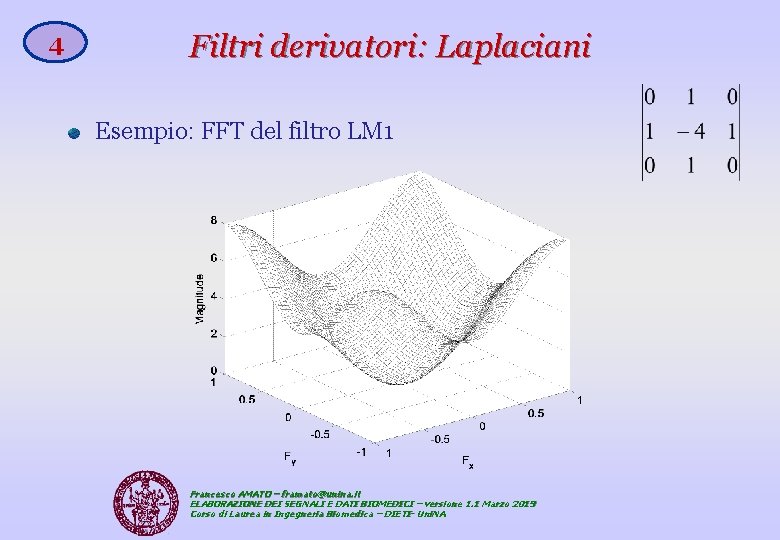
4 Filtri derivatori: Laplaciani Esempio: FFT del filtro LM 1 Francesco AMATO – framato@unina. it ELABORAZIONE DEI SEGNALI E DATI BIOMEDICI – versione 1. 1 Marzo 2019 Corso di Laurea in Ingegneria Biomedica – DIETI- Uni. NA

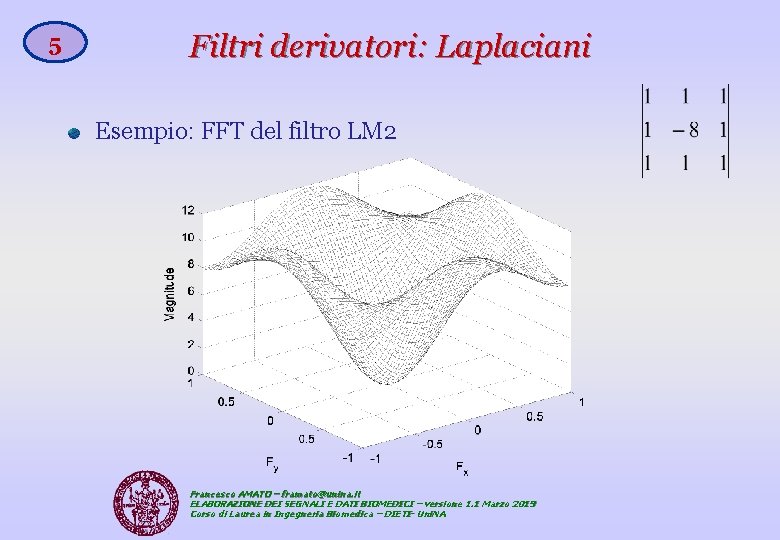
5 Filtri derivatori: Laplaciani Esempio: FFT del filtro LM 2 Francesco AMATO – framato@unina. it ELABORAZIONE DEI SEGNALI E DATI BIOMEDICI – versione 1. 1 Marzo 2019 Corso di Laurea in Ingegneria Biomedica – DIETI- Uni. NA

6 Filtri derivatori: Laplaciani Esempio: FFT del filtro LM 3 Francesco AMATO – framato@unina. it ELABORAZIONE DEI SEGNALI E DATI BIOMEDICI – versione 1. 1 Marzo 2019 Corso di Laurea in Ingegneria Biomedica – DIETI- Uni. NA

7 Filtri derivatori: Laplaciani Filtro LM 1 Immagine Originale Immagine filtrata Filtro LM 2 Immagine Originale Immagine filtrata Francesco AMATO – framato@unina. it ELABORAZIONE DEI SEGNALI E DATI BIOMEDICI – versione 1. 1 Marzo 2019 Corso di Laurea in Ingegneria Biomedica – DIETI- Uni. NA

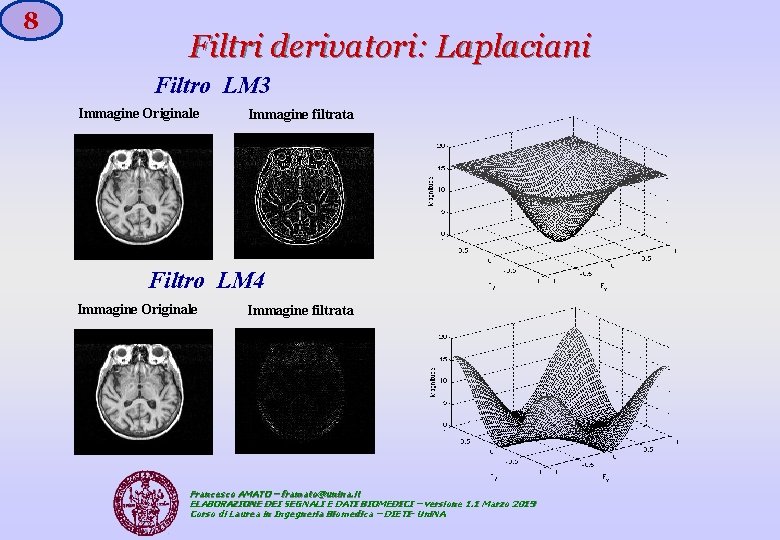
8 Filtri derivatori: Laplaciani Filtro LM 3 Immagine Originale Immagine filtrata Filtro LM 4 Immagine Originale Immagine filtrata Francesco AMATO – framato@unina. it ELABORAZIONE DEI SEGNALI E DATI BIOMEDICI – versione 1. 1 Marzo 2019 Corso di Laurea in Ingegneria Biomedica – DIETI- Uni. NA

Tecniche di manipolazione della scala dei grigi Vanno sotto questo nome alcune tecniche per il miglioramento della qualità di immagine che, sebbene siano di semplice e facile implementazione, forniscono eccellenti risultati. Esse cercano di affrontare il problema che in molte immagini mediche i valori della scala dei grigi effettivamente usati sono ben lungi da essere tutti quelli disponibili; usando poi sul monitor tutto il range possibile si ottiene l’effetto finale di diminuire il contrasto visibile. Ci sono, fondamentalmente, due tipi di tecniche di manipolazione della scala dei grigi a) Tecniche di Finestramento (Windowing Techniques) b) Tecniche di Modificazione dell’lstogramma (Histogram Modification) Francesco AMATO – framato@unina. it ELABORAZIONE DEI SEGNALI E DATI BIOMEDICI – versione 1. 1 Marzo 2019 Corso di Laurea in Ingegneria Biomedica – DIETI- Uni. NA

Tecniche di finestramento (Windowing Techniques) Principio del windowing livelli di quantizzazione dell’immagine 28=256 (V 1. . . V 256) livelli di grigio disponibili sul display 26=64 (Gl. . . G 64) L’algoritmo che calcola il livello di grigio del video (Gm) per ogni valore di grigio dell’immagine (Vm) del subrange selezionato [Va, Vb] è: Francesco AMATO – framato@unina. it ELABORAZIONE DEI SEGNALI E DATI BIOMEDICI – versione 1. 1 Marzo 2019 Corso di Laurea in Ingegneria Biomedica – DIETI- Uni. NA

1 Tecniche di equalizzazione dell’istogramma Si chiama istogramma il grafico che evidenzia il numero di pixel che assumono un determinato livello di grigio in funzione dei livelli di grigio disponibili. L’istogramma riporta in ascissa i livelli di grigio disponibili ed in ordinata il numero dei pixel dell’immagine che assumono un determinato livello di grigio. Francesco AMATO – framato@unina. it ELABORAZIONE DEI SEGNALI E DATI BIOMEDICI – versione 1. 1 Marzo 2019 Corso di Laurea in Ingegneria Biomedica – DIETI- Uni. NA

2 Tecniche di equalizzazione dell’istogramma Le tecniche di modificazione dell’istogramma cercano di aumentare il contrasto dell’immagine alterandone l’istogramma. L’istogramma risultante da tale processo può avere un ugual numero di pixel per livello di grigio “Procedura di Equalizzazione dell’Istogramma”. Sia X una variabile aleatoria assolutamente continua di livelli di grigio a≤X≤b e sia FX(x)=Prob(X≤x) la sua funzione di distribuzione cumulativa di probabilità. La variabile aleatoria Y=FX(x) risulterà avere la distribuzione: Y è dunque una variabile aleatoria UNIFORME. In pratica non si otterrà un istogramma piatto ma uno ad esso approssimabile. Francesco AMATO – framato@unina. it ELABORAZIONE DEI SEGNALI E DATI BIOMEDICI – versione 1. 1 Marzo 2019 Corso di Laurea in Ingegneria Biomedica – DIETI- Uni. NA

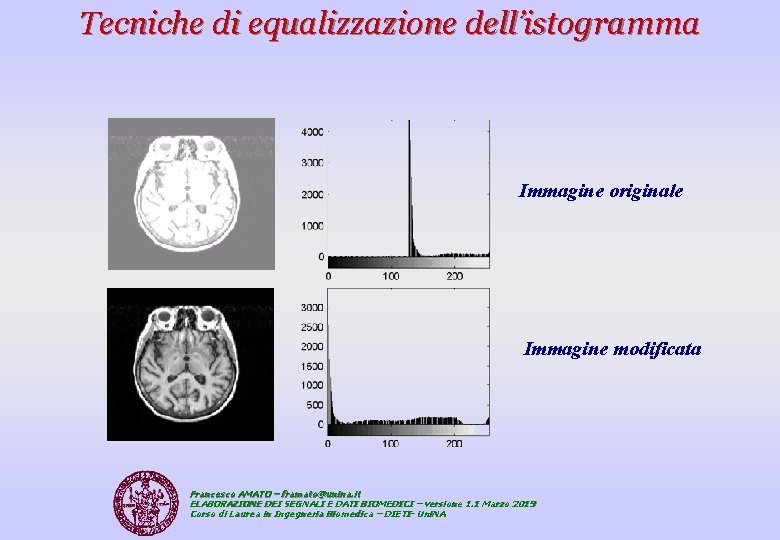
Tecniche di equalizzazione dell’istogramma Immagine originale Immagine modificata Francesco AMATO – framato@unina. it ELABORAZIONE DEI SEGNALI E DATI BIOMEDICI – versione 1. 1 Marzo 2019 Corso di Laurea in Ingegneria Biomedica – DIETI- Uni. NA