Elaboracin de grficas Es una grfica de reas

Elaboración de gráficas

Es una gráfica de áreas en donde en la escala horizontal se representan los intervalos de clase de los datos y en la escala vertical se ubican las frecuencias o frecuencias relativas. El área contenida en cada una de las celdas corresponde a los valores de frecuencia, por lo que todas las celdas se elaboran del mismo ancho y se dibujan de manera adyacente. Histogramas

Para poder elaborar un histograma necesitamos tener con anterioridad una distribución de frecuencia de los datos. Por ejemplo: Fuente. Ejercicio para la clase de 2º. D y 2º. E

• Determinar la unidad de medida utilizada en los intervalos de clase. • Para esto restamos el límite superior del primer intervalo con el límite inferior del segundo intervalo de clase. El límite superior del primer intervalo es 19 El límite inferior del segundo intervalo es 20 Por lo tanto la unidad de medida (lo que incrementa entre y el otro) es 1. un intervalo Esta unidad puede ser cualquier número, 1, 100, 5, 0. 1, 0. 01, todo es en función de la forma en la que estamos midiendo nuestra variable. Determinar la unidad de medida

Calcular los límites reales de los intervalos Aplicamos la fórmula para los límites reales en una medición con la diferencia de que disminuiremos la mitad de la unidad de medición al límite inferior del intervalo y le aumentamos la mitad de la unidad de medición al límite superior. Intervalo: 10 a 19 Valor menor del intervalo Unidad de medida Límite real inferior L. R. I = X - ( U. M. /2 )= 10 – (1/2)= 10 -(0. 5)=9. 5 Valor mayor del intervalo Unidad de medida Límite real superior L. R. S = X + ( U. M. /2 )= 19+(1/2)=19+(0. 5)=19. 5 *LRI: Límite real inferior del intervalo ~LRS: Límite real superior del intervalo Límites reales del Intervalo: 10 a 19: 9. 5 a 19. 5

y así sucesivamente. El resultado final será: Intervalos iniciales

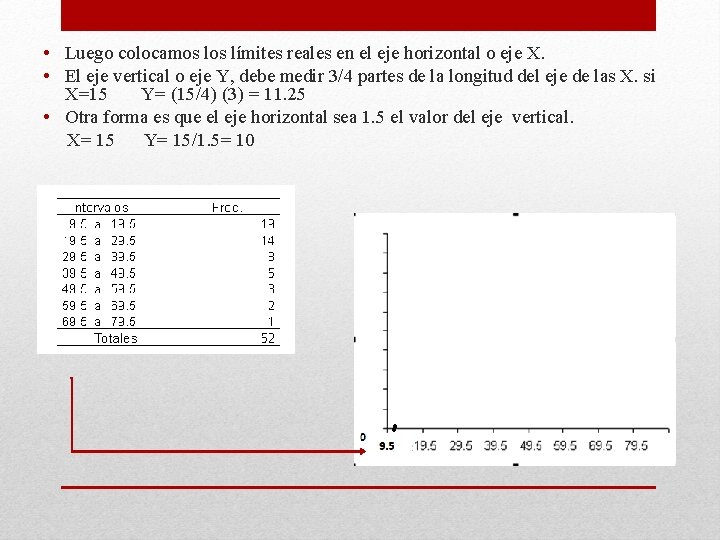
• Luego colocamos límites reales en el eje horizontal o eje X. • El eje vertical o eje Y, debe medir 3/4 partes de la longitud del eje de las X. si X=15 Y= (15/4) (3) = 11. 25 • Otra forma es que el eje horizontal sea 1. 5 el valor del eje vertical. X= 15 Y= 15/1. 5= 10

• • Luego ubicamos nuestra frecuencia más alta y la utilizamos como guía para el valor máximo en el eje de las Y. En este ejemplo nuestra frecuencia máxima es de 19, por lo que ubicamos el 20 como el valor más alto en el eje vertical. Luego ubicamos el resto de valores de manera proporcional.

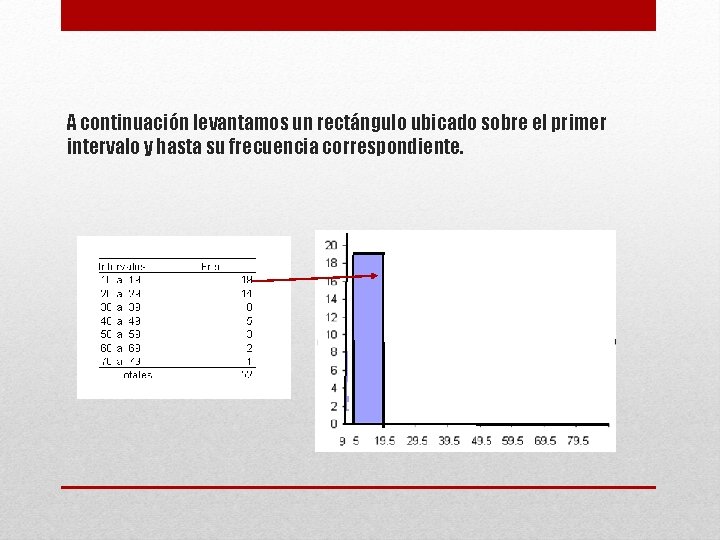
A continuación levantamos un rectángulo ubicado sobre el primer intervalo y hasta su frecuencia correspondiente.

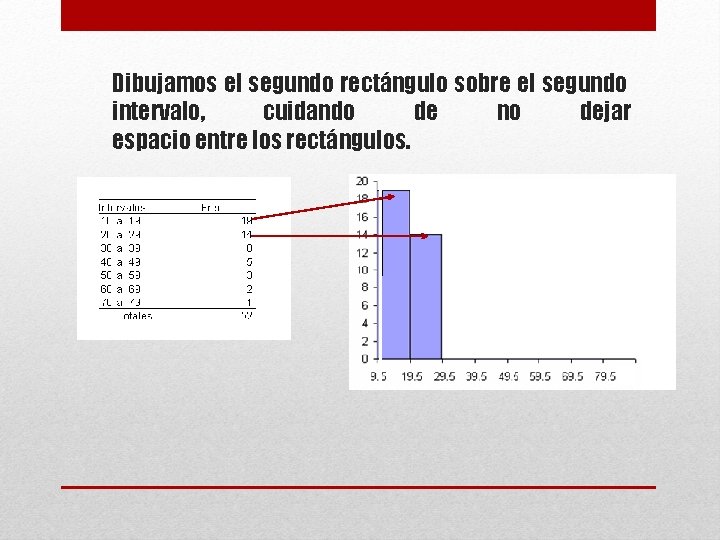
Dibujamos el segundo rectángulo sobre el segundo intervalo, cuidando de no dejar espacio entre los rectángulos.

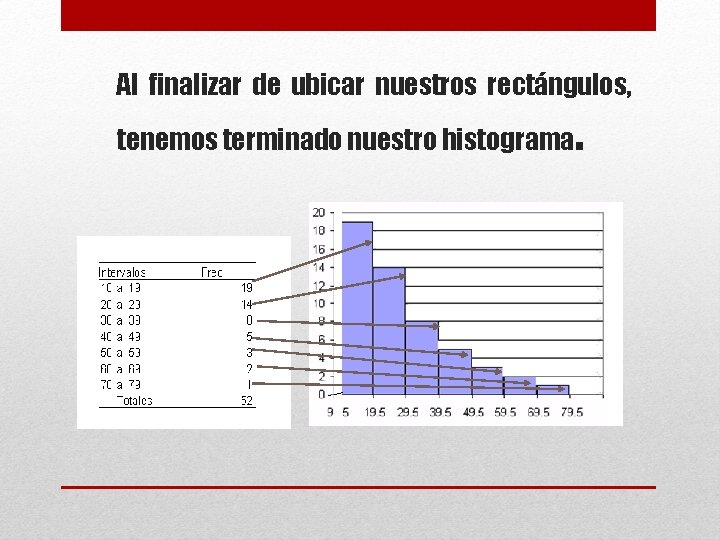
Al finalizar de ubicar nuestros rectángulos, tenemos terminado nuestro histograma .

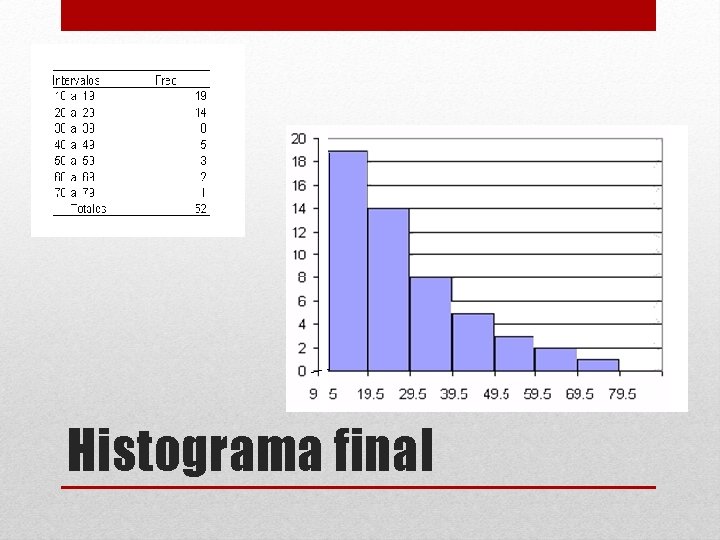
Histograma final

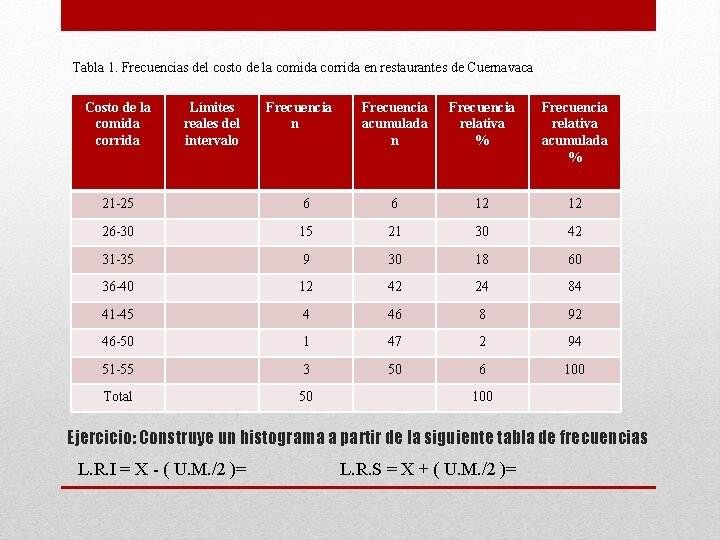
Tabla 1. Frecuencias del costo de la comida corrida en restaurantes de Cuernavaca Costo de la comida corrida Límites reales del intervalo Frecuencia n Frecuencia acumulada n Frecuencia relativa % Frecuencia relativa acumulada % 21 -25 6 6 12 12 26 -30 15 21 30 42 31 -35 9 30 18 60 36 -40 12 42 24 84 41 -45 4 46 8 92 46 -50 1 47 2 94 51 -55 3 50 6 100 Total 50 100 Ejercicio: Construye un histograma a partir de la siguiente tabla de frecuencias L. R. I = X - ( U. M. /2 )= L. R. S = X + ( U. M. /2 )=

• El polígono de frecuencias es una gráfica de áreas que utiliza segmentos lineales conectados a puntos que se localizan directamente por encima de los valores de las marcas de clase. Las alturas de los puntos corresponden a las frecuencias de clase, en tanto que los segmentos lineales se extienden hacia la derecha y la izquierda a una marca de clase extra en cada sentido, de manera que la gráfica inicia y termina sobre el eje horizontal. Polígonos de frecuencia

• Para poder elaborar un polígono de frecuencias necesitamos tener con anterioridad una distribución de frecuencia de los datos. Por ejemplo: Elaboración del polígono de frecuencias

Elaboración del polígono de frecuencias • Debemos obtener la marca de clase de cada intervalo. Esto es el punto medio de cada uno de los intervalos. Lo obtenemos sumando los límites aparentes inferior y superior del primer intervalo y dividiendo el resultado entre de dos: Límite inferior del intervalo [ (LIA + LSA) / 2 ]. Límite superior del intervalo Así en nuestro ejemplo, la marca de clase del primer intervalo sería: (10+19) /2 = 14. 5

• Agregamos una marca de clase o punto medio anterior y una marca de clase posterior. El resultado será: Clase o punto medio anterior Clase o punto medio posterior

Ubicamos las marcas de clase o puntos medios en el eje horizontal, y en el eje vertical (que debe medir 3/4 partes de la longitud total del eje horizontal) ubicamos la frecuencia máxima.

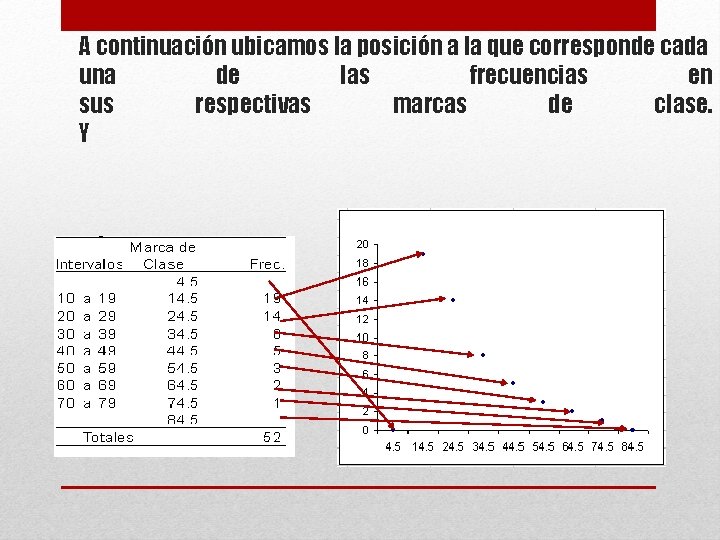
A continuación ubicamos la posición a la que corresponde cada una de las frecuencias en sus respectivas marcas de clase. Y

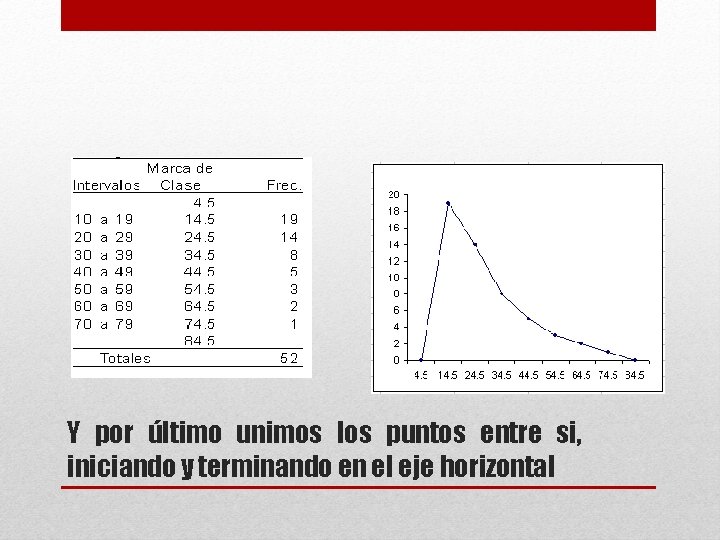
Y por último unimos los puntos entre si, iniciando y terminando en el eje horizontal

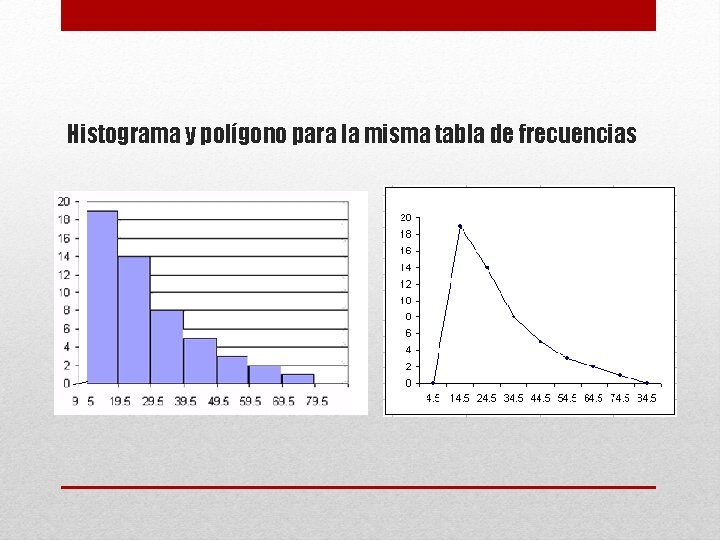
Histograma y polígono para la misma tabla de frecuencias

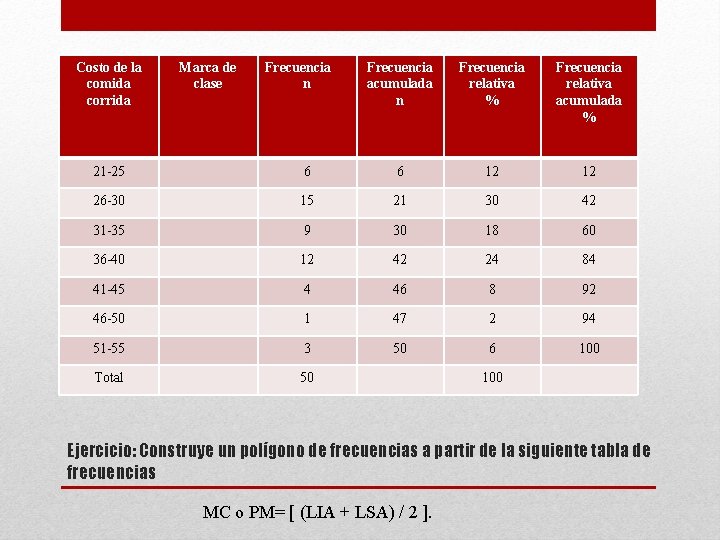
Costo de la comida corrida Marca de clase Frecuencia n Frecuencia acumulada n Frecuencia relativa % Frecuencia relativa acumulada % 21 -25 6 6 12 12 26 -30 15 21 30 42 31 -35 9 30 18 60 36 -40 12 42 24 84 41 -45 4 46 8 92 46 -50 1 47 2 94 51 -55 3 50 6 100 Total 50 100 Ejercicio: Construye un polígono de frecuencias a partir de la siguiente tabla de frecuencias MC o PM= [ (LIA + LSA) / 2 ].

A partir de los siguientes datos construye: • • • Una tabla de frecuencias con los siguientes datos: Frecuencia absoluta y acumulada Frecuencia relativa y frecuencia relativa acumulada Identifica los límites reales del intervalo Identifica las marcas de clase para cada intervalo Construye un histograma y un polígono de frecuencias. Ejercicio: En un hospital se desea hacer un estudio sobre los pesos de un grupo de niños. Para ello, se recogen los datos de 40 pacientes y se tiene: n=40 30. 2 35. 7 41. 2 41. 6 35. 7 33. 0 29. 9 33. 1 38. 0 41. 5 40. 1 37. 8 33. 9 37. 6 35. 2 38. 5 32. 0 29. 5 27. 7 28. 8 34. 0 46. 0 43. 5 36. 5 33. 5 31. 6 26. 9 31. 2 45. 2 41. 3 39. 1 41. 6 42. 2 44. 5 41. 3 31. 2 31. 7 26. 9 33. 1 39. 5

PASOS A SEGUIR 1. 2. 3. 4. 5. 6. 7. 8. 9. Identificar número total de observaciones Valor máximo y valor mínimo Ordenar los valores de mínimo a máximo Estimar el rango (R) (diferencia entre valor máximo y mínimo) Definir el número de intervalos (K) con la regla de Sturges K= 1+3. 322(log n) Calcular la amplitud del intervalo R/K= Construir la tabla de frecuencias (Frecuencia absoluta, acumulada, frecuencia relativa y frecuencia relativa acumulada) Identificar los límites reales del intervalo L. R. I = X - ( U. M. /2 )= L. R. S = X + ( U. M. /2 )= Identificar las marcas de clase [ (LIA + LSA) / 2 ]. 10. Armar histograma y polígono Ojo: Se utilizan los valores mínimo y máximo del intervalo, no los límites reales

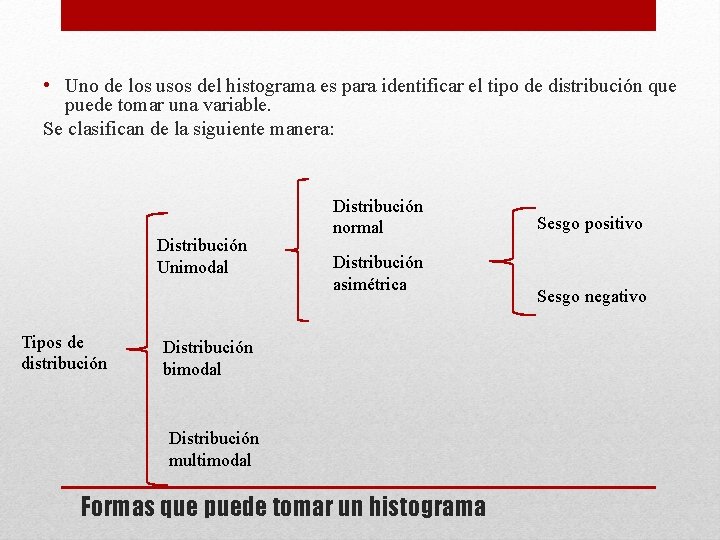
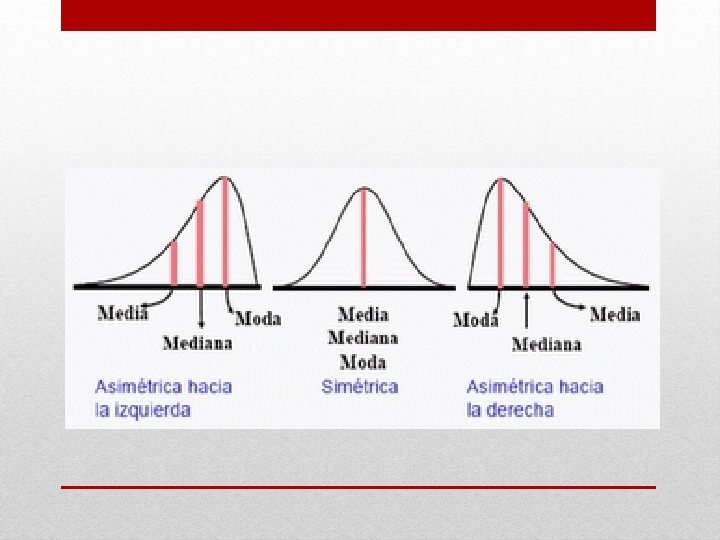
• Uno de los usos del histograma es para identificar el tipo de distribución que puede tomar una variable. Se clasifican de la siguiente manera: Distribución Unimodal Tipos de distribución Distribución normal Distribución asimétrica Distribución bimodal Distribución multimodal Formas que puede tomar un histograma Sesgo positivo Sesgo negativo

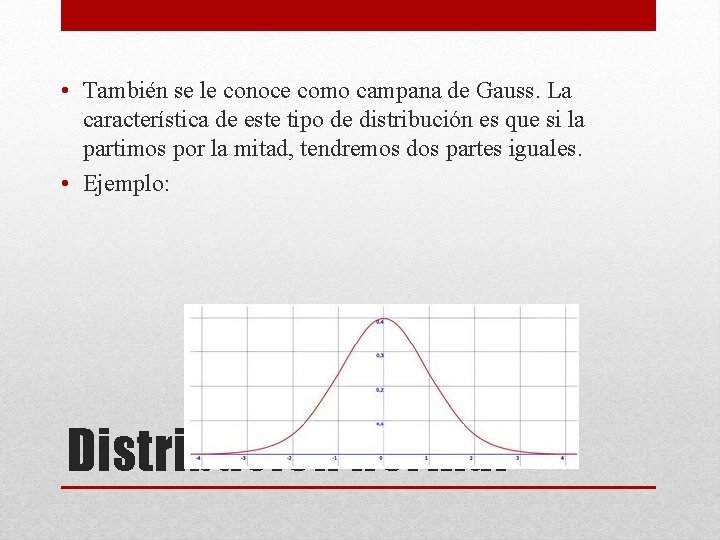
• También se le conoce como campana de Gauss. La característica de este tipo de distribución es que si la partimos por la mitad, tendremos dos partes iguales. • Ejemplo: Distribución normal

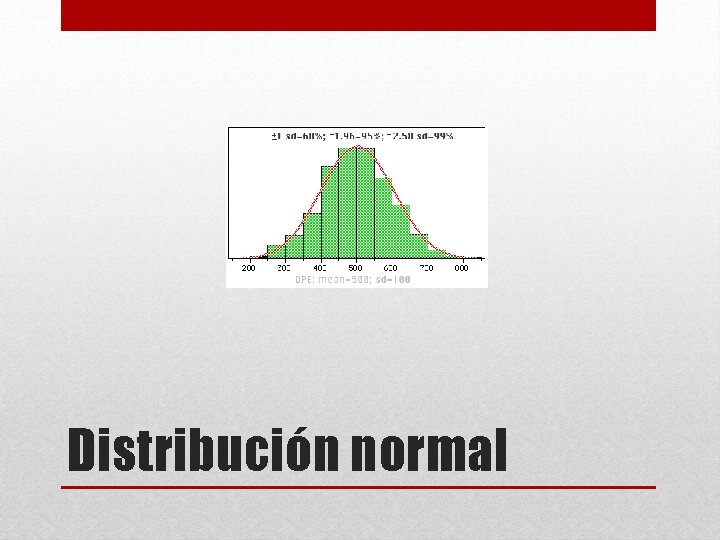
Distribución normal

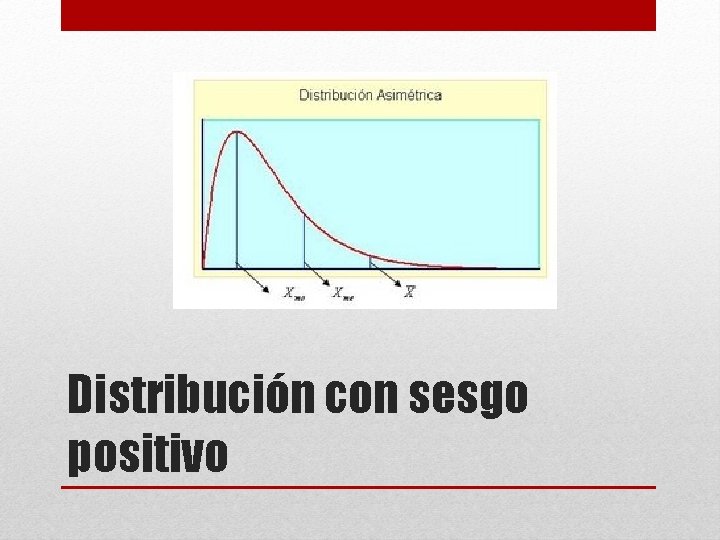
Distribución con sesgo positivo

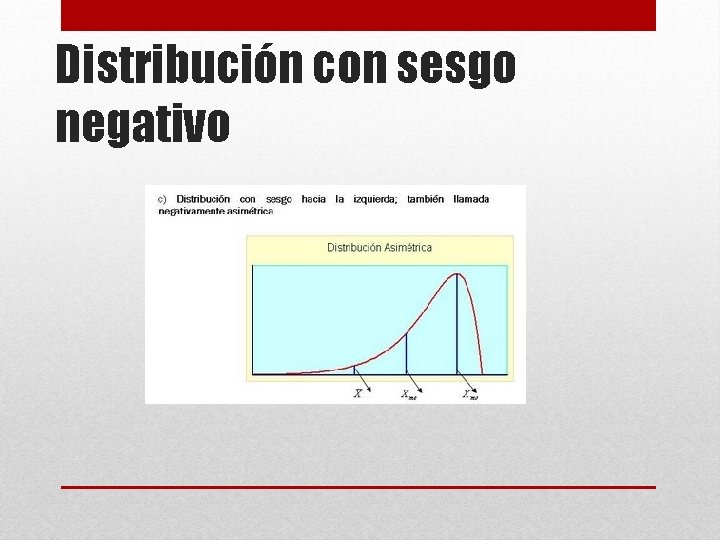
Distribución con sesgo negativo

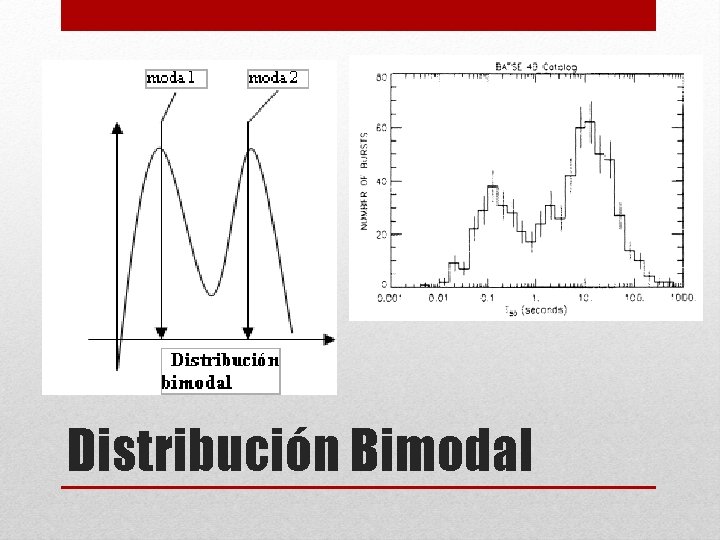
Distribución Bimodal

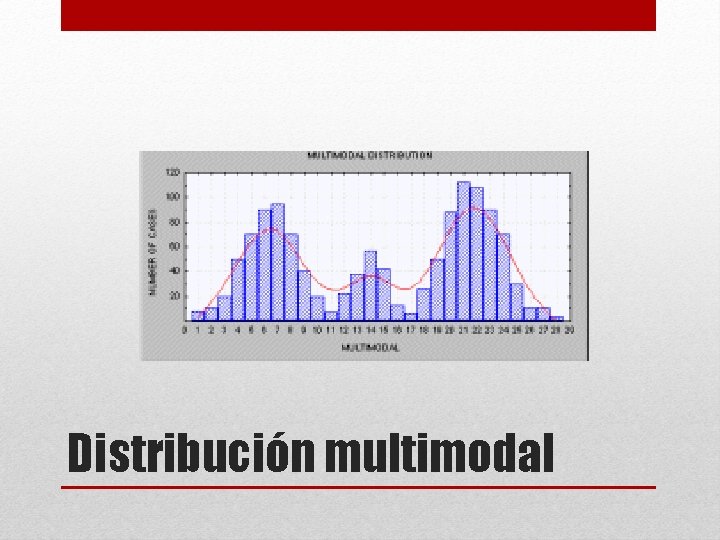
Distribución multimodal

Ejercicio • De las gráficas que has elaborado hasta ahora, identifica a que tipo de distribución pertenece