EKT 124 DIGITAL ELECTRONICS 1 CHAPTER 2 Digital













- Slides: 29

EKT 124 DIGITAL ELECTRONICS 1 CHAPTER 2 Digital Combinational Logic/Arithmetic Circuits

Digital Combinational Logic/Arithmetic Circuits q q q Arithmetic § Adder/Subtractor Converters § Decoder/Encoder/Comparator § Multiplexer/ Demultiplexer Parity Circuits § Generators § Checkers

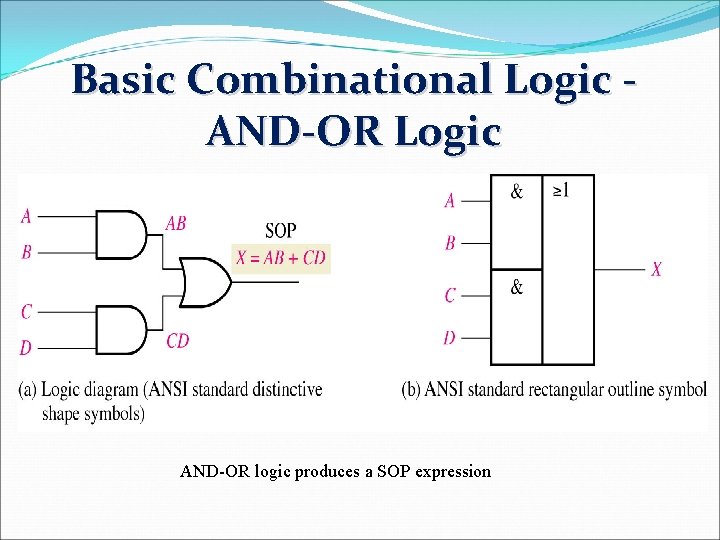
Basic Combinational Logic AND-OR logic produces a SOP expression

Basic Combinational Logic AND-OR Logic A 0 0 0 0 1 1 1 1 INPUTS B C 0 0 0 0 0 1 0 1 1 1 1 D 0 1 0 1 AB 0 0 0 1 1 CD 0 0 0 1 OUTPUT X 0 0 0 1 1 1 For a 4 -input AND-OR logic circuit, output X is HIGH(1) if both input A and input B are HIGH(1) or both input C and input D are HIGH(1).

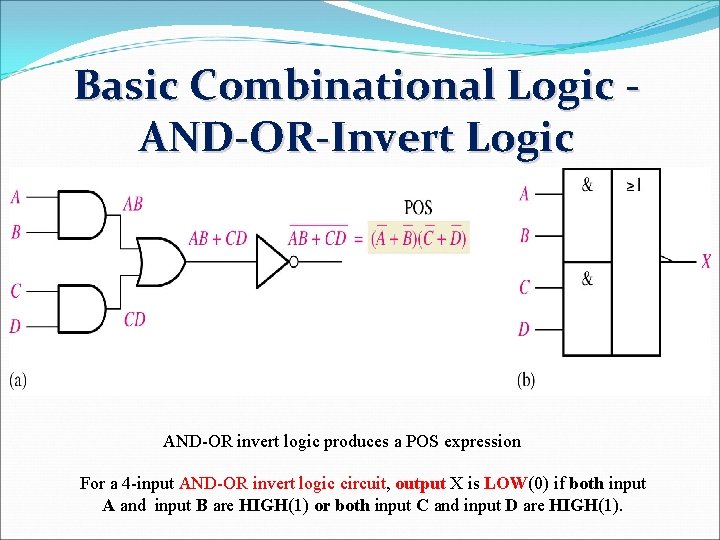
Basic Combinational Logic AND-OR-Invert Logic AND-OR invert logic produces a POS expression For a 4 -input AND-OR invert logic circuit, output X is LOW(0) if both input A and input B are HIGH(1) or both input C and input D are HIGH(1).

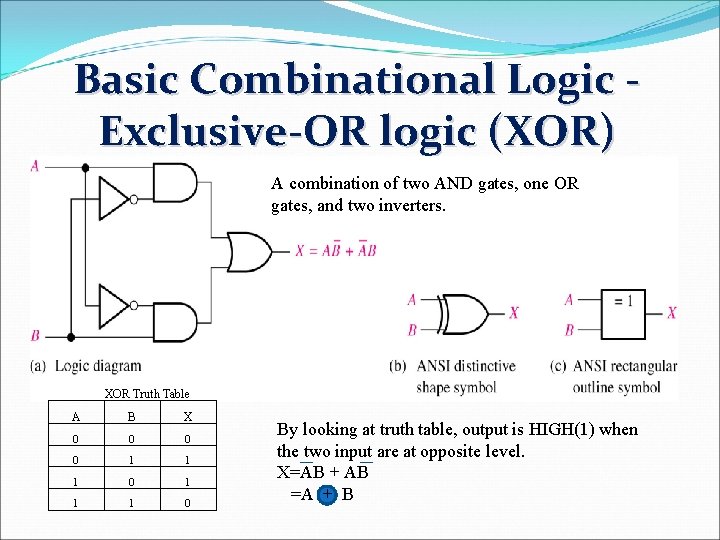
Basic Combinational Logic Exclusive-OR logic (XOR) A combination of two AND gates, one OR gates, and two inverters. XOR Truth Table A B X 0 0 1 1 1 0 By looking at truth table, output is HIGH(1) when the two input are at opposite level. X=AB + AB =A + B

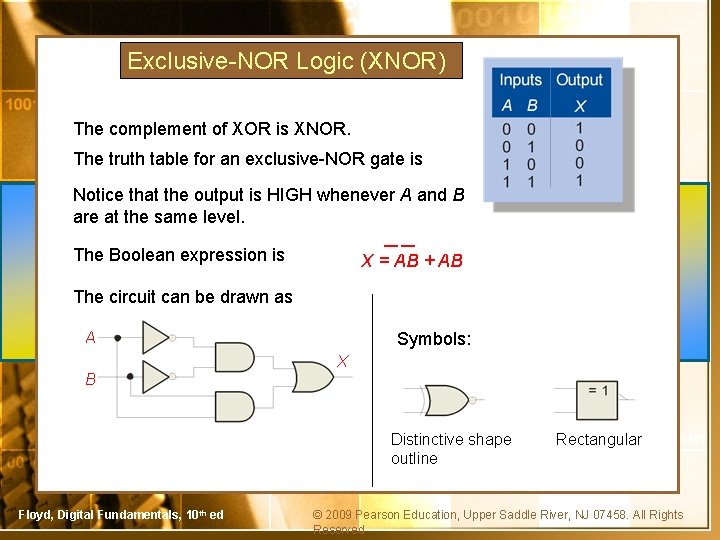
Exclusive-NOR Logic (XNOR) The complement of XOR is XNOR. The truth table for an exclusive-NOR gate is Notice that the output is HIGH whenever A and B are at the same level. The Boolean expression is X = AB + AB The circuit can be drawn as A Symbols: X B Distinctive shape outline Floyd, Digital Fundamentals, 10 th ed Rectangular © 2009 Pearson Education, Upper Saddle River, NJ 07458. All Rights Reserved

Complements(1) q Allow the representation of negative numbers q Complements are used in digital computers for simplifying the subtraction operation. q Two types of complement for binary numbers: § One’s complement § Two’s complement q The 1’s complement of a binary number is formed by changing 1’s to 0’s and 0’s to 1’s q Example: § The 1’s complement of 1011000 is 0100111 § The 1’s complement of 0101101 is 0101101 1010010

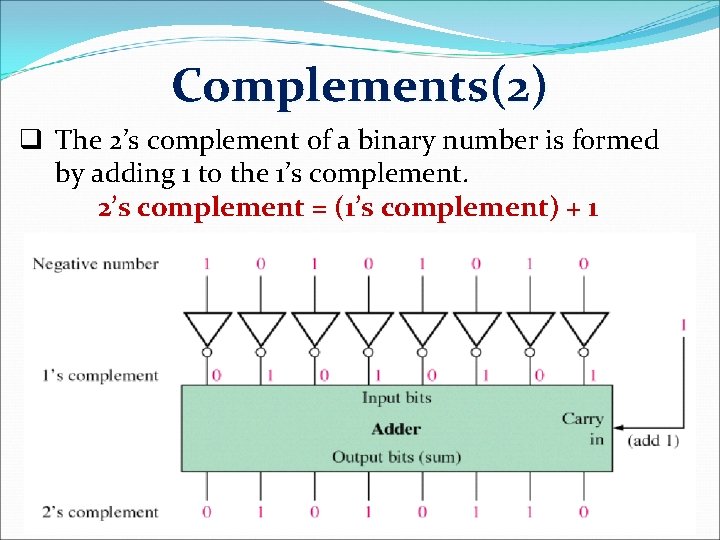
Complements(2) q The 2’s complement of a binary number is formed by adding 1 to the 1’s complement. 2’s complement = (1’s complement) + 1

Complements(3) q Alternative method to find 2’s complement: § Start at the right with the LSB and write the bits as they are up to including the first 1. § Do 1’s complements of the remaining bits. q Example: § The 2’s complement of 1101100 is 0010100 § The 2’s complement of 0110111 is 1001001

Binary Arithmetic Operations Subtraction q. Two binary numbers are subtracted by subtracting each pair of bits together with borrowing, where needed. q. Example: Example X: 229 Y: - 46 183 0 1 - 0 1 0 0 1 1 1 001 1 0 1 1 0 1 Borrow

Combinational Arithmetic Circuits q. Addition: q Half Adder (HA) q Full Adder (FA) q Carry Ripple Adders q. Subtraction: q Half Subtractor q Full Subtractor q Borrow Ripple Subtractors q Subtraction using adders

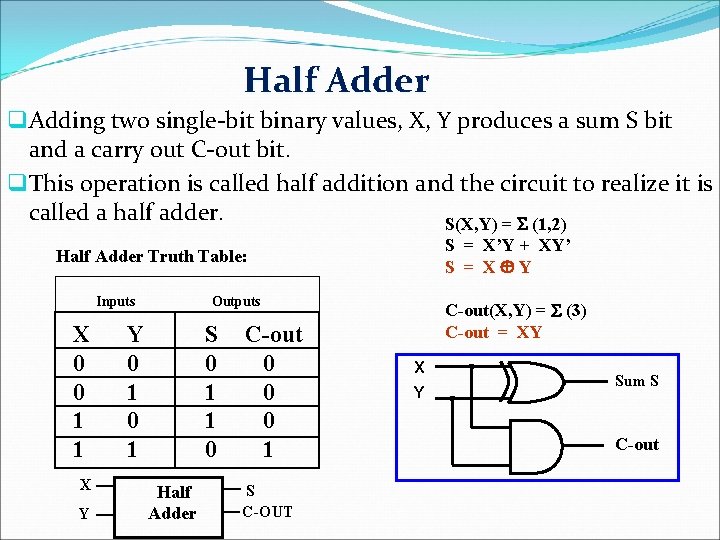
Half Adder q Adding two single-bit binary values, X, Y produces a sum S bit and a carry out C-out bit. q This operation is called half addition and the circuit to realize it is called a half adder. S(X, Y) = S (1, 2) S = X’Y + XY’ S = XÅY Half Adder Truth Table: Outputs Inputs X 0 0 1 1 X Y Y 0 1 S 0 1 1 0 Half Adder C-out 0 0 0 1 S C-OUT C-out(X, Y) = S (3) C-out = XY X Y Sum S C-out

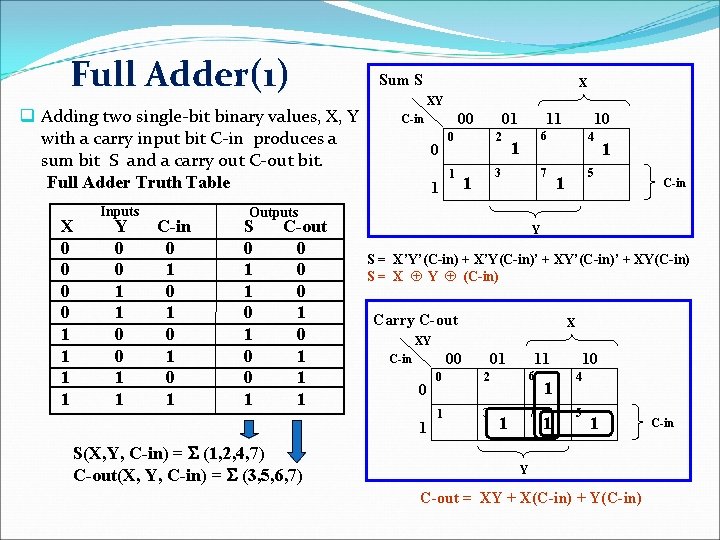
Full Adder(1) q Adding two single-bit binary values, X, Y with a carry input bit C-in produces a sum bit S and a carry out C-out bit. Full Adder Truth Table X 0 0 1 1 Inputs Y 0 0 1 1 C-in 0 1 0 1 Sum S X XY 00 C-in 0 1 01 0 1 2 11 6 1 3 1 10 7 4 1 5 1 C-in Outputs S 0 1 1 0 0 1 C-out 0 0 0 1 1 1 Y S = X’Y’(C-in) + X’Y(C-in)’ + XY’(C-in)’ + XY(C-in) S = X Å Y Å (C-in) Carry C-out XY 00 C-in 0 1 S(X, Y, C-in) = S (1, 2, 4, 7) C-out(X, Y, C-in) = S (3, 5, 6, 7) X 01 0 2 1 3 11 6 7 1 10 4 5 1 Y C-out = XY + X(C-in) + Y(C-in) C-in

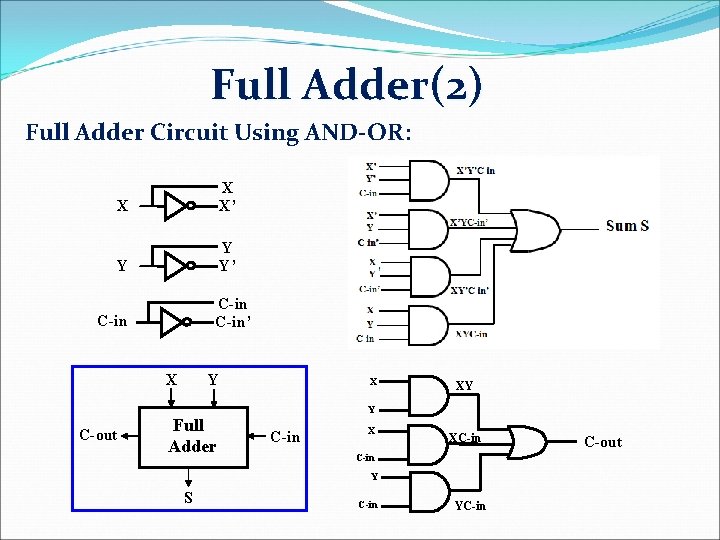
Full Adder(2) Full Adder Circuit Using AND-OR: X X X’ Y Y Y’ C-in’ C-in X C-out Y Full Adder X XY Y C-in X XC-in Y S C-in YC-in C-out

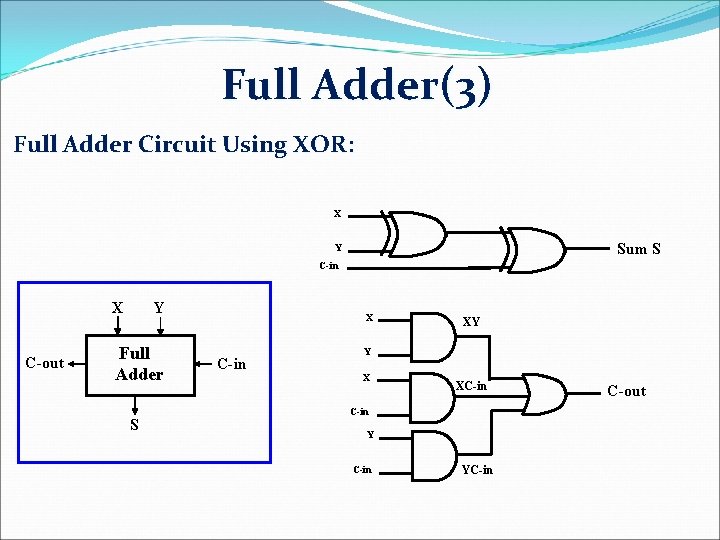
Full Adder(3) Full Adder Circuit Using XOR: X Sum S Y C-in X C-out Y Full Adder S X C-in XY Y X XC-in YC-in C-out

n-bit Carry Ripple Adders q An n-bit adder used to add two n-bit binary numbers can built by connecting in series n full adders. § Each full adder represents a bit position j (from 0 to n-1). § Each carry out C-out from a full adder at position j is connected to the carry in C-in of the full adder at the higher position j+1. q The output of a full adder at position j is given by: S j = Xj Å Yj Å Cj C j+1 = Xj. Yj + Xj. Cj + Y. Cj q In the expression of the sum Cj must be generated by the full adder at the lower position j-1. q The propagation delay in each full adder to produce the carry is equal to two gate delays = 2 D q Since the generation of the sum requires the propagation of the carry from the lowest position to the highest position , the total propagation delay of the adder is approximately: Total Propagation delay = 2 n. D

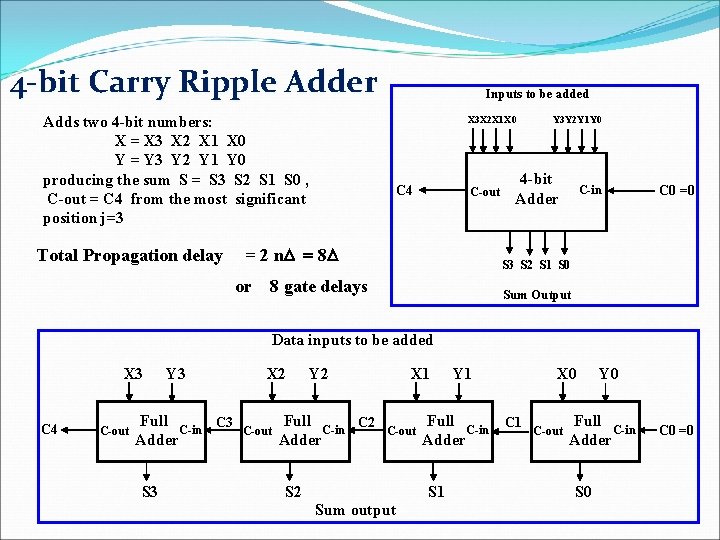
4 -bit Carry Ripple Adder Inputs to be added Adds two 4 -bit numbers: X = X 3 X 2 X 1 X 0 Y = Y 3 Y 2 Y 1 Y 0 producing the sum S = S 3 S 2 S 1 S 0 , C-out = C 4 from the most significant position j=3 Total Propagation delay X 3 X 2 X 1 X 0 C 4 C-out = 2 n. D = 8 D Y 3 Y 2 Y 1 Y 0 4 -bit Adder C-in C 0 =0 S 3 S 2 S 1 S 0 or 8 gate delays Sum Output Data inputs to be added X 3 C 4 C-out Y 3 Full C 3 C-in Adder S 3 X 2 C-out Y 2 Full C 2 C-in Adder X 1 C-out S 2 Full C-in Adder S 1 Sum output Y 1 X 0 C 1 C-out Y 0 Full C-in Adder S 0 C 0 =0

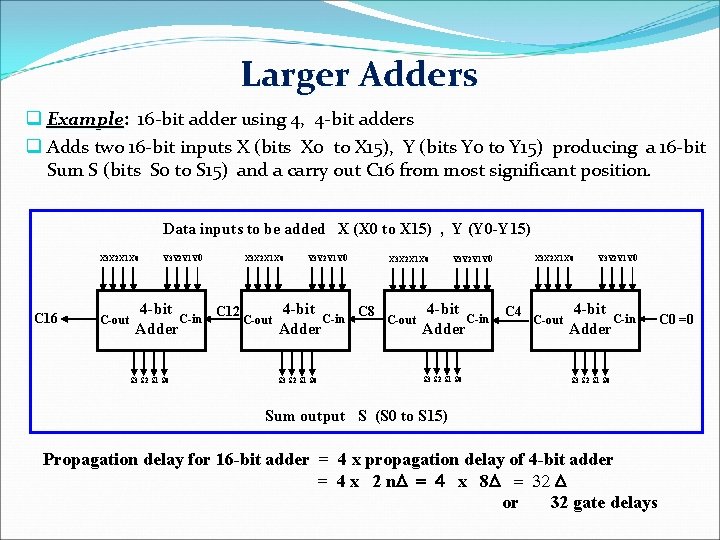
Larger Adders q Example: Example 16 -bit adder using 4, 4 -bit adders q Adds two 16 -bit inputs X (bits X 0 to X 15), Y (bits Y 0 to Y 15) producing a 16 -bit Sum S (bits S 0 to S 15) and a carry out C 16 from most significant position. Data inputs to be added X (X 0 to X 15) , Y (Y 0 -Y 15) X 3 X 2 X 1 X 0 C 16 C-out Y 3 Y 2 Y 1 Y 0 X 3 X 2 X 1 X 0 Y 3 Y 2 Y 1 Y 0 4 -bit C 12 C 8 C-in C-out Adder S 3 S 2 S 1 S 0 X 3 X 2 X 1 X 0 C-out Y 3 Y 2 Y 1 Y 0 4 -bit C-in Adder S 3 S 2 S 1 S 0 X 3 X 2 X 1 X 0 C 4 C-out Y 3 Y 2 Y 1 Y 0 4 -bit C-in Adder S 3 S 2 S 1 S 0 Sum output S (S 0 to S 15) Propagation delay for 16 -bit adder = 4 x propagation delay of 4 -bit adder = 4 x 2 n. D = 4 x 8 D = 32 D or 32 gate delays C 0 =0

Negative Binary Number Representations q Signed-Magnitude Representation: q For an n-bit binary number: Use the first bit (most significant bit, MSB) position to represent the sign where 0 is positive and 1 is negative. Ex: Sign 1 1 1 12 = - 12710 Magnitude q Remaining n-1 bits represent the magnitude which may range from: -2 (n-1) + 1 to 2(n-1) – 1 q This scheme has two representations for 0; i. e. , both positive and negative 0: for 8 bits: 0000, 10000000 q Arithmetic under this scheme uses the sign bit to indicate the nature of the operation and the sign of the result, but the sign bit is not used as part of the arithmetic.

Half Subtractor q Subtracting a single-bit binary value Y from anther X (I. e. X -Y ) produces a difference bit D and a borrow out bit B-out. q This operation is called half subtraction and the circuit to realize it is called a half subtractor. Half Subtractor Truth Table: Inputs X 0 0 1 1 Y 0 1 Outputs D(X, Y) = S (1, 2) D = X’Y + XY’ D = XÅY D B-out 0 0 1 1 1 0 0 0 B-out(X, Y) = S (1) B-out = X’Y X X Y Half Subtractor D B-OUT Y Difference D B-out

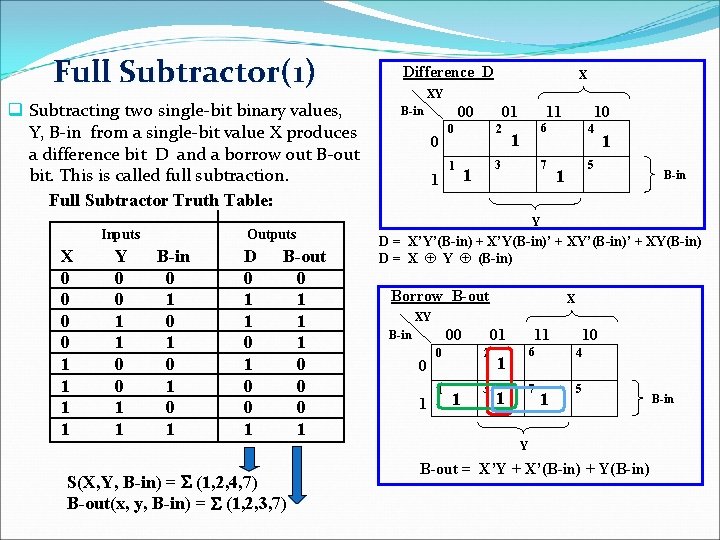
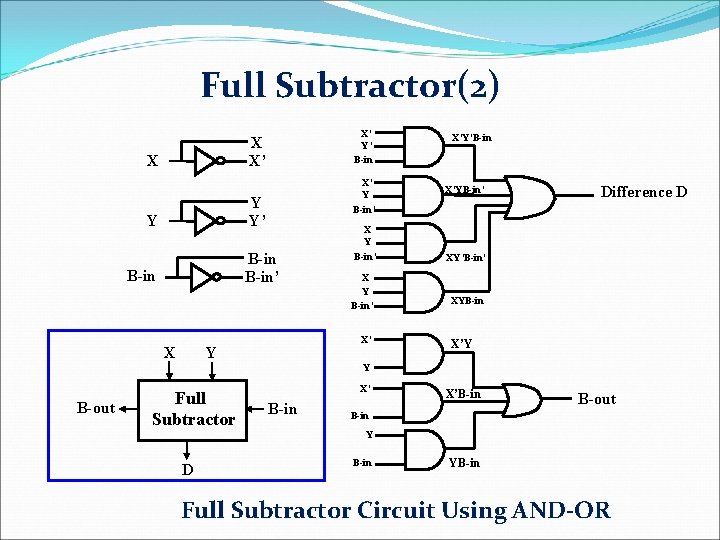
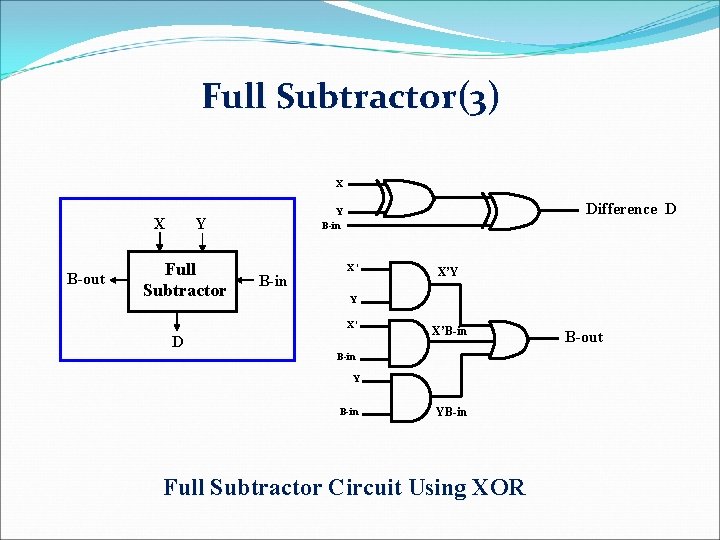
Full Subtractor(1) q Subtracting two single-bit binary values, Y, B-in from a single-bit value X produces a difference bit D and a borrow out B-out bit. This is called full subtraction. Full Subtractor Truth Table: Inputs X 0 0 1 1 Y 0 0 1 1 Outputs B-in 0 1 0 1 D 0 1 1 0 0 1 B-out 0 1 1 1 0 0 0 1 Difference D X XY 00 B-in 0 1 01 0 1 2 11 6 1 3 1 10 7 4 1 5 1 Y D = X’Y’(B-in) + X’Y(B-in)’ + XY’(B-in)’ + XY(B-in) D = X Å Y Å (B-in) Borrow B-out X XY 00 B-in 0 1 01 2 1 3 11 6 1 7 1 10 4 1 5 Y S(X, Y, B-in) = S (1, 2, 4, 7) B-out(x, y, B-in) = S (1, 2, 3, 7) B-in B-out = X’Y + X’(B-in) + Y(B-in) B-in

Full Subtractor(2) X’ Y’ B-in X X’ Y B-in’ Y Y’ Y X X’YB-in’ Difference D X Y B-in’ B-in X’Y’B-in’ X Y B-in’ X’ Y XY’B-in’ XYB-in X’Y Y B-out Full Subtractor X’ B-in X’B-in B-out B-in Y D B-in YB-in Full Subtractor Circuit Using AND-OR

Full Subtractor(3) X X B-out Y Full Subtractor Difference D Y B-in X’ X’Y Y X’ D X’B-in YB-in Full Subtractor Circuit Using XOR B-out

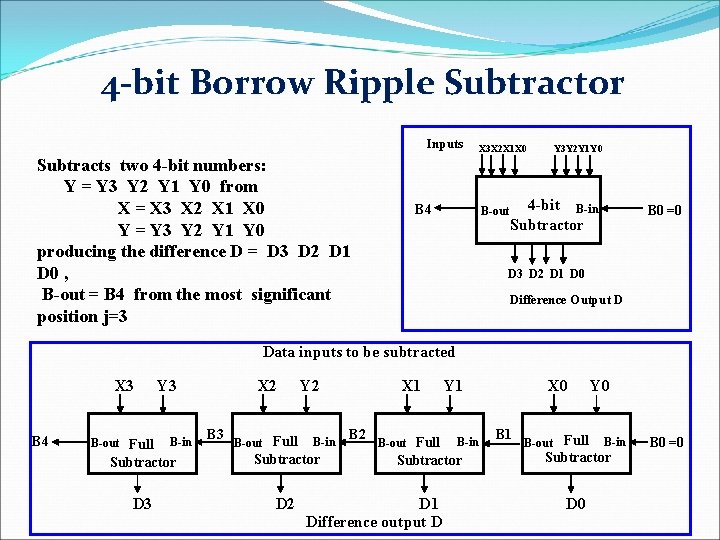
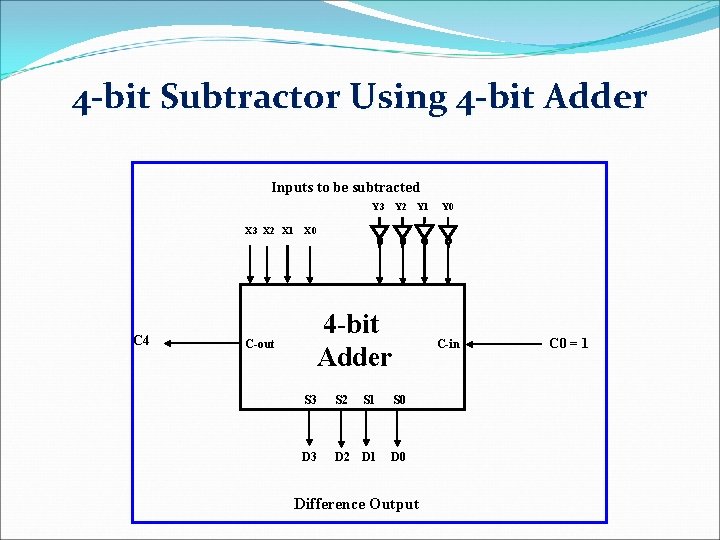
n-bit Subtractors An n-bit subtractor used to subtract an n-bit number Y from another n-bit number X (i. e X-Y) can be built in one of two ways: q By using n full subtractor and connecting them in series, creating a borrow ripple subtractor: § Each borrow out B-out from a full subtractor at position j is connected to the borrow in B-in of the full subtractor at the higher position j+1. q By using an n-bit adder and n inverters: § Find two’s complement of Y by: ü Inverting all the bits of Y using the n inverters. ü Adding 1 by setting the carry in of the least significant position to 1 § The original subtraction (X - Y) now becomes an addition of X to two’s complement of Y using the n-bit adder.

4 -bit Borrow Ripple Subtractor Inputs Subtracts two 4 -bit numbers: Y = Y 3 Y 2 Y 1 Y 0 from X = X 3 X 2 X 1 X 0 Y = Y 3 Y 2 Y 1 Y 0 producing the difference D = D 3 D 2 D 1 D 0 , B-out = B 4 from the most significant position j=3 X 3 X 2 X 1 X 0 B 4 B-out Y 3 Y 2 Y 1 Y 0 4 -bit B-in Subtractor B 0 =0 D 3 D 2 D 1 D 0 Difference Output D Data inputs to be subtracted X 3 B 4 B-out Full Y 3 B-in X 2 B 3 B-out Full Y 2 B-in Subtractor D 3 D 2 X 1 B 2 B-out Full Y 1 B-in Subtractor D 1 Difference output D X 0 B 1 B-out Full Y 0 B-in Subtractor D 0 B 0 =0

4 -bit Subtractor Using 4 -bit Adder Inputs to be subtracted Y 3 X 2 X 1 C 4 C-out Y 2 Y 1 Y 0 X 0 4 -bit Adder C-in S 3 S 2 S 1 S 0 D 3 D 2 D 1 D 0 Difference Output C 0 = 1

Examples: q Add the two 4 -bit binary numbers A = 1101 and B = 0111. Then show that the parallel binary adder adds the two numbers correctly. q Use 2’s compliment addition to subtract 12 from 25. Then draw subtraction process by using a binary adder. q Determine the binary output for the parallel binary adder for the inputs shown. 1 C 4 C-out 0 Full C 3 C-in Adder S 3 1 C-out 1 Full C 2 C-in Adder 0 C-out S 2 1 Full C-in Adder S 1 Sum output 1 C-out 1 Full C-in Adder S 0 C 0 = gnd

Next lecture…. q Converters ~ Comparator ~ Decoder ~ Encoder ~ Code converter