Eksamen 2005 oppgave 2 Eksamen 2006 oppgave 2






- Slides: 13

Eksamen 2005, oppgave 2 Eksamen 2006, oppgave 2 Stein Krogdahl INF 5110 – V 2007

Oppgave 2 a og 2 b, 2005 Betrakt følgende grammatikk G 1: E → S E | num S→-S|+S|ε hvor E og S er ikke-terminalsymboler, E er startsymbol og: +, -, num er terminalsymboler (med vanlig tolkning). Oppgave 2 a: Beskriv kort hvordan setninger som G 1 kan produsere ser ut, og gi ett eksempel på en setning med 4 terminalsymboler. Svar: Setningene som produseres et tall med et vilkårlig antall fortegn (+ eller -) foran, f. eks: +--5 Oppgave 2 b: Gi et regulært uttrykk som lager de samme setningene som G 1. Svar: (+|-)* num

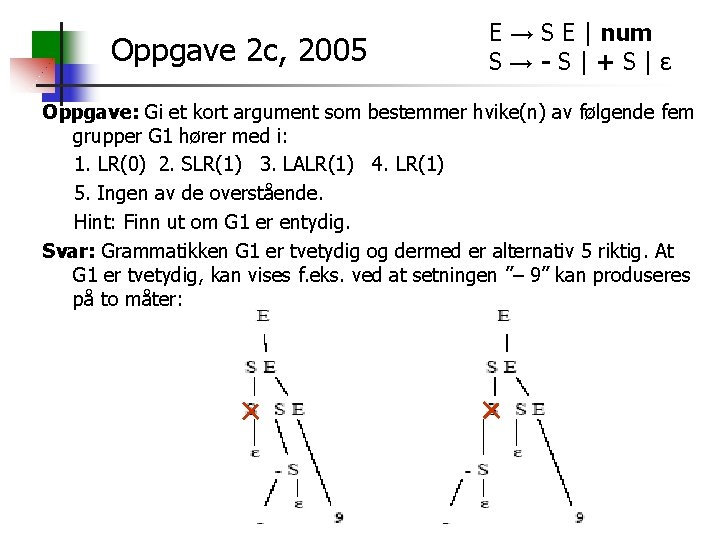
Oppgave 2 c, 2005 E → S E | num S→-S|+S|ε Oppgave: Gi et kort argument som bestemmer hvike(n) av følgende fem grupper G 1 hører med i: 1. LR(0) 2. SLR(1) 3. LALR(1) 4. LR(1) 5. Ingen av de overstående. Hint: Finn ut om G 1 er entydig. Svar: Grammatikken G 1 er tvetydig og dermed er alternativ 5 riktig. At G 1 er tvetydig, kan vises f. eks. ved at setningen ”– 9” kan produseres på to måter:

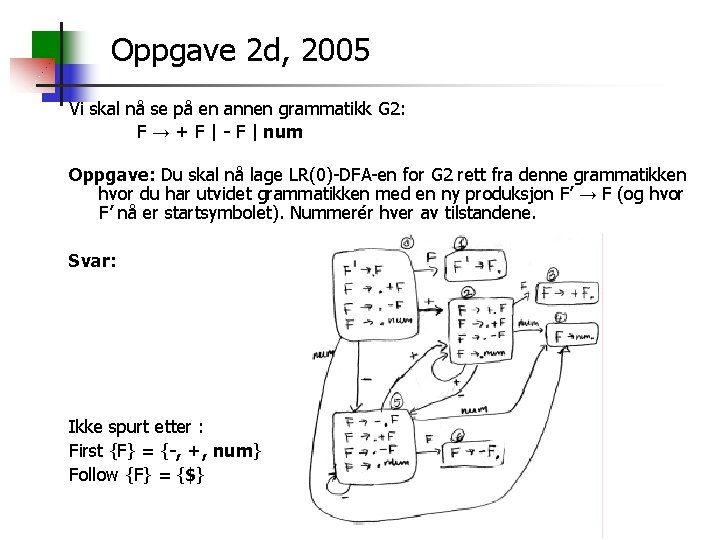
Oppgave 2 d, 2005 Vi skal nå se på en annen grammatikk G 2: F → + F | - F | num Oppgave: Du skal nå lage LR(0)-DFA-en for G 2 rett fra denne grammatikken hvor du har utvidet grammatikken med en ny produksjon F’ → F (og hvor F’ nå er startsymbolet). Nummerér hver av tilstandene. Svar: Ikke spurt etter : First {F} = {-, +, num} Follow {F} = {$}

Oppgave 2 e, 2005 F → + F | - F | num Oppgave: Ut fra det svaret på d), angi med en kort begrunnelse hvilke(n) type grammatikk G 2 er (jfr. spørsmål 2 c ovenfor). Svar: First {F} = {-, +, num} Follow {F} = {$} (men vi får ikke bruk for dette) Vi har ingen konflikter (shift/shift eller shift/reduce) i LR(0)DFA’en og grammatikken er følgelig LR(0).

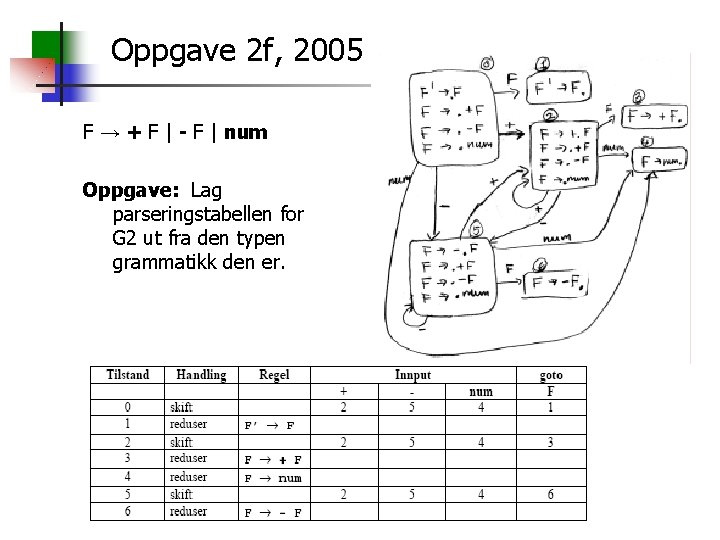
Oppgave 2 f, 2005 F → + F | - F | num Oppgave: Lag parseringstabellen for G 2 ut fra den typen grammatikk den er.

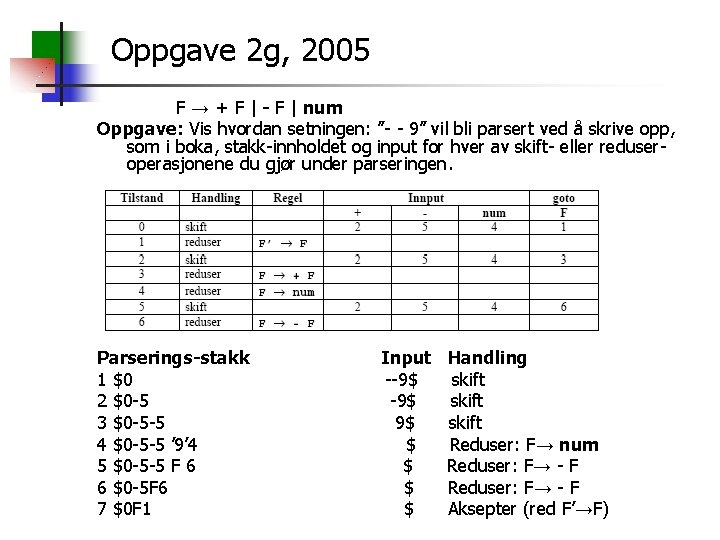
Oppgave 2 g, 2005 F → + F | - F | num Oppgave: Vis hvordan setningen: ”- - 9” vil bli parsert ved å skrive opp, som i boka, stakk-innholdet og input for hver av skift- eller reduseroperasjonene du gjør under parseringen. Parserings-stakk 1 $0 2 $0 -5 3 $0 -5 -5 4 $0 -5 -5 ’ 9’ 4 5 $0 -5 -5 F 6 6 $0 -5 F 6 7 $0 F 1 Input --9$ 9$ $ $ Handling skift Reduser: F→ num Reduser: F→ - F Aksepter (red F’→F)

Oppgave 2 a, 2006 S→T S S→T T→# T T→a Oppgave: Finn First og Follow-mengdene til T og S (og la $ betegne ’end-of-file’ som i boka). S T First a# a# Follow $ a#$

Oppgave 2 b og 2 c, 2006 S→T S S→T T→# T T→a Oppgave 2 b: Formulér med dine egne ord hvilke sekvenser av terminalsymboler du kan lage ut fra S’. Svar: Vi kan fra S generere en-eller-flere ’a’-er hvor hver a har null eller flere # foran seg. Oppgave 2 c: Avgjør om du kan lage et regulært uttrykk som uttrykker disse sekvensene av # og a som du kan utlede fra S, og hvis svaret er ’ja’, gi et slikt regulært uttrykk. Svar: Vi har flg. regulære uttrykk { {#}* a}+

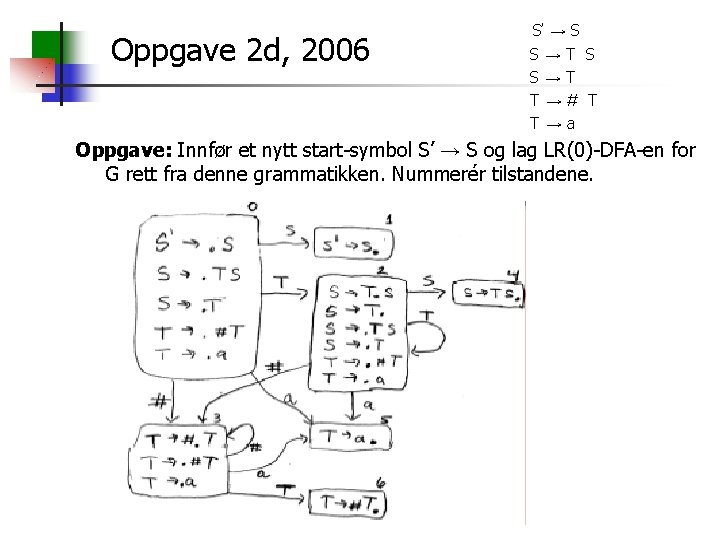
Oppgave 2 d, 2006 S’ → S S→T T→# T T→a Oppgave: Innfør et nytt start-symbol S’ → S og lag LR(0)-DFA-en for G rett fra denne grammatikken. Nummerér tilstandene.

Oppgave 2 e, 2006 Oppgave: Gi et kort argument som bestemmer hvike(n) av følgende fem grupper G hører med i: a. LR(1) b. LALR(1) c. SLR(1) d. LR(0) e. Ingen av de overstående. Svar: n Den er ikke LR(0) fordi det er en shift/red-konflikt i tilstand 2. n Den er SLR(1) fordi skift/reduser-konflikten vi har i tilstand 2 kan løses ved at: Follow-mengden til S ikke inneholder # eller a Altså i tilstand 2: n n n Har vi $ (er eneste symbol i Follow (S) ) gjør vi reduksjonen S -> T Ellers gjør vi en skift Siden er SLR(1), er den også LALR(1) og LR(1). Den er følgelig også entydig.

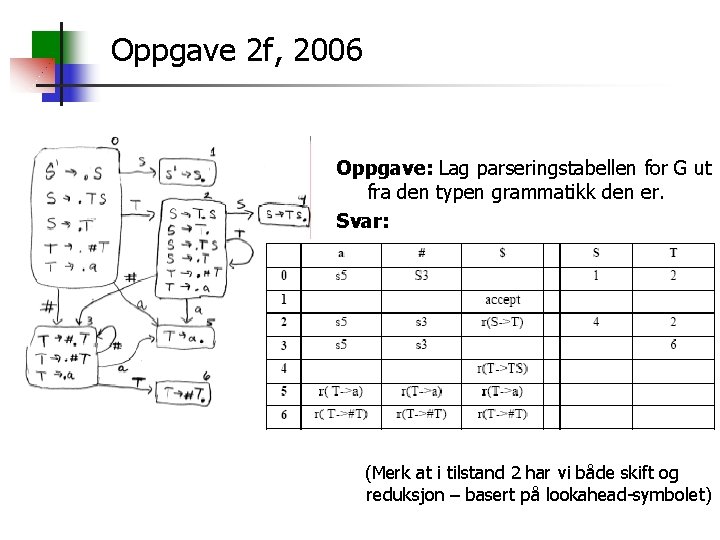
Oppgave 2 f, 2006 Oppgave: Lag parseringstabellen for G ut fra den typen grammatikk den er. Svar: (Merk at i tilstand 2 har vi både skift og reduksjon – basert på lookahead-symbolet)

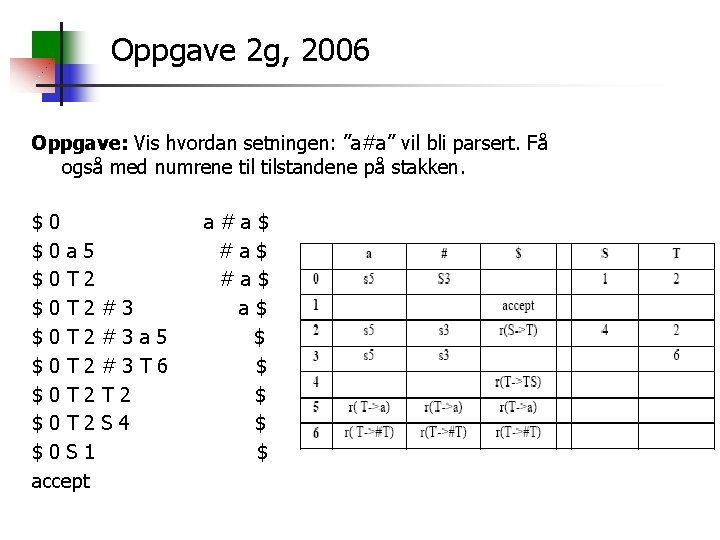
Oppgave 2 g, 2006 Oppgave: Vis hvordan setningen: ”a#a” vil bli parsert. Få også med numrene tilstandene på stakken. $0 $0 a 5 $0 T 2 $0 T 2 $0 S 1 accept #3 #3 a 5 #3 T 6 T 2 S 4 a#a$ #a$ a$ $ $
 (2005-2006) school calendar
(2005-2006) school calendar Diagnostiske oppgaver
Diagnostiske oppgaver Cytoplasma oppgave
Cytoplasma oppgave Eksempel på avslutning i oppgave
Eksempel på avslutning i oppgave Hvordan skrive en juridisk oppgave
Hvordan skrive en juridisk oppgave Postakut abstinens benzo
Postakut abstinens benzo Acto legislativo de 2005
Acto legislativo de 2005 En madrid a 19 de abril de 2005
En madrid a 19 de abril de 2005 Server management studio express
Server management studio express Magazioner despartit in silabe
Magazioner despartit in silabe Permenkes no 168 tahun 2005 mengatur tentang
Permenkes no 168 tahun 2005 mengatur tentang Pp nomor 23 tahun 2005
Pp nomor 23 tahun 2005 Rr 11-2005
Rr 11-2005 Pearson education limited 2005
Pearson education limited 2005

























