Einsteins Theory of Relativity 5 Accelerated CS in

Einstein‘s Theory of Relativity 5. Accelerated CS in Special Relativity, Equivalence Principle, Motion in a Gravitational Field, Geodesic Equation Ulrich R. M. E. Geppert 3/7/2021 U. R. M. E. Zielona Gora 1

coefficients of metric tensor are generally functions of coordinates e. g. polar or cylindrical coordinates y x coordinate transformation cartesian ⇾ polar (or cylindrical) Dependenc of the metric tensor on coordinates may be caused by the use of curvilinear coordinates. 3/7/2021 U. R. M. E. Zielona Gora 2

special relativistic laws hold only in inertial systems other coordinate systems are allowed too, there appear, however, additional terms Newton‘s 2 nd axiom: pseudo force: centrifugal Pseudo forces feels the observer co-rotating with CS‘, the observer in IS doesn‘t see them. 3/7/2021 U. R. M. E. Zielona Gora 3

coordinate transformation: (see Annex) metric tensor becomes dependent on coordinates a feature of GR 3/7/2021 U. R. M. E. Zielona Gora 4

3/7/2021 U. R. M. E. Zielona Gora 5

This form we will meet in the course of our lectures very often! 3/7/2021 U. R. M. E. Zielona Gora 6

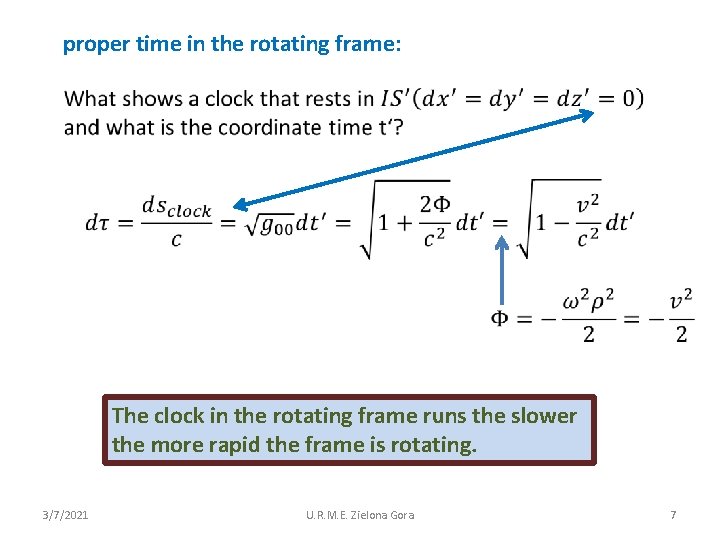
proper time in the rotating frame: The clock in the rotating frame runs the slower the more rapid the frame is rotating. 3/7/2021 U. R. M. E. Zielona Gora 7

i. e. equ. of 4 -D spherical surface, flash propagates like an expanding surface of a sphere - A sends light signal to B A B - B reflects signal to A 3/7/2021 U. R. M. E. Zielona Gora 8

3/7/2021 U. R. M. E. Zielona Gora 9

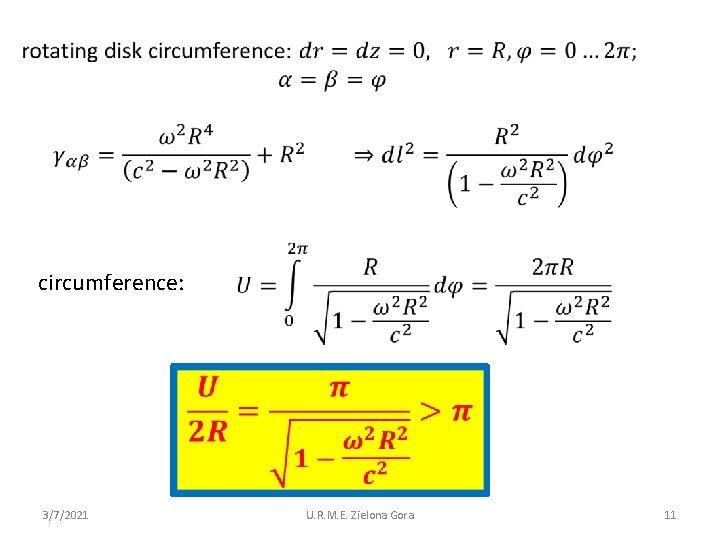
reminder: path element in cylindrical coordinates: transformation into a rotating system: 3/7/2021 U. R. M. E. Zielona Gora 10

circumference: 3/7/2021 U. R. M. E. Zielona Gora 11

„Ehrenfest-paradox“: radius remains constant but circumference is stretched or shrinked (depending on the state of the observer) surface of the disk is either concave ore convex from the point of view of the observer there is no Euklidean geometry in the rotating system ⇒ another geometry is necessary Georg Friedrich Bernhard Riemann (1826 -1866) geometry of curved spaces 3/7/2021 U. R. M. E. Zielona Gora 12

classical motion of a point mass in accelerated CS under influence of gravity: pseudo forces, depend on geometry suggesting: why is gravitation not a property of space? ⇒ geometrization of gravitation 3/7/2021 U. R. M. E. Zielona Gora 13

Equivalence Principle lift experiments The lift is placed in a rocket ship in a part of the universe far removed from gravitating bodies. The rocket is accelerated forward with a constant acceleration g relative to an inertial observer. The observer releases a body from rest and sees it fall to the floor with acceleration g. The rocket motor is switched off so that the lift undergoes uniform motion relative to the inertial observer. A released body is found to remain at rest relative to the observer in the lift. 3/7/2021 U. R. M. E. Zielona Gora 14

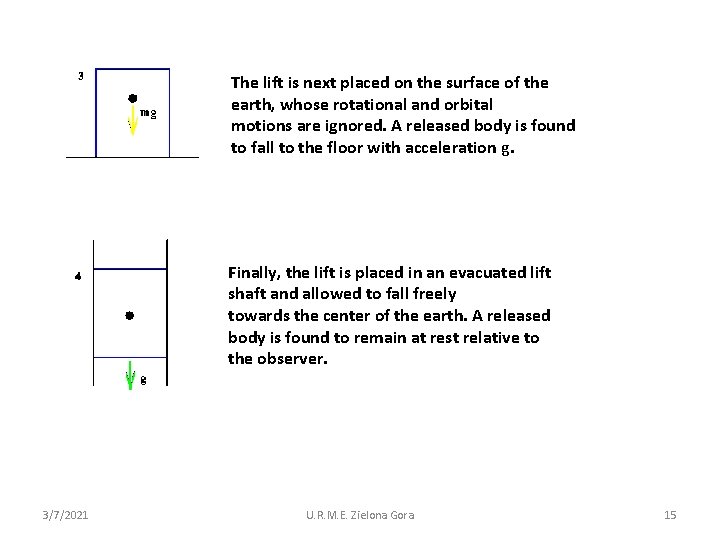
The lift is next placed on the surface of the earth, whose rotational and orbital motions are ignored. A released body is found to fall to the floor with acceleration g. Finally, the lift is placed in an evacuated lift shaft and allowed to fall freely towards the center of the earth. A released body is found to remain at rest relative to the observer. 3/7/2021 U. R. M. E. Zielona Gora 15

conclusions: 1. gravitational and inertial mass are equal 2. gravitational and inertial forces are equivalent 3. in Local Inertial Systems (LIS, lab in satellite, lift), the laws of SR are valid without gravitation Inertial and gravitational forces a free falling CS is a LIS; it is not an IS because it is accelerated are locally indistinguishable! e. g. wrt the fixed stars in a free falling CS all processes proceed as though exists no gravitation equivalence principle: In a Local Inertial System the laws of SR are valid! 3/7/2021 U. R. M. E. Zielona Gora 16

equivalence principle allows to derive relativistic laws with gravitation SR law without gravitation coordinatetransf. relativistic law with gravitation coordinate transformation: contains the relative acceleration between LIS and global CS relative acceleration corresponds to the gravitational field 3/7/2021 U. R. M. E. Zielona Gora 17

3/7/2021 U. R. M. E. Zielona Gora 18

mathematical meaning of the equivalence principle: space-time with gravitation is locally a Minkowski one 3/7/2021 U. R. M. E. Zielona Gora 19

Motion in a Gravitational Field equivalence principle: in a LIS (satellite, free falling lift) the laws of SR are valid motion of a force free mass point 3/7/2021 U. R. M. E. Zielona Gora 20

3/7/2021 U. R. M. E. Zielona Gora 21

3/7/2021 U. R. M. E. Zielona Gora 22

⇒ the global metric tensor is: in GR are all such forces equivalent 3/7/2021 U. R. M. E. Zielona Gora 23

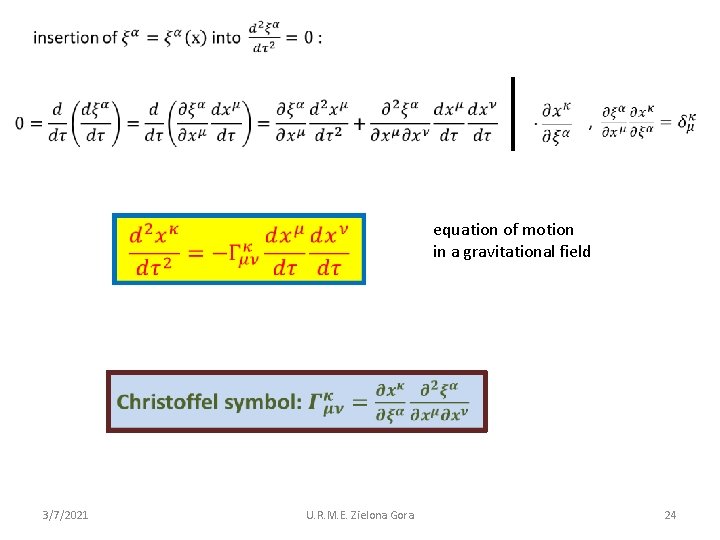
equation of motion in a gravitational field 3/7/2021 U. R. M. E. Zielona Gora 24

- gravitational forces describe coupling between gravitational field an matter - equ. of motion has been derived from equivalence principle - equivalence principle determines coupling between gravitational field and matter 3/7/2021 U. R. M. E. Zielona Gora 25

according to equivalence principle: photon (light) moves in LIS on straight lines 3/7/2021 U. R. M. E. Zielona Gora 26

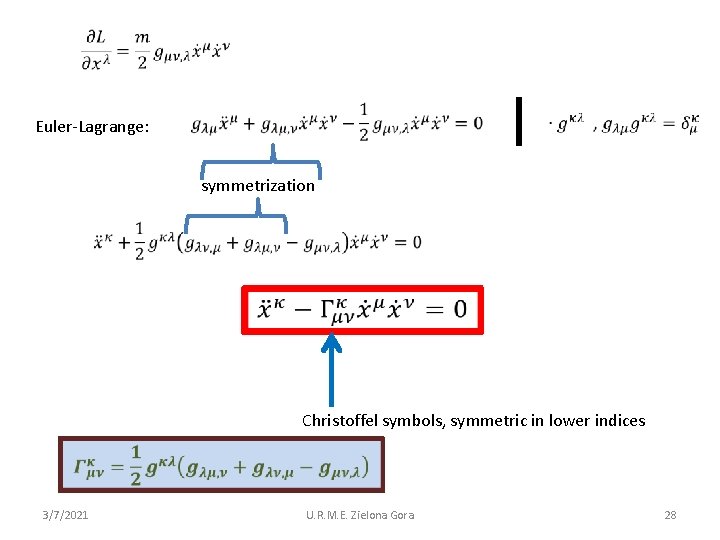
alternatively: derivation of the equ. of motion by use of Euler-Lagrange: static gravitational field partial derivative 3/7/2021 U. R. M. E. Zielona Gora 27

Euler-Lagrange: symmetrization Christoffel symbols, symmetric in lower indices 3/7/2021 U. R. M. E. Zielona Gora 28

(see annex, if you want) read off from equ. of motion we have two expressions for the Christoffel symbol: and 3/7/2021 do they coincide? U. R. M. E. Zielona Gora 29

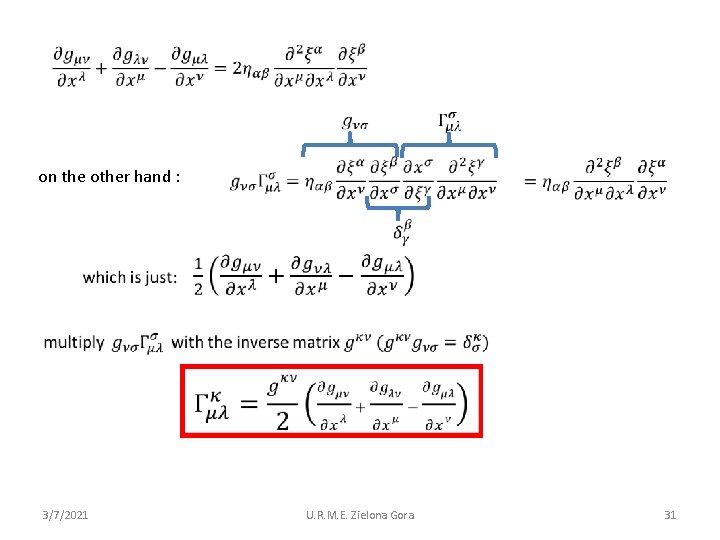
comparison of and consider combination of first derivatives: 3/7/2021 U. R. M. E. Zielona Gora 30

on the other hand : 3/7/2021 U. R. M. E. Zielona Gora 31

reminder to GR 3: equ. of motion of a particle in an elm. field: 3/7/2021 U. R. M. E. Zielona Gora 32

a useful conclusion: It is often easier to calculate the Christoffel symbols from Lagrange II than by evaluating 3/7/2021 U. R. M. E. Zielona Gora 33

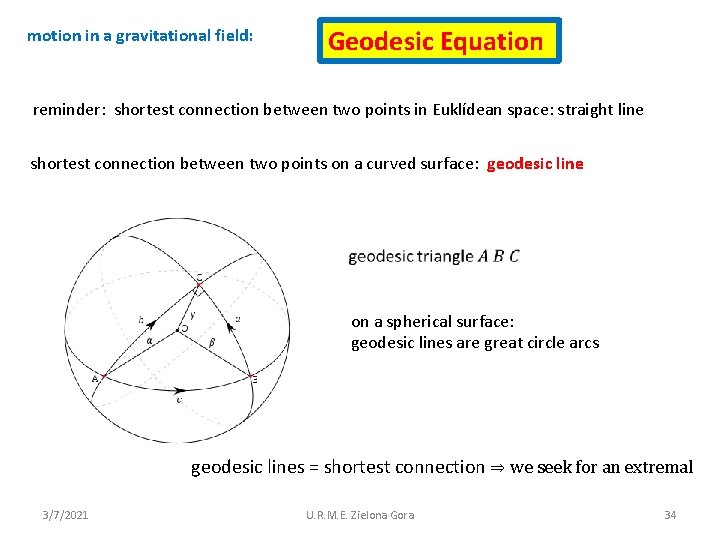
motion in a gravitational field: Geodesic Equation reminder: shortest connection between two points in Euklídean space: straight line shortest connection between two points on a curved surface: geodesic line on a spherical surface: geodesic lines are great circle arcs geodesic lines = shortest connection ⇒ we seek for an extremal 3/7/2021 U. R. M. E. Zielona Gora 34

find that curve between 2 points for which the arc length is minimum parametrization Hamilton‘s principle: action is an extremum ⇒ Euler- Lagrange equation 3/7/2021 U. R. M. E. Zielona Gora 35

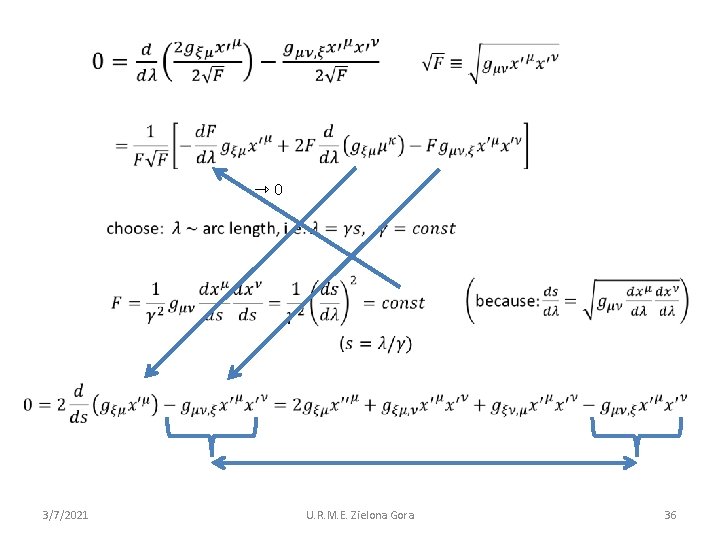
⇾ 0 3/7/2021 U. R. M. E. Zielona Gora 36

solutions of this equations: geodesic lines geodesic equation: 3/7/2021 U. R. M. E. Zielona Gora 37

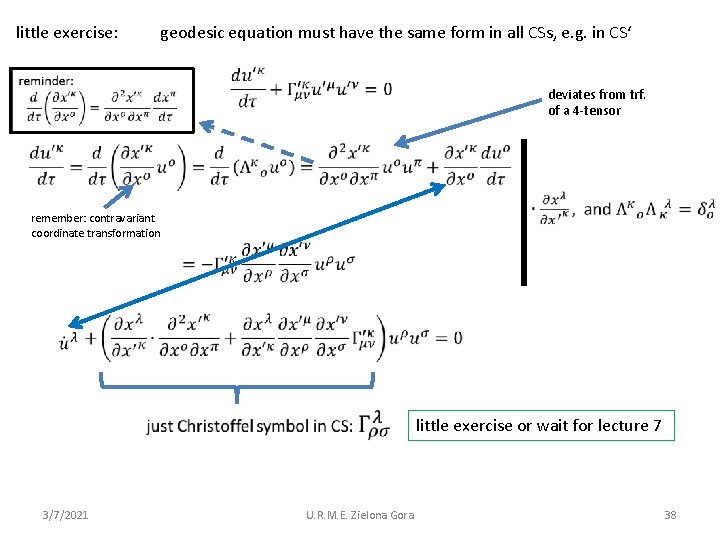
little exercise: geodesic equation must have the same form in all CSs, e. g. in CS‘ deviates from trf. of a 4 -tensor remember: contravariant coordinate transformation 3/7/2021 little exercise or wait for lecture 7 U. R. M. E. Zielona Gora 38

Christoffel symbol is not a 4 -tensor For each point P in a curved space-time one can find always a coordinate system, in which the metric is a Minkowski one and all Christoffel symbols disappear. I. e. it can always be found a locally flat (locally geodesic) coordinate system. proof : 3/7/2021 U. R. M. E. Zielona Gora 39

partial derivative of metric tensor: + 3/7/2021 U. R. M. E. Zielona Gora 40

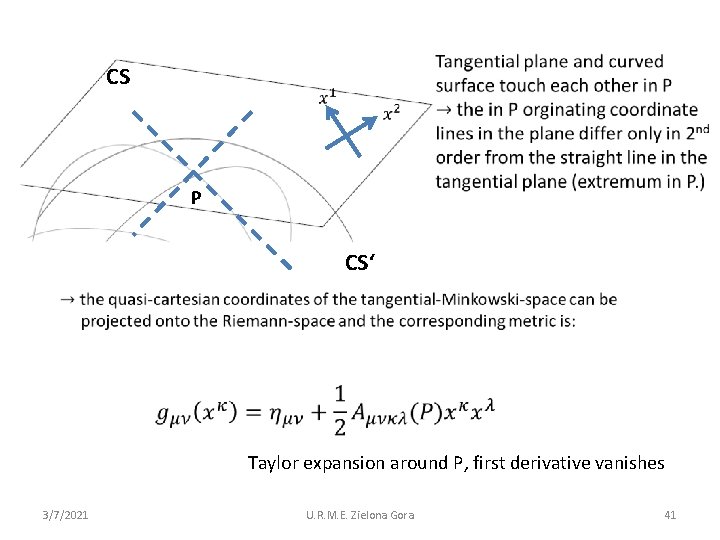
CS P CS‘ Taylor expansion around P, first derivative vanishes 3/7/2021 U. R. M. E. Zielona Gora 41

3/7/2021 U. R. M. E. Zielona Gora 42

3/7/2021 U. R. M. E. Zielona Gora 43

In the geodesic equation is the gravitation via the metric tensor hidden in the Christoffel symbol. 3/7/2021 U. R. M. E. Zielona Gora 44

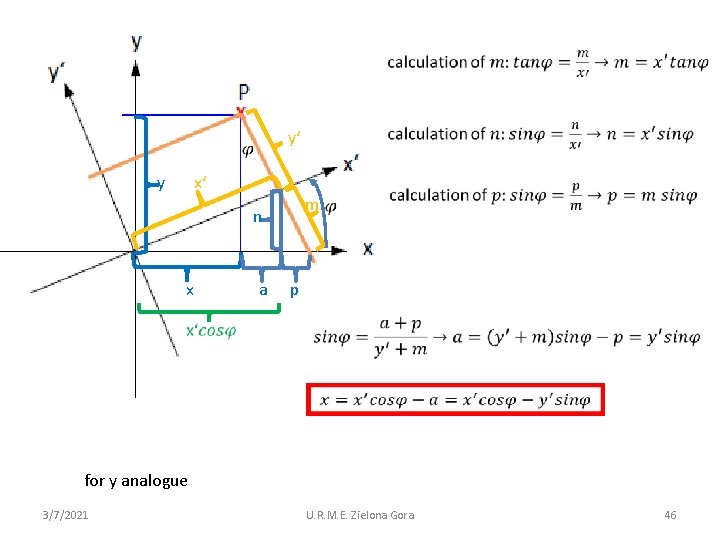
Annex: derivation of the rotational matrix 3/7/2021 U. R. M. E. Zielona Gora 45

y x‘ m n x y‘ a p for y analogue 3/7/2021 U. R. M. E. Zielona Gora 46

Annex: velocity in spherical coordinates unit vectors: tangent vectors to the respective coordinate in direction of growing coordinate 3/7/2021 U. R. M. E. Zielona Gora 47

3/7/2021 U. R. M. E. Zielona Gora 48

proof: 3/7/2021 U. R. M. E. Zielona Gora 49