Einsteins Theory of Relativity 0 Introduction Ulrich R

Einstein‘s Theory of Relativity 0. Introduction Ulrich R. M. E. Geppert 11/1/2020 U. R. M. E. Zielona Gora 1

Relativity in everydays life: GPS – Navigation - 24 satellites, altitude ~ 20000 km, orbital speed 14000 km/h - determines the absolute position on Earth surface within ~ 5 m - ⇒ clock ticks must be known with accuracy of 20… 30 ns Special relativity: satellites in motion relative to Earth surface: - on-board clocks are slower than clocks on Earth ⇒ satellite atomic clocks fall behind 7 μs/day General relativity: satellites high above the Earth: - Curvature of spacetime less than on Earth‘s surface - Earth‘s clocks tick more slowly than satellite‘s clocks ⇒ GPS satellite clock get ahead of ground-based clocks by 45 μs/day 11/1/2020 U. R. M. E. Zielona Gora 2

SR time diletation: GR time diletation: 11/1/2020 U. R. M. E. Zielona Gora 3

Combination of these two relativistic effects: On-board clocks tick faster than identical clocks on ground by 38 μs/day ≫ 38 ns/day ⇒ not sufficient accuracy How large is the deviation? If relativistic effects are not properly taken into account, errors in global positions would accumulate at a rate of 10 km/day!!! 11/1/2020 U. R. M. E. Zielona Gora 3

Two important terms: Proper time/proper length ⇔ coordinate time/length of the observer, both in SR and GR Curvature of space-time 11/1/2020 only in GR U. R. M. E. Zielona Gora 4

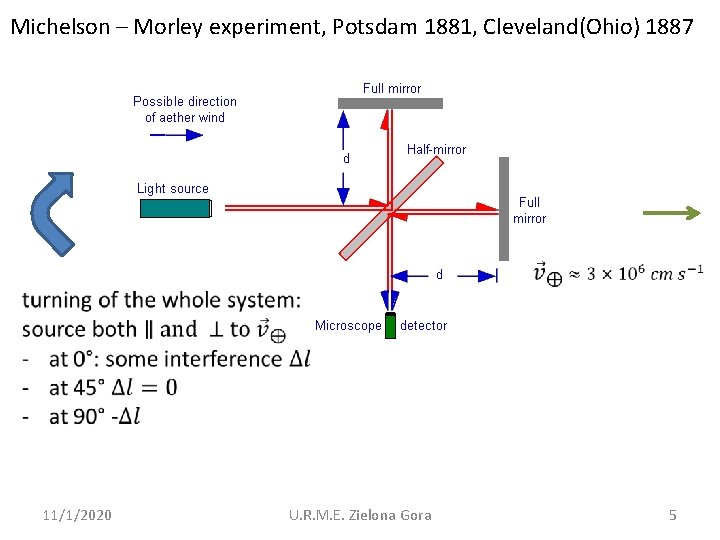
Michelson – Morley experiment, Potsdam 1881, Cleveland(Ohio) 1887 11/1/2020 U. R. M. E. Zielona Gora 5

Assumption: Gallilei-transformation is correct! x X‘ 11/1/2020 U. R. M. E. Zielona Gora 6

This shift has not been seen!!! 11/1/2020 U. R. M. E. Zielona Gora 7

Are the laws of physics invariant under Galilei transformation? Newton‘s equation of motion: Equ. of motion is valid also in the IS‘ which moves with constant v relative to IS ⇒ invariant (covariant). Maxwell‘s wave equation: 1 11/1/2020 0 U. R. M. E. Zielona Gora 8

1 Maxwell equations not invariant under Galilei transformation! not forminvariant 11/1/2020 U. R. M. E. Zielona Gora 9

Somthing must be wrong with the Galilei-transformation. - light is not like sound, with a definite speed relative to some underlying medium - light is also not like bullets, with a definite speed relative to the source of the light. Electromagnetic waves propagate in vacuum in each inertial system isotropical with the velocity of light. 11/1/2020 U. R. M. E. Zielona Gora 10

Which transformation returns the correct result? obviously wrong! Lorentz transformation 11/1/2020 U. R. M. E. Zielona Gora 11

Lorentz transformation Galilei: space (x, y, z) and time (t) absolut, independent on each other Einstein: the laws of physics have the same form in each inertial system Synonymous: The laws of physics are invariant under Lorentz transformations. space and time spacetime x, y, z; t x, y, z, ct 11/1/2020 U. R. M. E. Zielona Gora 12

Einstein‘s principle of relativity: the laws of physics (Newtons eqs. of motion, Maxwell-eqs. , …. ) are valid in all IS, i. e. they are forminvariant (covariant) under the transformation between IS and IS‘ (that moves with velocity v 0=v(t, t measured in IS) with respect to IS). The transformation that lets the laws forminvariant is the Lorentz transformation. 11/1/2020 U. R. M. E. Zielona Gora 13

expansion of a light wave in an IS: realization of spacetime coordinate How can in each space point the time be realized? Equation of a 4 -D Lightflash propagates like an expanding spherical surface of a sphere. Invariant under LT 11/1/2020 U. R. M. E. Zielona Gora 14

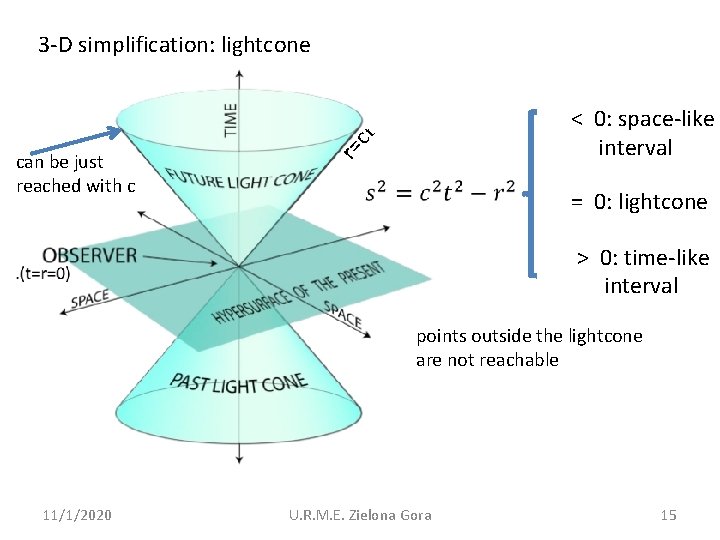
3 -D simplification: lightcone can be just reached with c r= ct < 0: space-like interval = 0: lightcone > 0: time-like interval points outside the lightcone are not reachable 11/1/2020 U. R. M. E. Zielona Gora 15

On the lightcone are located all spacetime points, from which „ 0“ can be reached with c. - between all points inside the lightcone exist causality, propagation of action is possible, timelike intervals are real - between all points outside the lightcone exist no causality, propagation of action is impossible, spacelike intervals are imaginary 11/1/2020 U. R. M. E. Zielona Gora 16

If all IS are equivalent: The intervall of spacetime has to be invariant under transformation from IS ⇒IS‘: - homogeneity of space: transformation has to be linear - IS‘ moves with v wrt IS along the x-axis, y‘=y, z‘=z 11/1/2020 U. R. M. E. Zielona Gora 17

11/1/2020 U. R. M. E. Zielona Gora 18

11/1/2020 U. R. M. E. Zielona Gora 19

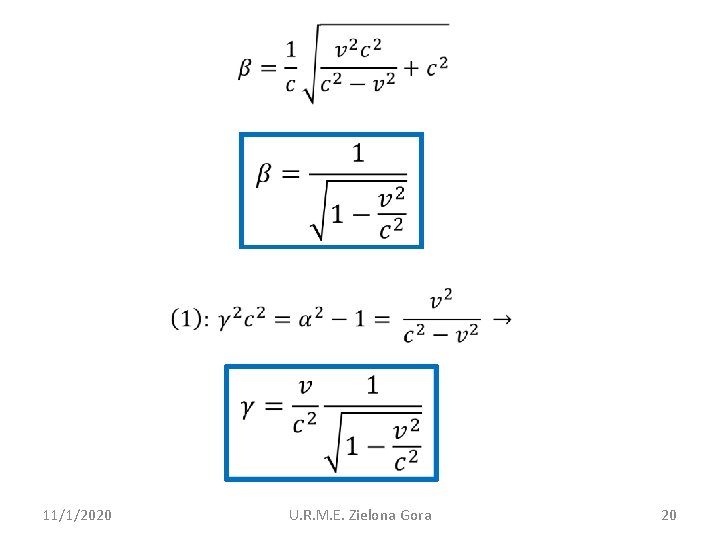
11/1/2020 U. R. M. E. Zielona Gora 20

defined only for v<c Correlation between space and time 11/1/2020 U. R. M. E. Zielona Gora 21

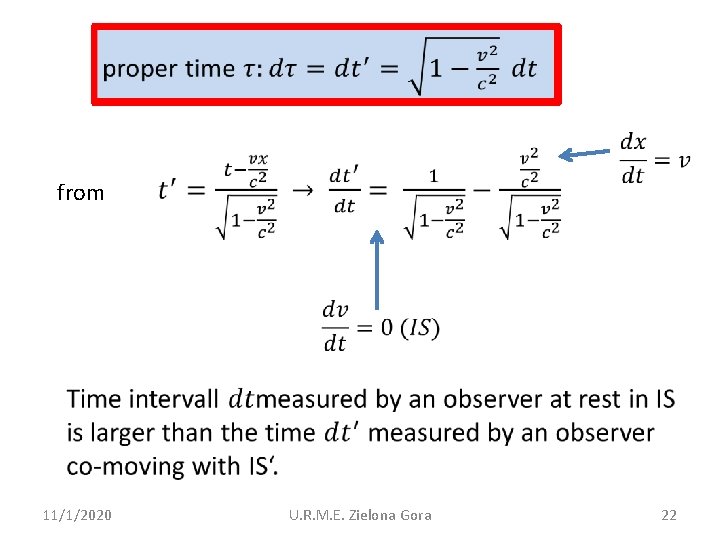
from 11/1/2020 U. R. M. E. Zielona Gora 22

Proper time (even easier): Time in the clock in motion runs slower. 11/1/2020 U. R. M. E. Zielona Gora 23

11/1/2020 U. R. M. E. Zielona Gora 24

Length measured by an observer at rest in IS is smaller then the length measured by an observer co-moving with IS‘. 11/1/2020 U. R. M. E. Zielona Gora 25

Behaviour of the 4 -D volume element under LT: The 4 -D volume element is lorentzinvariant! 11/1/2020 U. R. M. E. Zielona Gora 26

11/1/2020 U. R. M. E. Zielona Gora 27

Observation of SR effects: even if they move with ~ c, they can travel almost ~ 600 m 11/1/2020 U. R. M. E. Zielona Gora

Are the Maxwell eqs. lorentzinvariant? 11/1/2020 U. R. M. E. Zielona Gora 28

second derivatives: Maxwell eqs. Forminvariant under LT. 1 11/1/2020 U. R. M. E. Zielona Gora 29