Einstein Model for the Vibrational Heat Capacity of

Einstein Model for the Vibrational Heat Capacity of Solids

Einstein Model: Vibrational Heat Capacity of Solids • Starting as early as the late 1600’s, people started measuring the heat capacities Cp (or Cv) of various solids, liquids & gases at various temperatures. • 1819: Dulong & Petit observed that the molar heat capacity for many solids at temperatures near room temperature (300 K) is approximately independent of the material & of the temperature & is approximately R is the Ideal Gas Constant! • This result is called the “Dulong-Petit Law”

• Late 1800’s & early 1900’s: experimental capabilities became more sophisticated, & it became possible to achieve temperatures well below room temperature. • Then, measurements clearly showed that the heat capacities of solids depend on what the material is & are also strongly dependent on the temperature. In fact, at low enough temperatures, the heat capacities of many solids were observed to depend on temperature as Cv = AT 3 (A is a constant) • Early 1900’s: A theory explanation for this temperature dependence of Cv was one of the major unsolved problems in thermodynamics.

Molar Heat Capacity of a Solid • Assume that the heat supplied to a solid is transformed into kinetic & potential energies of each vibrating atom. • To explain the classical Dulong Petit Law, use a simple classical model of the vibrating solid as in the figure. Assume that each vibrating atom is an independent simple harmonic oscillator & use the Equipartition Theorem to calculate the Thermal Energy E & thus the Heat Capacity Cv 4

Molar Thermal Energy of a Solid • Dulong-Petit Law: Can be explained using the Equipartition Theorem of Classical Stat Mech: Thermal Average Energy for each degree of freedom is (½) k. T • Assume that each atom has 6 degrees of freedom: 3 translational & 3 vibrational, the Thermal Average Energy (per mole) of the vibrating solid is: R NA k 5

The Molar Vibrational Heat Capacity • Using this approximation, the Thermal Average Energy (per mole) of the vibrating solid is: (1) • By definition, the Heat Capacity of a substance at Constant Volume is (2) • Using (1) in (2) gives: In agreement with Dulong & Petit! 6

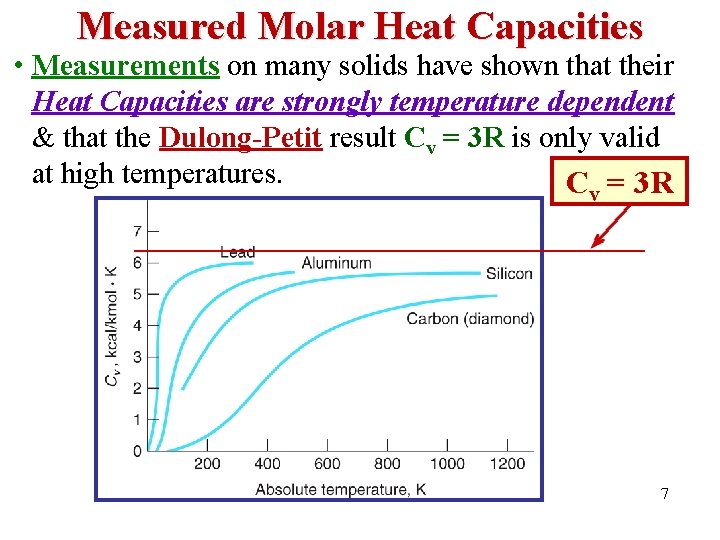
Measured Molar Heat Capacities • Measurements on many solids have shown that their Heat Capacities are strongly temperature dependent & that the Dulong-Petit result Cv = 3 R is only valid at high temperatures. C = 3 R v 7

Einstein Model of a Vibrating Solid 1907: Einstein extended Planck’s quantum ideas to solids: • He proposed that energies of lattice vibrations in a solid are quantized simple harmonic oscillators. He proposed the following model for the lattice vibrations in a solid: • Each vibrational mode is an independent oscillator • Each mode vibrates in 3 -dimensions • Each vibrational mode is a quantized oscillator with energy: or En = (n + ½ )ħ 8

• In effect, Einstein modeled one mole of solid as an assembly of 3 NA distinguishable oscillators. • He used the Canonical Ensemble to calculate the average energy of one oscillator in this model: 9

Einstein Model of a Vibrating Solid • To compute the average energy for one oscillator, note that it can be written as: where and b = 1/k. T Z is the partition function 10

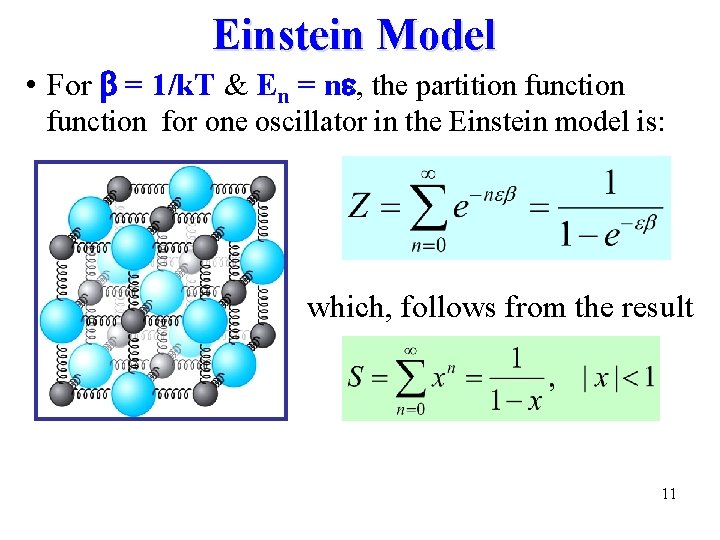
Einstein Model • For b = 1/k. T & En = n , the partition function for one oscillator in the Einstein model is: which, follows from the result 11

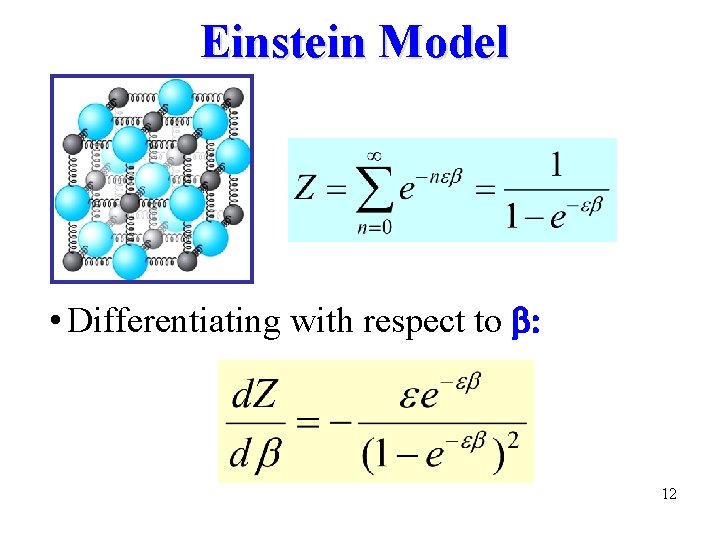
Einstein Model • Differentiating with respect to b: 12

Einstein Model …and multiplying by – 1/Z: • This is the Einstein result for the average energy of one oscillator of energy . 13

Einstein Model • Einstein’s result for the average energy of one oscillator of energy . • Einstein then made the simple (& absurd & unphysical!) assumption that each of the 3 NA oscillators vibrates at the same frequency so each has the same energy ! • With this assumption, the mean vibrational energy of the solid is just 3 NA times the above result! 14

• So, what is the frequency at which each of the 3 NA oscillators is vibrating? • In the Einstein Model this is an adjustable parameter which is fit to data & which depends on what solid is being considered. • It is usually denoted as E & is called “The Einstein Frequency” 15

• So, the molar heat capacity in Einstein’s model is: • Here TE (ħ E)/k. B is called the “Einstein temperature”. • Its not a true temperature, of course, but its an energy in temperature units. 16

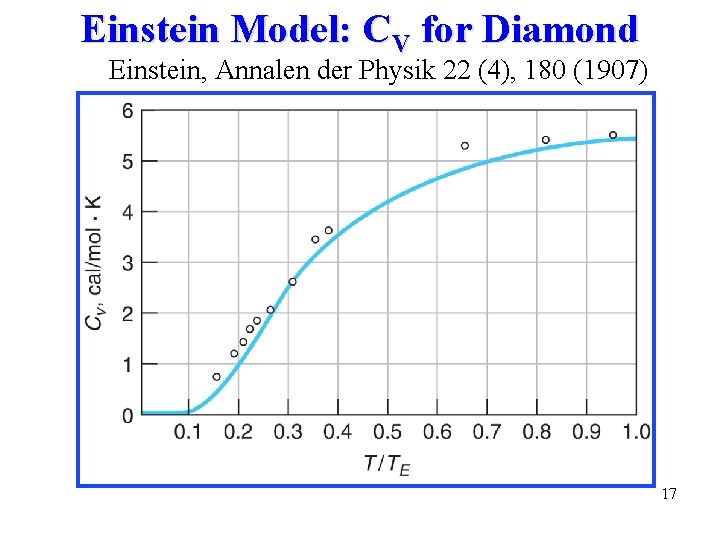
Einstein Model: CV for Diamond Einstein, Annalen der Physik 22 (4), 180 (1907) 17

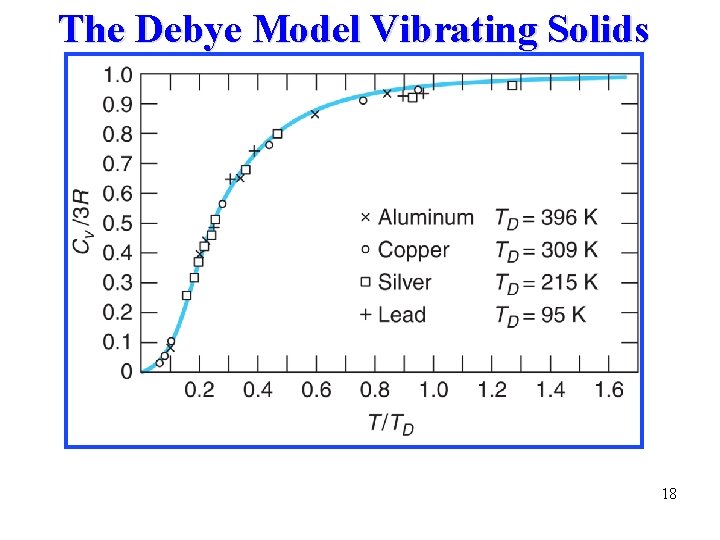
The Debye Model Vibrating Solids 18

Summary • The Dulong-Petit law is expected from the equipartition theorem of classical physics. However, it fails at temperatures low compared with the Einstein temperature • If the energy in solids is assumed to be quantized, however, models (such as Debye’s) can be developed that agree with the observed behavior of the heat capacity with temperature. Einstein was the first to suggest such a model. 19