Einstein Equations for a Star Tolman Oppenheimer Volkoff

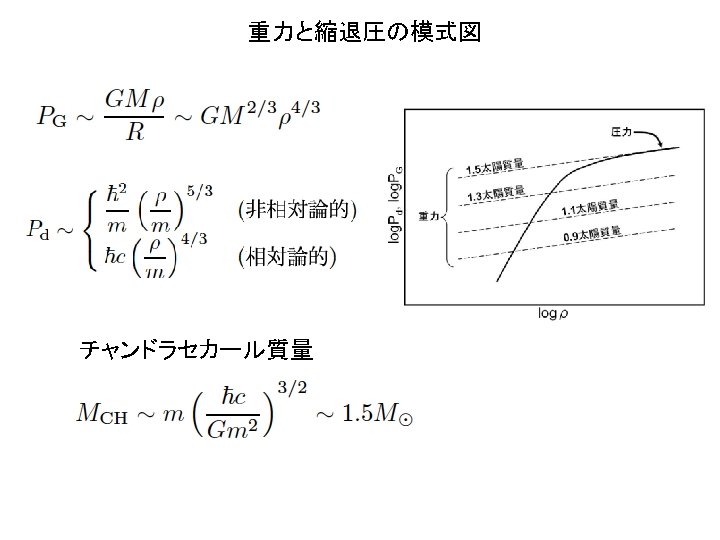
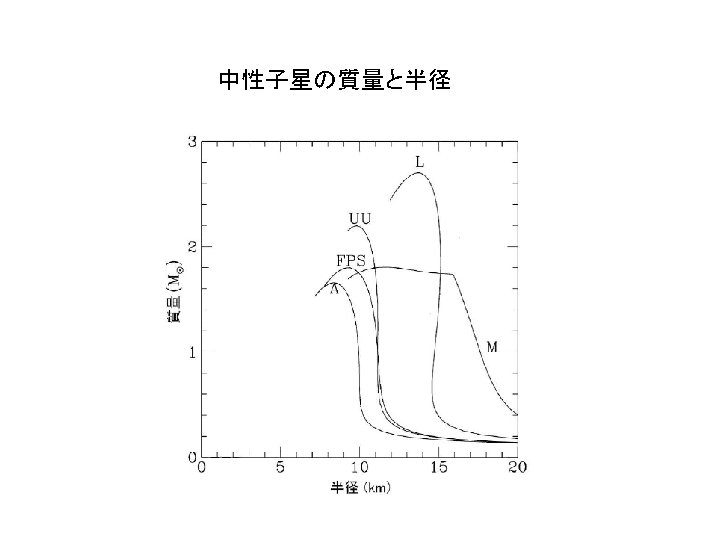
Einstein Equations for a Star Tolman. Oppenheimer. Volkoff (1939) Equation of state (nuclear force)

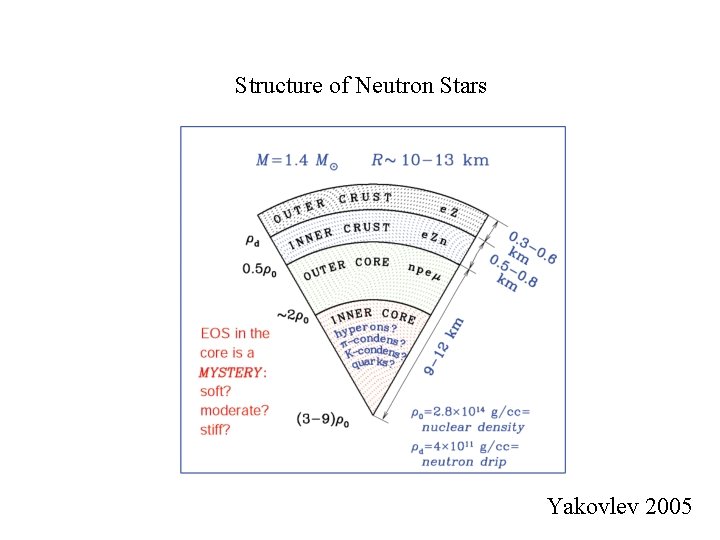
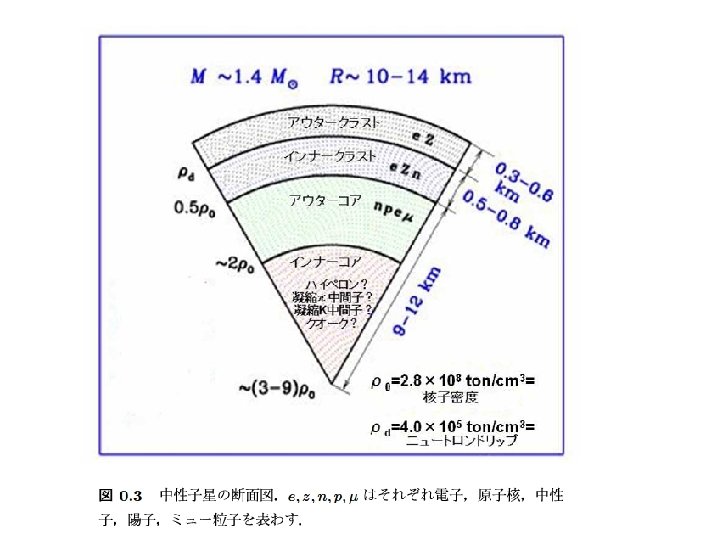
Structure of Neutron Stars Yakovlev 2005

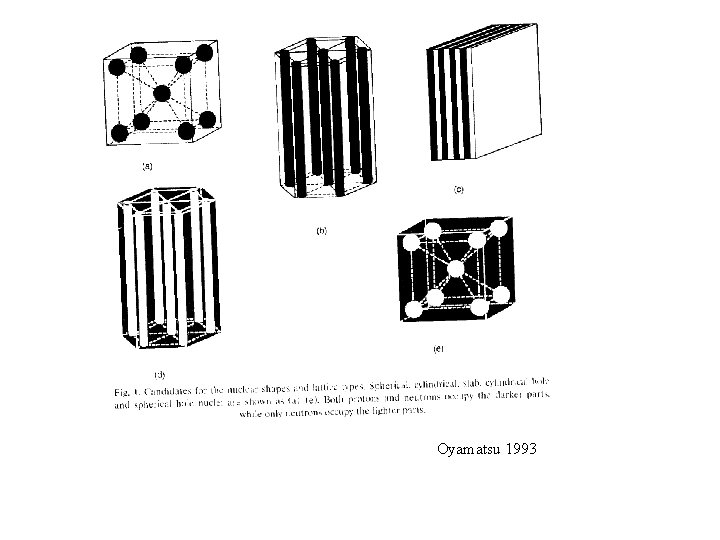
OUTER CRUST Composition: electrons + (ions) nuclei Electrons (e): constitute a strongly degenerate, almost ideal gas, give the main contribution into the pressure Ions (A, Z): fully ionized by electron pressure, give the main contribution into the density Electron background

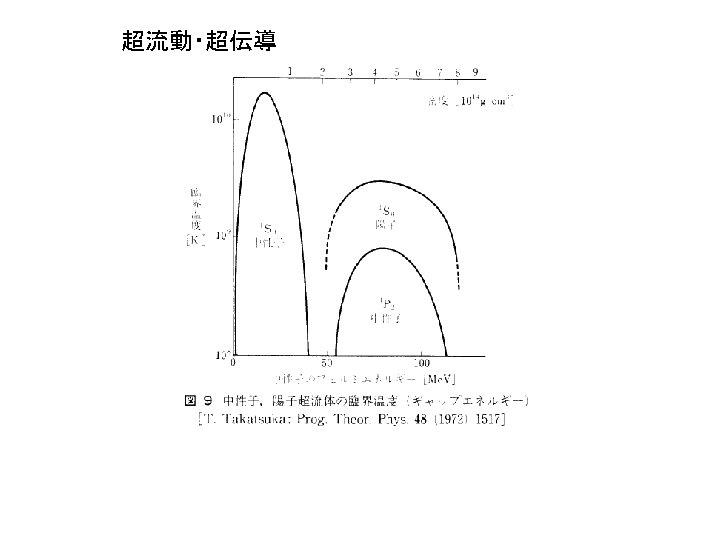
INNER CRUST Composition: electrons + nuclei + free (dripped) neutrons Electrons (e): constitute a strongly degenerate, ultra-relativistic gas Ions (A, Z): neutron-rich, occupy substantial fraction of volume e+n background Free neutrons (n): constitute a strongly degenerate Fermi-liquid, which can be superfuid

Oyamatsu 1993

OUTER CORE Composition: uniform liquid of neutrons (n), protons (p), and electrons (e), and possibly muons

INNER CORE Composition: largely unknown Hypotheses: 1. Nucleon/hyperon matter 2. Pion condensation 3. Kaon condensation 4. Quark matter 1. Nucleon-hyperon matter

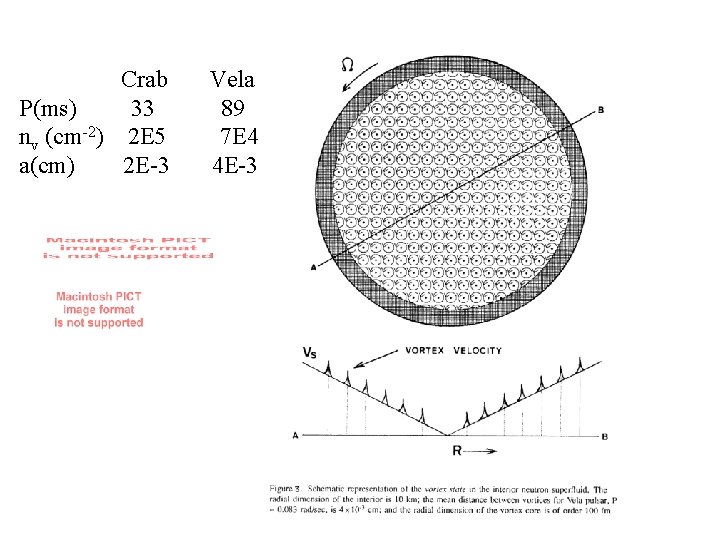
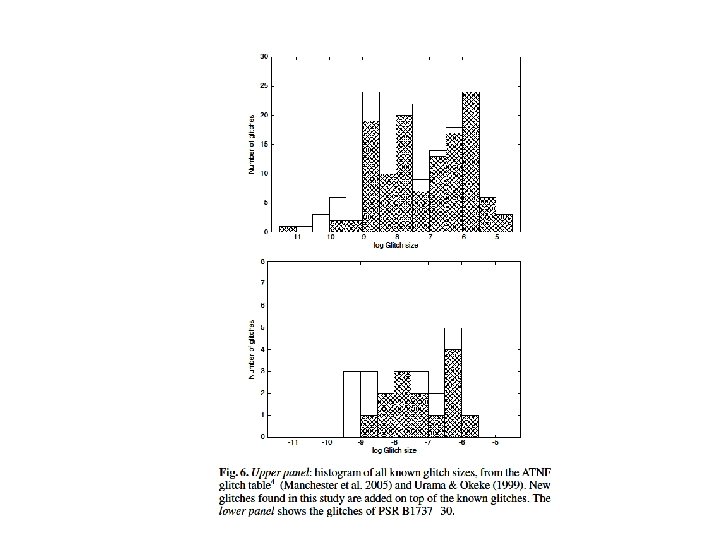
Crab P(ms) 33 nv (cm-2) 2 E 5 a(cm) 2 E-3 Vela 89 7 E 4 4 E-3

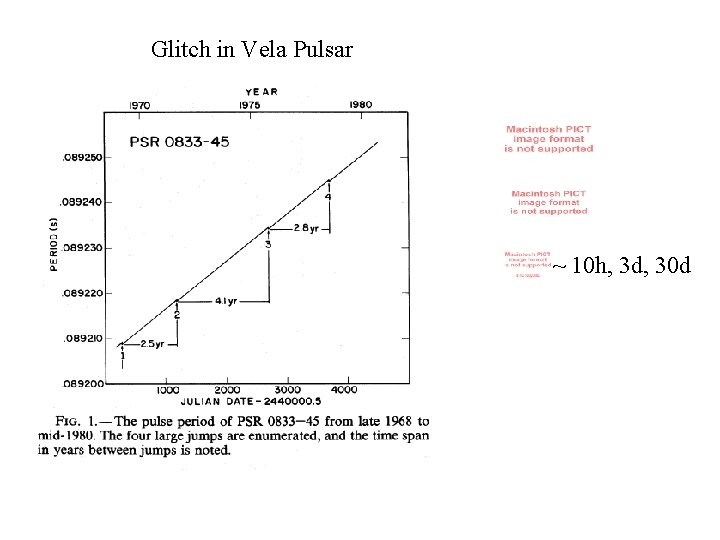
Glitch in Vela Pulsar ~ 10 h, 3 d, 30 d

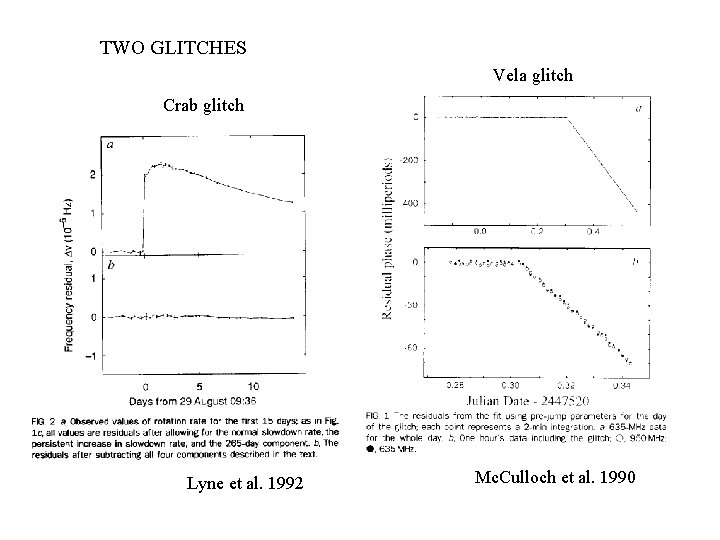
TWO GLITCHES Vela glitch Crab glitch Lyne et al. 1992 Mc. Culloch et al. 1990

Pinning energy ~1 Me. V

The Standard glitch model (Anderson & Itoh 75) Glampedakis 2008

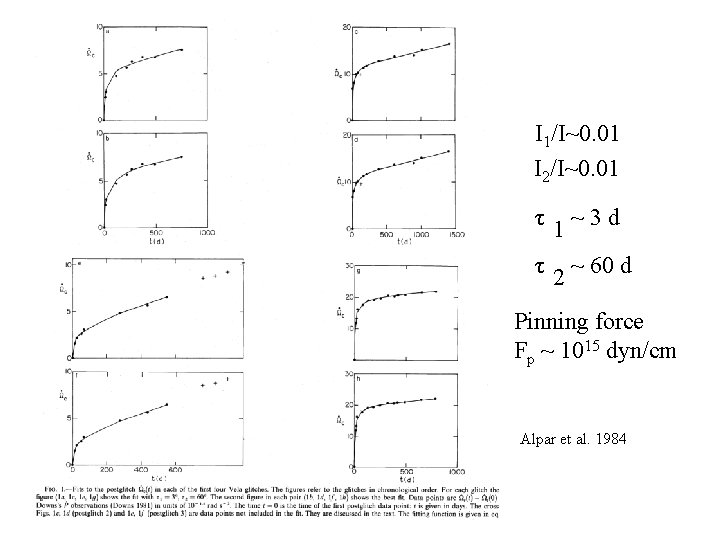
Unpinning model for a glitch Alpar et al. 1984

I 1/I~0. 01 I 2/I~0. 01 τ 1~3 d τ 2 ~ 60 d Pinning force Fp ~ 1015 dyn/cm Alpar et al. 1984

Vela pulsar ----> required

Pinning force ・condensation energy (Alpar et al. 1984) pinning energy Ep ~ 1 Me. V coherence length ξ~10 -12 cm lattice constant a ~5× 10 -12 cm ・cancellation of the elementary pinning force (Jones 1991) rigid vortex --> equal number of pinning sites on either side of the line --> fp ~ 0 ・bending of vortex lines (Link & Epstein 1993) finite tension --> kink --> much more efficient pinning

Vortex pinning

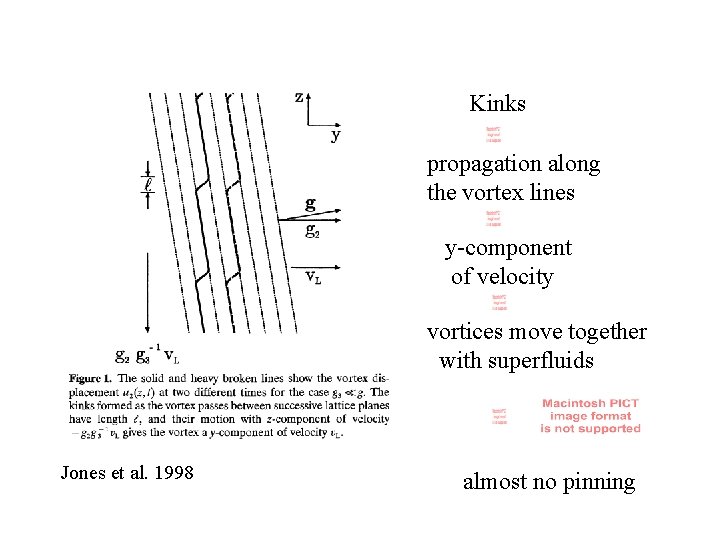
Kinks propagation along the vortex lines y-component of velocity vortices move together with superfluids Jones et al. 1998 almost no pinning

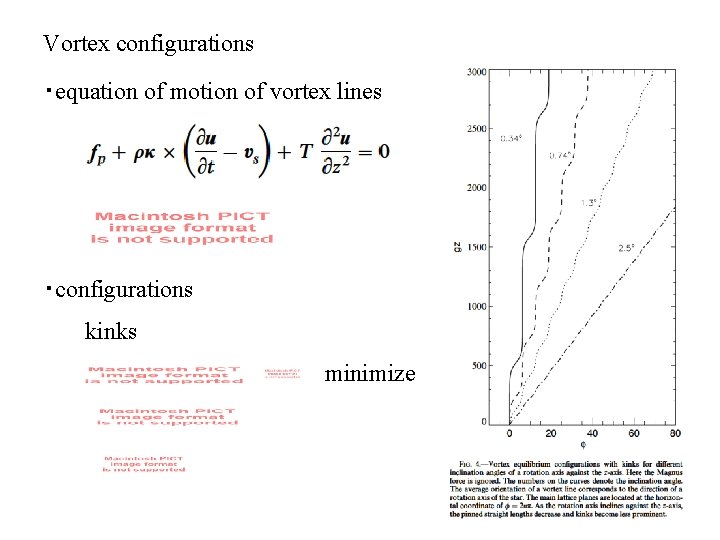
Vortex configurations ・equation of motion of vortex lines ・configurations kinks minimize

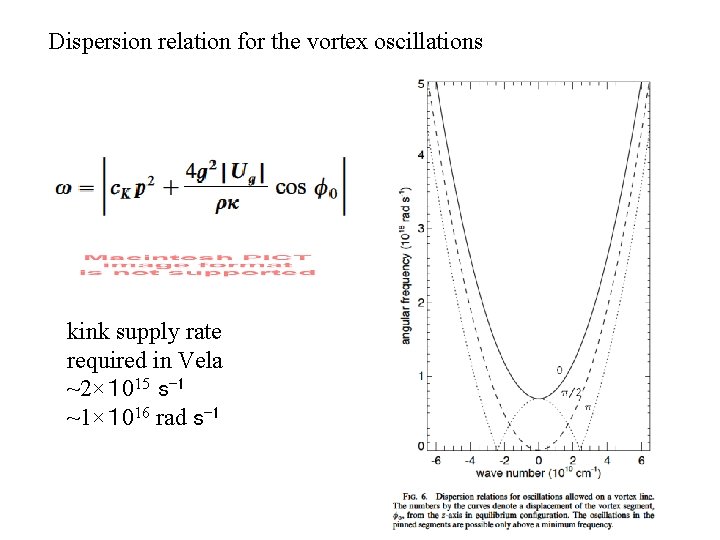
Dispersion relation for the vortex oscillations kink supply rate required in Vela ~2×１ 015 s-1 ~1×１ 016 rad s-1

Discussion on vortex pinning (1) We find no unstable mode that grows with time. The vortex (2) equilibrium configurations with static kink structures are stable. (3) Hence, the kink motion as required by Jones is less likely. (2) The kink solution can be expressed as a sum of fourier components of different wave numbers. The dispersion relation shows that the phase velocity of vortex waves depends on the wave number. Hence, even if a kink is formed and start to move, the kink feature will be smeared out during propagation. (3) The vortex equilibrium configuration is composed of the static kink and straight segments. A vortex line in equilibrium lies deep in the pinning potential well and is strongly pinned to the lattice nuclei in its most part, especially when the vortex line is close to the main axis of a crystal lattice. Pinning may be strong enough to explain the large glitches observed in Vela pulsar.

Glampedakis & Andersson 2008