Eigenspannungen Eigenspannungen Analyse von Eigenspannungen in kristallinen Materialien

Eigenspannungen

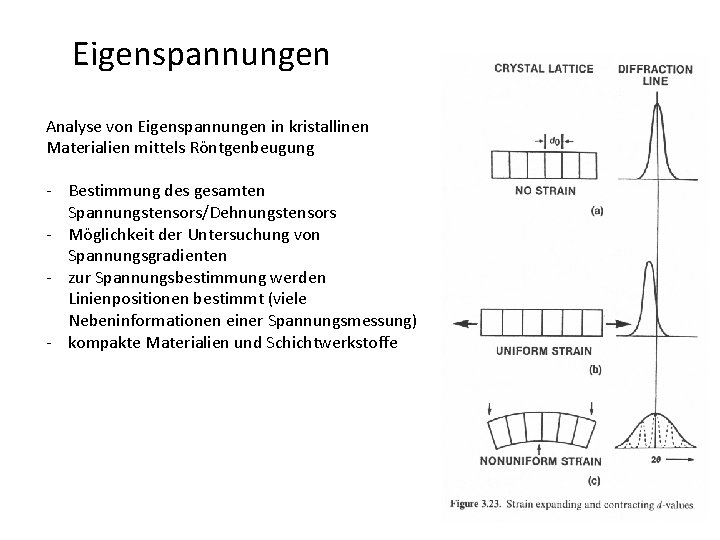
Eigenspannungen Analyse von Eigenspannungen in kristallinen Materialien mittels Röntgenbeugung - Bestimmung des gesamten Spannungstensors/Dehnungstensors - Möglichkeit der Untersuchung von Spannungsgradienten - zur Spannungsbestimmung werden Linienpositionen bestimmt (viele Nebeninformationen einer Spannungsmessung) - kompakte Materialien und Schichtwerkstoffe

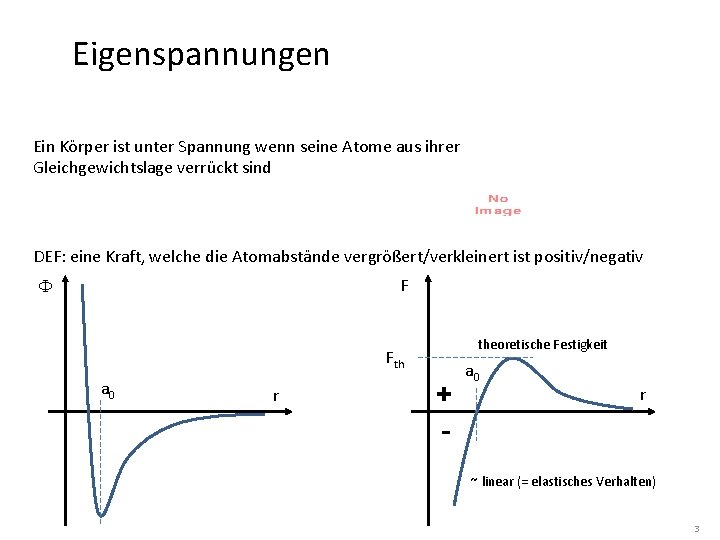
Eigenspannungen Ein Körper ist unter Spannung wenn seine Atome aus ihrer Gleichgewichtslage verrückt sind DEF: eine Kraft, welche die Atomabstände vergrößert/verkleinert ist positiv/negativ F F theoretische Festigkeit Fth a 0 r + - a 0 r ~ linear (= elastisches Verhalten) 3

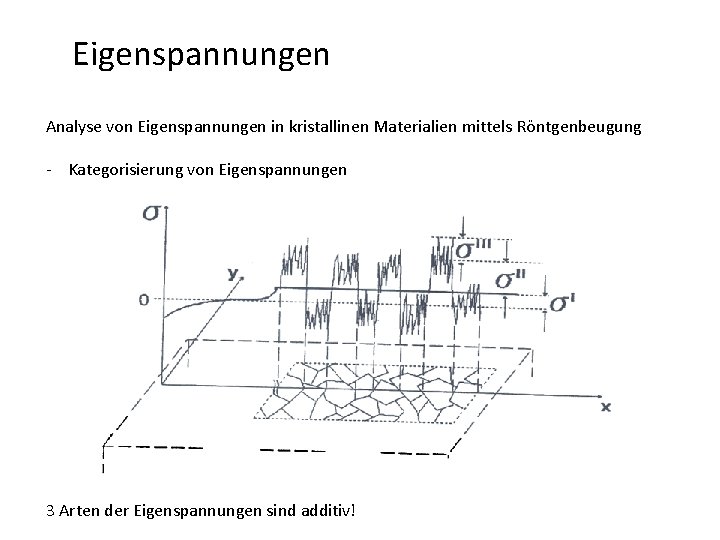
Eigenspannungen Analyse von Eigenspannungen in kristallinen Materialien mittels Röntgenbeugung - Kategorisierung von Eigenspannungen 3 Arten der Eigenspannungen sind additiv!

Eigenspannungen Ursachen von Eigenspannungen - Gittermisfit an Grenzflächen verschiedene thermische Ausdehnungskoeffizienten von Phasen Materialbearbeitung (z. B. Oberflächenbehandlung) Schweißen Beschichtungen Verformung (in situ) 5

Eigenspannungen Spannung und Dehnung sind tensorielle Eigenschaften http: //www. maschinenbau-wissen. de/skript 3/mechanik/festigkeitslehre/116 -spannungstensor 6

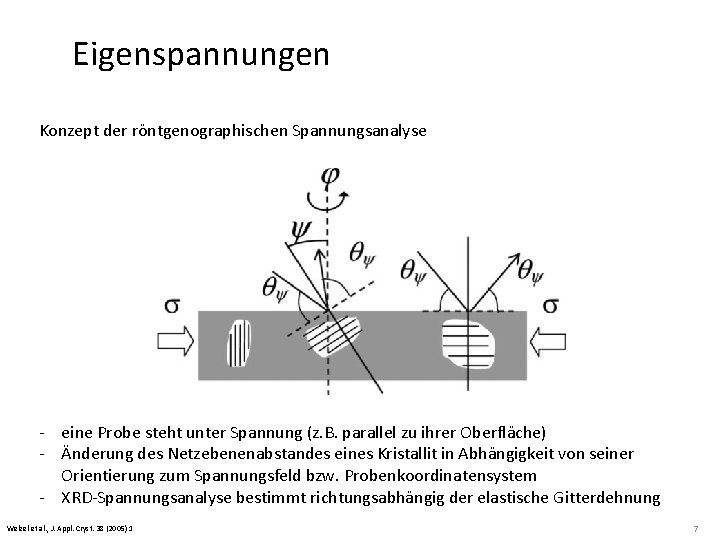
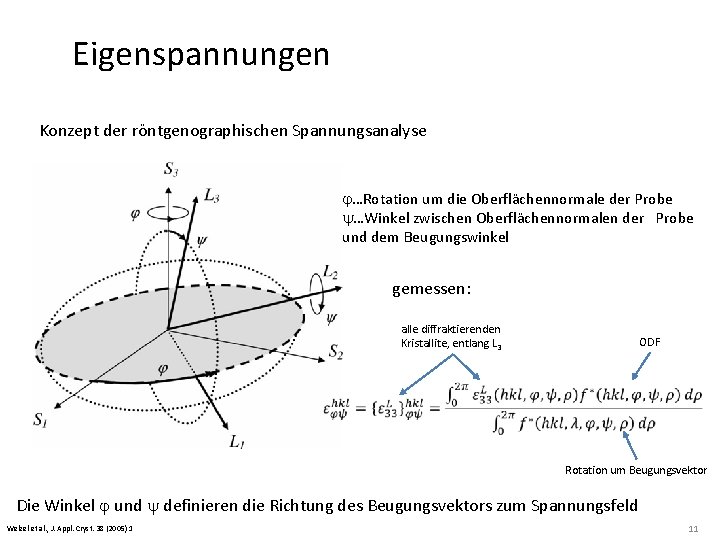
Eigenspannungen Konzept der röntgenographischen Spannungsanalyse - eine Probe steht unter Spannung (z. B. parallel zu ihrer Oberfläche) - Änderung des Netzebenenabstandes eines Kristallit in Abhängigkeit von seiner Orientierung zum Spannungsfeld bzw. Probenkoordinatensystem - XRD-Spannungsanalyse bestimmt richtungsabhängig der elastische Gitterdehnung Welzel et al. , J. Appl. Cryst. 38 (2005) 1 7

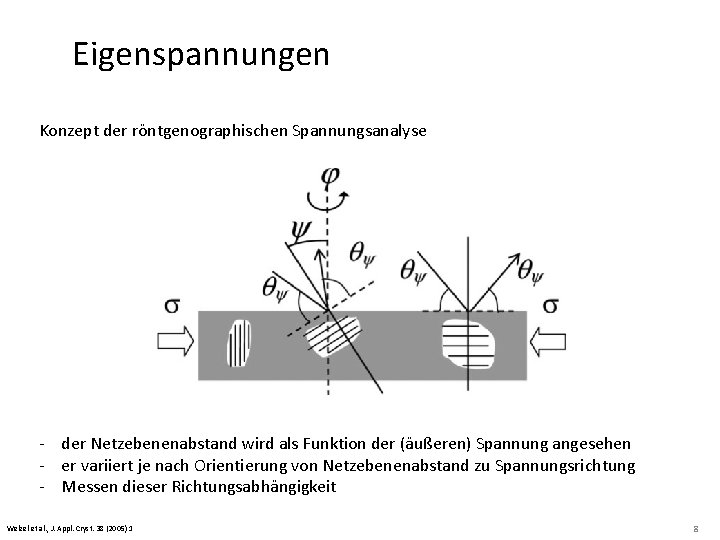
Eigenspannungen Konzept der röntgenographischen Spannungsanalyse - der Netzebenenabstand wird als Funktion der (äußeren) Spannung angesehen - er variiert je nach Orientierung von Netzebenenabstand zu Spannungsrichtung - Messen dieser Richtungsabhängigkeit Welzel et al. , J. Appl. Cryst. 38 (2005) 1 8

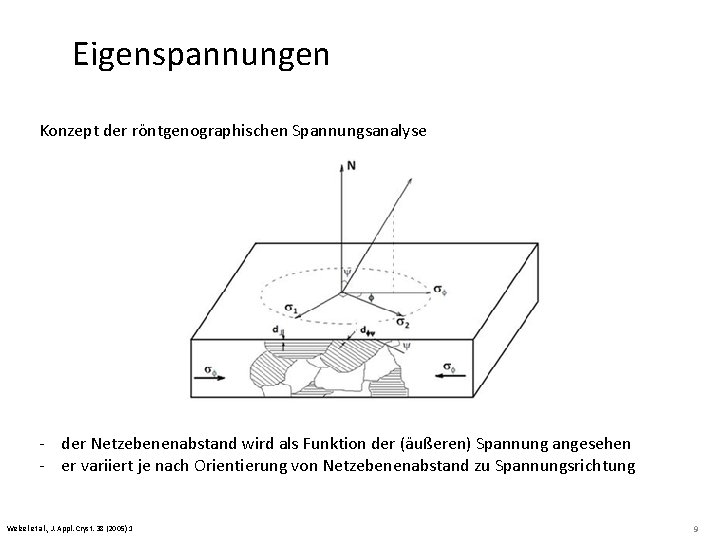
Eigenspannungen Konzept der röntgenographischen Spannungsanalyse - der Netzebenenabstand wird als Funktion der (äußeren) Spannung angesehen - er variiert je nach Orientierung von Netzebenenabstand zu Spannungsrichtung Welzel et al. , J. Appl. Cryst. 38 (2005) 1 9

Eigenspannungen Konzept der röntgenographischen Spannungsanalyse - Messen der Position einer hkl-Linie - Definition der Eigenspannung I. Art - Netzebenenabstände werden immer entlang der Richtung des Beugungsvektors bestimmt (Netzebenen liegen senkrecht dazu) - nur ein bestimmter Anteil der Kristallite wird untersucht - daher: Eigenspannungen aus mechanischer Messung verschieden von den XRDWerten Welzel et al. , J. Appl. Cryst. 38 (2005) 1 10

Eigenspannungen Konzept der röntgenographischen Spannungsanalyse j…Rotation um die Oberflächennormale der Probe y…Winkel zwischen Oberflächennormalen der Probe und dem Beugungswinkel gemessen: alle diffraktierenden Kristallite, entlang L 3 ODF Rotation um Beugungsvektor Die Winkel j und y definieren die Richtung des Beugungsvektors zum Spannungsfeld Welzel et al. , J. Appl. Cryst. 38 (2005) 1 11

Eigenspannungen Grundlegende Zusammenhänge – isotrope Kristallite - Vielkristall, aus elastisch isotropen Kristalliten aufgebaut - elastische Eigenschaften des makroskopischen Vielkristalls sind gleich denen eines einzelnen, mechanisch isotropen Kristallits Dehnung aller Kristallite entlang des Beugungsvektors Rotation des Probenkoordinatensystems in Laborkoordinatensystem - Zusammenhang zwischen Dehnung und Spannung für Vielkristalle, die aus elastisch isotropen Kristalliten aufgebaut sind 12

Eigenspannungen Grundlegende Zusammenhänge – isotrope Kristallite - das sin 2 y-Gesetz - gilt für Dehnung aus Beugungmessung sowie mechanischen Messungen - bei homogenem Spannungsfeld und elastisch isotropen Kristalliten auch gültig bei Vorhandensein von Texturen 13

Eigenspannungen Grundlegende Zusammenhänge – anisotrope Kristallite - Realität: Kristallite in Vielkristallen sind elastisch anisotrop - Spannungen und Dehnungen variieren von Kristallit zu Kristallit aufgrund unterschiedlicher relativer Orientierung von Kristallit und Spannungsfeld - resultierende Spannung/Dehnung ergibt sich aus Kornwechselwirkungsmodellen - quasi-isotrope Probe: gesamte Probe ist elastisch isotrop, obwohl alle Kristallite elastisch anisotrop sind - keine Textur !!!! - Kornwechselwirkung ist richtungsunabhängig - bei Quasiisotropie werden röntgenographischen elastischen Konstanten (XEC = S 1, ½S 2) genutzt - für makroskopisch anisotrope Proben müssen röntgenographische Spannungsfaktoren (XSF) genutzt werden 14

Eigenspannungen Grundlegende Zusammenhänge – anisotrope Kristallite - das sin 2 y-Gesetz, unterschiedet sich vom isotropen Fall nur hinsichtlich der XEC - XEC‘s sind nun vom der jeweils beugenden Netzebenenfamilie abhängig und vom gewählten Kornwechselwirkungsmodell - ermittelte Spannungen/Dehnung unterscheiden sich von mechanischen Werten - sin 2 y-Methode ist für alle Spannungszustände in quasiisotropen Vielkristallen anwendbar 15

Eigenspannungen Kornwechselwirkungmodelle - Berechnung der XEC‘s oder XSF‘s - Messung dieser ist möglich (Dehnungsmessung unter bekannter äußerer Spannung) - meist gerechnet aus den elastischen Konstanten der Einkristalle - Hooke‘sches Gesetz Einsteinsche Summenkonvention - 6 unabhängige Gleichungen - 12 unabhängige Komponenten - Lösen eines linearen Gleichungssystems, wenn 6 der unabhängigen Komponenten bekannt sind - Annahmen: 6 der Spannungs-/Dehnungskomponenten sind äquivalent zu den über alle Kristallite gemittelten mechanischen Werten 16

Eigenspannungen Kornwechselwirkungmodelle – Voigt-Modell - Annahme: homogene Dehnungsverteilung (konstante Dehnung) - erzeugt Spannungssprünge an Korngrenzen, die das mechanische Gleichgewicht verletzen - nicht kompatibel mit der Realität - es ergeben sich längliche Ausdrücke je nach Kristallsystem - z. B. kubisch: - XEC‘s nach Voigt haben keine hkl-Abhängigkeit 17

Eigenspannungen Kornwechselwirkungmodelle – Reuss-Modell - Annahme: homogene Spannungsverteilung (konstante Spannung) - Dehnungsinhomogenitäten an Korngrenzen (Kristall würde auseinanderfallen) - nicht kompatibel mit der Realität - es ergeben sich längliche Ausdrücke je nach Kristallsystem - z. B. kubisch: - XEC‘s nach Reuss sind hkl-abhängig 18

Eigenspannungen Kornwechselwirkungmodelle – Eshelby-Kröner-Modell - Annahme: ein Kristallit ist in einer homogenen Matrix eingebettet, welche die Eigenschaften des gesamten Polykristalls hat - Ausdruck über den „Mismatch“ der elastischen Eigenschaften des Einschlusses zu denen der Matrix (wichtig: Mittelung der Abweichungen über alle Kristallite = 0 iterative Lösung) - Spannungen/Dehnungen in einem eingebetteten, kugelförmigen Einschluß müssen berechnet werden - analytische Lösungen nur für isotrope Matrizes - Erweiterungen für texturierte Proben (keine analytische Lösung) - wird generell als das Modell angesehen, welches am ehesten realen Proben entspricht 19

Eigenspannungen Kornwechselwirkungmodelle – Vook-Witt-Modell - spezielles Modell für Schichten Annahme: ein Kristallit ist in 3 Dimensionen von anderen Kristalliten umgeben 2 Extremfälle für Kornwechselwirkungsmodelle (Voigt, Reuss) Schichten haben reduzierte Dimensionalität - Vook-Witt-Modell: makroskopische transverse Isotropie (in der Schichtebene) - Dehnung ist rotationssymmetrisch in Schichtebene - Dehnung ist für alle Kristallite gleich (V) - Spannungen senkrecht zur Schicht verschwinden (R) - inverses Vook-Witt-Modell: - Spannung ist rotationssymmetrisch in Schichtebene - Spannung ist für alle Kristallite gleich (R) - Dehnung senkrecht zur Schichtebene ist für alle Kristallite gleich (V) 20

Eigenspannungen Kornwechselwirkungmodelle – Neerfeld-Hill-Modell (effektive Kornwechselwikrung) - XEC‘s aus extremen Kornwechselwirkungsmodellen entsprechen nicht der Realität - Mittelung dieser Extremfälle sind deutlich besser: ein Teil der Kristallite gehorcht einem Extremfall, ein Teil der Kristallite einem anderen - Neerfeld-Hill: Mittelung aus Voigt- und Reuss-Modell für kompakte Polykristalle - empirisch: arithmetisches oder geometrisches Mittel aus V oder R - Wichtung: ½ - Wichtung kann auch Anpassungsparameter sein 21

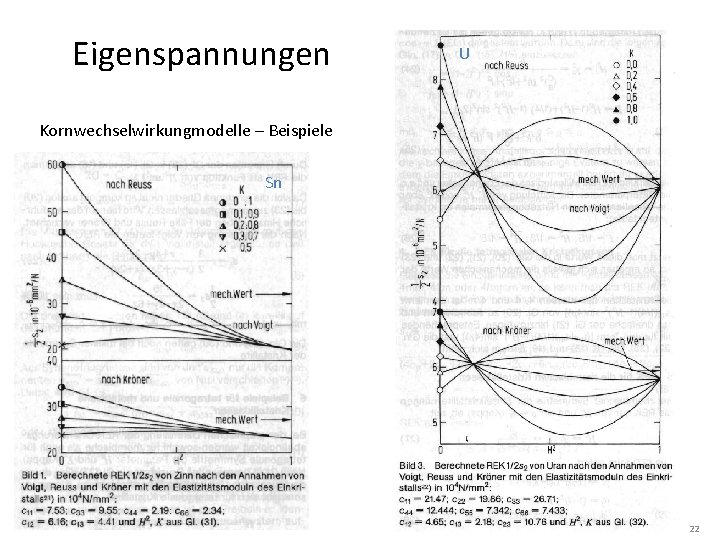
Eigenspannungen U Kornwechselwirkungmodelle – Beispiele Sn 22

Eigenspannungen Kornwechselwirkungmodelle – Beispiele Kröner 1/2 S 2 [mm 2/N] -S 1 [mm 2/N] 23

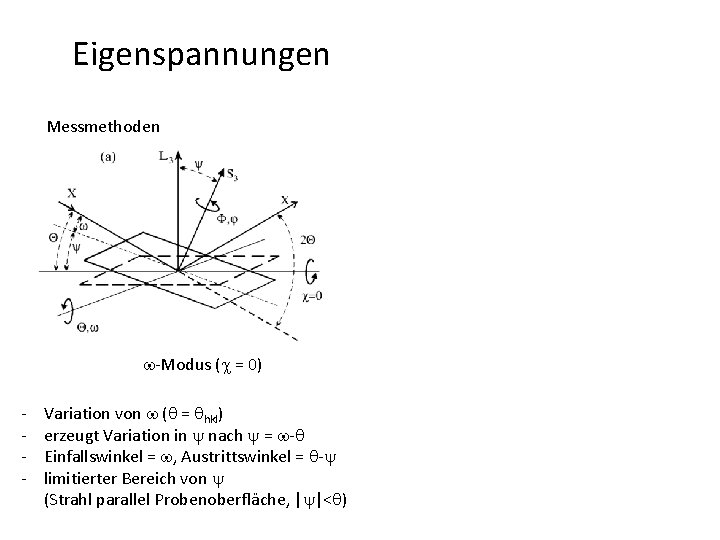
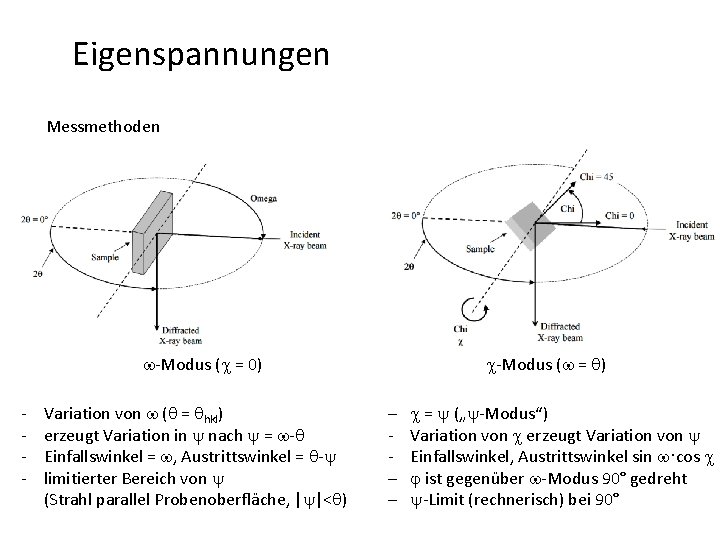
Eigenspannungen Messmethoden - Winkel y bestimmt die Messrichtung bzgl. der Oberflächennormalen - y, j beschreiben Orientierung der {hkl}-Netzebenennormalen bzgl. des Probenkoordinatensystems (sin 2 y-Gleichung) - f, w, c (Winkel des Instruments) beschreiben die Probenorientierung bzgl. des Laborkoordinatensystems - 2 q bringt definierte {hkl}-Netzebene in Reflexionsstellung

Eigenspannungen Messmethoden w-Modus (c = 0) - Variation von w (q = qhkl) erzeugt Variation in y nach y = w-q Einfallswinkel = w, Austrittswinkel = q-y limitierter Bereich von y (Strahl parallel Probenoberfläche, |y|<q)

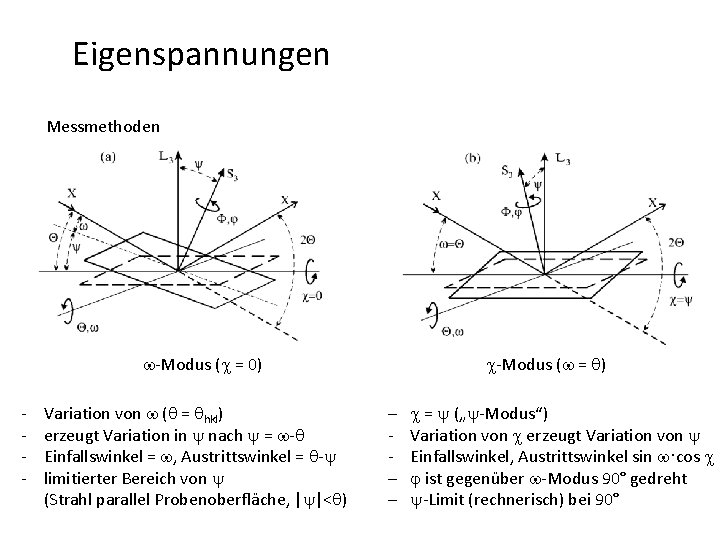
Eigenspannungen Messmethoden w-Modus (c = 0) - Variation von w (q = qhkl) erzeugt Variation in y nach y = w-q Einfallswinkel = w, Austrittswinkel = q-y limitierter Bereich von y (Strahl parallel Probenoberfläche, |y|<q) c-Modus (w = q) - c = y („y-Modus“) Variation von c erzeugt Variation von y Einfallswinkel, Austrittswinkel sin w·cos c j ist gegenüber w-Modus 90° gedreht y-Limit (rechnerisch) bei 90°

Eigenspannungen Messmethoden w-Modus (c = 0) - Variation von w (q = qhkl) erzeugt Variation in y nach y = w-q Einfallswinkel = w, Austrittswinkel = q-y limitierter Bereich von y (Strahl parallel Probenoberfläche, |y|<q) c-Modus (w = q) - c = y („y-Modus“) Variation von c erzeugt Variation von y Einfallswinkel, Austrittswinkel sin w·cos c j ist gegenüber w-Modus 90° gedreht y-Limit (rechnerisch) bei 90°

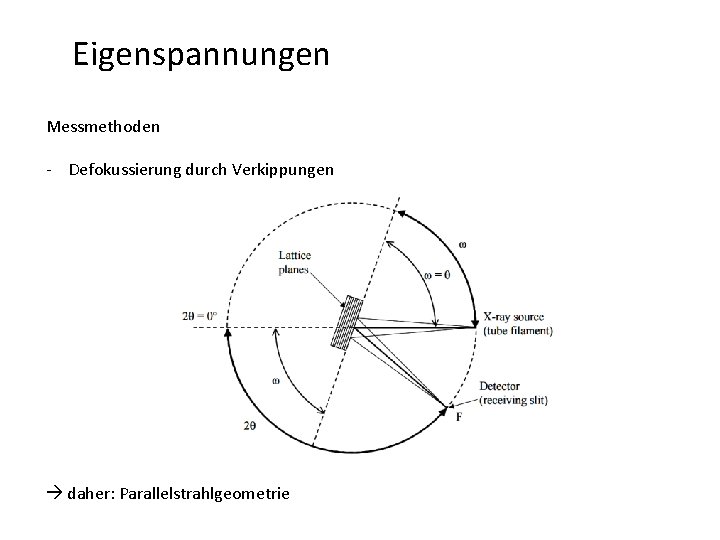
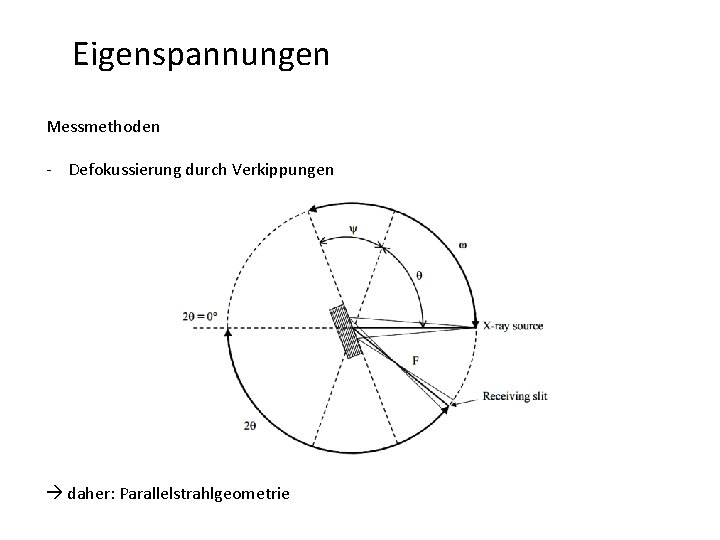
Eigenspannungen Messmethoden - Defokussierung durch Verkippungen daher: Parallelstrahlgeometrie

Eigenspannungen Messmethoden - Defokussierung durch Verkippungen daher: Parallelstrahlgeometrie

Eigenspannungen Messmethoden - Methode des streifenden Einfalls - besonders zur Eigenspannungsmessung in dünnen Schichten/Oberflächenbereichen - Methode mit konstanter Eindringtiefe (Spannungs-Tiefen-Profile) - Einfallswinkel fixiert (Eindringtiefe!) weniger Freiheit zur Variation von y - Multiple c: Einfallswinkel w klein, Variation von c erzeugt Variation in y (Kombination von w- und c-Modus) - Multiple {hkl}: Einfallswinkel w klein, c = 0, Variation in 2 q erzeugt Variation in y nach y = qhkl-w (y, qhkl nicht unabhängig voneinander) - Multiple l: Wechsel der Wellenlänge ändert qhkl und damit y, Einfallswinkel muss auf Energie der Strahlung korrigiert werden

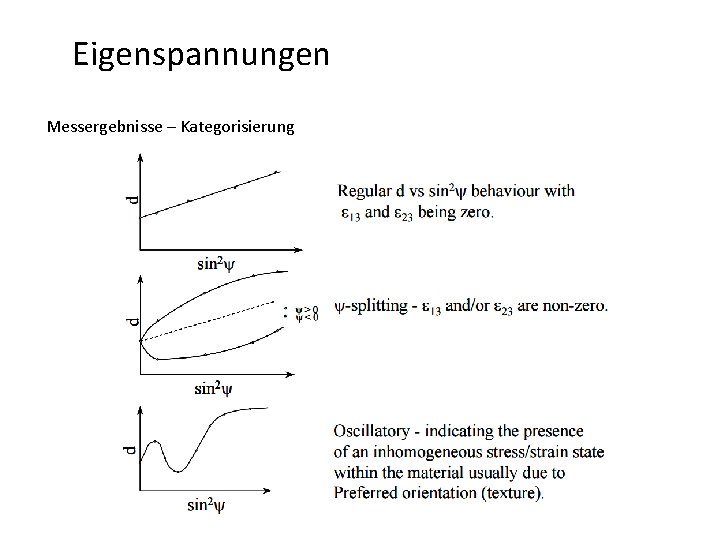
Eigenspannungen Messergebnisse – Kategorisierung

Eigenspannungen Auswertemethoden: makroskopisch elastisch isotrope Körper - Bestimmen der Gitterdehnung in einer Messrichtung (y, j) bzgl. der Komponenten des Spannungstensors im Probenkoordinatensystem - theoretisch 6 unabhängige Komponenten des Spannungstensors, d. h. Spannungen müssen mindestens in 6 unabhängigen Richtungen gemessen werden (Lösen eines linearen Gleichungssystems) - traditionell: Umstellen des sin 2 y-Gesetzes, so dass die Komponenten des Spannungstensors aus den Anstiegen/Ordinatenschnittpunkten linearer Regressionen bestimmter Funktionen von j, y, hkl bestimmt werden können - single {hkl} oder multiple {hkl} - Methode der kleinsten Quadrate

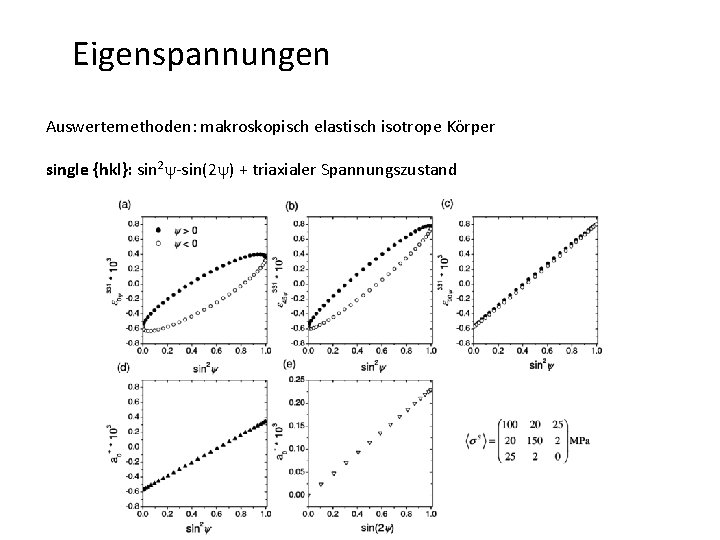
Eigenspannungen Auswertemethoden: makroskopisch elastisch isotrope Körper single {hkl}: sin 2 y-sin(2 y) + triaxialer Spannungszustand

Eigenspannungen Auswertemethoden: makroskopisch elastisch isotrope Körper single {hkl}: sin 2 y-sin(2 y) + tiaxialer Spannungszustand - für generelle Spannungszustände sind Abhängigkeiten von sin 2 y / sin(2 y) nichtlinear - Linearisierung durch: vs. sin 2 y vs. sin(2 y) j = (0°, 45°, 90°)

Eigenspannungen Auswertemethoden: makroskopisch elastisch isotrope Körper single {hkl}: sin 2 y-sin(2 y) + tiaxialer Spannungszustand - für generelle Spannungszustände sind Abhängigkeiten von sin 2 y / sin(2 y) nichtlinear - aus den 3 j (0°, 45°, 90°) ergeben sich 3 Anstiege (Ai) für a+j - zusätzliche Bedingung für 4. Spannungskomponente in a+j aus ej 0 hkl

Eigenspannungen Auswertemethoden: makroskopisch elastisch isotrope Körper - meist nicht erforderlich - reduzierter Messaufwand bei (erwarteten) einfacheren Spannungszuständen - biaxialer Spannungszustand: j = (0, 45°, 90°) ausreichend, aj- nicht erforderlich - rotationssymmetrischer, biaxialer Spannungszustand (dünne Schichten) keine j-Abhängigkeit vor allem für Methoden des streifenden Einfalls genutzt, Messung mehrerer {hkl}

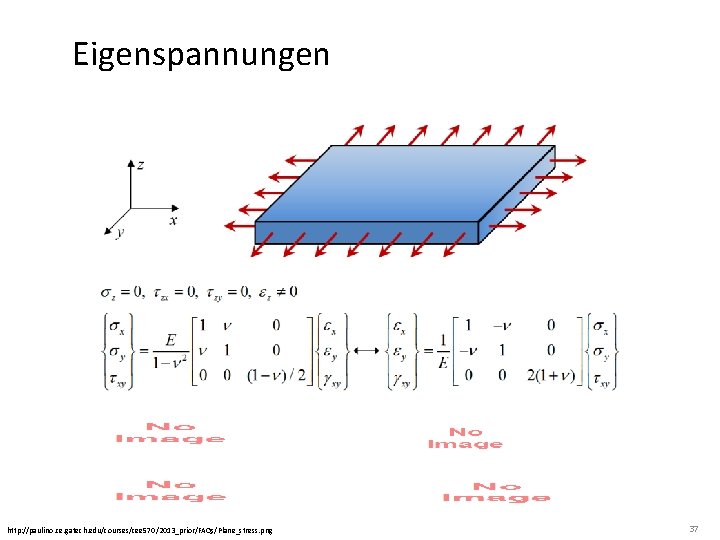
Eigenspannungen http: //paulino. ce. gatech. edu/courses/cee 570/2013_prior/FAQs/Plane_stress. png 37

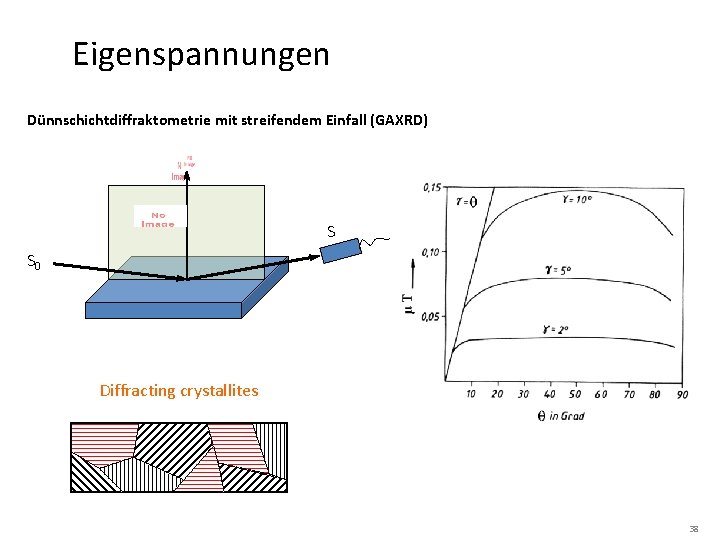
Eigenspannungen Dünnschichtdiffraktometrie mit streifendem Einfall (GAXRD) S S 0 Diffracting crystallites 38

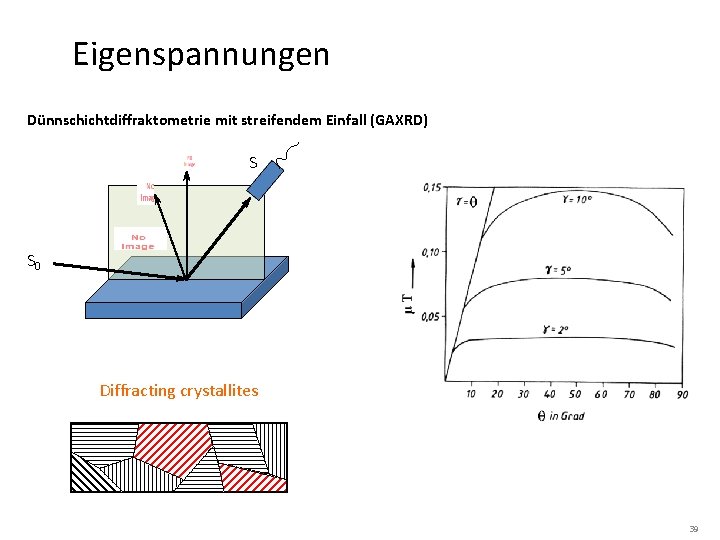
Eigenspannungen Dünnschichtdiffraktometrie mit streifendem Einfall (GAXRD) S S 0 Diffracting crystallites 39

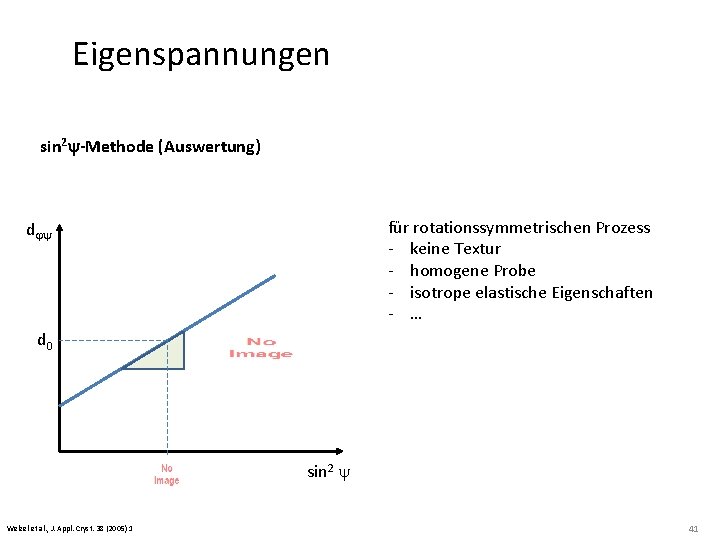
Eigenspannungen sin 2 y-Methode im principle reference frame: PLANE STRESS ergibt eine Gerade für konstante j, vs. aus deren Anstieg sich die Spannung ableiten lässt Welzel et al. , J. Appl. Cryst. 38 (2005) 1 40

Eigenspannungen sin 2 y-Methode (Auswertung) für rotationssymmetrischen Prozess - keine Textur - homogene Probe - isotrope elastische Eigenschaften - … djy d 0 Welzel et al. , J. Appl. Cryst. 38 (2005) 1 sin 2 y 41

Eigenspannungen Fehlereinflüsse - Fehler in der Eigenspannungsmessung - Bestimmung von d 0 hkl, spannungsfreiem Netzebenenabstand mitunter kompliziert - es gibt theoretisch berechenbare Richtungen (j, y) bei denen die Probe spannungsfrei ist biaxialer, rotationssymmetrischer Spannungszustand - sehr genaue Kenntnis von d 0 hkl für Bestimmung von s. S 33 nötig

Eigenspannungen Fehlerarten - Fehler I. Art: unabhängig von y - Messen von Peakverschiebung gut möglich, keine absolute Peakposition - instrumentelle Fehler: Nullpunktverschiebung, Fehljustage der Euler-Wiege - tritt auf bei Messung einer {hkl} oder multiple {hkl}, hier Dd/d = const. - Fehler II. Art: abhängig von y - weder Peakposition noch Peakverschiebung messbar - instrumentelle Fehler: v. a. Probenposition (z), Primärstrahlfehljustage - bei Messung einer {hkl} ohne Bedeutung (Messung relativer Dehnungen) - bei Methoden der kleinsten Quadrate keine Bedeutung (wenn d 0 Parameter ist)

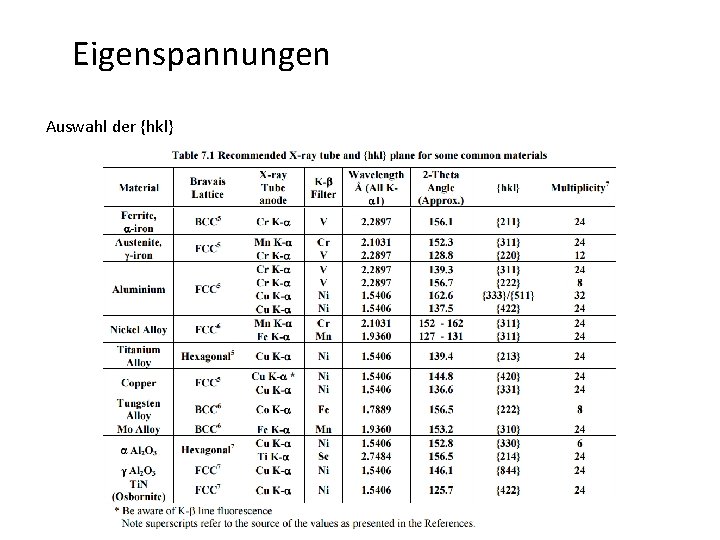
Eigenspannungen Auswahl der {hkl}