Eigen Taste A Constant Time Collaborative Filtering Algorithm

Eigen. Taste: A Constant Time Collaborative Filtering Algorithm Ken Goldberg Students: Theresa Roeder, Dhruv Gupta, Chris Perkins Industrial Engineering and Operations Research Electrical Engineering and Computer Science UC Berkeley

CF Problem Definition • A set of objects (movies, books, jokes) • A user rates a subset of objects • Based on the ratings, retrieve objects from the complement of this subset. Criteria: – Effective : recommended objects should receive high ratings – Efficient : the online recommendation process should run quickly and be scalable

Some Previous Work • D. Goldberg, et al. - Tapestry (1992) • Riedel, Resnick, Konstan et. al. Group. Lens(1994 -) • Shardanand Maes - Ringo (1995) • Resnick and Varian (1997) • Breese et. al. at Microsoft Research (1998) • Pazzani (1999) • Herlocker et. al. - Group. Lens (1999)

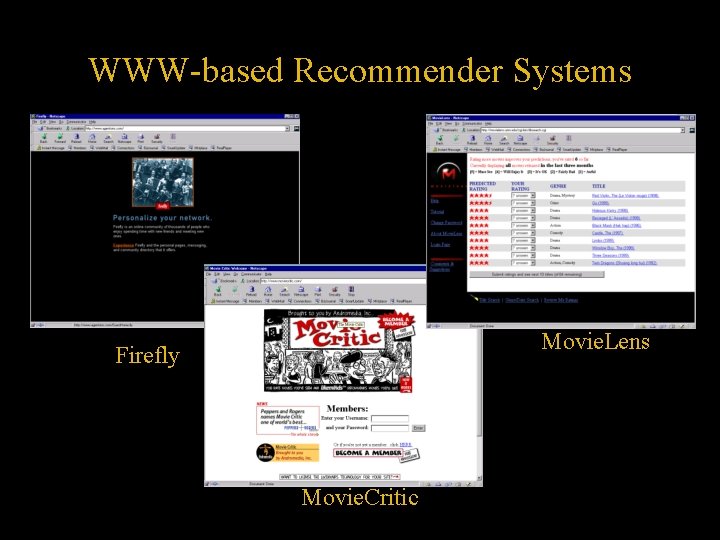
WWW-based Recommender Systems Movie. Lens Firefly Movie. Critic

Eigen. Taste Algorithm 1) Principal Component Analysis 2) Universal Queries (dense ratings matrix) 3) Fine-grained ratings bar (captures nuances) 4) Offline and Online Processing 5) Online: Constant time recommendations

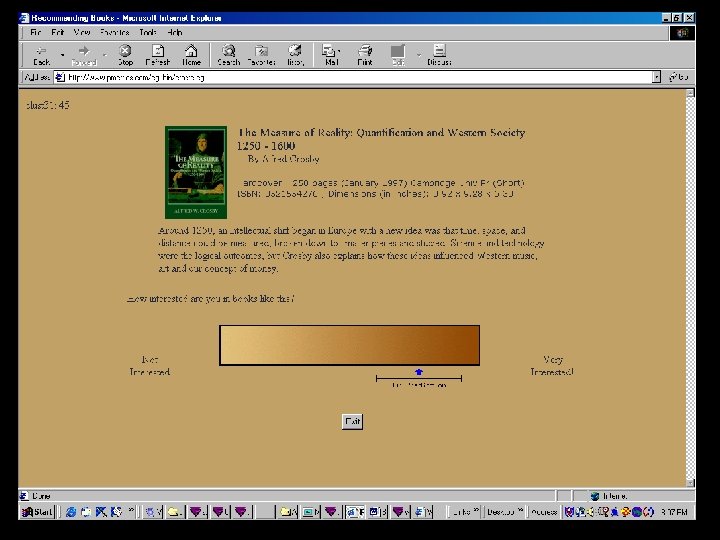
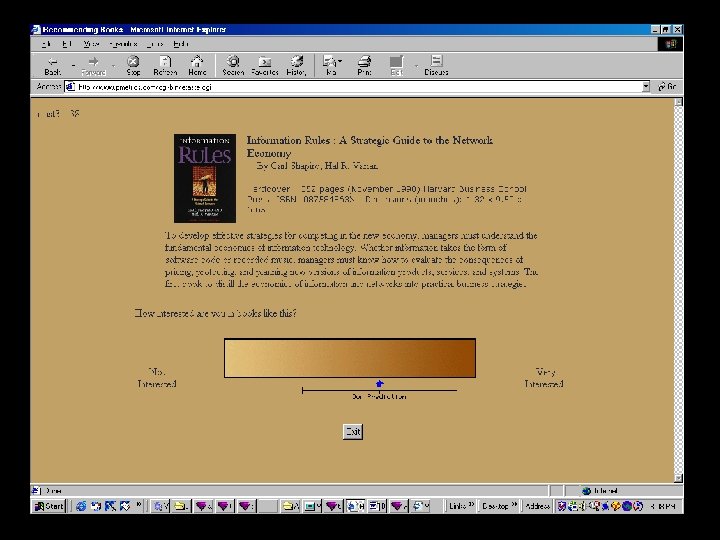
Universal Queries • Most CF systems require users to select which items they want to rate: sparse ratings matrix • Eigentaste allows users to rate all items based on short unbiased descriptions (eg, film synopsis) • Eigentaste uses a subset of highly discriminatory items for the gauge set

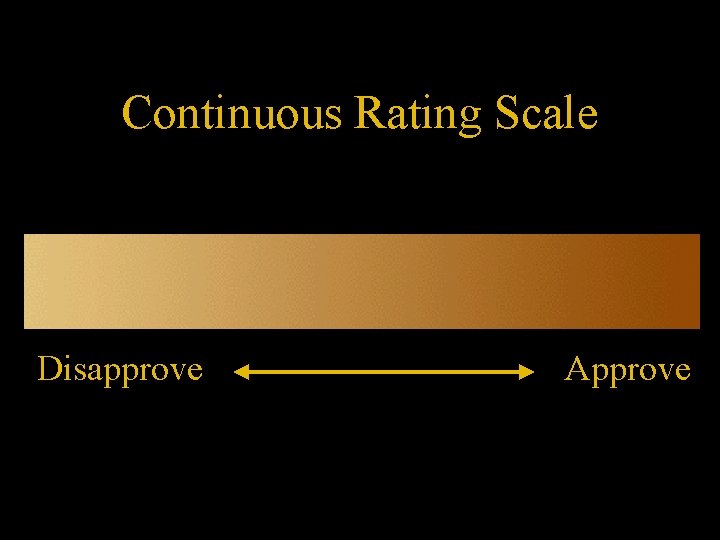
Continuous Rating Scale Disapprove Approve

Eigen. Taste Algorithm • A is the n x m normalized rating matrix – n users – m objects • C is the k x k reduced correlation matrix – k objects in the gauge set: – C = (1/n) ATA – assumes ratings are continuous with linear rel. • E is the ortho. matrix of eigenvectors of C • is the diagonal matrix of eigenvalues

Correlation Matrix

Eigen. Taste • • ECET = C = ET E Let B = AET RB = (1/n) BTB = ECET = – transformed points are uncorrelated and each column of B has variance i • Principle Components (Pearson 1901) – consider m largest eigenvectors, Em • Bm = AEm. T • choose m based on “knee” in eigenvalues

Dimensionality Reduction • First two principal components (eigenvectors) account for nearly 50% of the variation in user ratings • Project user ratings along first two principal components: x = AE 2 T • Facilitates visualization. . .

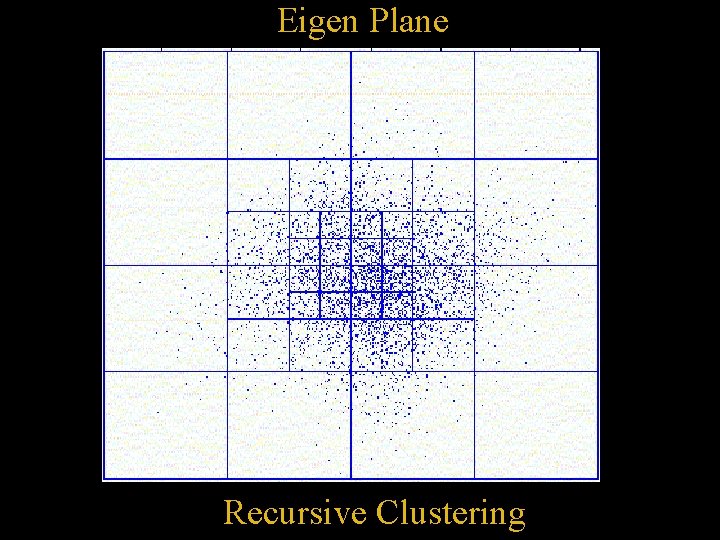
Eigen Plane Recursive Clustering

The Eigen. Taste Algorithm • Offline: – Compute eigenvectors and project users onto eigen plane. – Cluster and compute average ratings for each cluster. • Online: – Collect ratings for objects in gauge set – Project onto the eigen plane – Find representative cluster – Recommend objects based on average ratings within that cluster

First Application (1999) Jester: Recommending Jokes • Sense of humor is difficult to specify • Advantages: – Rating process is not altogether unpleasant – Can evaluate jokes quickly: – Dense ratings matrix (large sample size) • Disadvantages: – Offensive/Shaggy Dog jokes – Temporal Effects, Portfolio Effects – Priming/Masking

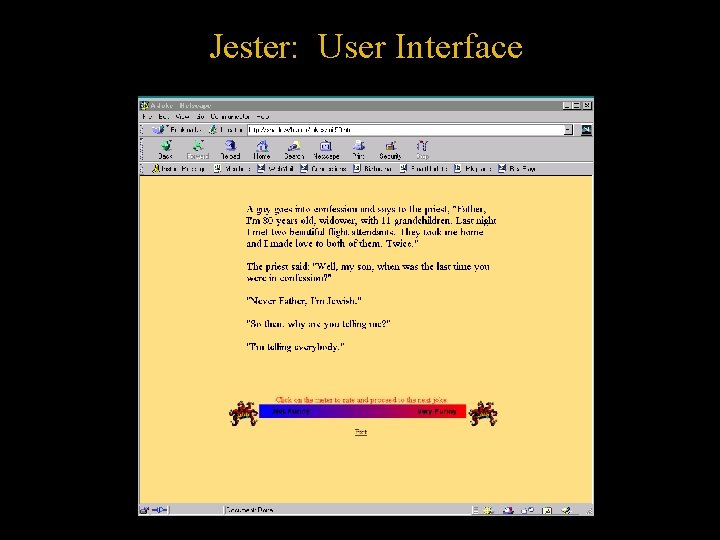
Jester: User Interface

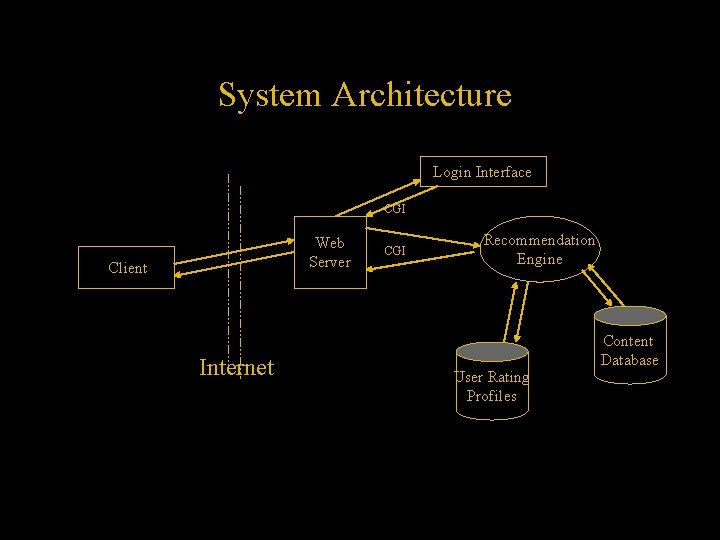
System Architecture Login Interface CGI Web Server Client Internet CGI Recommendation Engine User Rating Profiles Content Database

Measure of Effectiveness Metric: Normalized Mean Absolute Error (NMAE): Average absolute deviation of actual ratings from predicted ratings, normalized over rating range. MAE = 1/c |r - p| NMAE = MAE / (r_max - r_min)

Effectiveness Based on 18, 000 users

Computational Complexity n - number of users k - number of objects in gauge set Nearest Neighborhood algorithm : Online processing - O(kn) Eigen. Taste algorithm: Offline processing - O(k 2 n) Online processing - O(k)

Effectiveness and Efficiency

Prediction Speed Algorithm Nearest Neighbor Eigen. Taste Time to process 9000 users 28 hours 3 minutes

Current Jester Dataset 62, 000 registered users approx. 3, 000 ratings

Second Application (2000) Sleeper: Recommending Books

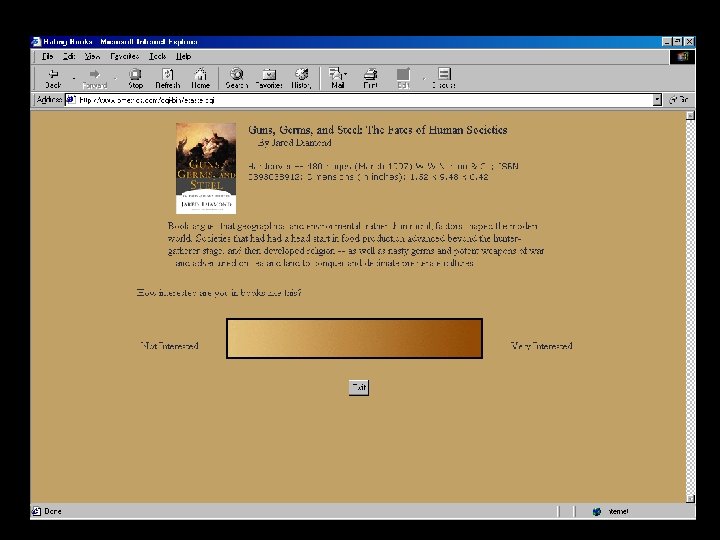
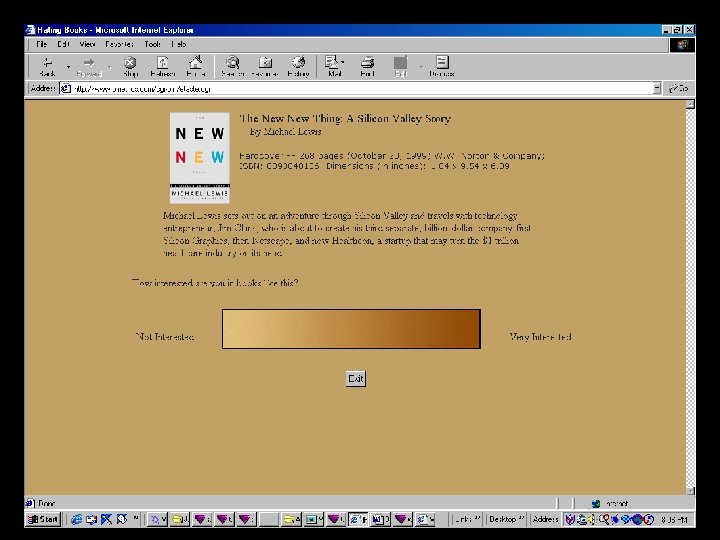
Eigen. Taste Algorithm 1) Principal Component Analysis 2) Universal Queries (dense ratings matrix) 3) Fine-grained ratings bar (captures nuances) 4) Offline and Online Processing 5) Online: Constant time recommendations Patent application 21 December 1999 by UC Regents

www. cs. berkeley. edu/~goldberg@cs. berkeley. edu Eigentaste: A Constant Time Collaborative Filtering Algorithm (to appear: Information Retrieval Journal, 2001)